बिग डेटा एनालिटिक्स - टाइम सीरीज विश्लेषण
टाइम सीरीज़ एक तिथि या टाइमस्टैम्प द्वारा अनुक्रमित श्रेणीबद्ध या संख्यात्मक चर की टिप्पणियों का एक अनुक्रम है। समय श्रृंखला डेटा का एक स्पष्ट उदाहरण स्टॉक मूल्य का समय श्रृंखला है। निम्न तालिका में, हम समय श्रृंखला डेटा की बुनियादी संरचना देख सकते हैं। इस मामले में हर घंटे अवलोकन दर्ज किए जाते हैं।
| समय-चिह्न | शेयर की कीमत |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
आम तौर पर, समय श्रृंखला विश्लेषण में पहला कदम श्रृंखला की साजिश है, यह आम तौर पर एक लाइन चार्ट के साथ किया जाता है।
समय श्रृंखला विश्लेषण का सबसे आम अनुप्रयोग डेटा के अस्थायी ढांचे का उपयोग करके एक संख्यात्मक मूल्य के भविष्य के मूल्यों का पूर्वानुमान है। इसका मतलब है, उपलब्ध टिप्पणियों का उपयोग भविष्य से मूल्यों की भविष्यवाणी करने के लिए किया जाता है।
डेटा के अस्थायी आदेश का तात्पर्य है कि पारंपरिक प्रतिगमन विधियाँ उपयोगी नहीं हैं। मजबूत पूर्वानुमान बनाने के लिए, हमें उन मॉडलों की आवश्यकता होती है जो डेटा के अस्थायी आदेश को ध्यान में रखते हैं।
टाइम सीरीज़ विश्लेषण के लिए सबसे व्यापक रूप से इस्तेमाल किया जाने वाला मॉडल कहा जाता है Autoregressive Moving Average(ARMA)। मॉडल में दो भाग होते हैं, aautoregressive (एआर) भाग और ए moving average(एमए) भाग। मॉडल को आमतौर पर ARMA (p, q) मॉडल के रूप में संदर्भित किया जाता है जहां p ऑटोर्रिजेक्टिव भाग का क्रम है और q चलती औसत भाग का क्रम है।
ऑटोरेग्रेसिव मॉडल
एआर (पी) के क्रम पी के एक autoregressive मॉडल के रूप में पढ़ा जाता है। गणितीय रूप से इसे इस प्रकार लिखा जाता है -
$ $ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $ $
जहाँ { are 1 ,…, } p } अनुमानित किए जाने वाले पैरामीटर हैं, c एक स्थिर है, और यादृच्छिक चर noise t सफेद शोर का प्रतिनिधित्व करता है। कुछ अवरोध मापदंडों के मूल्यों पर आवश्यक हैं ताकि मॉडल स्थिर रहे।
सामान्य गति
अंकन एमए (q) क्रम q के मूविंग औसत मॉडल को संदर्भित करता है -
$ $ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
जहां θ 1 , ..., θ क्ष मॉडल के मापदंडों हैं, μ एक्स की उम्मीद है टी , और ε टी , ε टी - 1 , ..., सफेद शोर त्रुटि शब्द हैं।
ऑटोरेग्रेसिव मूविंग एवरेज
ARMA (पी, क्यू) मॉडल को जोड़ती है पी autoregressive नियम और क्ष चलती-औसत शर्तों। गणितीय रूप से मॉडल निम्नलिखित सूत्र के साथ व्यक्त किया गया है -
$ $ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ ata_i \ varepsilon_ {ti} $ $
हम देख सकते हैं कि ARMA (p, q) मॉडल AR (p) और MA (q) मॉडल का संयोजन है ।
मॉडल के कुछ अंतर्ज्ञान देने के लिए विचार है कि समीकरण के एआर हिस्सा एक्स के लिए मानकों को अनुमान लगाने के लिए करना चाहता है टी - मैं आदेश एक्स में चर के मूल्य की भविष्यवाणी करने में की टिप्पणियों टी । यह अंत में पिछले मूल्यों का एक भारित औसत है। एमए खंड समान दृष्टिकोण का उपयोग करता है लेकिन पिछली टिप्पणियों की त्रुटि के साथ, i t - i । तो अंत में, मॉडल का परिणाम एक भारित औसत है।
निम्नलिखित कोड स्निपेट दर्शाता है कि आर में एआरएमए (पी, क्यू) कैसे लागू किया जाए ।
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)डेटा को प्लॉट करना आम तौर पर यह पता लगाने के लिए पहला कदम है कि क्या डेटा में एक अस्थायी संरचना है। हम साजिश से देख सकते हैं कि प्रत्येक वर्ष के अंत में मजबूत स्पाइक्स हैं।
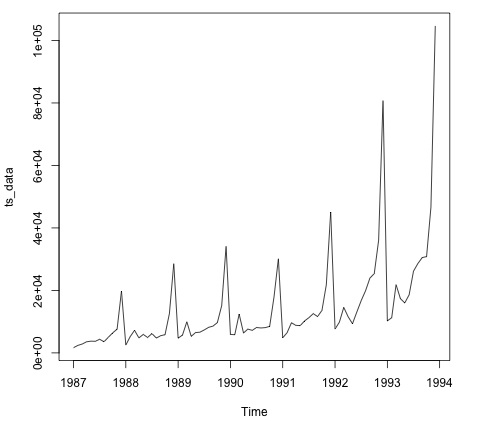
निम्न कोड डेटा के लिए एक ARMA मॉडल फिट बैठता है। यह मॉडल के कई संयोजन चलाता है और कम त्रुटि वाले का चयन करता है।
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172