कंपाइलर डिज़ाइन - टॉप-डाउन पार्सर
हमने पिछले अध्याय में सीखा है कि टॉप-डाउन पार्सिंग तकनीक इनपुट को पार्स करती है, और रूट नोड से एक पार्स ट्री का निर्माण शुरू करती है जो धीरे-धीरे पत्ती नोड्स तक नीचे जाती है। ऊपर-नीचे पार्सिंग के प्रकारों को नीचे दर्शाया गया है:
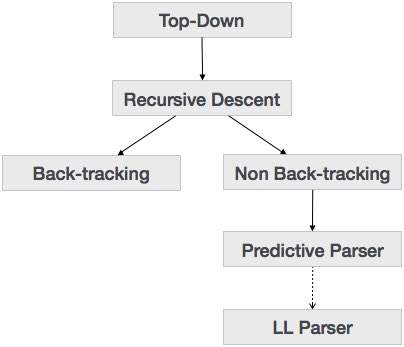
पुनरावर्ती वंश परासन
रिकर्सिव डिसेंट एक टॉप-डाउन पार्सिंग तकनीक है जो ऊपर से पार्स ट्री का निर्माण करती है और इनपुट को बाएं से दाएं पढ़ा जाता है। यह हर टर्मिनल और गैर-टर्मिनल इकाई के लिए प्रक्रियाओं का उपयोग करता है। यह पार्सिंग तकनीक पुन: पार्स ट्री बनाने के लिए इनपुट को पार्स करती है, जिसे बैक-ट्रैकिंग की आवश्यकता हो सकती है या नहीं। लेकिन इससे जुड़ा व्याकरण (यदि तथ्य नहीं छोड़ा गया तो) बैक-ट्रैकिंग से नहीं बच सकता। पुनरावर्ती-वंशीय पार्सिंग का एक रूप जिसे किसी भी बैक-ट्रैकिंग की आवश्यकता नहीं होती है, के रूप में जाना जाता हैpredictive parsing।
पार्सिंग तकनीक को पुनरावर्ती माना जाता है क्योंकि यह संदर्भ-मुक्त व्याकरण का उपयोग करता है जो प्रकृति में पुनरावर्ती है।
वापस ट्रैकिंग
टॉप-डाउन पार्सर रूट नोड (स्टार्ट सिंबल) से शुरू होते हैं और उन्हें बदलने के लिए उत्पादन नियमों के खिलाफ इनपुट स्ट्रिंग से मिलान करते हैं (यदि मिलान किया जाता है)। इसे समझने के लिए, CFG का निम्नलिखित उदाहरण लें:
S → rXd | rZd
X → oa | ea
Z → aiएक इनपुट स्ट्रिंग के लिए: पढ़ें, एक टॉप-डाउन पार्सर, इस तरह से व्यवहार करेगा:
यह उत्पादन नियमों से S से शुरू होगा और इनपुट के बाएं-सबसे अक्षर यानी 'r' से इसकी उपज का मिलान करेगा। एस (एस → आरएक्सडी) का बहुत उत्पादन इसके साथ मेल खाता है। तो अगले इनपुट पत्र (यानी 'ई') के लिए ऊपर-नीचे पार्सर अग्रिम। पार्सर गैर-टर्मिनल 'एक्स' का विस्तार करने की कोशिश करता है और बाईं ओर (एक्स → ओए) से इसके उत्पादन की जांच करता है। यह अगले इनपुट प्रतीक के साथ मेल नहीं खाता है। तो एक्स के अगले उत्पादन नियम, (एक्स → ईआर) को प्राप्त करने के लिए टॉप-डाउन पार्सर बैकट्रैक।
अब पार्सर सभी इनपुट अक्षरों को एक क्रमबद्ध तरीके से मिलाता है। स्ट्रिंग को स्वीकार किया जाता है।
|
|
|
|
|
भविष्य कहनेवाला
प्रिडिक्टिव पार्सर एक पुनरावर्ती डीसेंट पार्सर है, जिसमें यह अनुमान लगाने की क्षमता है कि इनपुट स्ट्रिंग को बदलने के लिए किस उत्पादन का उपयोग किया जाना है। भविष्य कहनेवाला पार्सर बैकट्रैकिंग से ग्रस्त नहीं है।
अपने कार्यों को पूरा करने के लिए, भविष्य कहनेवाला पार्सर एक लुक-फॉरवर्ड पॉइंटर का उपयोग करता है, जो अगले इनपुट प्रतीकों की ओर इशारा करता है। पार्सर को बैक-ट्रैकिंग मुक्त बनाने के लिए, भविष्य कहनेवाला पार्सर व्याकरण पर कुछ अड़चन डालता है और केवल व्याकरण के एक वर्ग को एलएल (के) व्याकरण के रूप में जाना जाता है।
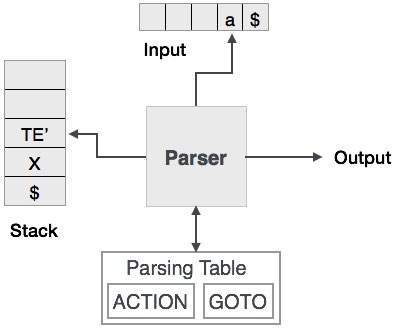
प्रिडिक्टिव पर्सिंग इनपुट को पार्स करने और पार्स ट्री जनरेट करने के लिए स्टैक और पार्सिंग टेबल का उपयोग करता है। स्टैक और इनपुट दोनों में एक अंतिम प्रतीक होता है$यह बताने के लिए कि स्टैक खाली है और इनपुट का उपभोग किया जाता है। पार्सर इनपुट और स्टैक तत्व संयोजन पर कोई निर्णय लेने के लिए पार्सिंग टेबल को संदर्भित करता है।
पुनरावर्ती वंशीय पार्सिंग में, पार्सर के पास इनपुट के एक ही उदाहरण के लिए चुनने के लिए एक से अधिक उत्पादन हो सकते हैं, जबकि भविष्य कहनेवाला पार्सर में, चुनने के लिए प्रत्येक चरण में अधिकतम एक उत्पादन होता है। ऐसे उदाहरण हो सकते हैं जहां इनपुट स्ट्रिंग से मेल खाते कोई उत्पादन नहीं है, जिससे पार्सिंग प्रक्रिया विफल हो जाती है।
एलएल पार्सर
एक LL पार्सर LL व्याकरण को स्वीकार करता है। LL व्याकरण संदर्भ-मुक्त व्याकरण का एक सबसेट है, लेकिन सरल कार्यान्वयन प्राप्त करने के लिए सरलीकृत संस्करण प्राप्त करने के लिए कुछ प्रतिबंधों के साथ। LL व्याकरण दोनों एल्गोरिदम अर्थात् पुनरावर्ती-वंश या तालिका-चालित के माध्यम से कार्यान्वित किया जा सकता है।
LL पार्सर को LL (k) के रूप में निरूपित किया जाता है। एलएल (के) में पहला एल बाएं से दाएं इनपुट को पार्स कर रहा है, एलएल (के) में दूसरा एल बाईं ओर सबसे अधिक व्युत्पत्ति के लिए खड़ा है और के खुद लुक की संख्या का प्रतिनिधित्व करता है। आम तौर पर k = 1, इसलिए LL (k) को LL (1) के रूप में भी लिखा जा सकता है।
एलएल पार्सिंग एल्गोरिथम
हम पार्सर स्पष्टीकरण के लिए निर्धारक एलएल (1) से चिपक सकते हैं, क्योंकि तालिका का आकार कश्मीर के मूल्य के साथ तेजी से बढ़ता है। दूसरे, यदि कोई दिया गया व्याकरण LL (1) नहीं है, तो आमतौर पर, यह किसी दिए गए k के लिए LL (k) नहीं है।
नीचे एलएल (1) पार्सिंग के लिए एक एल्गोरिदम दिया गया है:
Input:
string ω
parsing table M for grammar G
Output:
If ω is in L(G) then left-most derivation of ω,
error otherwise.
Initial State : $S on stack (with S being start symbol)
ω$ in the input buffer
SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ Vt or $
if X = a
POP X and advance ip.
else
error()
endif
else /* X is non-terminal */
if M[X,a] = X → Y1, Y2,... Yk
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
Output the production X → Y1, Y2,... Yk
else
error()
endif
endif
until X = $ /* empty stack */एक व्याकरण G, LL (1) है यदि A → α | जी के दो अलग-अलग निर्माण हैं:
कोई टर्मिनल के लिए, दोनों α और ive व्युत्पन्न तार एक के साथ शुरुआत।
α और at में से एक पर खाली स्ट्रिंग प्राप्त कर सकते हैं।
यदि ive → t, तो α FOLLOW (A) में टर्मिनल के साथ कोई स्ट्रिंग शुरुआत नहीं करता है।