कंप्यूटर ग्राफिक्स घटता है
कंप्यूटर ग्राफिक्स में, हमें अक्सर स्क्रीन पर विभिन्न प्रकार की वस्तुओं को खींचने की आवश्यकता होती है। ऑब्जेक्ट्स हर समय सपाट नहीं होते हैं और हमें ऑब्जेक्ट खींचने के लिए कई बार कर्व्स खींचने होते हैं।
घटता प्रकार
एक वक्र एक असीम रूप से बड़े बिंदुओं का समूह है। प्रत्येक बिंदु में समापन बिंदु को छोड़कर दो पड़ोसी हैं। घटता को मोटे तौर पर तीन श्रेणियों में वर्गीकृत किया जा सकता है -explicit, implicit, तथा parametric curves।
इम्प्लिक्ट कर्व्स
इम्प्लिक्ट कर्व रिप्रेजेंटेशन एक वक्र को नियोजित करके एक वक्र पर बिंदुओं के सेट को परिभाषित करता है जो यह देखने के लिए परीक्षण कर सकता है कि क्या वक्र पर कोई बिंदु है। आमतौर पर, एक निहित वक्र को रूप के एक निहित कार्य द्वारा परिभाषित किया जाता है -
f (x, y) = 0
यह बहुस्तरीय घटता (एक x मान के लिए कई y मान) का प्रतिनिधित्व कर सकता है। एक सामान्य उदाहरण सर्कल है, जिसका निहित प्रतिनिधित्व है
x2 + y2 - R2 = 0
स्पष्ट वक्र
एक गणितीय फ़ंक्शन y = f (x) को वक्र के रूप में प्लॉट किया जा सकता है। इस तरह के एक फ़ंक्शन वक्र का स्पष्ट प्रतिनिधित्व है। स्पष्ट प्रतिनिधित्व सामान्य नहीं है, क्योंकि यह ऊर्ध्वाधर लाइनों का प्रतिनिधित्व नहीं कर सकता है और एकल-मूल्यवान भी है। X के प्रत्येक मान के लिए, y का केवल एक मान सामान्य रूप से फ़ंक्शन द्वारा गणना किया जाता है।
पैरामीट्रिक वक्र
पैरामीट्रिक फॉर्म वाले वक्रों को पैरामीट्रिक वक्र कहा जाता है। फ़ंक्शन ज्ञात होने पर ही स्पष्ट और अंतर्निहित वक्र अभ्यावेदन का उपयोग किया जा सकता है। व्यवहार में पैरामीट्रिक घटता का उपयोग किया जाता है। द्वि-आयामी पैरामीट्रिक वक्र का निम्न रूप है -
पी (टी) = एफ (टी), जी (टी) या पी (टी) = एक्स (टी), वाई (टी)
फ़ंक्शंस और जी बन जाते हैं (एक्स, वाई) वक्र पर किसी बिंदु के निर्देशांक, और अंक प्राप्त होते हैं जब पैरामीटर टी एक निश्चित अंतराल पर भिन्न होता है [ए, बी], सामान्य रूप से [0, 1]।
बेज़ियर कर्व्स
बेज़ियर वक्र की खोज फ्रांसीसी इंजीनियर ने की है Pierre Bézier। इन वक्रों को अन्य बिंदुओं के नियंत्रण में उत्पन्न किया जा सकता है। नियंत्रण बिंदु का उपयोग करके अनुमानित स्पर्शरेखा का उपयोग वक्र उत्पन्न करने के लिए किया जाता है। बेजियर वक्र का गणितीय रूप से प्रतिनिधित्व किया जा सकता है -
$$ \ sum_ {k = 0} ^ {n} P_ {i} {B_ {i} ^ {n}} (t) $$
जहाँ $ p_ {i} $ बिंदुओं का समुच्चय है और $ {B_ {i} ^ {n}} (t) $ बर्नस्टीन बहुपद का प्रतिनिधित्व करता है जो इसके द्वारा दिए गए हैं -
$ $ {B_ {i} ^ {n}} (t) = \ binom {n} {i} (1 - t) ^ {ni} t ^ {i} $ $
कहाँ पे n बहुपद डिग्री है, i सूचकांक है, और t परिवर्तनशील है।
सबसे सरल Bézier वक्र बिंदु $ P_ {0} $ से $ P_ {1} $ की सीधी रेखा है। एक द्विघाती बेज़ियर वक्र तीन नियंत्रण बिंदुओं द्वारा निर्धारित किया जाता है। एक क्यूबिक बेजियर वक्र चार नियंत्रण बिंदुओं द्वारा निर्धारित किया जाता है।
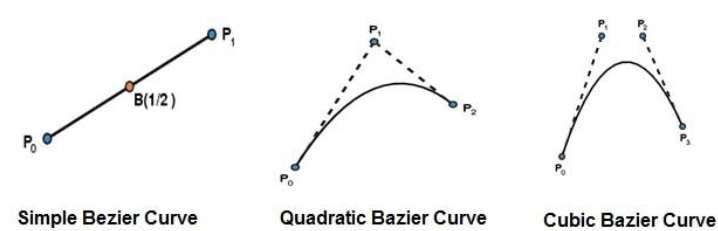
बेज़ियर कर्व्स के गुण
बेजियर घटता में निम्नलिखित गुण हैं -
वे आम तौर पर नियंत्रण बहुभुज के आकार का पालन करते हैं, जिसमें नियंत्रण बिंदुओं से जुड़ने वाले खंड शामिल होते हैं।
वे हमेशा पहले और आखिरी नियंत्रण बिंदु से गुजरते हैं।
वे अपने परिभाषित नियंत्रण बिंदुओं के उत्तल पतवार में निहित हैं।
वक्र खंड को परिभाषित करने वाले बहुपद की डिग्री एक कम है जो बहुभुज बिंदु को परिभाषित करने की संख्या है। इसलिए, 4 नियंत्रण बिंदुओं के लिए, बहुपद की डिग्री 3 है, यानी घन बहुपद।
एक बेजियर वक्र आम तौर पर परिभाषित बहुभुज के आकार का अनुसरण करता है।
अंत बिंदुओं पर स्पर्शरेखा वेक्टर की दिशा पहले और अंतिम खंडों द्वारा निर्धारित वेक्टर के समान है।
बेज़ियर वक्र के लिए उत्तल पतवार संपत्ति सुनिश्चित करती है कि बहुपद आसानी से नियंत्रण बिंदुओं का अनुसरण करता है।
कोई भी सीधी रेखा एक बेज़ियर वक्र को अधिक बार नहीं काटती है, क्योंकि यह अपने नियंत्रण बहुभुज को काटता है।
वे एक परिवर्तन के तहत अपरिवर्तनीय हैं।
बेज़ियर घटता वैश्विक नियंत्रण का मतलब है कि एक नियंत्रण बिंदु हिलना पूरे वक्र के आकार को बदल देता है।
एक दिया हुआ बेज़ियर वक्र दो बेज़ियर सेगमेंट में एक बिंदु t = t0 पर उप-विभाजित किया जा सकता है, जो पैरामीटर मान t = t0 के अनुरूप बिंदु पर एक साथ जुड़ता है।
बी-स्पाइन कर्व्स
बर्नस्टीन आधार समारोह द्वारा उत्पादित बेजियर-वक्र में सीमित लचीलापन है।
सबसे पहले, निर्दिष्ट बहुभुज कोने की संख्या परिणामी बहुपद के क्रम को ठीक करती है जो वक्र को परिभाषित करती है।
दूसरी सीमित विशेषता यह है कि सम्मिश्रण फ़ंक्शन का मान पूरे वक्र पर सभी पैरामीटर मानों के लिए नॉनज़रो है।
बी-स्पलाइन आधार में विशेष मामले के रूप में बर्नस्टीन आधार शामिल है। बी-स्पलाइन आधार गैर-वैश्विक है।
बी-स्पाइन वक्र को नियंत्रण बिंदु पाई और बी-स्पलाइन आधार फ़ंक्शन $ N_ {i,} $ k (t) द्वारा रेखीय संयोजन के रूप में परिभाषित किया गया है
$ C (t) = \ sum_ {i = 0} ^ {n} P_ {i} N_ {i, k} (t), $ $ n \ geq k-1, $ $ t \: \ epsilon \: [ tk-1, tn + 1] $
कहाँ पे,
{$ p_ {i} $: i = 0, 1, 2… .n} नियंत्रण बिंदु हैं
k बी-स्पाइन वक्र के बहुपद खंडों का क्रम है। आदेश k का अर्थ है कि वक्र डिग्री k - 1 के टुकड़े के बहुपद खंडों से बना है।
$ N_ {i, k} (t) $ "सामान्यीकृत बी-स्पलाइन सम्मिश्रण कार्य" हैं। वे क्रम k द्वारा वर्णित हैं और वास्तविक संख्याओं के एक गैर-घटते अनुक्रम द्वारा जिन्हें आम तौर पर "गाँठ अनुक्रम" कहा जाता है।
$ $ {t_ {i}: i = 0, ... n + K} $ $
N i , k फ़ंक्शन निम्नानुसार वर्णित हैं -
$ $ N_ {i, 1} (t) = \ left \ {\ {start {मैट्रिक्स} 1, और if \: u \: \ epsilon \: [t_ {i,} t_ {i + 1}) \\ 0 , और अन्यथा \ end {मैट्रिक्स} \ right। $ $
और अगर k> 1,
$$ N_ {i, k} (t) = \ frac {t-t_ {i}} {t_ {i + k-1}} N_ {i, k-1} (t) + \ frac {t_ {i + k} -t} {t_ {i + k} - t_ {i + 1}} N_ {i + 1, k-1} (t) $$
तथा
$ $ t \: \ epsilon \: [t_ {k-1}, t_ {n + १}} $ $
बी-स्पाइन कर्व के गुण
बी-स्पाइन घटता में निम्नलिखित गुण हैं -
किसी भी पैरामीटर मान के लिए बी-स्पलाइन आधार फ़ंक्शन का योग 1 है।
प्रत्येक आधार फ़ंक्शन सभी पैरामीटर मानों के लिए सकारात्मक या शून्य है।
प्रत्येक आधार फ़ंक्शन में k = 1 को छोड़कर ठीक एक अधिकतम मूल्य है।
वक्र का अधिकतम क्रम बहुभुज को परिभाषित करने के कोने की संख्या के बराबर है।
बहुभुज को परिभाषित करने के कोने की संख्या पर बी-स्पीन बहुपद की डिग्री स्वतंत्र है।
बी-स्पलाइन स्थानीय सतह को वक्र सतह पर नियंत्रित करने की अनुमति देती है क्योंकि प्रत्येक शीर्ष पर केवल पैरामीटर मानों की एक सीमा से अधिक वक्र का आकार प्रभावित होता है जहां इसका संबद्ध आधार कार्य नॉनजरो होता है।
वक्र घटता हुआ गुण प्रदर्शित करता है।
वक्र आमतौर पर बहुभुज को परिभाषित करने के आकार का अनुसरण करता है।
पॉलीगोन को परिभाषित करने के कोने पर लागू करके किसी भी परिशोधन परिवर्तन को वक्र पर लागू किया जा सकता है।
अपने परिभाषित बहुभुज के उत्तल पतवार के भीतर वक्र रेखा।