कंप्यूटर ग्राफिक्स भग्न
एक फ्रांसीसी / अमेरिकी गणितज्ञ डॉ। बेनोइट मैंडेलब्रोट ने फ्रैक्टल्स की खोज की। फ्रैक्टल शब्द लैटिन भाषा के फ्रैक्टस शब्द से लिया गया है जिसका अर्थ है टूटा हुआ।
फ्रैक्टल्स क्या हैं?
फ्रैक्टल एक कंप्यूटर से एक ही फॉर्मूले से उत्पन्न होने वाली बहुत ही जटिल तस्वीरें हैं। वे पुनरावृत्तियों का उपयोग करके बनाए गए हैं। इसका मतलब है कि एक सूत्र को बार-बार अलग-अलग मूल्यों के साथ दोहराया जाता है, पिछले पुनरावृत्ति से परिणामों को ध्यान में रखता है।
कई क्षेत्रों में भग्न का उपयोग किया जाता है जैसे -
Astronomy - आकाशगंगाओं, शनि के छल्लों आदि का विश्लेषण करने के लिए।
Biology/Chemistry - बैक्टीरिया संस्कृतियों, रासायनिक प्रतिक्रियाओं, मानव शरीर रचना, अणुओं, पौधों को चित्रित करने के लिए,
Others - बादलों, तटरेखा और सीमा रेखा, डेटा संपीड़न, प्रसार, अर्थव्यवस्था, भग्न कला, भग्न संगीत, परिदृश्य, विशेष प्रभाव, आदि के चित्रण के लिए।

फ्रैक्टल्स का निर्माण
निम्नलिखित आकृति में दिखाए गए अनुसार बार-बार एक ही आकार को दोहराते हुए भग्न उत्पन्न हो सकते हैं। आकृति में (ए) एक समबाहु त्रिभुज को दर्शाता है। आकृति (b) में, हम देख सकते हैं कि त्रिभुज को स्टार जैसी आकृति बनाने के लिए दोहराया जाता है। आकृति (c) में, हम देख सकते हैं कि आकृति (b) में तारा आकार फिर से दोहराया गया है और एक नया आकार बना रहा है।
हम वांछित आकार बनाने के लिए असीमित संख्या में पुनरावृत्ति कर सकते हैं। प्रोग्रामिंग शब्दों में, इस तरह के आकार बनाने के लिए पुनरावृत्ति का उपयोग किया जाता है।

ज्यामितीय भग्न
ज्यामितीय भग्न प्रकृति में पाए जाने वाले आकृतियों से निपटते हैं जिनमें गैर-पूर्णांक या भग्न आयाम होते हैं। ज्यामितीय रूप से एक नियतात्मक (गैर-आयामी) स्व-समान भग्न का निर्माण करने के लिए, हम एक दिए गए ज्यामितीय आकार के साथ शुरू करते हैं, जिसे आकार कहा जाता हैinitiator। सर्जक के उपसर्गों को एक पैटर्न के साथ बदल दिया जाता है, जिसे कहा जाता हैgenerator।

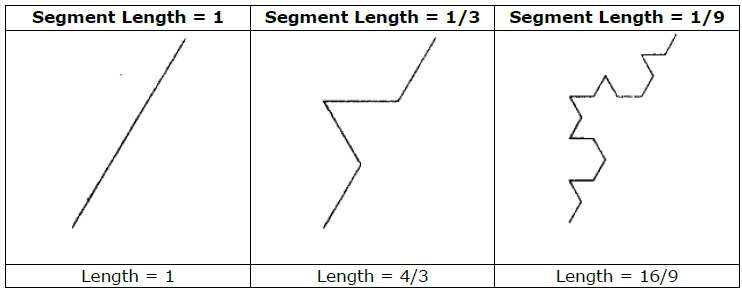
एक उदाहरण के रूप में, यदि हम उपरोक्त चित्र में दिखाए गए सर्जक और जनरेटर का उपयोग करते हैं, तो हम इसे दोहराकर अच्छे पैटर्न का निर्माण कर सकते हैं। सर्जक में प्रत्येक स्ट्रेट-लाइन सेगमेंट को प्रत्येक चरण पर चार समान-लंबाई लाइन सेगमेंट के साथ बदल दिया जाता है। स्केलिंग कारक 1/3 है, इसलिए भग्न आयाम डी = एलएन 4 / एलएन 3 ≈ 1.2619 है।
इसके अलावा, सर्जक में प्रत्येक लाइन सेगमेंट की लंबाई प्रत्येक चरण में 4/3 के कारक से बढ़ जाती है, जिससे कि फ्रैक्टल वक्र की लंबाई अनंत हो जाती है क्योंकि निम्न आकृति में दिखाए अनुसार वक्र को और अधिक विस्तार से जोड़ा जाता है -