त्वरित गाइड
किसी भी मात्रा को मापने के लिए उपयोग किए जाने वाले उपकरणों को माप उपकरणों के रूप में जाना जाता है। यह ट्यूटोरियल मुख्य रूप से शामिल हैelectronic instruments, जो या तो बिजली की मात्रा या मापदंडों को मापने के लिए उपयोगी हैं।
निम्नलिखित सबसे अधिक उपयोग किए जाने वाले इलेक्ट्रॉनिक उपकरण हैं।
- Voltmeter
- Ammeter
- Ohmmeter
- Multimeter
अब, हम इन उपकरणों के बारे में संक्षेप में चर्चा करते हैं।
वाल्टमीटर
जैसा कि नाम सुझाव देता है, voltmeterएक मापक यंत्र है जो किसी विद्युत परिपथ के दो बिंदुओं पर वोल्टेज को मापता है। दो प्रकार के वोल्टमीटर होते हैं: डीसी वाल्टमीटर, और एसी वोल्टमीटर।
डीसी वोल्टमीटर किसी विद्युत परिपथ के दो बिंदुओं में DC वोल्टेज को मापता है, जबकि AC वोल्टमीटर किसी विद्युत परिपथ के किसी भी दो बिंदुओं पर AC वोल्टेज को मापता है। का एक उदाहरणpractical DC voltmeter नीचे दिए गए आंकड़े में दिखाया गया है।

उपरोक्त आकृति में दिखाया गया डीसी वाल्टमीटर एक है $(0-100)V$ DC voltmeter। इसलिए, इसका उपयोग शून्य वोल्ट से 10 वोल्ट तक डीसी वोल्टेज को मापने के लिए किया जा सकता है।
एम्मिटर
जैसा कि नाम सुझाव देता है, ammeterएक मापने वाला उपकरण है जो विद्युत सर्किट के किसी भी दो बिंदुओं के माध्यम से बहने वाले वर्तमान को मापता है। दो प्रकार के एमीटर हैं: डीसी एमीटर, और एसी एमीटर।
डीसी एम्मीटर डीसी करंट को मापता है जो किसी विद्युत परिपथ के दो बिंदुओं से होकर बहता है। जबकि, एसी एमीटर बिजली के सर्किट के किसी भी दो बिंदुओं से बहने वाले एसी करंट को मापता है। का एक उदाहरणpractical AC ammeter नीचे चित्र में दिखाया गया है -

उपरोक्त आकृति में दिखाया गया एसी एमीटर एक है $(0-100)A \:$ AC ammeter। इसलिए, इसका उपयोग शून्य धाराओं से 100 एम्पीयर तक एसी धाराओं को मापने के लिए किया जा सकता है।
ohmmeter
Ohmmeterविद्युत परिपथ के किसी भी दो बिंदुओं के बीच प्रतिरोध के मान को मापने के लिए प्रयोग किया जाता है। इसका उपयोग किसी अज्ञात रोकनेवाला के मूल्य को खोजने के लिए भी किया जा सकता है। ओममीटर के दो प्रकार हैं: श्रृंखला ओममीटर, और शंट ओममीटर।
श्रृंखला प्रकार ओममीटर में, रोकनेवाला जिसका मूल्य अज्ञात है और मापा जाना है, ओममीटर के साथ श्रृंखला में जुड़ा होना चाहिए। यह मापने के लिए उपयोगी हैhigh values of resistances।

शंट प्रकार ओममीटर में, रोकनेवाला जिसका मूल्य अज्ञात है और मापा जाना है, ओहियोमीटर के साथ समानांतर (शंट) में जुड़ा होना चाहिए। यह मापने के लिए उपयोगी हैlow values of resistances।
का एक उदाहरण practical shunt ohmmeterउपरोक्त आंकड़े में दिखाया गया है। ऊपर चित्र में दिखाया गया ओममीटर एक है$(0-100)\Omega$ shunt ohmmeter। इसलिए, इसका उपयोग शून्य ओम से 100 ओम तक प्रतिरोध मानों को मापने के लिए किया जा सकता है।
मल्टीमीटर
Multimeterएक इलेक्ट्रॉनिक उपकरण है जिसका उपयोग वोल्टेज, करंट और प्रतिरोध जैसी मात्राओं को मापने के लिए किया जाता है। इसका उपयोग डीसी और एसी वोल्टेज, डीसी और एसी धाराओं और कई श्रेणियों के प्रतिरोध को मापने के लिए किया जा सकता है। एक व्यावहारिक मल्टीमीटर निम्नलिखित आकृति में दिखाया गया है -

जैसा कि चित्र में दिखाया गया है, इस मल्टीमीटर का उपयोग विभिन्न उच्च प्रतिरोधों, कम प्रतिरोधों, डीसी वोल्टेज, एसी वोल्टेज, डीसी धाराओं, और एसी धाराओं को मापने के लिए किया जा सकता है। इन राशियों में से प्रत्येक के लिए विभिन्न पैमाने और मानों की सीमा उपरोक्त आकृति में अंकित है।
इस अध्याय में जिन साधनों पर हमने विचार किया है indicating type instruments, इन उपकरणों के संकेत के रूप में एक विशेष मूल्य को दर्शाते हैं और इंगित करते हैं। हम इन इलेक्ट्रॉनिक माप उपकरणों के बारे में बाद के अध्यायों में विस्तार से चर्चा करेंगे।
माप उपकरणों की विशेषताएं जो साधन के प्रदर्शन को जानने में सहायक होती हैं और किसी भी मात्रा या पैरामीटर को मापने में मदद करती हैं, के रूप में जानी जाती हैं Performance Characteristics।
प्रदर्शन विशेषताओं के प्रकार
उपकरणों की प्रदर्शन विशेषताओं को निम्नलिखित में वर्गीकृत किया जा सकता है two types।
- स्थैतिक विशेषताओं
- गतिशील विशेषताएँ
अब, इन दो प्रकारों के बारे में एक-एक करके चर्चा करते हैं।
स्थैतिक विशेषताओं
उपकरणों को मापने की मात्रा या मापदंडों की विशेषताएं do not varyसमय के संबंध में स्थिर विशेषताओं को कहा जाता है। कभी-कभी, ये मात्रा या पैरामीटर समय के संबंध में धीरे-धीरे भिन्न हो सकते हैं। निम्नलिखित की सूची हैstatic characteristics।
- Accuracy
- Precision
- Sensitivity
- Resolution
- स्थैतिक त्रुटि
अब, हम इन स्थिर विशेषताओं के बारे में एक-एक करके चर्चा करते हैं।
शुद्धता
एक उपकरण के संकेतित मूल्य के बीच बीजगणितीय अंतर, $A_{i}$ और सही मूल्य, $A_{t}$ जाना जाता है accuracy। गणितीय रूप से, इसका प्रतिनिधित्व इस प्रकार किया जा सकता है -
$$Accuracy = A_{i}- A_{t}$$
शब्द, सटीकता से संकेत मिलता है कि एक उपकरण का संकेत मूल्य कितना है, $A_{i}$ सही मूल्य के करीब है, $A_{t}$।
स्थैतिक त्रुटि
असली मूल्य के बीच का अंतर, $A_{t}$ मात्रा जो समय के संबंध में भिन्न नहीं होती है और एक साधन के संकेतित मूल्य के साथ भिन्न होती है, $A_{i}$ जाना जाता है static error, $e_{s}$। गणितीय रूप से, इसका प्रतिनिधित्व इस प्रकार किया जा सकता है -
$$e_{s}= A_{t}- A_{i}$$
शब्द, स्थिर त्रुटि साधन की अशुद्धि को दर्शाता है। यदि स्थिर त्रुटि को प्रतिशत के संदर्भ में दर्शाया जाता है, तो इसे कहा जाता हैpercentage of static error। गणितीय रूप से, इसका प्रतिनिधित्व इस प्रकार किया जा सकता है -
$$\% e_{s}=\frac{e_{s}}{A_{t}}\times 100$$
स्थानापन्न, का मान $e_{s}$ उपरोक्त समीकरण के दाहिने हाथ में -
$$\% e_{s}=\frac{A_{t}- A_{i}}{A_{t}}\times 100$$
कहाँ पे,
$\% e_{s}$ स्थिर त्रुटि का प्रतिशत है।
शुद्धता
यदि कोई साधन किसी भी संख्या में समान परिस्थितियों में समान मात्रा को मापने के लिए उपयोग किए जाने पर एक ही मूल्य को बार-बार इंगित करता है, तो हम कह सकते हैं कि साधन में उच्च है precision।
संवेदनशीलता
आउटपुट में परिवर्तन का अनुपात, $\Delta A_{out}$ इनपुट में दिए गए परिवर्तन के लिए एक उपकरण, $\Delta A_{in}$ जिसे मापा जाना है उसे कहा जाता है sensitivity, S। गणितीय रूप से इसका प्रतिनिधित्व किया जा सकता है -
$$S=\frac{\Delta A_{out}}{\Delta A_{in}}$$
संवेदनशीलता शब्द औसत दर्जे के इनपुट में सबसे छोटे परिवर्तन का संकेत देता है जो प्रतिक्रिया करने के लिए एक उपकरण के लिए आवश्यक है।
यदि अंशांकन वक्र है linear, तो साधन की संवेदनशीलता एक स्थिर होगी और यह अंशांकन वक्र के ढलान के बराबर है।
यदि अंशांकन वक्र है non-linear, तो साधन की संवेदनशीलता एक स्थिर नहीं होगी और यह इनपुट के संबंध में अलग-अलग होगी।
संकल्प
यदि किसी उपकरण का आउटपुट केवल तभी बदलेगा जब इनपुट का एक विशेष वेतन वृद्धि होगी, तो उस इनपुट का वेतन वृद्धि कहा जाता है Resolution। इसका मतलब है, इनपुट के रिज़ॉल्यूशन होने पर, उपकरण इनपुट को प्रभावी ढंग से मापने में सक्षम है।
गतिशील विशेषताएँ
उपकरणों की विशेषताएं, जिनका उपयोग मात्रा या मापदंडों को मापने के लिए किया जाता है, जो समय के संबंध में बहुत तेज़ी से भिन्न होते हैं, उन्हें गतिशील विशेषताओं कहा जाता है। निम्नलिखित की सूची हैdynamic characteristics।
- प्रतिक्रिया की गति
- गतिशील त्रुटि
- Fidelity
- Lag
अब, इन गतिशील विशेषताओं के बारे में एक-एक करके चर्चा करते हैं।
प्रतिक्रिया की गति
जब भी मापी जाने वाली मात्रा में कोई परिवर्तन होता है तो उपकरण जिस गति से प्रतिक्रिया करता है उसे कहा जाता है speed of response। यह इंगित करता है कि साधन कितना तेज है।
पीछे रह जाना
जब भी माप की जाने वाली मात्रा में कोई परिवर्तन होता है, तो एक उपकरण की प्रतिक्रिया में मौजूद विलंब की मात्रा को मापने वाला अंतराल कहा जाता है। इसे बस कहा भी जाता हैlag।
गतिशील त्रुटि
असली मूल्य के बीच का अंतर, $A_{t}$ वह मात्रा जो समय के संबंध में और एक साधन के संकेतित मूल्य के साथ बदलती है, $A_{i}$ गतिशील त्रुटि के रूप में जाना जाता है, $e_{d}$।
सत्य के प्रति निष्ठा
किसी भी गतिशील त्रुटि के बिना मापित मात्रा में परिवर्तन को इंगित करने वाला उपकरण किस हद तक जाना जाता है Fidelity
माप के दौरान होने वाली त्रुटियों को कहा जाता है measurement errors। इस अध्याय में, हम माप त्रुटियों के प्रकारों के बारे में चर्चा करते हैं।
मापन त्रुटियों के प्रकार
हम माप त्रुटियों को निम्नलिखित तीन प्रकारों में वर्गीकृत कर सकते हैं।
- सकल त्रुटियां
- रैंडम त्रुटियां
- व्यवस्थित त्रुटियां
अब, इन तीन प्रकार की माप त्रुटियों के बारे में एक-एक करके चर्चा करते हैं।
सकल त्रुटियां
माप मान लेते समय पर्यवेक्षक के अनुभव की कमी के कारण होने वाली त्रुटियों को कहा जाता है gross errors। स्थूल त्रुटियों के मूल्य पर्यवेक्षक से पर्यवेक्षक तक भिन्न होंगे। कभी-कभी, उपकरण के अनुचित चयन के कारण सकल त्रुटियां भी हो सकती हैं। हम इन दो चरणों का पालन करके सकल त्रुटियों को कम कर सकते हैं।
- मापा जाने वाले मूल्यों की सीमा के आधार पर, सबसे उपयुक्त उपकरण चुनें।
- ध्यान से रीडिंग नीचे नोट करें
व्यवस्थित त्रुटियां
यदि उपकरण एक त्रुटि पैदा करता है, जो कि इसके संचालन के दौरान एक समान वर्दी विचलन का होता है, जिसे के रूप में जाना जाता है systematic error। उपकरण में प्रयुक्त सामग्री की विशेषताओं के कारण व्यवस्थित त्रुटियां होती हैं।
Types of Systematic Errors
व्यवस्थित त्रुटियों को निम्नलिखित में वर्गीकृत किया जा सकता है three types।
Instrumental Errors - इस प्रकार की त्रुटियां उपकरणों की कमी और लोडिंग प्रभाव के कारण होती हैं।
Environmental Errors - इस प्रकार की त्रुटियां पर्यावरण में बदलाव के कारण होती हैं जैसे तापमान में परिवर्तन, दबाव और आदि।
observational Errors - मीटर रीडिंग लेते समय प्रेक्षक के कारण इस प्रकार की त्रुटियां होती हैं। Parallax errors इस प्रकार की त्रुटियों से संबंधित हैं।
रैंडम त्रुटियां
माप समय के दौरान अज्ञात स्रोतों के कारण होने वाली त्रुटियों को कहा जाता है random errors। इसलिए, इन त्रुटियों को खत्म करना या कम करना संभव नहीं है। लेकिन, अगर हम बिना किसी यादृच्छिक त्रुटि के अधिक सटीक माप मान प्राप्त करना चाहते हैं, तो यह इन दो चरणों का पालन करके संभव है।
Step1 - विभिन्न पर्यवेक्षकों द्वारा अधिक संख्या में रीडिंग लें।
Step2 - Step1 में प्राप्त रीडिंग पर सांख्यिकीय विश्लेषण करें।
निम्नलिखित पैरामीटर हैं जो सांख्यिकीय विश्लेषण में उपयोग किए जाते हैं।
- Mean
- Median
- Variance
- Deviation
- मानक विचलन
अब, इन पर चर्चा करते हैं statistical parameters।
मीन
लश्कर $x_{1},x_{2},x_{3},....,x_{N}$ हैं $N$एक विशेष माप की रीडिंग। मतलब याaverage value इन रीडिंग की गणना निम्न सूत्र का उपयोग करके की जा सकती है।
$$m = \frac{x_{1}+x_{2}+x_{3}+....+x_{N}}{N}$$
कहाँ पे, $m$ औसत या औसत मूल्य है।
यदि किसी विशेष माप के रीडिंग की संख्या अधिक है, तो औसत या औसत मूल्य लगभग बराबर होगा true value
मंझला
यदि किसी विशेष माप के रीडिंग की संख्या अधिक है, तो माध्य या औसत मूल्य की गणना करना मुश्किल है। यहां, गणना करेंmedian value और यह औसत मूल्य के बराबर होगा।
मंझला मूल्य की गणना के लिए, पहले हमें एक विशेष माप के रीडिंग को व्यवस्थित करना होगा ascending order। हम निम्न सूत्र का उपयोग करके माध्य मूल्य की गणना कर सकते हैं, जब रीडिंग की संख्या एodd number।
$$M=x_{\left ( \frac{N+1}{2} \right )}$$
हम निम्न सूत्र का उपयोग करके माध्य मूल्य की गणना कर सकते हैं, जब रीडिंग की संख्या ए even number।
$$M=\frac{x_{\left ( N/2 \right )}+x_\left ( \left [ N/2 \right ]+1 \right )}{2}$$
मतलब से विचलन
किसी विशेष माप और माध्य मान के पढ़ने के बीच के अंतर को माध्य से विचलन के रूप में जाना जाता है । संक्षेप में, इसे विचलन कहा जाता है । गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$$d_{i}=x_{i}-m$$
कहाँ पे,
$d_{i}$ का विचलन है $i^{th}$ मतलब से पढ़ना।
$x_{i}$ का मूल्य है $i^{th}$ पढ़ने।
$m$ औसत या औसत मूल्य है।
मानक विचलन
विचलन का मूल माध्य वर्ग कहलाता है standard deviation। गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$$\sigma =\sqrt{\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N}}$$
उपरोक्त सूत्र मान्य है यदि रीडिंग की संख्या, एन 20 से अधिक या उसके बराबर है। हम मानक विचलन के लिए निम्न फॉर्मूला का उपयोग कर सकते हैं, जब रीडिंग की संख्या, एन 20 से कम है।
$$\sigma =\sqrt{\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N-1}}$$
कहाँ पे,
$\sigma$ मानक विचलन है
$d_{1}, d_{2}, d_{3}, …, d_{N}$ पहले, दूसरे, तीसरे,… के विचलन हैं $N^{th}$क्रमशः माध्य से रीडिंग।
Note - यदि मानक विचलन का मूल्य छोटा है, तो माप के पढ़ने के मूल्यों में अधिक सटीकता होगी।
झगड़ा
मानक विचलन का वर्ग कहा जाता है variance। गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$$V=\sigma^{2}$$
कहाँ पे,
$V$ विचरण है
$\sigma$ मानक विचलन है
विचलन का माध्य वर्ग भी कहा जाता है variance। गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$$V=\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N}$$
उपरोक्त सूत्र मान्य है यदि रीडिंग की संख्या, N 20 से अधिक या उसके बराबर है। हम विचरण के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं जब रीडिंग की संख्या, N 20 से कम हो।
$$V=\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N-1}$$
कहाँ पे,
$V$ विचरण है
$d_{1}, d_{2}, d_{3}, …, d_{N}$ पहले, दूसरे, तीसरे,… के विचलन हैं $N^{th}$ क्रमशः माध्य से रीडिंग।
इसलिए, सांख्यिकीय मापदंडों की मदद से, हम किसी विशेष माप की रीडिंग का विश्लेषण कर सकते हैं। इस तरह, हम अधिक सटीक माप मान प्राप्त करेंगे।
किसी भी मात्रा को मापने के लिए उपयोग किए जाने वाले उपकरणों को कहा जाता है measuring instruments। यदि उपकरण बुनियादी विद्युत मात्राओं को माप सकते हैं, जैसे कि वोल्टेज और वर्तमान के रूप में जाना जाता हैbasic measuring instruments।
बुनियादी माप उपकरणों के प्रकार
हम बुनियादी माप उपकरणों को निम्नलिखित दो प्रकारों में वर्गीकृत कर सकते हैं।
- Voltmeters
- Ammeters
आइए हम इन दो बुनियादी माप उपकरणों के बारे में संक्षेप में चर्चा करें।
voltmeters
जैसा कि नाम सुझाव देता है, voltmeterएक मापक यंत्र है जो किसी विद्युत परिपथ के दो बिंदुओं पर वोल्टेज को मापता है। वोल्टेज की इकाइयाँ वोल्ट हैं और मापने का यंत्र मीटर है। इसलिए, शब्द "वोल्टमीटर" दो शब्दों के संयोजन से प्राप्त होता है“volt” तथा “meter”।
हम वोल्टमीटर को निम्नलिखित में वर्गीकृत कर सकते हैं two types वोल्टेज के प्रकार के आधार पर जिसे वह माप सकता है।
- डीसी वाल्टमीटर
- एसी वोल्टमीटर
डीसी वाल्टमीटर
जैसा कि नाम से पता चलता है, डीसी वाल्टमीटर मापता है DC voltageएक इलेक्ट्रिक सर्किट के किसी भी दो बिंदुओं के पार। एक व्यावहारिक डीसी वाल्टमीटर नीचे दिए गए आंकड़े में दिखाया गया है।

चित्र में दिखाया गया डीसी वाल्टमीटर एक है $(0-10)V$ DC voltmeter। इसलिए, इसका उपयोग शून्य वोल्ट से 10 वोल्ट तक डीसी वोल्टेज को मापने के लिए किया जा सकता है
एसी वाल्टमीटर
जैसा कि नाम से पता चलता है, AC वाल्टमीटर मापता है AC voltageएक इलेक्ट्रिक सर्किट के किसी भी दो बिंदुओं के पार। एक व्यावहारिक एसी वाल्टमीटर नीचे दिए गए आंकड़े में दिखाया गया है।

उपरोक्त आकृति में दिखाया गया एसी वाल्टमीटर एक है $(0-250)V$ AC voltmeter। इसलिए, इसका उपयोग शून्य वोल्ट से 250 वोल्ट तक एसी वोल्टेज को मापने के लिए किया जा सकता है
Ammeters
जैसा कि नाम सुझाव देता है, ammeterएक मापने वाला उपकरण है जो विद्युत सर्किट के किसी भी दो बिंदुओं के माध्यम से बहने वाले वर्तमान को मापता है। करंट की इकाई एम्पीयर है और मापने का यंत्र मीटर है। शब्द "एमीटर" संयोजन द्वारा प्राप्त किया गया है“am” के साथ एम्पीयर “meter”।
हम एमीटर्स को निम्नलिखित में वर्गीकृत कर सकते हैं two types वर्तमान के प्रकार के आधार पर जिसे वह माप सकता है।
- डीसी Ammeters
- एसी एममीटर
डीसी Ammeter
जैसा कि नाम से पता चलता है, डीसी एमीटर मापक है DC currentयह विद्युत परिपथ के किसी भी दो बिंदुओं से होकर बहता है। एक व्यावहारिक डीसी एमीटर को चित्र में दिखाया गया है।

उपरोक्त आकृति में दिखाया गया डीसी एमीटर है a $(0-50)A$ DC ammeter। इसलिए, इसका उपयोग शून्य धाराओं से 50 एम्पीयर तक डीसी धाराओं को मापने के लिए किया जा सकता है
एसी एमीटर
जैसा कि नाम से पता चलता है, एसी एमीटर मापक है AC currentयह विद्युत परिपथ के किसी भी दो बिंदुओं से होकर बहता है। एक व्यावहारिक एसी एमीटर नीचे दिए गए आंकड़े में दिखाया गया है।

उपरोक्त आकृति में दिखाया गया एसी एमीटर एक है $(0-100)A$ AC ammeter। इसलिए, इसका उपयोग शून्य धाराओं से 100 एम्पीयर तक एसी धाराओं को मापने के लिए किया जा सकता है।
हम निम्नलिखित कुछ अध्यायों में विभिन्न वोल्टमीटर और एमीटर के बारे में विस्तार से चर्चा करेंगे
डीसी वाल्टमीटर एक मापक यंत्र है, जिसका उपयोग डीसी सर्किट को विद्युत सर्किट के किसी भी दो बिंदुओं पर मापने के लिए किया जाता है। यदि हम स्थायी चुंबक मूविंग कॉइल (पीएमएमसी) गैल्वेनोमीटर के साथ श्रृंखला में एक अवरोधक रखते हैं, तो पूरे क्षेत्र एक साथ मिलकरDC voltmeter।
श्रृंखला प्रतिरोध, जिसका उपयोग डीसी वाल्टमीटर में किया जाता है, को श्रृंखला गुणक प्रतिरोध या बस गुणक भी कहा जाता है। यह मूल रूप से वर्तमान की मात्रा को सीमित करता है जो गैल्वेनोमीटर के माध्यम से बहती है ताकि मीटर के वर्तमान को पूर्ण पैमाने पर विक्षेपण मूल्य से अधिक रोका जा सके। circuit diagram डीसी वाल्टमीटर का आंकड़ा नीचे दिखाया गया है।
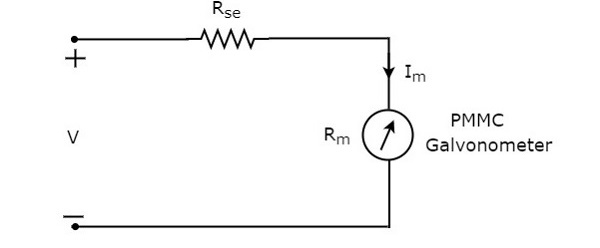
हमें इस डीसी वोल्टमीटर को एक इलेक्ट्रिक सर्किट के दो बिंदुओं पर रखना होगा, जहां डीसी वोल्टेज को मापा जाना है।
लागू KVL ऊपर सर्किट के पाश के आसपास।
$V-I_{m}R_{se}-I_{m}R_{m}=0$ (समीकरण 1)
$$\Rightarrow V-I_{m}R_{m}=I_{m}R_{se}$$
$$\Rightarrow R_{se}=\frac{V-I_{m}R_{m}}{I_{m}}$$
$\Rightarrow R_{se}=\frac{V}{I_{m}}-R_{m}$ (समीकरण 2)
कहाँ पे,
$R_{se}$ श्रृंखला गुणक प्रतिरोध है
$V$ पूरी श्रृंखला डीसी वोल्टेज है जिसे मापा जाना है
$I_{m}$ पूर्ण पैमाने पर विक्षेपण धारा है
$R_{m}$ गैल्वेनोमीटर का आंतरिक प्रतिरोध है
पूर्ण श्रेणी डीसी वोल्टेज का अनुपात जिसे मापा जाना है, $V$ और डीसी वोल्टेज ड्रॉप गैल्वेनोमीटर में, $V_{m}$ जाना जाता है multiplying factor, म। गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$m=\frac{V}{V_{m}}$ (समीकरण 3)
समीकरण 1 से, हम निम्नलिखित समीकरण प्राप्त करेंगे full range DC voltage जिसे मापा जाना है, $V$।
$V=I_{m}R_{se}+I_{m}R_{m}$ (समीकरण 4)
DC voltage drop गैल्वेनोमीटर के पार, $V_{m}$ पूर्ण पैमाने पर विक्षेपण धारा का उत्पाद है, $I_{m}$ और गैल्वेनोमीटर का आंतरिक प्रतिरोध, $R_{m}$। गणितीय रूप से, इसे लिखा जा सकता है
$V_{m}=I_{m}R_{m}$ (समीकरण 5)
Substitute, समीकरण 4 और समीकरण 5 में समीकरण 3।
$$m=\frac{I_{m}R_{se}+I_{m}R_{m}}{I_{m}R_{m}}$$
$\Rightarrow m=\frac{R_{se}}{R_{m}}+1$
$\Rightarrow m-1=\frac{R_{se}}{R_{m}}$
$R_{se}=R_{m}\left (m-1 \right )$(समीकरण 6)
हम पा सकते हैं value of series multiplier resistance उपलब्ध आंकड़ों के आधार पर समीकरण 2 या समीकरण 6 का उपयोग करके।
मल्टी रेंज डीसी वोल्टमीटर
पिछले अनुभाग में, हमने डीसी वाल्टमीटर पर चर्चा की थी, जिसे पीएमएमसी गैलोमोमीटर के साथ श्रृंखला में गुणक रोकनेवाला द्वारा प्राप्त किया जाता है। इस डीसी वाल्टमीटर का उपयोग मापने के लिए किया जा सकता हैparticular range डीसी वोल्टेज की।
यदि हम DC वोल्टमीटर का उपयोग डीसी वोल्टेज को मापने के लिए करना चाहते हैं multiple ranges, तो हमें एकल गुणक रोकनेवाला के बजाय कई समानांतर गुणक प्रतिरोधों का उपयोग करना होगा और प्रतिरोधों का यह पूरा संयोजन पीएमएमसी गैल्वेनोमीटर के साथ श्रृंखला में है। circuit diagram मल्टी रेंज डीसी वाल्टमीटर नीचे दिए गए आंकड़े में दिखाया गया है।
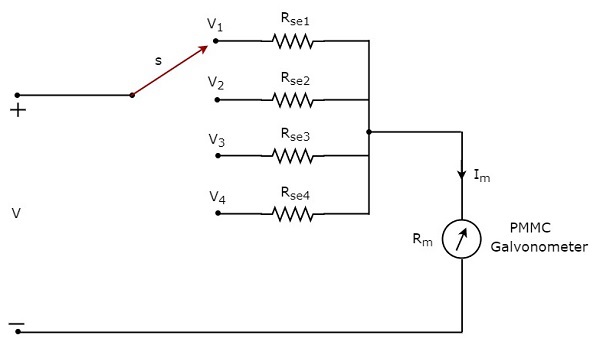
हमें इसे जगह देनी होगी multi range DC voltmeterएक इलेक्ट्रिक सर्किट के दो बिंदुओं पर, जहां आवश्यक रेंज के डीसी वोल्टेज को मापा जाना है। हम स्विच एस को संबंधित गुणक रोकने वाले से कनेक्ट करके वोल्टेज की वांछित सीमा चुन सकते हैं।
चलो, $m_{1},m_{2}, m_{2} $ तथा $m_{4}$ हैं multiplying factors डीसी वाल्टमीटर का जब हम पूर्ण श्रेणी के डीसी वोल्टेज को मापते हैं, $V_{1} , V_{2}, V_{3}$ तथा $V_{4}$क्रमशः। प्रत्येक गुणन कारक के अनुरूप सूत्र निम्नलिखित हैं।
$$m_{1}=\frac{V_{1}}{V_{m}}$$
$$m_{2}=\frac{V_{2}}{V_{m}}$$
$$m_{3}=\frac{V_{3}}{V_{m}}$$
$$m_{4}=\frac{V_{4}}{V_{m}}$$
उपरोक्त सर्किट में, चार हैं series multiplier resistors, $R_{se1}, R_{se2}, R_{se3}$ तथा $R_{se4}$। इन चार प्रतिरोधों के अनुरूप सूत्र निम्नलिखित हैं।
$$R_{se1}=R_{m}\left (m_{1}-1 \right )$$
$$R_{se2}=R_{m}\left (m_{2}-1 \right )$$
$$R_{se3}=R_{m}\left (m_{3}-1 \right )$$
$$R_{se4}=R_{m}\left (m_{4}-1 \right )$$
इसलिए, हम उपरोक्त सूत्रों का उपयोग करके प्रत्येक श्रृंखला गुणक रोकनेवाला के प्रतिरोध मान पा सकते हैं।
वह उपकरण, जिसका उपयोग विद्युत परिपथ के किसी भी दो बिंदुओं पर AC वोल्टेज को मापने के लिए किया जाता है, कहा जाता है AC voltmeter। यदि एसी वाल्टमीटर में रेक्टिफायर होता है, तो इसे रेक्टिफायर आधारित एसी वाल्टमीटर कहा जाता है।
डीसी वाल्टमीटर केवल डीसी वोल्टेज को मापता है। यदि हम इसका उपयोग एसी वोल्टेज को मापने के लिए करना चाहते हैं, तो हमें इन दो चरणों का पालन करना होगा।
Step1 - एसी वोल्टेज सिग्नल को रेक्टिफायर का उपयोग करके डीसी वोल्टेज सिग्नल में बदलें।
Step2 - रेक्टिफायर के आउटपुट सिग्नल के डीसी या औसत मूल्य को मापें।
हमें मिला Rectifier based AC voltmeter, मूल डीसी वाल्टमीटर को सही करनेवाला सर्किट शामिल करके। यह अध्याय रेक्टिफायर आधारित एसी वोल्टमीटर के बारे में बताता है।
रेक्टिफायर आधारित एसी वोल्टमीटर के प्रकार
निम्नलिखित हैं two types रेक्टिफायर आधारित एसी वोल्टमीटर।
- हाफ वेव रेक्टिफायर का उपयोग करके एसी वाल्टमीटर
- फुल वेव रेक्टिफायर का उपयोग करके एसी वाल्टमीटर
अब, हम एक-एक करके इन दो एसी वोल्टमीटर के बारे में चर्चा करते हैं।
हाफ वेव रेक्टिफायर का उपयोग कर एसी वोल्टमीटर
यदि एक आधा लहर सही करनेवाला डीसी वाल्टमीटर से आगे जुड़ा हुआ है, तो उस पूरे संयोजन को आधा लहर प्रवर्धक का उपयोग करके एसी वोल्टमीटर कहा जाता है। block diagram हाफ वेव रेक्टिफायर का उपयोग करने वाले एसी वोल्टमीटर को नीचे दिए गए आंकड़े में दिखाया गया है।
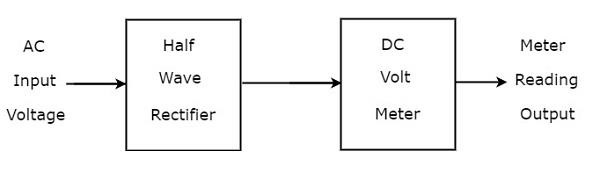
उपरोक्त ब्लॉक आरेख में दो ब्लॉक होते हैं: आधा लहर आयताकार और डीसी वाल्टमीटर। हम उपरोक्त ब्लॉक आरेख में संबंधित घटक (ओं) के साथ प्रत्येक ब्लॉक को बदलकर संबंधित सर्किट आरेख प्राप्त करेंगे। ऐसाcircuit diagram हाफ वेव रेक्टिफायर का उपयोग करने वाले एसी वाल्टमीटर जैसा दिखेगा जैसा कि नीचे दिए गए आंकड़े में दिखाया गया है।
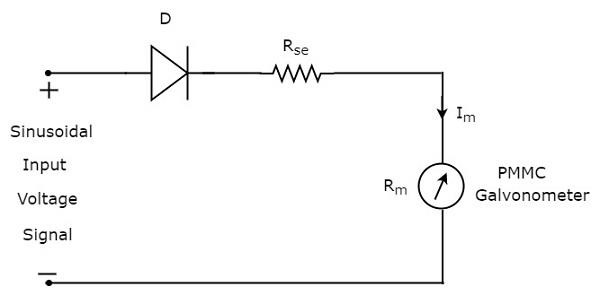
rms value साइनसोइडल (AC) इनपुट वोल्टेज सिग्नल है
$$V_{rms}=\frac{V_{m}}{\sqrt{2}}$$
$$\Rightarrow V_{m}=\sqrt{2} V_{rms}$$
$$\Rightarrow V_{m}=1.414 V_{rms}$$
कहाँ पे,
$V_{m}$ साइनसोइडल (एसी) इनपुट वोल्टेज सिग्नल का अधिकतम मूल्य है।
DC या हाफ वेव रेक्टिफायर के आउटपुट सिग्नल का औसत मूल्य है
$$V_{dc}=\frac{V_{m}}{\pi}$$
Substitute, का मूल्य $V_{m}$ उपरोक्त समीकरण में।
$$V_{dc}= \frac{1.414 V_{rms}}{\pi}$$
$$V_{dc}= 0.45 V_{rms}$$
इसलिए, एसी वोल्टमीटर एक आउटपुट वोल्टेज का उत्पादन करता है, जो इसके बराबर है 0.45 साइनसोइडल (एसी) इनपुट वोल्टेज सिग्नल के आरएमएस मूल्य
फुल वेव रेक्टिफायर का उपयोग करके एसी वाल्टमीटर
यदि एक पूर्ण लहर सही करनेवाला डीसी वाल्टमीटर से आगे जुड़ा हुआ है, तो उस पूरे संयोजन को पूर्ण तरंग प्रवर्धक का उपयोग करके एसी वाल्टमीटर कहा जाता है। block diagram फुल वेव रेक्टिफायर का उपयोग करने वाले एसी वोल्टमीटर को नीचे दिए गए आंकड़े में दिखाया गया है
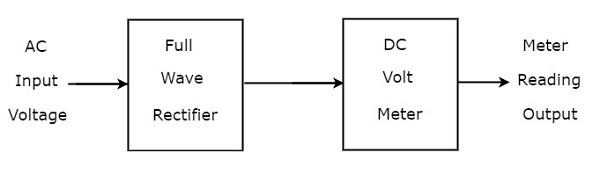
उपरोक्त ब्लॉक आरेख में दो ब्लॉक होते हैं: पूर्ण तरंग सुधारक और डीसी वाल्टमीटर। हम उपरोक्त ब्लॉक आरेख में संबंधित घटक (ओं) के साथ प्रत्येक ब्लॉक को बदलकर संबंधित सर्किट आरेख प्राप्त करेंगे।
ऐसा circuit diagram फुल वेव रेक्टिफायर का उपयोग करने वाले एसी वाल्टमीटर नीचे की आकृति में दिखाए गए अनुसार दिखेंगे।
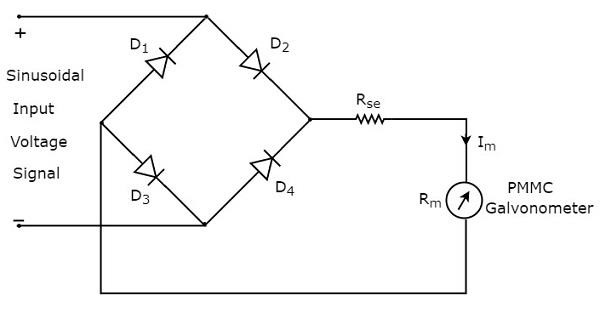
rms value साइनसोइडल (AC) इनपुट वोल्टेज सिग्नल है
$$V_{rms}=\frac{V_{m}}{\sqrt{2}}$$
$$\Rightarrow V_{m}=\sqrt{2} \:V_{rms}$$
$$\Rightarrow V_{m}= 1.414 V_{rms}$$
कहाँ पे,
$V_{m}$ साइनसोइडल (एसी) इनपुट वोल्टेज सिग्नल का अधिकतम मूल्य है।
DC या फुल वेव रेक्टिफायर के आउटपुट सिग्नल का औसत मूल्य है
$$V_{dc}=\frac{2V_{m}}{\pi}$$
Substitute, का मूल्य $V_{m}$ उपरोक्त समीकरण में
$$V_{dc}=\frac{2\times 1.414 \:V_{rms}}{\pi}$$
$$V_{dc}=0.9 \:V_{rms}$$
इसलिए, एसी वोल्टमीटर एक आउटपुट वोल्टेज का उत्पादन करता है, जो इसके बराबर है 0.9 साइनसोइडल (एसी) इनपुट वोल्टेज सिग्नल के आरएमएस मूल्य।
पिछले अध्याय में, हमने रेक्टिफायर आधारित एसी वोल्टमीटर के बारे में चर्चा की। यह अध्याय निम्नलिखित दो प्रकार के एसी वोल्टमीटर को कवर करता है।
- पीक रिस्पांस AC वोल्टमीटर
- एसी वोल्टमीटर का जवाब देने वाला सच्चा आरएमएस
अब, हम एक-एक करके इन दो प्रकार के एसी वोल्टमीटर के बारे में चर्चा करते हैं।
पीक रिस्पांसिंग एसी वोल्टमीटर
जैसा कि नाम से ही पता चलता है कि चोटी का जवाब देने वाला एसी वोल्टमीटर जवाब देता है peak valuesएसी वोल्टेज सिग्नल की। इसका मतलब है कि, यह वाल्टमीटर एसी वोल्टेज के शिखर मूल्यों को मापता है। circuit diagram पीक रिस्पांसिंग एसी वाल्टमीटर नीचे दिखाया गया है -
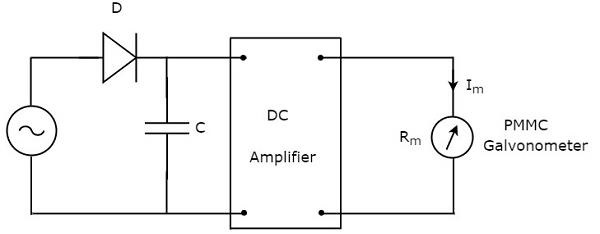
उपरोक्त सर्किट में एक डायोड, कैपेसिटर, डीसी एम्पलीफायर और पीएमएमसी गैल्वेनोमीटर शामिल हैं। उपरोक्त सर्किट में मौजूद डायोड का उपयोग सुधार के उद्देश्य से किया जाता है। तो, डायोड एसी वोल्टेज सिग्नल को एक डीसी वोल्टेज सिग्नल में परिवर्तित करता है। संधारित्र इस डीसी वोल्टेज सिग्नल के चरम मूल्य पर चार्ज करता है।
दौरान positive half cycleएसी वोल्टेज सिग्नल, डायोड कंडक्ट करता है और कैपेसिटर एसी वोल्टेज सिग्नल के पीक वैल्यू पर चार्ज होता है। जब एसी वोल्टेज सिग्नल का मान इस मान से कम होता है, तो डायोड रिवर्स बायस्ड हो जाएगा।
इस प्रकार, एसी वोल्टेज सिग्नल के अगले सकारात्मक आधे चक्र तक डीसी एम्पलीफायर के अवरोधक के माध्यम से संधारित्र का निर्वहन होगा। जब एसी वोल्टेज सिग्नल का मान कैपेसिटर वोल्टेज से अधिक होता है, तो डायोड का संचालन होता है और इस प्रक्रिया को दोहराया जाएगा।
हमें घटक मूल्यों को इस तरह से चुनना चाहिए कि संधारित्र तेजी से चार्ज करता है और धीरे-धीरे निर्वहन करता है। नतीजतन, मीटर हमेशा इस कैपेसिटर वोल्टेज का जवाब देता है, अर्थातpeak value of AC voltage।
एसी वोल्टमीटर का जवाब देने वाला सच्चा आरएमएस
जैसा कि नाम से ही पता चलता है, AC वोल्टमीटर का जवाब देने वाला सही RMS AC वोल्टेज सिग्नल के सही RMS मानों पर प्रतिक्रिया करता है। यह वाल्टमीटर एसी वोल्टेज के आरएमएस मूल्यों को मापता है। circuit diagram सही आरएमएस का जवाब देने वाला एसी वोल्टमीटर नीचे दिए गए आंकड़े में दिखाया गया है।
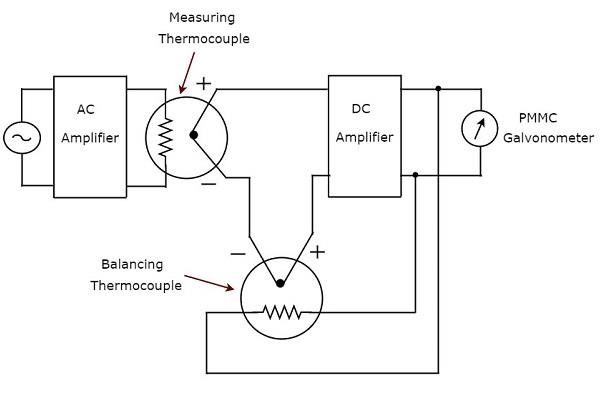
उपर्युक्त सर्किट में एक एसी एम्पलीफायर, दो थर्मोकॉल, डीसी एम्पलीफायर और पीएमएमसी गैल्वेनोमीटर शामिल हैं। एसी एम्पलीफायर एसी वोल्टेज सिग्नल को बढ़ाता है। उपरोक्त सर्किट में उपयोग किए जाने वाले दो थर्मोकॉल्स एक मापने वाले थर्मोकपल और एक संतुलन वाले थर्मोकपल हैं।Measuring thermocouple एक आउटपुट वोल्टेज पैदा करता है, जो AC वोल्टेज सिग्नल के RMS मान के समानुपाती होता है।
कोई भी थर्मोकपल इनपुट मात्रा के एक वर्ग को सामान्य मात्रा में परिवर्तित करता है। इसका मतलब है कि थर्मोकपल के आउटपुट और इनपुट के बीच एक गैर-रैखिक संबंध मौजूद है। प्रतिक्रिया सर्किट में एक और थर्मोकपल का उपयोग करके गैर-रैखिक व्यवहार के गैर-रैखिक व्यवहार के प्रभाव को उपेक्षित किया जा सकता है। उपरोक्त सर्किट में इस उद्देश्य के लिए उपयोग किया जाने वाला थर्मोकपल के रूप में जाना जाता हैbalancing thermocouple।
दो thermocouples, अर्थात् thermocouple को मापने और एक साथ डीसी एम्पलीफायर के इनपुट पर एक दुल्हन के रूप में संतुलन thermocouple। नतीजतन, मीटर हमेशा प्रतिक्रिया करता हैtrue RMS value एसी वोल्टेज सिग्नल की।
वर्तमान विद्युत आवेश के प्रवाह की दर है। यदि यह विद्युत आवेश केवल एक दिशा में बहता है, तो परिणामी धारा को Direct Current (DC) कहा जाता है। वह साधन, जिसका उपयोग डायरेक्ट करंट को मापने के लिए किया जाता हैDC ammeter।
यदि हम स्थायी चुंबक मूविंग कॉइल (PMMC) गैल्वेनोमीटर के समानांतर एक अवरोधक रखते हैं, तो संपूर्ण संयोजन DC एमीटर के रूप में कार्य करता है। समानांतर प्रतिरोध, जिसका उपयोग डीसी एमीटर में किया जाता है, को शंट प्रतिरोध या बस, कहा जाता हैshunt। बड़े मूल्य के डीसी वर्तमान को मापने के लिए इस प्रतिरोध के मूल्य को छोटा माना जाना चाहिए।
circuit diagram डीसी एमीटर का चित्र नीचे दिया गया है।
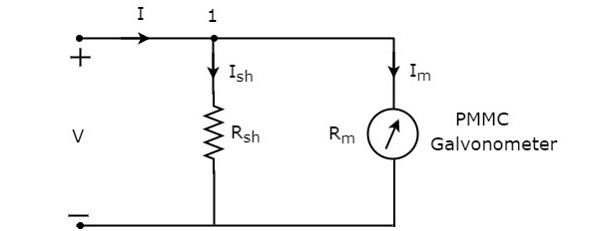
हमें इसे जगह देनी होगी DC ammeterएक विद्युत सर्किट की शाखा के साथ श्रृंखला में, जहां डीसी वर्तमान को मापा जाना है। तत्वों में वोल्टेज, जो समानांतर में जुड़े हुए हैं, समान है। तो, अलग धकेलना रोकनेवाला में वोल्टेज,$R_{sh}$ और गैल्वेनोमीटर प्रतिरोध भर में वोल्टेज, $R_{m}$ वही है, क्योंकि उन दो तत्वों को उपरोक्त सर्किट में समानांतर में जोड़ा जाता है। Mathematically, यह लिखा जा सकता है
$$I_{sh}R_{sh}=I_{m}R_{m}$$
$\Rightarrow R_{sh}=\frac{I_{m}R_{m}}{I_{sh}}$ (समीकरण 1)
KCL equation नोड 1 पर है
$$-I+I_{sh}+I_{m}=0$$
$$\Rightarrow I_{sh}=I-I_{m}$$
Substitute का मूल्य $I_{sh}$ समीकरण 1 में।
$R_{sh}=\frac{I_{m}R_{m}}{I-I_{m}}$(समीकरण 2)
लेना, $I_{m}$ हर शब्द में सामान्य है, जो समीकरण 2 के दाहिने हाथ में मौजूद है
$$R_{sh}=\frac{I_{m}R_{m}}{I_{m}(\frac{1}{I_{m}}-1)}$$
$\Rightarrow R_{sh}=\frac{R_{m}}{\frac{I}{I_{m}}-1}$(समीकरण 3)
कहाँ पे,
$R_{sh}$ शंट प्रतिरोध है
$R_{m}$ गैल्वेनोमीटर का आंतरिक प्रतिरोध है
$I$ कुल प्रत्यक्ष करंट है जिसे मापा जाना है
$I_{m}$ पूर्ण पैमाने पर विक्षेपण धारा है
कुल प्रत्यक्ष धारा का अनुपात जिसे मापा जाना है, $I$ और गैल्वेनोमीटर का पूर्ण पैमाने पर विक्षेपण धारा, $I_{m}$ जाना जाता है multiplying factor, m। गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$m=\frac{I}{I_{m}}$(समीकरण 4)
$R_{sh}=\frac{R_{m}}{m-1}$(समीकरण 5)
हम पा सकते हैं value of shunt resistance उपलब्ध डेटा के आधार पर समीकरण 2 या समीकरण 5 का उपयोग करके।
मल्टी रेंज डीसी एमीटर
पिछले अनुभाग में, हमने डीसी एमीटर के बारे में चर्चा की जो कि पीएमएमसी गैल्वेनोमीटर के समानांतर एक रोकनेवाला रखकर प्राप्त की जाती है। इस डीसी एमीटर का उपयोग मापने के लिए किया जा सकता हैparticular range प्रत्यक्ष मुद्राओं की।
अगर हम DC केमीटर को डायरेक्ट करंट के माप के लिए इस्तेमाल करना चाहते हैं multiple ranges, तब हमें एकल प्रतिरोधक के बजाय कई समानांतर प्रतिरोधों का उपयोग करना होगा और प्रतिरोधों का यह पूरा संयोजन पीएमएमसी गैल्वेनोमीटर के समानांतर है। circuit diagram मल्टी रेंज डीसी एमीटर नीचे चित्र में दिखाया गया है।
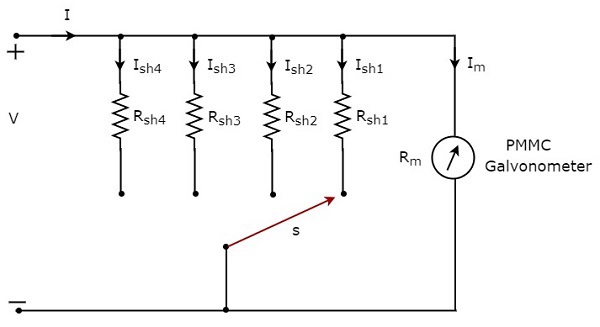
इस मल्टी रेंज डीसी एमीटर को एक इलेक्ट्रिक सर्किट की शाखा के साथ श्रृंखला में रखें, जहां आवश्यक सीमा के डायरेक्ट करंट को मापा जाना है। धाराओं की वांछित सीमा स्विच को संबंधित शंट अवरोधक से जोड़कर चुना जाता है।
चलो, $m_{1}, m_{2}, m_{3}$ तथा $m_{4}$ हैं multiplying factors डीसी एमीटर जब हम मानते हैं कि कुल प्रत्यक्ष धाराओं को मापा जाएगा, $I_{1}, I_{2}, I_{3}$ तथा $I_{4}$क्रमशः। प्रत्येक गुणन कारक के अनुरूप सूत्र निम्नलिखित हैं।
$$m_{1}=\frac{I_{1}}{I_{m}}$$
$$m_{2}=\frac{I_{2}}{I_{m}}$$
$$m_{3}=\frac{I_{3}}{I_{m}}$$
$$m_{4}=\frac{I_{4}}{I_{m}}$$
उपरोक्त सर्किट में, चार हैं shunt resistors, $R_{sh1}, R_{sh2}, R_{sh2}$ तथा $R_{sh4}$। इन चार प्रतिरोधों के अनुरूप सूत्र निम्नलिखित हैं।
$$R_{sh1}=\frac{R_{m}}{m_{1}-1}$$
$$R_{sh2}=\frac{R_{m}}{m_{2}-1}$$
$$R_{sh3}=\frac{R_{m}}{m_{3}-1}$$
$$R_{sh4}=\frac{R_{m}}{m_{4}-1}$$
उपरोक्त सूत्र हमें प्रत्येक शंट रोकनेवाला के प्रतिरोध मूल्यों को खोजने में मदद करेंगे।
वर्तमान विद्युत आवेश के प्रवाह की दर है। यदि इस विद्युत आवेश की दिशा नियमित रूप से बदलती है, तो परिणामी धारा को कहा जाता हैAlternating Current (AC)।
वह उपकरण, जिसका उपयोग इलेक्ट्रिक सर्किट की किसी भी शाखा से प्रवाहित होने वाली प्रत्यावर्ती धारा को मापने के लिए किया जाता है AC ammeter।
Example - थर्मोकपल प्रकार एसी एमीटर।
अब, थर्मोकपल प्रकार के एसी एमीटर के बारे में चर्चा करते हैं।
थर्मोकपल प्रकार एसी एमीटर
यदि पीएमएमसी गैल्वेनोमीटर के आगे एक थर्मोकपल जुड़ा हुआ है, तो उस पूरे संयोजन को थर्मोकपल प्रकार एसी एमीटर कहा जाता है। block diagram थर्मोकपल प्रकार का एसी एमीटर नीचे दिए गए आंकड़े में दिखाया गया है।
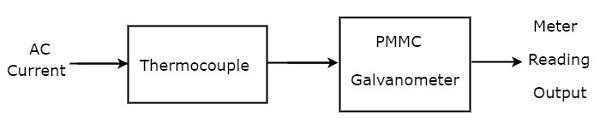
उपरोक्त ब्लॉक आरेख में मुख्य रूप से दो ब्लॉक होते हैं: एक थर्मोकपल और एक पीएमएमसी गैल्वेनोमीटर। हम उपरोक्त ब्लॉक आरेख में संबंधित घटक (ओं) के साथ प्रत्येक ब्लॉक को बदलकर संबंधित सर्किट आरेख प्राप्त करेंगे। ऐसाcircuit diagram थर्मोकपल प्रकार के एसी एमीटर नीचे की तरह दिखाई देंगे।
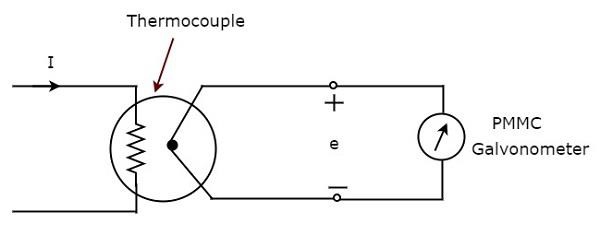
थर्मोकपल एक ईएमएफ उत्पन्न करता है, $e$, जब भी प्रत्यावर्ती धारा, मैं हीटर तत्व से बहती है। यह EMF,$e$वर्तमान के आरएमएस मूल्य के सीधे आनुपातिक है, मैं हीटर तत्व के माध्यम से बह रहा हूं। इसलिए, हमें पढ़ने के लिए PMMC साधन के पैमाने को जांचना होगाrms values of current।
इसलिए, इस अध्याय के साथ हमने सभी बुनियादी मापक यंत्र जैसे कि डीसी वोल्टमीटर, एसी वोल्टमीटर, डीसी एमीटर और एसी एमीटर को पूरा किया है। अगले अध्याय में, हम मीटर या मापने वाले उपकरणों के बारे में चर्चा करते हैं, जो प्रतिरोध मूल्य को मापते हैं।
वह उपकरण, जिसका उपयोग इलेक्ट्रिक सर्किट में किन्हीं दो बिंदुओं के बीच प्रतिरोध के मान को मापने के लिए किया जाता है ohmmeter। इसका उपयोग अज्ञात अवरोधक के मूल्य को खोजने के लिए भी किया जा सकता है। प्रतिरोध की इकाइयाँ ओम हैं और मापक यंत्र मीटर है। तो, "ओममीटर" शब्द शब्दों के संयोजन से प्राप्त होता है“ohm” तथा “meter”।
ओहमीटर्स के प्रकार
निम्नलिखित हैं two types ओम्मेटेटर्स का।
- सीरीज ओह्मोटर
- शंट ओह्मोटर
अब, हम एक-एक करके ओममीटर के इन दो प्रकारों के बारे में चर्चा करते हैं।
सीरीज ओह्मोटर
यदि अवरोधक का मान अज्ञात है और उसे ओममीटर के साथ श्रृंखला में रखकर मापा जाना है, तो उस ओममीटर को श्रृंखला ओममीटर कहा जाता है। circuit diagram श्रृंखला के ओममिटर को नीचे दिए गए आंकड़े में दिखाया गया है।
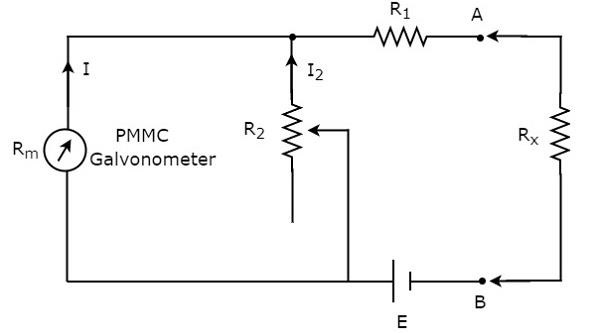
सर्किट का हिस्सा, जो टर्मिनलों के बाईं ओर A & B है series ohmmeter। इसलिए, हम अज्ञात प्रतिरोध के मूल्य को टर्मिनलों ए और बी के दाईं ओर रखकर माप सकते हैं। अब बी के बारे में चर्चा करते हैं।calibration scale ओहियोमीटर की श्रृंखला।
अगर $R_{x}= 0 \:\Omega$, फिर टर्मिनलों A & B को एक दूसरे के साथ परिचालित किया जाएगा। तो, मीटर करंट प्रतिरोधों के बीच विभाजित हो जाता है,$R_{1}$ तथा $R_{2}$। अब, रोकनेवाला का मान भिन्न होता है,$R_{2}$ इस तरह से कि पूरा मीटर करंट रेसिस्टर से होकर बहता है, $R_{1}$केवल। इस मामले में, मीटर पूर्ण दिखाता हैscale deflection current। इसलिए, मीटर के इस पूर्ण पैमाने पर विक्षेपण धारा को इस रूप में दर्शाया जा सकता है$0 \:\Omega$।
अगर $R_{x}= \infty \:\Omega$, तब टर्मिनलों ए और बी एक दूसरे के साथ खुले सर्कुलेट किए जाएंगे। इसलिए, कोई भी प्रवाह अवरोधक के माध्यम से नहीं बहता है,$R_{1}$। इस मामले में, मीटर अशक्त विक्षेपन को दर्शाता है। इसलिए, मीटर के इस अशक्त विक्षेपण का प्रतिनिधित्व किया जा सकता है$\infty \Omega$।
इस तरह, के विभिन्न मूल्यों पर विचार करके $R_{x}$, मीटर विभिन्न विक्षेप दिखाता है। इसलिए, तदनुसार हम उन प्रतिरोधों को संबंधित प्रतिरोध मान के साथ दर्शा सकते हैं।
श्रृंखला ओम्मीटर में एक अंशांकन पैमाने होता है। इसमें 0 के संकेत हैं$\Omega$ तथा $\infty \:\Omega$क्रमशः दाहिने हाथ और बाएं हाथ के अंतिम बिंदुओं पर। श्रृंखला ओमममीटर मापने के लिए उपयोगी हैhigh values of resistances.
शंट ओह्मोटर
यदि रोकनेवाला का मूल्य अज्ञात है और इसे ओममीटर के साथ समानांतर (शंट) में रखकर मापा जाना है, तो उस ओममीटर को शंट ओममीटर कहा जाता है। circuit diagram शंट ओह्मोटर को नीचे दिए गए आंकड़े में दिखाया गया है।
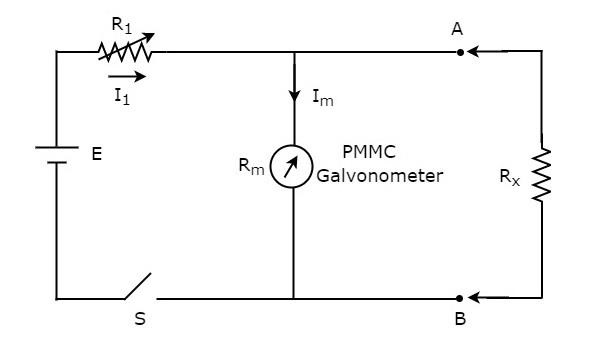
सर्किट का हिस्सा, जो टर्मिनलों के बाईं ओर A & B है shunt ohmmeter। इसलिए, हम अज्ञात प्रतिरोध के मूल्य को टर्मिनलों A & B के दाईं ओर रखकर माप सकते हैं।
अब, हम के बारे में चर्चा करते हैं calibration scaleशंट ओह्मोटर का। उपर्युक्त सर्किट के स्विच को बंद करें, जबकि यह उपयोग में है।
अगर $R_{x}=0 \:\Omega$, फिर टर्मिनलों A & B को एक दूसरे के साथ परिचालित किया जाएगा। इसके कारण, संपूर्ण वर्तमान,$I_{1}$टर्मिनलों ए और बी के माध्यम से बहती है इस मामले में, पीएमएमसी गैल्वेनोमीटर के माध्यम से कोई वर्तमान प्रवाह नहीं होता है। इसलिएnull deflection PMMC गैल्वेनोमीटर के रूप में प्रतिनिधित्व किया जा सकता है $0 \:\Omega$।
अगर $R_{x}=\infty \:\Omega$, तब टर्मिनलों ए और बी एक दूसरे के साथ खुले सर्कुलेट किए जाएंगे। इसलिए, कोई भी प्रवाह टर्मिनलों ए और बी से नहीं बहता है। इस मामले में, पूरा वर्तमान,$I_{1}$पीएमएमसी गैल्वेनोमीटर से होकर बहती है। यदि आवश्यक हो, तो रोकनेवाला का मान अलग-अलग (समायोजित) करें,$R_{1}$जब तक PMMC गैल्वेनोमीटर पूर्ण पैमाने पर विक्षेपन करंट दिखाता है। इसलिए, यहfull scale deflection PMMC गैल्वेनोमीटर के वर्तमान के रूप में प्रतिनिधित्व किया जा सकता है $\infty \:\Omega$
इस तरह, के विभिन्न मूल्यों पर विचार करके $R_{x}$, मीटर विभिन्न विक्षेप दिखाता है। इसलिए, तदनुसार हम उन प्रतिरोधों को संबंधित प्रतिरोध मूल्यों के साथ दर्शा सकते हैं।
शंट ओममीटर में एक अंशांकन पैमाने होते हैं। इसके संकेत मिलते हैं$0 \:\Omega$ तथा $\infty \:\Omega$ क्रमशः बाएं हाथ के अंतिम बिंदु और दाएं हाथ के पैमाने पर।
शंट ओममीटर मापने के लिए उपयोगी है low values of resistances। इसलिए, हम या तो श्रृंखला ओममीटर का उपयोग कर सकते हैं या प्रतिरोधों के मूल्यों के आधार पर ओममीटर को अलग कर सकते हैं जिन्हें उच्च या निम्न मापा जाना है।
पिछले अध्यायों में, हमने वाल्टमीटर, एमीटर और ओममीटर के बारे में चर्चा की। इन माप उपकरणों का उपयोग क्रमशः वोल्टेज, वर्तमान और प्रतिरोध को मापने के लिए किया जाता है। इसका मतलब है, हमारे पास हैseparate measuring instruments वोल्टेज, वर्तमान और प्रतिरोध को मापने के लिए।
मान लीजिए, यदि एक बार मापने वाले उपकरण का उपयोग वोल्टेज, वर्तमान और प्रतिरोध जैसी मात्राओं को मापने के लिए किया जा सकता है, तो यह कहा जाता है multimeter। इसे मल्टीमीटर नाम मिला है, क्योंकि यह एक बार में कई विद्युत मात्राओं को माप सकता है।
मल्टीमीटर का उपयोग करके माप
Multimeterएक उपकरण है जिसका उपयोग डीसी और एसी वोल्टेज, डीसी और एसी धाराओं और कई श्रेणियों के प्रतिरोध को मापने के लिए किया जाता है। इसे इलेक्ट्रॉनिक मल्टीमीटर या वोल्टेज ओम मीटर (VOM) भी कहा जाता है।
डीसी वोल्टेज मापन
का हिस्सा है circuit diagram मल्टीमीटर, जिसका उपयोग डीसी वोल्टेज को मापने के लिए किया जा सकता है, नीचे दिए गए आंकड़े में दिखाया गया है।
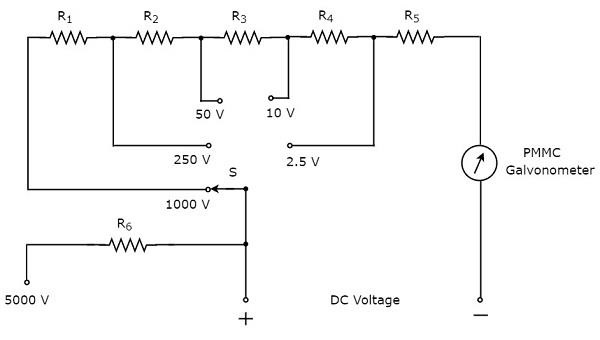
उपरोक्त सर्किट एक मल्टी रेंज डीसी वाल्टमीटर की तरह दिखता है। PMMC गैल्वेनोमीटर के साथ श्रृंखला में एक रोकनेवाला का संयोजन एक हैDC voltmeter। तो, इसका उपयोग कुछ निश्चित मूल्य तक डीसी वोल्टेज को मापने के लिए किया जा सकता है।
हम डीसी वोल्टेज की सीमा को बढ़ा सकते हैं जो प्रतिरोध मान को बढ़ाकर उसी डीसी वोल्टमीटर के साथ मापा जा सकता है। जब हम प्रतिरोधों को जोड़ते हैं तो समतुल्य प्रतिरोध मूल्य बढ़ जाता हैseries।
उपरोक्त सर्किट में, हम डीसी वोल्टेज को माप सकते हैं 2.5V रोकनेवाला के संयोजन का उपयोग करके, $R_{5}$PMMC गैल्वेनोमीटर के साथ श्रृंखला में। एक रोकनेवाला कनेक्ट करके,$R_{4}$ पिछले सर्किट के साथ श्रृंखला में, हम डीसी वोल्टेज को माप सकते हैं 10V। इस तरह, हम डीसी वोल्टेज की सीमा को बढ़ा सकते हैं, बस पिछले (पहले) सर्किट के साथ श्रृंखला में एक रोकनेवाला को जोड़कर।
हम डीसी वोल्टेज को इलेक्ट्रिक सर्किट के किसी भी दो बिंदुओं पर माप सकते हैं, स्विच से एस को वांछित वोल्टेज रेंज में जोड़कर।
डीसी वर्तमान माप
का हिस्सा है circuit diagram मल्टीमीटर, जिसका उपयोग डीसी करंट को मापने के लिए किया जा सकता है, नीचे दिए गए आंकड़े में दिखाया गया है।
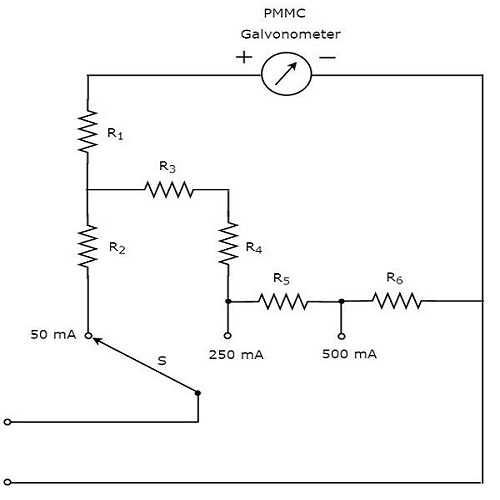
उपरोक्त सर्किट एक मल्टी रेंज डीसी एमीटर की तरह दिखता है। PMMC गैल्वेनोमीटर के समानांतर एक अवरोधक का संयोजन a हैDC ammeter। तो, इसका उपयोग निश्चित मूल्य तक डीसी धाराओं को मापने के लिए किया जा सकता है।
हम प्राप्त कर सकते हैं different rangesडीसी धाराओं को पिछले रोकनेवाला के साथ समानांतर में प्रतिरोधों को रखकर समान डीसी एमीटर के साथ मापा जाता है। ऊपर सर्किट में, रोकनेवाला,$R_{1}$ बड़ी धारा के कारण मीटर खराब होने से बचाने के लिए पीएमएमसी गैल्वेनोमीटर के साथ श्रृंखला में जुड़ा हुआ है।
हम विद्युत प्रवाह के किसी भी दो बिंदुओं के माध्यम से बहने वाले डीसी करंट को माप सकते हैं, स्विच को एस को वांछित वर्तमान सीमा से जोड़कर
एसी वोल्टेज मापन
का हिस्सा है circuit diagram मल्टीमीटर, जिसका उपयोग एसी वोल्टेज को मापने के लिए किया जा सकता है, नीचे दिए गए आंकड़े में दिखाया गया है।

उपरोक्त सर्किट एक जैसा दिखता है multi range AC voltmeter। हम जानते हैं कि, हम डीसी वाल्टमीटर के साथ श्रृंखला (कैस्केड) में रेक्टिफायर लगाकर एसी वोल्टमीटर प्राप्त करेंगे। डायोड संयोजन और अवरोधक लगाकर उपरोक्त सर्किट बनाया गया था,$R_{6}$ रोकनेवाला के बीच में, $R_{5}$ और PMMC गैल्वेनोमीटर।
हम इलेक्ट्रिक वोल्टेज के किसी भी दो बिंदुओं पर एसी वोल्टेज को माप सकते हैं, स्विच से एस को वांछित वोल्टेज रेंज से जोड़कर।
प्रतिरोध मापन
का हिस्सा है circuit diagram मल्टीमीटर का, जिसका उपयोग प्रतिरोध को मापने के लिए किया जा सकता है, नीचे दिए गए आंकड़े में दिखाया गया है।
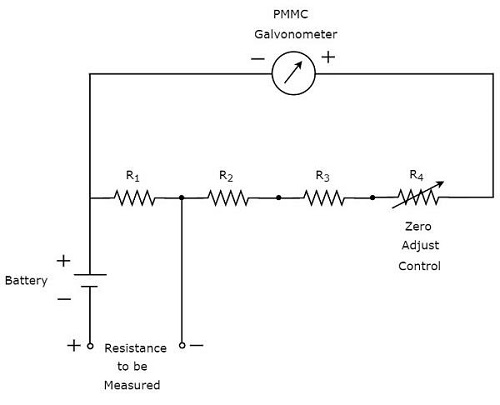
हमें कोई भी माप लेने से पहले निम्नलिखित दो कार्य करने होंगे।
- शॉर्ट सर्किट साधन
- मीटर को पूर्ण पैमाने पर करंट दिखाने तक शून्य समायोजन नियंत्रण से भिन्न करें। इसका मतलब है कि, मीटर शून्य प्रतिरोध मूल्य को इंगित करता है।
अब, उपरोक्त सर्किट शंट ओममीटर के रूप में व्यवहार करता है और इसमें 1 का स्केल गुणन होता है, अर्थात 10 0 । हम उच्च प्रतिरोधों को मापने के लिए 10 के उच्च क्रम शक्तियों को स्केल गुणकों के रूप में भी मान सकते हैं।
Signal generator एक इलेक्ट्रॉनिक उपकरण है जो साइन लहर, वर्ग तरंग, त्रिकोणीय लहर और आदि जैसे मानक परीक्षण संकेत प्रदान करता है। इसे आवधिक संकेत भी कहा जाता है, क्योंकि यह आवधिक संकेत पैदा करता है।
सिग्नल जनरेटर, जो ऑडियो फ्रीक्वेंसी (एएफ) रेंज की आवृत्ति वाले आवधिक संकेत को कहते हैं AF signal generator। ऑडियो फ्रीक्वेंसी की रेंज 20Hz से 20KHz है।
वायुसेना साइन और स्क्वायर वेव जेनरेटर
एएफ सिग्नल जनरेटर, जो आवश्यकता के आधार पर ऑडियो आवृत्तियों की सीमा में साइन तरंग या वर्ग तरंग उत्पन्न करता है, एएफ साइन और स्क्वायर वेव जनरेटर कहा जाता है। आईटी इसblock diagramनीचे दिए गए आंकड़े में दिखाया गया है।
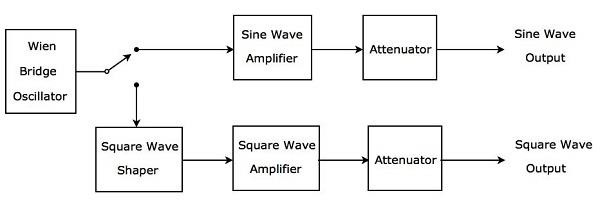
उपरोक्त ब्लॉक आरेख में मुख्य रूप से शामिल हैं two paths। वे ऊपरी रास्ते और निचले रास्ते हैं। ऊपरी पथ का उपयोग AF साइन वेव का उत्पादन करने के लिए किया जाता है और निम्न पथ का उपयोग AF वर्ग तरंग के उत्पादन के लिए किया जाता है।
Wien bridge oscillatorऑडियो आवृत्तियों की सीमा में साइन लहर पैदा करेगा। आवश्यकता के आधार पर, हम एक स्विच द्वारा वीन ब्रिज ऑसिलेटर के आउटपुट को ऊपरी पथ या निचले रास्ते से जोड़ सकते हैं।
ऊपरी पथ में साइन वेव एम्पलीफायर और एटेन्यूएटर जैसे ब्लॉक होते हैं। यदि स्विच का उपयोग ऊपरी पथ के लिए वीन ब्रिज ऑसिलेटर के आउटपुट को जोड़ने के लिए किया जाता है, तो यह एक वांछित उत्पादन करेगाAF sine wave ऊपरी पथ के आउटपुट पर।
निम्न पथ में निम्नलिखित ब्लॉक होते हैं: स्क्वायर वेव शॉपर, स्क्वायर वेव एम्पलीफायर और एटेन्यूएटर। वर्ग तरंग शेपर साइन लहर को वर्ग तरंग में परिवर्तित करता है। यदि स्विच का उपयोग वीन ब्रिज ऑसिलेटर के आउटपुट को निचले रास्ते से जोड़ने के लिए किया जाता है, तो यह एक वांछित उत्पादन करेगाAF square waveनिचले पथ के आउटपुट पर। इस तरह, जिस ब्लॉक डायग्राम को हमने माना है, उसका उपयोग आवश्यकता के आधार पर AF साइन वेव या AF स्क्वायर वेव का उत्पादन करने के लिए किया जा सकता है।
फलन जनक
फंक्शन जनरेटर एक सिग्नल जनरेटर है, जो तीन या अधिक आवधिक तरंगों को उत्पन्न करता है। निम्नलिखित को धयान मे रखते हुएblock diagram एक फंक्शन जनरेटर, जो त्रिकोणीय लहर, वर्ग तरंग और साइन लहर जैसी आवधिक लहरों का उत्पादन करेगा।
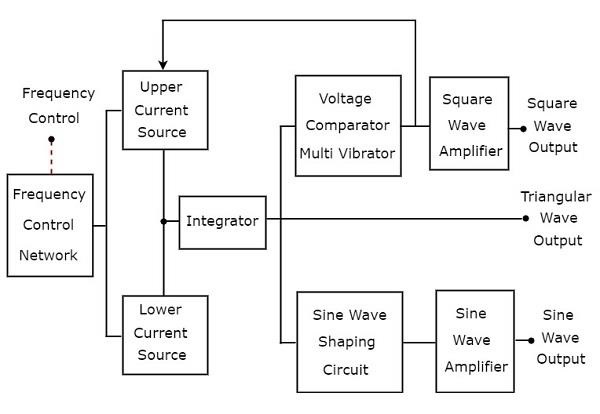
वहाँ दॊ है current sources, अर्थात् ऊपरी वर्तमान स्रोत और उपरोक्त ब्लॉक आरेख में निम्न वर्तमान स्रोत। इन दो वर्तमान स्रोतों को आवृत्ति-नियंत्रित वोल्टेज द्वारा नियंत्रित किया जाता है।
त्रिकोणीय तरंग
Integratorउपरोक्त ब्लॉक आरेख में मौजूद, ऊपरी और निचले वर्तमान स्रोतों से बारी-बारी से बराबर मात्रा में बार-बार लगातार चालू हो जाता है। इसलिए, इंटीग्रेटर एक ही समय के लिए बार-बार दो प्रकार के आउटपुट का उत्पादन करेगा -
एक इंटीग्रेटर का आउटपुट वोल्टेज increases linearly उस अवधि के लिए समय के संबंध में जिसके दौरान इंटीग्रेटर ऊपरी वर्तमान स्रोत से वर्तमान हो जाता है।
एक इंटीग्रेटर का आउटपुट वोल्टेज decreases linearly उस अवधि के लिए समय के संबंध में जिसके दौरान इंटीग्रेटर कम वर्तमान स्रोत से चालू होता है।
इस तरह, उपरोक्त ब्लॉक आरेख में मौजूद इंटीग्रेटर एक उत्पादन करेगा triangular wave।
स्क्वायर वेव और साइन वेव
इंटीग्रेटर का उत्पादन, अर्थात त्रिकोणीय लहर को दो अन्य ब्लॉकों के इनपुट के रूप में लागू किया जाता है, जैसा कि क्रमशः ब्लॉक लहर और साइन लहर को प्राप्त करने के लिए उपरोक्त ब्लॉक आरेख में दिखाया गया है। आइए एक-एक करके इन दोनों के बारे में चर्चा करें।
स्क्वेर वेव
त्रिकोणीय लहर में बार-बार समान मात्रा में बारी-बारी से सकारात्मक ढलान और नकारात्मक ढलान होता है। ऐसाvoltage comparator multi vibrator उपरोक्त ब्लॉक आरेख में मौजूद समय के बराबर मात्रा में बार-बार निम्न दो प्रकार के आउटपुट का उत्पादन करेगा।
एक प्रकार का स्थिर (higher) voltage उस अवधि के लिए वोल्टेज तुलनित्र बहु थरथानेवाला के उत्पादन में जिसके दौरान वोल्टेज तुलनित्र बहु थरथानेवाला त्रिकोणीय लहर का सकारात्मक ढलान प्राप्त करता है।
एक अन्य प्रकार की स्थिरांक (lower) voltage उस अवधि के लिए वोल्टेज तुलनित्र बहु थरथानेवाला के उत्पादन में जिसके दौरान वोल्टेज तुलनित्र बहु थरथानेवाला त्रिकोणीय तरंग की नकारात्मक ढलान प्राप्त करता है।
उपरोक्त ब्लॉक आरेख में मौजूद वोल्टेज तुलनित्र मल्टी वाइब्रेटर एक उत्पादन करेगा square wave। यदि वोल्टेज तुलनित्र मल्टी वाइब्रेटर के आउटपुट पर उत्पन्न होने वाली चौकोर तरंग का आयाम पर्याप्त नहीं है, तो इसे वर्गाकार तरंग एम्पलीफायर का उपयोग करके आवश्यक मूल्य पर बढ़ाया जा सकता है।
साइन तरंग
sine wave shaping circuitत्रिकोणीय इनपुट लहर से साइन लहर उत्पादन का उत्पादन करेगा। मूल रूप से, इस सर्किट में एक डायोड प्रतिरोध नेटवर्क होता है। यदि साइन वेव शापिंग सर्किट के आउटपुट में उत्पादित साइन वेव का आयाम अपर्याप्त है, तो इसे साइन वेव एम्पलीफायर का उपयोग करके आवश्यक मान में बढ़ाया जा सकता है।
तरंगों का विश्लेषण करने के लिए प्रयुक्त इलेक्ट्रॉनिक उपकरण को कहा जाता है wave analyzer। इसे सिग्नल एनालाइज़र भी कहा जाता है, क्योंकि शब्द सिग्नल और वेव इंटरचेंज को अक्सर इस्तेमाल किया जा सकता है।
हम प्रतिनिधित्व कर सकते हैं periodic signal निम्नलिखित दो शब्दों के योग के रूप में।
- डीसी घटक
- साइनसोइडल हार्मोनिक्स की श्रृंखला
तो, एक आवधिक संकेत का विश्लेषण इसमें प्रस्तुत हार्मोनिक्स घटकों का विश्लेषण है।
बेसिक वेव एनालाइजर
बेसिक वेव एनालाइजर में मुख्य रूप से तीन ब्लॉक होते हैं - प्राइमरी डिटेक्टर, फुल वेव रेक्टिफायर और पीएमएमसी गैल्वेनोमीटर। block diagram बेसिक वेव एनालाइजर नीचे चित्र में दिखाया गया है -
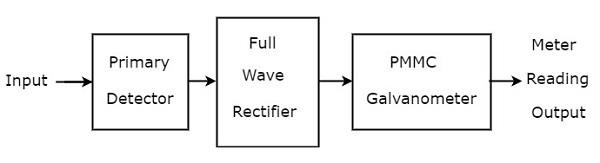
function बुनियादी तरंग विश्लेषक में मौजूद प्रत्येक ब्लॉक का उल्लेख नीचे किया गया है।
Primary Detector- इसमें एक LC सर्किट होता है। हम प्रारंभ करनेवाला, एल और संधारित्र, सी के मूल्यों को इस तरह से समायोजित कर सकते हैं कि यह केवल वांछित हार्मोनिक आवृत्ति घटक को मापता है।
Full Wave Rectifier - यह AC इनपुट को DC आउटपुट में परिवर्तित करता है।
PMMC Galvanometer - यह सिग्नल के शिखर मूल्य को दर्शाता है, जो पूर्ण लहर रेक्टिफायर के आउटपुट पर प्राप्त होता है।
हम संबंधित सर्किट आरेख को प्राप्त करेंगे, बस प्रत्येक ब्लॉक को संबंधित घटक (एस) के साथ मूल तरंग विश्लेषक के ब्लॉक ब्लॉक आरेख में बदल देंगे। ऐसाcircuit diagram बुनियादी तरंग विश्लेषक की तरह दिखेगा जैसा कि निम्न आकृति में दिखाया गया है -
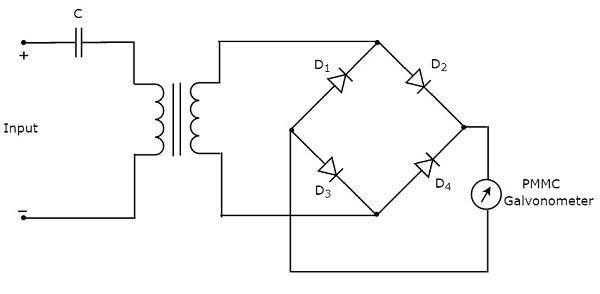
इस मूल तरंग विश्लेषक का उपयोग आवधिक संकेत के प्रत्येक हार्मोनिक आवृत्ति घटक के विश्लेषण के लिए किया जा सकता है।
वेव एनालाइजर के प्रकार
वेव एनालाइजर को निम्नलिखित में वर्गीकृत किया जा सकता है two types।
- फ़्रीक्वेंसी चयनात्मक तरंग विश्लेषक
- सुपरहीटरोडाइन वेव एनालाइजर
अब, इन दो तरंग विश्लेषणों के बारे में एक-एक करके चर्चा करते हैं।
फ़्रीक्वेंसी चयनात्मक तरंग विश्लेषक
सिग्नल के विश्लेषण के लिए उपयोग किए जाने वाले वेव एनालाइजर को एएफ रेंज के होते हैं, जिसे फ़्रीक्वेंसी सेलेक्टिव वेव एनालाइज़र कहा जाता है। block diagram आवृत्ति चयनात्मक तरंग विश्लेषक नीचे दिए गए आंकड़े में दिखाया गया है।
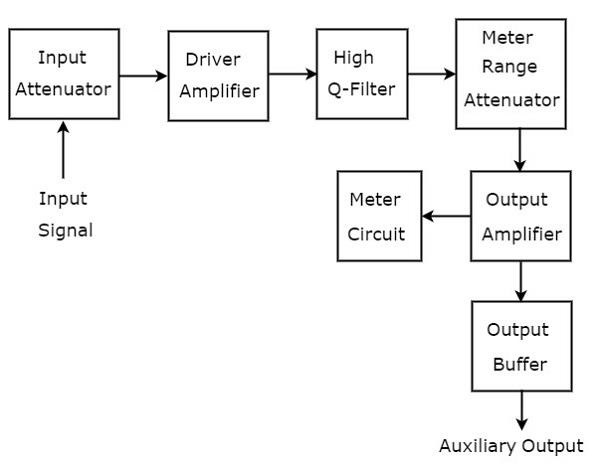
फ़्रीक्वेंसी चयनात्मक तरंग विश्लेषक में ब्लॉकों का एक सेट होता है। function प्रत्येक ब्लॉक का उल्लेख नीचे किया गया है।
Input Attenuator- एएफ सिग्नल, जिसका विश्लेषण किया जाना है, इनपुट एटेन्यूएटर पर लागू होता है। यदि सिग्नल का आयाम बहुत बड़ा है, तो इसे इनपुट एटेन्यूएटर द्वारा देखा जा सकता है।
Driver Amplifier - यह जब भी आवश्यक हो प्राप्त संकेत को बढ़ाता है।
High Q-filter- इसका उपयोग वांछित आवृत्ति का चयन करने और अवांछित आवृत्तियों को अस्वीकार करने के लिए किया जाता है। इसमें दो RC खंड और दो फ़िल्टर एम्पलीफायर्स होते हैं और इन सभी को एक दूसरे के साथ कैस्केड किया जाता है। हम 10. की शक्तियों में आवृत्तियों की सीमा को बदलने के लिए समाई मूल्यों को भिन्न कर सकते हैं। इसी प्रकार, हम चयनित रेंज के भीतर आवृत्ति को बदलने के लिए प्रतिरोध मानों को भिन्न कर सकते हैं।
Meter Range Attenuator - इसे इनपुट के रूप में चयनित AF सिग्नल मिलता है और जब भी आवश्यकता होती है, एक आउटपुट का उत्पादन होता है।
Output Amplifier - यदि आवश्यक हो तो यह चयनित वायुसेना संकेत को बढ़ाता है।
Output Buffer - इसका उपयोग आउटपुट डिवाइसों को चयनित AF सिग्नल प्रदान करने के लिए किया जाता है।
Meter Circuit- यह चयनित वायुसेना संकेत के पढ़ने को प्रदर्शित करता है। हम मीटर रीडिंग को वोल्ट रेंज या डेसीबल रेंज में चुन सकते हैं।
सुपरहीटरोडाइन वेव एनालाइजर
आरएफ रेंज के संकेतों का विश्लेषण करने के लिए उपयोग किए जाने वाले तरंग विश्लेषक को सुपरहीटरोडाइन तरंग विश्लेषक कहा जाता है। निम्नलिखित आंकड़ा दिखाता हैblock diagram सुपरहीटरोडाइन वेव एनालाइजर का।
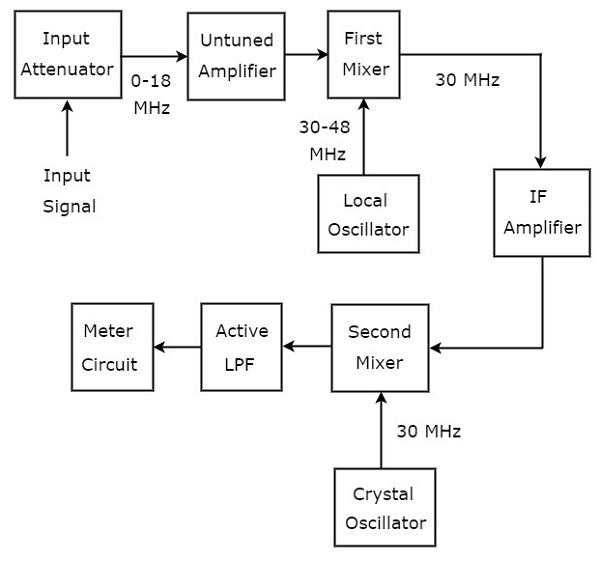
working सुपरहीटरोडाइन वेव एनालाइजर का उल्लेख नीचे किया गया है।
आरएफ सिग्नल, जिसका विश्लेषण किया जाना है, इनपुट एटेन्यूएटर पर लागू होता है। यदि सिग्नल का आयाम बहुत बड़ा है, तो इसे द्वारा देखा जा सकता हैinput attenuator।
Untuned amplifier जब भी आवश्यक हो आरएफ सिग्नल को बढ़ाता है और इसे पहले मिक्सर पर लागू किया जाता है।
स्थानीय सिग्नल थरथरानवाला के आरएफ सिग्नल और आउटपुट की आवृत्ति रेंज क्रमशः 0-18 मेगाहर्ट्ज और 30-48 मेगाहर्ट्ज है। इसलिए,first mixerएक आउटपुट पैदा करता है, जिसमें 30 MHz की आवृत्ति होती है। यह उस पर लागू होने वाले दो संकेतों की आवृत्तियों का अंतर है।
IF amplifierइंटरमीडिएट फ़्रीक्वेंसी (IF) सिग्नल को बढ़ाता है, यानी पहले मिक्सर का आउटपुट। प्रवर्धित IF सिग्नल को दूसरे मिक्सर पर लागू किया जाता है।
प्रवर्धित IF सिग्नल और क्रिस्टल थरथरानवाला के उत्पादन की आवृत्ति समान और 30MHz के बराबर होती है। ऐसाsecond mixerएक आउटपुट उत्पन्न करता है, जिसमें 0 हर्ट्ज की आवृत्ति होती है। यह उस पर लागू होने वाले दो संकेतों की आवृत्तियों का अंतर है।
की कट ऑफ फ्रीक्वेंसी Active Low Pass Filter (LPF)1500 हर्ट्ज के रूप में चुना गया है। इसलिए, यह फ़िल्टर दूसरे मिक्सर के आउटपुट सिग्नल की अनुमति देता है।
Meter Circuitआरएफ संकेत के पढ़ने को प्रदर्शित करता है। हम मीटर रीडिंग को वोल्ट रेंज या डेसीबल रेंज में चुन सकते हैं।
इसलिए, हम सिग्नल की आवृत्ति रेंज के आधार पर एक विशेष तरंग विश्लेषक चुन सकते हैं जिसका विश्लेषण किया जाना है।
इलेक्ट्रॉनिक उपकरण, जिसका उपयोग आवृत्ति डोमेन में तरंगों के विश्लेषण के लिए किया जाता है spectrum analyzer। मूल रूप से, यह अपने CRT स्क्रीन पर एक सिग्नल के ऊर्जा वितरण को प्रदर्शित करता है। यहाँ, x- अक्ष आवृत्ति का प्रतिनिधित्व करता है और y- अक्ष आयाम का प्रतिनिधित्व करता है।
स्पेक्ट्रम एनालाइजर के प्रकार
हम निम्नलिखित में स्पेक्ट्रम विश्लेषणकर्ताओं को वर्गीकृत कर सकते हैं two types।
- फ़िल्टर बैंक स्पेक्ट्रम विश्लेषक
- सुपरहीटरोडाइन स्पेक्ट्रम विश्लेषक
अब, हम एक-एक करके इन दोनों स्पेक्ट्रम विश्लेषणकर्ताओं के बारे में चर्चा करते हैं।
फ़िल्टर बैंक स्पेक्ट्रम विश्लेषक
स्पेक्ट्रम विश्लेषक, जो संकेतों के विश्लेषण के लिए उपयोग किए जाते हैं, AF रेंज के होते हैं, जिन्हें फ़िल्टर बैंक स्पेक्ट्रम विश्लेषक कहा जाता है, या real time spectrum analyzer क्योंकि यह सभी इनपुट आवृत्तियों में किसी भी भिन्नता को दिखाता (दिखाता) है।
निम्नलिखित आंकड़ा दिखाता है block diagram फ़िल्टर बैंक स्पेक्ट्रम विश्लेषक का।
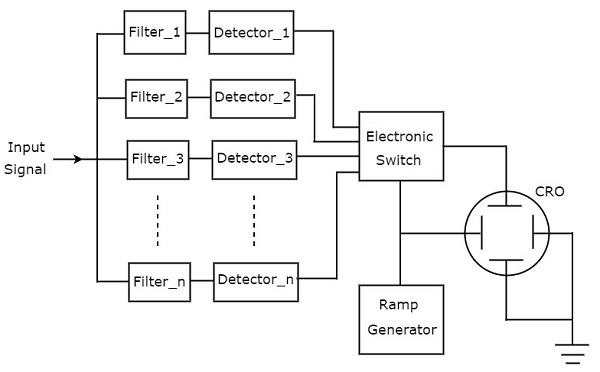
working फ़िल्टर बैंक स्पेक्ट्रम विश्लेषक नीचे उल्लिखित है।
इसमें बैंड पास फिल्टर का एक सेट है और प्रत्येक को विशिष्ट बैंड के आवृत्तियों की अनुमति देने के लिए डिज़ाइन किया गया है। प्रत्येक बैंड पास फिल्टर का आउटपुट संबंधित डिटेक्टर को दिया जाता है।
सभी डिटेक्टर आउटपुट इलेक्ट्रॉनिक स्विच से जुड़े हैं। यह स्विच डिटेक्टर आउटपुट को क्रॉप के वर्टिकल डिफ्लेशन प्लेट में क्रमिक रूप से अनुमति देता है। तो, सीआरओ आवृत्ति प्रदर्शित करता हैspectrum of AF signal इसकी CRT स्क्रीन पर।
सुपरहीटरोडाइन स्पेक्ट्रम विश्लेषक
स्पेक्ट्रम विश्लेषक, जो संकेतों के विश्लेषण के लिए उपयोग किया जाता है, आरएफ रेंज के होते हैं superheterodyne spectrum analyzer। आईटी इसblock diagram नीचे दिए गए आंकड़े में दिखाया गया है।
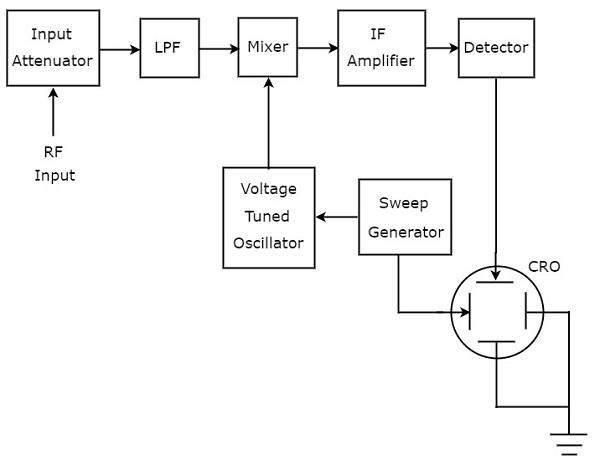
working सुपरथेरोडाइन स्पेक्ट्रम विश्लेषक का उल्लेख नीचे किया गया है।
आरएफ सिग्नल, जिसका विश्लेषण किया जाना है, इनपुट एटेन्यूएटर पर लागू होता है। यदि सिग्नल का आयाम बहुत बड़ा है, तो इसे ए द्वारा देखा जा सकता हैinput attenuator।
Low Pass Filter (एलपीएफ) केवल आवृत्ति घटकों की अनुमति देता है जो कट-ऑफ आवृत्ति से कम हैं।
Mixerलो पास फिल्टर और वोल्टेज ट्यून्ड ऑसिलेटर से इनपुट मिलते हैं। यह एक आउटपुट का उत्पादन करता है, जो उस पर लागू होने वाले दो संकेतों की आवृत्तियों का अंतर है।
IF amplifierइंटरमीडिएट फ्रिक्वेंसी (IF) सिग्नल, यानी मिक्सर का आउटपुट बढ़ाता है। प्रवर्धित IF सिग्नल डिटेक्टर पर लागू होता है।
डिटेक्टर का आउटपुट सीआरओ के ऊर्ध्वाधर विक्षेपन प्लेट को दिया जाता है। तो, सीआरओ आवृत्ति प्रदर्शित करता हैspectrum of RF signal इसकी CRT स्क्रीन पर।
तो, हम एक विशेष स्पेक्ट्रम विश्लेषक चुन सकते हैं जो सिग्नल की आवृत्ति रेंज के आधार पर विश्लेषण किया जाना है।
Oscilloscopeएक इलेक्ट्रॉनिक उपकरण है, जो एक वोल्टेज तरंग प्रदर्शित करता है। ऑसिलोस्कोप के बीच, कैथोड रे ओसिलोस्कोप (सीआरओ) मूल एक है और यह एक समय बदलती संकेत या तरंग प्रदर्शित करता है।
इस अध्याय में, हम सीआरओ के ब्लॉक आरेख और सीआरओ का उपयोग करके कुछ मापदंडों के माप के बारे में चर्चा करते हैं।
सीआरओ के ब्लॉक आरेख
कैथोड रे ओसिलोस्कोप (सीआरओ) में ब्लॉक का एक सेट होता है। वे ऊर्ध्वाधर एम्पलीफायर, देरी लाइन, ट्रिगर सर्किट, टाइम बेस जनरेटर, क्षैतिज एम्पलीफायर, कैथोड रे ट्यूब (सीआरटी) और बिजली की आपूर्ति हैं। block diagram सीआरओ नीचे दिए गए आंकड़े में दिखाया गया है।
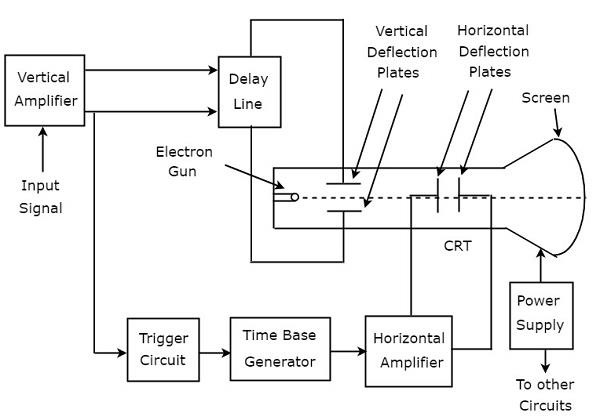
function सीआरओ के प्रत्येक ब्लॉक का उल्लेख नीचे किया गया है।
Vertical Amplifier - यह इनपुट सिग्नल को बढ़ाता है, जिसे CRT की स्क्रीन पर प्रदर्शित किया जाना है।
Delay Line- यह सिग्नल को कुछ देरी प्रदान करता है, जो ऊर्ध्वाधर एम्पलीफायर के आउटपुट में प्राप्त होता है। यह विलंबित संकेत तब CRT के लंबवत विक्षेपण प्लेटों पर लागू होता है।
Trigger Circuit - यह इलेक्ट्रॉन बीम के क्षैतिज और ऊर्ध्वाधर दोनों विक्षेपों को सिंक्रनाइज़ करने के लिए एक ट्रिगर सिग्नल का उत्पादन करता है।
Time base Generator - यह एक sawtooth संकेत पैदा करता है, जो इलेक्ट्रॉन बीम के क्षैतिज विक्षेपन के लिए उपयोगी है।
Horizontal Amplifier - यह sawtooth सिग्नल को बढ़ाता है और फिर इसे CRT के क्षैतिज विक्षेपण प्लेटों से जोड़ता है।
Power supply- यह उच्च और निम्न दोनों वोल्टेज का उत्पादन करता है। नकारात्मक उच्च वोल्टेज और सकारात्मक कम वोल्टेज क्रमशः सीआरटी और अन्य सर्किट पर लागू होते हैं।
Cathode Ray Tube (CRT)- यह सीआरओ का प्रमुख महत्वपूर्ण ब्लॉक है और इसमें मुख्य रूप से चार भाग होते हैं। वे इलेक्ट्रॉन बंदूक, ऊर्ध्वाधर विक्षेपण प्लेट, क्षैतिज विक्षेपण प्लेट और फ्लोरोसेंट स्क्रीन हैं।
इलेक्ट्रॉन बीम, जो एक इलेक्ट्रॉन बंदूक द्वारा निर्मित होती है, ऊर्ध्वाधर ऊर्ध्वाधर और क्षैतिज दिशाओं में क्रमशः ऊर्ध्वाधर विक्षेपण प्लेटों की एक जोड़ी और क्षैतिज विक्षेपन प्लेटों की एक जोड़ी द्वारा विक्षेपित हो जाती है। अंत में, विक्षेपित बीम फ्लोरोसेंट स्क्रीन पर एक स्पॉट के रूप में दिखाई देगा।
इस तरह, सीआरओ सीआरटी के स्क्रीन पर लागू इनपुट सिग्नल को प्रदर्शित करेगा। इसलिए, हम सीआरओ का उपयोग करके समय डोमेन में संकेतों का विश्लेषण कर सकते हैं
सीआरओ का उपयोग करके माप
हम सीआरओ का उपयोग करके निम्नलिखित माप कर सकते हैं।
- आयाम का मापन
- समय अवधि का मापन
- आवृत्ति का मापन
अब, इन मापों के बारे में एक-एक करके चर्चा करते हैं।
आयाम का मापन
सीआरओ अपनी स्क्रीन पर समय के एक समारोह के रूप में वोल्टेज संकेत प्रदर्शित करता है। amplitude कि वोल्टेज सिग्नल स्थिर है, लेकिन हम उन विभाजनों की संख्या को अलग-अलग कर सकते हैं जो वोल्टेज सिग्नल को अलग-अलग करके ऊर्ध्वाधर दिशा में कवर करते हैं volt/divisionसीआरओ पैनल पर घुंडी। इसलिए, हम प्राप्त करेंगेamplitude सिग्नल, जो निम्नलिखित सूत्र का उपयोग करके सीआरओ की स्क्रीन पर मौजूद है।
$$A=j\times n_{v}$$
कहाँ पे,
$A$ आयाम है
$j$ वोल्ट / विभाजन का मान है
$n_{v}$ ऊर्ध्वाधर दिशाओं में सिग्नल को कवर करने वाले डिवीजनों की संख्या है।
समय अवधि का मापन
सीआरओ अपनी स्क्रीन पर समय के एक समारोह के रूप में वोल्टेज संकेत प्रदर्शित करता है। Time period उस आवधिक वोल्टेज संकेत की निरंतरता है, लेकिन हम उन विभाजनों की संख्या को अलग-अलग कर सकते हैं जो अलग-अलग होकर क्षैतिज दिशा में वोल्टेज संकेत के एक पूर्ण चक्र को कवर करते हैं time/division सीआरओ पैनल पर घुंडी।
इसलिए, हम प्राप्त करेंगे Time period सिग्नल, जो निम्नलिखित सूत्र का उपयोग करके सीआरओ की स्क्रीन पर मौजूद है।
$$T=k\times n_{h}$$
कहाँ पे,
$T$ समय अवधि है
$j$ समय / विभाजन का मूल्य है
$n_{v}$ विभाजनों की संख्या है जो क्षैतिज दिशा में आवधिक संकेत के एक पूर्ण चक्र को कवर करती है।
आवृत्ति का मापन
आवधिक सिग्नल की आवृत्ति, एफ, समय अवधि का पारस्परिक है, टी। Mathematically, यह के रूप में प्रतिनिधित्व किया जा सकता है
$$f=\frac{1}{T}$$
तो, हम इन दो चरणों का पालन करके आवधिक संकेत के आवृत्ति, एफ पा सकते हैं।
Step1 - खोजें Time period आवधिक संकेत
Step2 - ले लो reciprocal समय-समय पर संकेत की अवधि, जो चरण 1 में प्राप्त की जाती है
हम अगले अध्याय में विशेष उद्देश्य आस्टसीलस्कॉप के बारे में चर्चा करेंगे।
पिछले अध्याय में, हमने कैथोड रे ओसिलोस्कोप (सीआरओ) के बारे में चर्चा की थी, जो एक बुनियादी आस्टसीलस्कप है। हमें आवश्यकता के आधार पर बुनियादी आस्टसीलस्कप के कुछ अतिरिक्त ब्लॉकों को शामिल करके विशेष प्रयोजन के आस्टसीलस्कॉप प्राप्त होंगे।
निम्नलिखित हैं special purpose oscilloscopes।
- दोहरी बीम ओस्सिलोस्कोप
- डुअल ट्रेस ऑसिलोस्कोप
- डिजिटल स्टोरेज ऑसिलोस्कोप
अब, आइए हम एक-एक करके इन विशेष प्रयोजन के दोलन के बारे में चर्चा करें।
दोहरी बीम ओस्सिलोस्कोप
Oscilloscope, जो दो वोल्टेज तरंगों को प्रदर्शित करता है, को ड्यूल बीम Oscilloscope कहते हैं। आईटी इसblock diagram नीचे दिए गए आंकड़े में दिखाया गया है।
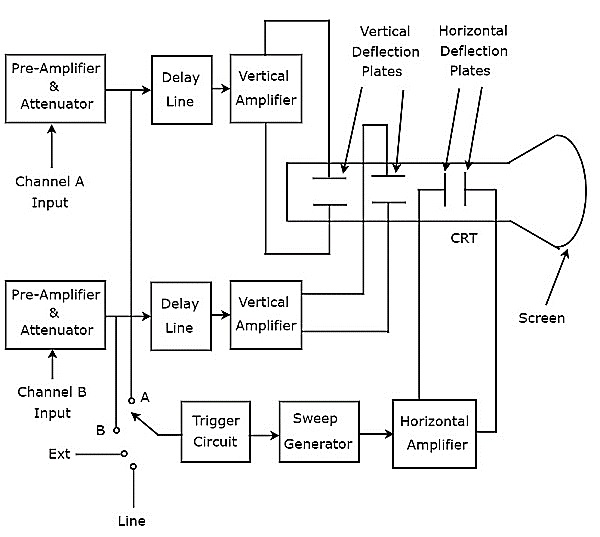
जैसा कि ऊपर की आकृति में दिखाया गया है, दोहरी बीम ऑसिलोस्कोप के सीआरटी में ऊर्ध्वाधर विक्षेपण प्लेटों के दो सेट और क्षैतिज विक्षेपण प्लेटों के एक सेट होते हैं।
निम्नलिखित ब्लॉकों के संयोजन को एक साथ कहा जाता है channel।
- पूर्व एम्पलीफायर और Attenuator
- विलंब रेखा
- ऊर्ध्वाधर एम्पलीफायर
- ऊर्ध्वाधर विक्षेपण प्लेटों का एक सेट
डुअल बीम ऑसिलोस्कोप में दो चैनल हैं। तो, हम दो संकेतों को क्रमशः ए और बी चैनल ए और चैनल बी के इनपुट के रूप में लागू कर सकते हैं। हम इन चार संकेतों में से किसी एक को चुन सकते हैंtrigger inputएक स्विच का उपयोग करके ट्रिगर सर्किट को। वे इनपुट सिग्नल ए एंड बी, बाहरी सिग्नल (एक्सट) और लाइन इनपुट हैं।
यह आस्टसीलस्कप दो लंबवत विक्षेपित बीमों का उत्पादन करेगा, क्योंकि ऊर्ध्वाधर विक्षेपण प्लेटों के दो जोड़े हैं। इस आस्टसीलस्कप में, बीम जो क्षैतिज दिशा में विक्षेपित करने के लिए उपयोगी होते हैं, दोनों इनपुट संकेतों के लिए सामान्य है। अंत में, यह आस्टसीलस्कप का उत्पादन करेगाtwo input signals एक साथ CRT की स्क्रीन पर।
डुअल ट्रेस ऑसिलोस्कोप
Oscilloscope, जो अपनी स्क्रीन पर दो निशान पैदा करता है, को Dual Trace Oscilloscope कहते हैं। आईटी इसblock diagram नीचे दिए गए आंकड़े में दिखाया गया है।
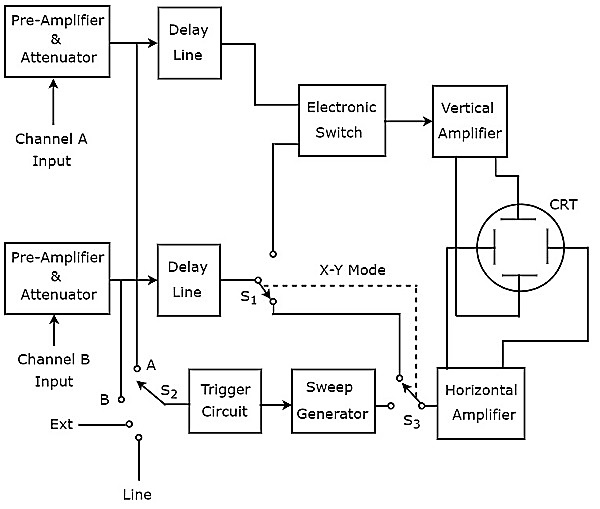
जैसा कि ऊपर की आकृति में दिखाया गया है, दोहरे ट्रेस ऑसिलोस्कोप के सीआरटी में ऊर्ध्वाधर विक्षेपण प्लेटों का एक सेट और क्षैतिज विक्षेपण प्लेटों का एक और सेट होता है। चैनल में चार ब्लॉक होते हैं, यानी प्री-एम्पलीफायर और एटेन्यूएटर, विलंब रेखा, ऊर्ध्वाधर एम्पलीफायर और ऊर्ध्वाधर विक्षेपण प्लेट।
उपरोक्त ब्लॉक आरेख में, पहले दो ब्लॉक दोनों चैनलों में अलग-अलग मौजूद हैं। अंतिम दो ब्लॉक दोनों चैनलों के लिए आम हैं। इसलिए, की मदद सेelectronic switch हम एक विशिष्ट चैनल के विलंब रेखा आउटपुट को ऊर्ध्वाधर एम्पलीफायर से जोड़ सकते हैं।
हम इन चार संकेतों में से किसी एक को ट्रिगर इनपुट के रूप में चुन सकते हैं trigger circuitएक स्विच का उपयोग करके। वे इनपुट सिग्नल ए एंड बी, बाहरी सिग्नल (एक्सट) और लाइन इनपुट हैं।
यह ऑसिलोस्कोप इलेक्ट्रॉनिक स्विच का उपयोग करके ऊर्ध्वाधर दिशा में इनपुट संकेतों ए एंड बी को विक्षेपित करने के लिए एक ही इलेक्ट्रॉन बीम का उपयोग करता है, और उत्पादन करता है two traces। ब्लॉक जो क्षैतिज रूप से बीम को डिफ्लेक्ट करते हैं, दोनों इनपुट सिग्नल के लिए सामान्य है।
डिजिटल स्टोरेज ऑसिलोस्कोप
आस्टसीलस्कप, जो तरंग को डिजिटल रूप से संग्रहीत करता है, डिजिटल भंडारण आस्टसीलस्कप के रूप में जाना जाता है। block diagram (डिजिटल) भंडारण आस्टसीलस्कप नीचे है -
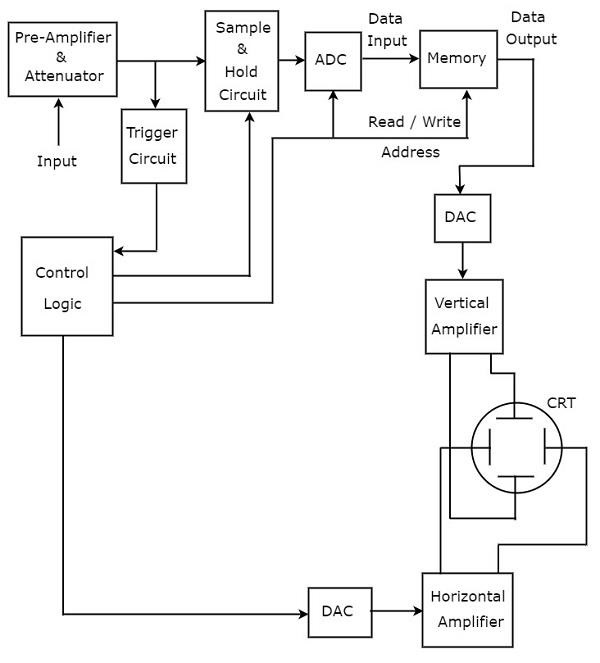
डिजिटल डेटा स्टोरेज के लिए आवश्यक अतिरिक्त ब्लॉक को एक बुनियादी ऑसिलोस्कोप में जोड़ा जाता है ताकि इसे डिजिटल स्टोरेज ऑसिलोस्कोप में परिवर्तित किया जा सके। जिन ब्लॉकों की आवश्यकता हैstoring of digital dataप्री-एम्पलीफायर और एटेन्यूएटर और डिजिटल स्टोरेज ऑसिलोस्कोप में ऊर्ध्वाधर एम्पलीफायर के बीच स्थित है। वे नमूना और होल्ड सर्किट, एनालॉग से डिजिटल कनवर्टर (एडीसी), मेमोरी और डिजिटल से एनालॉग कनवर्टर हैं।
Control logicविभिन्न नियंत्रण संकेतों को भेजकर पहले तीन ब्लॉकों को नियंत्रित करता है। कंट्रोल लॉजिक और डिजिटल से एनालॉग कनवर्टर जैसे ब्लॉक ट्रिगर सर्किट और डिजिटल स्टोरेज ऑस्सिलोस्कोप में क्षैतिज एम्पलीफायर के बीच मौजूद हैं।
डिजिटल स्टोरेज ऑसिलोस्कोप stores the dataडिजिटल में यह स्क्रीन पर तरंग प्रदर्शित करता है। जबकि, बुनियादी आस्टसीलस्कप में यह सुविधा नहीं होती है।
Lissajous figureपैटर्न है जो स्क्रीन पर प्रदर्शित किया जाता है, जब साइनसॉइडल सिग्नल सीआरओ के क्षैतिज और ऊर्ध्वाधर विक्षेपण प्लेटों पर लागू होते हैं। ये पैटर्न साइनसॉइडल संकेतों के आयाम, आवृत्तियों और चरण अंतर के आधार पर भिन्न होंगे, जो सीआरओ के दोनों क्षैतिज और ऊर्ध्वाधर विक्षेपण प्लेटों पर लागू होते हैं।
निम्नलिखित आंकड़ा एक दिखाता है example लिज्जत की आकृति।
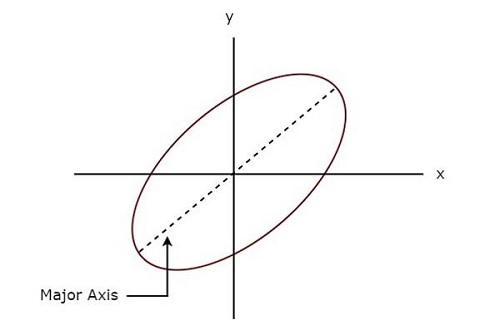
उपरोक्त लिसाझोस आकृति में है elliptical shape और इसके प्रमुख अक्ष में सकारात्मक एक्स-अक्ष के साथ कुछ झुकाव कोण है।
Lissajous आंकड़े का उपयोग कर माप
हम निम्नलिखित कर सकते हैं two measurements एक Lissajous फिगर से।
- साइनसोइडल सिग्नल की आवृत्ति
- दो साइनसोइडल संकेतों के बीच चरण अंतर
अब, हम एक-एक करके इन दो मापों के बारे में चर्चा करते हैं।
आवृत्ति का मापन
स्क्रीन पर Lissajous आंकड़ा प्रदर्शित किया जाएगा, जब साइनसॉइडल सिग्नल सीआरओ के क्षैतिज और ऊर्ध्वाधर विक्षेपण प्लेटों पर लागू होते हैं। इसलिए, साइनसोइडल सिग्नल लागू करें, जिसमें मानक हैknown frequencyसीआरओ के क्षैतिज विक्षेपन प्लेटों के लिए। इसी तरह, साइनसोइडल सिग्नल को लागू करें, जिसकाfrequency है unknown सीआरओ के ऊर्ध्वाधर विक्षेपन प्लेटों के लिए
चलो, $f_{H}$ तथा $f_{V}$साइनसोइडल सिग्नल की आवृत्तियों हैं, जो क्रमशः सीआरओ के क्षैतिज और ऊर्ध्वाधर विक्षेपण प्लेटों पर लागू होती हैं। बीच के रिश्ते$f_{H}$ तथा $f_{V}$ हो सकता है mathematically नीचे के रूप में प्रतिनिधित्व किया।
$$\frac{f_{V}}{f_{H}}=\frac{n_{H}}{n_{V}}$$
उपरोक्त संबंध से, हम साइनसोइडल सिग्नल की आवृत्ति प्राप्त करेंगे, जो सीआरओ के ऊर्ध्वाधर विक्षेपन प्लेटों पर लागू होता है
$f_{V}=\left ( \frac{n_{H}}{n_{V}} \right )f_{H}$(समीकरण 1)
कहाँ पे,
$n_{H}$ क्षैतिज स्पर्शरेखाओं की संख्या है
$n_{V}$ ऊर्ध्वाधर स्पर्शरेखाओं की संख्या है
हम के मूल्यों को पा सकते हैं $n_{H}$ तथा $n_{V}$लिज्जत आकृति से। तो, के मूल्यों को प्रतिस्थापित करके$n_{H}$, $n_{V}$ तथा $f_{H}$ समीकरण 1 में, हमें इसका मान मिलेगा $f_{V}$, यानी frequency of sinusoidal signal कि सीआरओ के ऊर्ध्वाधर विक्षेपन प्लेटों पर लागू होता है।
चरण अंतर का मापन
जब स्क्रीन पर साइनसॉइडल सिग्नल सीआरओ के क्षैतिज और ऊर्ध्वाधर विक्षेपण प्लेटों पर लागू होते हैं, तो एक लेज़ाजस आकृति प्रदर्शित की जाती है। इसलिए, साइनसोइडल संकेतों को लागू करें, जिनके पास हैsame amplitude and frequency सीआरओ के दोनों क्षैतिज और ऊर्ध्वाधर विक्षेपन प्लेटों के लिए।
उनके आकार के आधार पर कुछ लिसाजस आंकड़ों के लिए, हम सीधे दो साइनसोइडल संकेतों के बीच चरण अंतर बता सकते हैं।
यदि लिज्जाज आकृति एक है straight line के झुकाव के साथ $45^{\circ}$ सकारात्मक एक्स-अक्ष के साथ, फिर phase difference दो साइनसोइडल संकेतों के बीच होगा $0^{\circ}$। इसका मतलब है, उन दो साइनसोइडल संकेतों के बीच कोई चरण अंतर नहीं है।
यदि लिज्जाज आकृति एक है straight line के झुकाव के साथ $135^{\circ}$ सकारात्मक एक्स-अक्ष के साथ, फिर phase difference दो साइनसोइडल संकेतों के बीच होगा $180^{\circ}$। इसका मतलब है, वे दो साइनसोइडल सिग्नल चरण से बाहर हैं।
अगर लिसजोस फिगर में है circular shape, तो दो साइनसोइडल संकेतों के बीच चरण अंतर होगा $90^{\circ}$ या $270^{\circ}$।
जब Lissajous आंकड़े होते हैं, तो हम सूत्रों का उपयोग करके दो साइनसोइडल संकेतों के बीच चरण अंतर की गणना कर सकते हैं elliptical shape।
यदि एक अण्डाकार आकृति की प्रमुख धुरी लिज्जाज आकृति का झुकाव कोण होता है $0^{\circ}$ तथा $90^{\circ}$ सकारात्मक एक्स-अक्ष के साथ, फिर दो साइनसोइडल संकेतों के बीच चरण अंतर होगा।
$$\phi =\sin ^{-1}\left ( \frac{x_{1}}{x_{2}} \right )=\sin ^{-1}\left ( \frac{y_{1}}{y_{2}} \right )$$
यदि एक अण्डाकार आकृति की प्रमुख धुरी लिज्जाज आकृति का झुकाव कोण होता है $90^{\circ}$ तथा $180^{\circ}$ सकारात्मक एक्स-अक्ष के साथ, फिर दो साइनसोइडल संकेतों के बीच चरण अंतर होगा।
$$\phi =180 - \sin ^{-1}\left ( \frac{x_{1}}{x_{2}} \right )=180 - \sin ^{-1}\left ( \frac{y_{1}}{y_{2}} \right )$$
Where,
$x_{1}$ एक्स-अक्ष पर मूल से बिंदु तक की दूरी है, जहां अण्डाकार आकृति लिसाझोस आकृति अंतर करती है
$x_{2}$ मूल से दीर्घवृत्ताकार आकृति के लंबवत स्पर्शरेखा की दूरी है
$y_{1}$ y- अक्ष पर मूल से बिंदु की दूरी है, जहां अण्डाकार आकृति लिसाझोस आकृति को काटती है
$y_{2}$ मूल से अण्डाकार आकृति के क्षैतिज स्पर्शरेखा की दूरी है Lissajous आंकड़ा
इस अध्याय में, अज्ञात साइनसोइडल सिग्नल की आवृत्ति का पता लगाना और सूत्रों के उपयोग से लिसाजस आंकड़ों से दो साइनसोइडल संकेतों के बीच के अंतर का पता लगाना।
हम एक जांच के माध्यम से किसी भी परीक्षण सर्किट को आस्टसीलस्कप से जोड़ सकते हैं। जैसा कि सीआरओ एक बुनियादी आस्टसीलस्कप है, जो जांच से जुड़ा है उसे भी कहा जाता हैCRO probe।
हमें जांच का चयन इस तरह से करना चाहिए कि यह परीक्षण सर्किट के साथ कोई लोडिंग समस्या पैदा न करे। ताकि हम सीआरओ स्क्रीन पर संकेतों के साथ परीक्षण सर्किट का ठीक से विश्लेषण कर सकें।
सीआरओ जांच में निम्नलिखित होना चाहिए characteristics।
- कड़ा मुकाबला
- उच्च बैंडविड्थ
block diagram सीआरओ जांच नीचे दिए गए आंकड़े में दिखाई गई है।
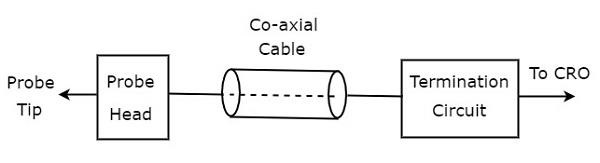
जैसा कि चित्र में दिखाया गया है, सीआरओ जांच में मुख्य रूप से तीन ब्लॉक होते हैं। वे जांच प्रमुख, सह-अक्षीय केबल और समाप्ति सर्किट हैं। सह-अक्षीय केबल बस जांच सिर और समाप्ति सर्किट को जोड़ता है।
सीआरओ प्रोब के प्रकार
सीआरओ जांच को निम्नलिखित में वर्गीकृत किया जा सकता है two types।
- निष्क्रिय जांच
- सक्रिय जांच
अब, आइए एक-एक करके इन दो प्रकार की जांचों के बारे में चर्चा करें।
निष्क्रिय जांच
यदि जांच सिर में निष्क्रिय तत्व होते हैं, तो इसे कहा जाता है passive probe। निष्क्रिय जांच का सर्किट आरेख नीचे दिए गए आंकड़े में दिखाया गया है।
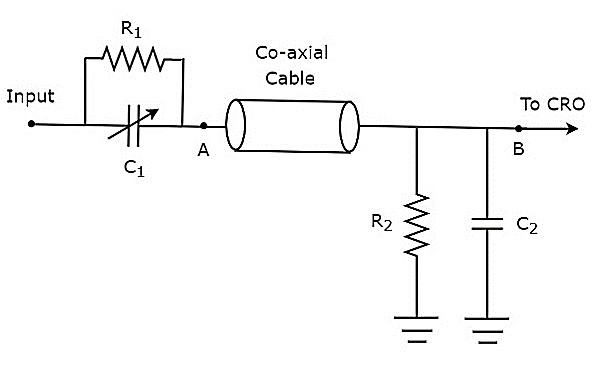
जैसा कि चित्र में दिखाया गया है, जांच सिर में रोकनेवाला के समानांतर संयोजन होता है, $R_{1}$ और एक चर संधारित्र, $C_{1}$। इसी तरह, समाप्ति सर्किट में रोकनेवाला के समानांतर संयोजन होता है,$R_{2}$ और संधारित्र, $C_{2}$।
उपरोक्त सर्किट आरेख के रूप में संशोधित किया गया है bridge circuit और यह नीचे दिए गए आंकड़े में दिखाया गया है।
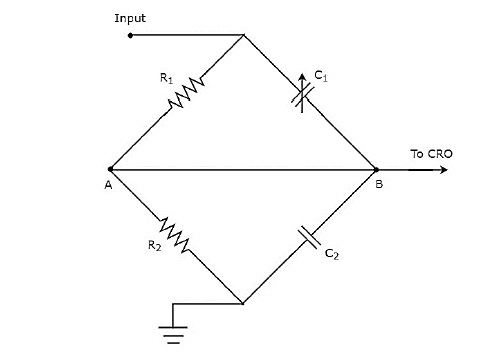
हम चर संधारित्र के मान को समायोजित करके पुल को संतुलित कर सकते हैं, $c_{1}$। हम निम्नलिखित अध्यायों में पुलों की अवधारणा पर चर्चा करेंगे। कुछ समय के लिए, निम्नलिखित पर विचार करेंbalancing condition of AC bridge।
$$Z_{1}Z_{4}=Z_{2}Z_{3}$$
Substitute, बाधाएं $Z_{1},Z_{2}, Z_{3}$ तथा $Z_{4}$ जैसा $R_{1},\frac{1}{j\omega C_{1}}, R_{2}$ तथा $\frac{1}{j\omega C_{2}}$ क्रमशः उपरोक्त समीकरण में।
$$R_{1}\left ( \frac{1}{j \omega C_{2}} \right )=\left ( \frac{1}{j \omega C_{1}} \right )R_{2}$$
$\Rightarrow R_{1} C_{1}=R_{2} C_{2}$समीकरण 1
वोल्टेज डिवीजन सिद्धांत द्वारा, हम प्राप्त करेंगे voltage across resistor, $R_{2}$ जैसा
$$V_{0}=V_{i}\left ( \frac{R_{2}}{R_{1}+R_{2}} \right )$$
attenuation factor इनपुट वोल्टेज का अनुपात है, $V_{i}$ और आउटपुट वोल्टेज, $V_{0}$। इसलिए, उपरोक्त समीकरण से हमें क्षीणन कारक मिलेगा,$\alpha$ जैसा
$$\alpha = \frac{V_{i}}{V_{0}}=\frac{R_{1}+R_{2}}{R_{2}}$$
$\Rightarrow \alpha = 1+\frac{R_{1}}{R_{2}}$
$\Rightarrow \alpha-1 = \frac{R_{1}}{R_{2}}$
$\Rightarrow R_{1}= \left ( \alpha-1 \right )R_{2}$समीकरण २
समीकरण 2 से, हम यह निष्कर्ष निकाल सकते हैं कि का मान $R_{1}$ के पूर्णांक मानों के लिए than ?? '... 2 के मान से अधिक या बराबर है$\:\alpha > 1$।
समीकरण 1 में स्थानापन्न समीकरण 2।
$$\left ( \alpha-1 \right )R_{2}C_{1}=R_{2}C_{2}$$
$\Rightarrow \left ( \alpha-1 \right )C_{1} =C_{2}$
$\Rightarrow C_{1}=\frac{C_{2}}{\left ( \alpha-1 \right )}$समीकरण ३
समीकरण 3 से, हम यह निष्कर्ष निकाल सकते हैं कि का मान $C_{1}$ के मान के बराबर या उससे कम है $C_{2}$ के पूर्णांक मूल्यों के लिए $\alpha >1$
Example
आइए हम इसका मान ज्ञात करें $R_{1}$ तथा $C_{1}$ एक क्षीणन कारक होने की जांच,$\alpha$ 10. के रूप में मान लें, $R_{2}=1 M \Omega$ तथा $C_{2}=18pF$।
Step1 - हमें इसका मूल्य मिलेगा $R_{1}$ के मूल्यों को प्रतिस्थापित करके $\alpha$ तथा $R_{2}$ समीकरण 2 में।
$$ R_{1}=\left ( 10-1 \right )\times 1 \times 10^{6}$$
$$\Rightarrow R_{1}=9 \times 10^{6}$$
$$\Rightarrow R_{1}=9 M\Omega$$
Step 2 - हमें इसका मूल्य मिलेगा $C_{1}$ के मूल्यों को प्रतिस्थापित करके $\alpha$ तथा $C_{2}$ समीकरण 3 में।
$$C_{1}=\frac{18\times10^{-12}}{\left ( 10-1 \right )}$$
$$\Rightarrow C_{1}=2 \times 10^{-12}$$
$$\Rightarrow C_{1}=2 pF$$
इसलिए, के मूल्यों $R_{1}$ तथा $C_{1}$ एक जांच होगी $9M\Omega$ तथा $2pF$ क्रमशः दिए गए विनिर्देशों के लिए।
सक्रिय जांच
यदि जांच प्रमुख में सक्रिय इलेक्ट्रॉनिक घटक होते हैं, तो इसे कहा जाता है active probe। सक्रिय जांच का ब्लॉक आरेख नीचे दिए गए आंकड़े में दिखाया गया है।

जैसा कि चित्र में दिखाया गया है, जांच प्रमुख में BJT एमिटर अनुयायी के साथ कैस्केड में एक FET स्रोत अनुयायी होता है। FET स्रोत अनुयायी उच्च इनपुट प्रतिबाधा और कम आउटपुट प्रतिबाधा प्रदान करता है। जबकि, BJT एमिटर फॉलोअर का उद्देश्य यह है कि यह बिगड़े हुए बेमेल को टालता है या समाप्त करता है।
सह-अक्षीय केबल और समाप्ति सर्किट जैसे अन्य दो भाग सक्रिय और निष्क्रिय दोनों जांच में समान रहते हैं।
यदि विद्युत घटकों को एक पुल या रिंग संरचना के रूप में व्यवस्थित किया जाता है, तो उस विद्युत सर्किट को ए कहा जाता है bridge। सामान्य तौर पर, पुल चार भुजाओं या शाखाओं के समूह के साथ एक लूप बनाता है। प्रत्येक शाखा में एक या दो विद्युत घटक हो सकते हैं।
पुलों के प्रकार
हम वोल्टेज सिग्नल के आधार पर ब्रिज सर्किट या पुलों को निम्न दो श्रेणियों में वर्गीकृत कर सकते हैं जिनके साथ उन्हें संचालित किया जा सकता है।
- डीसी ब्रिज
- एसी पुल
अब, हम इन दो पुलों के बारे में संक्षेप में चर्चा करते हैं।
डीसी ब्रिज
यदि पुल सर्किट को केवल डीसी वोल्टेज सिग्नल के साथ संचालित किया जा सकता है, तो यह डीसी पुल सर्किट है या बस DC bridge। अज्ञात प्रतिरोध के मूल्य को मापने के लिए डीसी पुलों का उपयोग किया जाता है। circuit diagram डीसी पुल जैसा दिखता है नीचे दिए गए आंकड़े में दिखाया गया है।
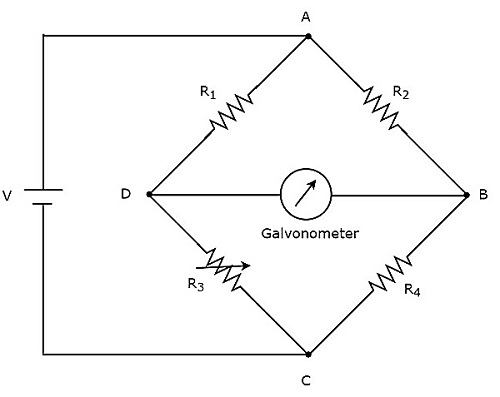
ऊपर डीसी पुल है four armsऔर प्रत्येक हाथ में एक रोकनेवाला होता है। जिसके बीच में, दो प्रतिरोधों का प्रतिरोध मान होता है, एक प्रतिरोधक एक चर अवरोधक होता है और दूसरे में अज्ञात प्रतिरोध मान होता है।
उपरोक्त डीसी ब्रिज सर्किट ए से उत्साहित हो सकता है DC voltage sourceएक विकर्ण में रखकर। गैल्वेनोमीटर को डीसी ब्रिज के अन्य विकर्ण में रखा गया है। यह कुछ विक्षेप दिखाता है जब तक कि पुल असंतुलित है।
परिवर्तनशील प्रतिरोध के भिन्न होने तक गैरीनोमीटर शून्य (शून्य) विक्षेप दिखाता है। अब, उपरोक्त डीसी पुल को संतुलित कहा जाता है। तो, हम इसका मूल्य पा सकते हैंunknown resistance नोडल समीकरणों का उपयोग करके।
एसी पुल
यदि ब्रिज सर्किट को केवल एसी वोल्टेज सिग्नल से संचालित किया जा सकता है, तो इसे एसी ब्रिज सर्किट या बस कहा जाता है AC bridge। एसी पुल का उपयोग अज्ञात अधिष्ठापन, समाई और आवृत्ति के मूल्य को मापने के लिए किया जाता है।
circuit diagram एसी पुल जैसा दिखता है नीचे दिए गए आंकड़े में दिखाया गया है।

एसी ब्रिज का सर्किट आरेख डीसी ब्रिज के समान है। उपरोक्त एसी पुल हैfour armsऔर प्रत्येक हाथ में कुछ प्रतिबाधा होती है। इसका मतलब है, प्रत्येक हाथ या तो एकल या निष्क्रिय तत्वों का संयोजन होगा जैसे कि अवरोधक, प्रारंभ करनेवाला और संधारित्र।
चार प्रतिबाधाओं के बीच, दो प्रतिबाधाओं के निश्चित मूल्य हैं, एक प्रतिबाधा परिवर्तनशील है और दूसरी एक अज्ञात प्रतिबाधा है।
उपरोक्त एसी ब्रिज सर्किट ए से उत्साहित हो सकता है AC voltage sourceएक विकर्ण में रखकर। एक डिटेक्टर को एसी ब्रिज के अन्य विकर्ण में रखा गया है। यह कुछ विक्षेप दिखाता है जब तक कि पुल असंतुलित है।
उपरोक्त एसी ब्रिज सर्किट ए से उत्साहित हो सकता है AC voltage sourceएक विकर्ण में रखकर। एक डिटेक्टर को एसी ब्रिज के अन्य विकर्ण में रखा गया है। यह कुछ विक्षेप दिखाता है जब तक कि पुल असंतुलित है।
चर प्रतिबाधा के प्रतिबाधा मान को तब तक भिन्न करें जब तक कि डिटेक्टर शून्य (शून्य) विक्षेपण नहीं दिखाता है। अब, उपरोक्त एसी पुल को संतुलित कहा जाता है। तो, हम इसका मूल्य पा सकते हैंunknown impedance संतुलित स्थिति का उपयोग करके।
DC bridgesकेवल डीसी वोल्टेज संकेत के साथ संचालित किया जा सकता है। डीसी ब्रिज अज्ञात प्रतिरोध के मूल्य को मापने के लिए उपयोगी हैं, जो पुल में मौजूद है। व्हीटस्टोन का पुल डीसी ब्रिज का एक उदाहरण है।
अब, हम के बारे में चर्चा करते हैं Wheatstone’s Bridge अज्ञात प्रतिरोध का मान ज्ञात करने के लिए।
व्हीटस्टोन का पुल
व्हीटस्टोन का पुल एक साधारण डीसी पुल है, जिसमें मुख्य रूप से चार हथियार होते हैं। इन चार भुजाओं में एक समचतुर्भुज या चौकोर आकार बनता है और प्रत्येक भुजा में एक रोकनेवाला होता है।
अज्ञात प्रतिरोध के मूल्य को खोजने के लिए, हमें गैल्वेनोमीटर और डीसी वोल्टेज स्रोत की आवश्यकता होती है। इसलिए, इन दोनों में से एक को व्हीटस्टोन के पुल के एक विकर्ण में रखा गया है और दूसरे को व्हीटस्टोन के पुल के दूसरे विकर्ण में रखा गया है।
मध्यम प्रतिरोध के मूल्य को मापने के लिए व्हीटस्टोन के पुल का उपयोग किया जाता है। circuit diagram व्हीटस्टोन के पुल को नीचे की आकृति में दिखाया गया है।
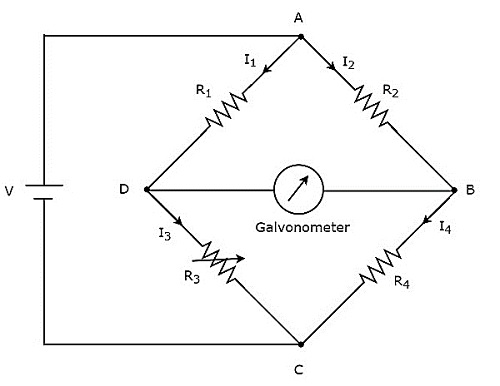
उपरोक्त सर्किट में, हथियार AB, BC, CD और DA एक साथ बनते हैं rhombusया चौकोर आकार। इनमें प्रतिरोधक होते हैं$R_{2}$, $R_{4}$, $R_{3}$ तथा $R_{1}$क्रमशः। बता दें कि इन रेसिस्टर आर्म्स के जरिए करंट प्रवाहित होता है$I_{2}$, $I_{4}$, $I_{3}$ तथा $I_{1}$ इन धाराओं के क्रमशः और दिशाओं को चित्र में दिखाया गया है।
विकर्ण हथियार डीबी और एसी क्रमशः गैल्वेनोमीटर और वी वोल्ट के डीसी वोल्टेज स्रोत के होते हैं। यहाँ, रोकनेवाला,$R_{3}$ एक मानक चर रोकनेवाला और रोकनेवाला है, $R_{4}$अज्ञात अवरोधक है। हम कर सकते हैंbalance the bridge, रोकनेवाला के प्रतिरोध मान को अलग करके, $R_{3}$।
उपरोक्त पुल सर्किट तब संतुलित होता है जब कोई भी धारा विकर्ण भुजा, DB से प्रवाहित नहीं होती है। इसका मतलब है, वहाँ हैno deflection गैल्वेनोमीटर में, जब पुल संतुलित होता है।
पुल संतुलित होगा, जब निम्नलिखित two conditions संतुष्ट हैं।
भुजा AD के पार वोल्टेज भुजा AB के पार वोल्टेज के बराबर है। अर्थात,
$$V_{AD}=V_{AB}$$
$\Rightarrow I_{1}R_{1}=I_{2}R_{2}$समीकरण 1
आर्म डीसी के पार वोल्टेज आर्म बीसी भर के वोल्टेज के बराबर होता है। अर्थात,
$$V_{DC}=V_{BC}$$
$\Rightarrow I_{3}R_{3}=I_{4}R_{4}$समीकरण २
ऊपर से दो संतुलन की स्थिति में, हम निम्नलिखित प्राप्त करेंगे two conclusions.
भुजा AD के माध्यम से बहने वाली धारा भुजा DC के बराबर होगी। अर्थात,
$$I_{1}=I_{3}$$
हाथ एबी के माध्यम से बहने वाली धारा हाथ ईसा पूर्व के बराबर होगी। अर्थात,
$$I_{2}=I_{4}$$
समीकरण 1 और समीकरण 2 का अनुपात लें।
$\frac{I_{1}R_{1}}{I_{3}R_{3}}=\frac{I_{2}R_{2}}{I_{4}R_{4}}$समीकरण ३
विकल्प, $I_{1}=I_{3}$ तथा $I_{2}=I_{4}$ समीकरण 3 में।
$$\frac{I_{3}R_{1}}{I_{3}R_{3}}=\frac{I_{4}R_{2}}{I_{4}R_{4}}$$
$$\Rightarrow \frac{R_{1}}{R_{3}}=\frac{R_{2}}{R_{4}}$$
$$\Rightarrow R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$
प्रतिरोधों के ज्ञात मूल्यों को प्रतिस्थापित करके $R_{1}$, $R_{2}$ तथा $R_{3}$ उपरोक्त समीकरण में, हम प्राप्त करेंगे value of resistor,$R_{4}$।
इस अध्याय में, एसी पुलों के बारे में चर्चा करते हैं, जिनका उपयोग अधिष्ठापन को मापने के लिए किया जा सकता है। एसी ब्रिज केवल एसी वोल्टेज सिग्नल के साथ काम करते हैं। circuit diagram एसी ब्रिज को नीचे दिए गए आंकड़े में दिखाया गया है।
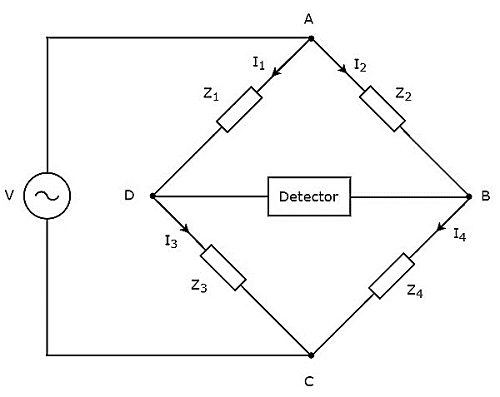
जैसा कि ऊपर की आकृति में दिखाया गया है, एसी ब्रिज में मुख्य रूप से चार भुजाएँ होती हैं, जो कि रोम्बस में जुड़ी होती हैं या square shape। इन सभी हथियारों में कुछ प्रतिबाधा होती है।
अज्ञात प्रतिबाधा के मूल्य का पता लगाने के लिए डिटेक्टर और एसी वोल्टेज स्रोत की भी आवश्यकता होती है। इसलिए, इन दोनों में से एक को एसी ब्रिज के एक विकर्ण में रखा गया है और दूसरे को एसी पुल के अन्य विकर्ण में रखा गया है। व्हीटस्टोन के पुल की संतुलन की स्थिति -
$$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$
हमें मिलेगा balancing condition of AC bridge, बस उपरोक्त समीकरण में Z के साथ R को प्रतिस्थापित करके।
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$\Rightarrow Z_{1}Z_{4}=Z_{2}Z_{3}$
यहाँ, $Z_{1}$ तथा $Z_{2}$निश्चित बाधाएं हैं। जहाँ तक,$Z_{3}$ एक मानक चर प्रतिबाधा है और $Z_{4}$ एक अज्ञात बाधा है।
Note - हम उन चार प्रतिबाधाओं में से किसी दो को नियत प्रतिबाधा के रूप में चुन सकते हैं, एक प्रतिबाधा मानक चर प्रतिबाधा के रूप में और दूसरी प्रतिबाधा एक अज्ञात प्रतिबाधा के रूप में अनुप्रयोग के आधार पर।
निम्नलिखित दो एसी पुल हैं, जिनका उपयोग मापने के लिए किया जा सकता है inductance।
- मैक्सवेल का पुल
- हाय का पुल
अब, हम एक-एक करके इन दो एसी पुलों के बारे में चर्चा करते हैं।
मैक्सवेल का पुल
मैक्सवेल का पुल एक एसी पुल है, जिसमें चार भुजाएँ हैं, जो एक नाभि के रूप में जुड़ी हुई हैं square shape। इस पुल की दो भुजाओं में एक एकल रोकनेवाला होता है, एक हाथ में रोकनेवाला और प्रारंभ करनेवाला की श्रृंखला संयोजन होता है और दूसरे हाथ में रोकनेवाला और संधारित्र के समानांतर संयोजन होता है।
अज्ञात प्रतिबाधा का मान ज्ञात करने के लिए एक एसी डिटेक्टर और एसी वोल्टेज स्रोत का उपयोग किया जाता है। इसलिए, इन दोनों में से एक को मैक्सवेल के पुल के एक विकर्ण में रखा गया है और दूसरे को मैक्सवेल के पुल के अन्य विकर्ण में रखा गया है।
मैक्सवेल के पुल का उपयोग मध्यम अधिष्ठापन के मूल्य को मापने के लिए किया जाता है। circuit diagram मैक्सवेल के पुल को नीचे दिए गए आंकड़े में दिखाया गया है।
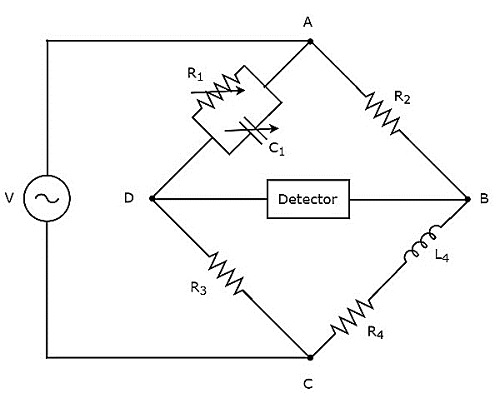
उपरोक्त सर्किट में, हथियार एबी, बीसी, सीडी और डीए एक साथ एक रंबल या चौकोर आकार बनाते हैं। हथियार एबी और सीडी में प्रतिरोधक होते हैं,$R_{2}$ तथा $R_{3}$क्रमशः। भुजा, BC में रोकनेवाला की एक श्रृंखला संयोजन होता है,$R_{4}$ और प्रारंभ करनेवाला, $L_{4}$। भुजा, DA में रोकनेवाला का समानांतर संयोजन होता है,$R_{1}$ और संधारित्र, $C_{1}$।
चलो, $Z_{1}, Z_{2}, Z_{3}$ तथा $Z_{4}$क्रमशः हथियार डीए, एबी, सीडी और बीसी की बाधाएं हैं। values of these impedances होगा
$$Z_{1}=\frac{R_{1}\left ( \frac{1}{j\omega C_{1}} \right )}{R_{1}+\frac{1}{j\omega C_{1}}}$$
$$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$$
$Z_{2}=R_{2}$
$Z_{3}=R_{3}$
$Z_{4}=R_{4}+j \omega L_{4}$
Substitute एसी पुल के निम्नलिखित संतुलन की स्थिति में ये प्रतिबाधा मूल्य।
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$$R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{\left ( {\frac{R_{1}}{1+j \omega R_{1}C_{1}}} \right )}$$
$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}\left (1+j \omega R_{1}C_{1} \right )}{R_{1}}$
$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+\frac{j \omega R_{1}C_{1}R_{2}R_{3}}{R_{1}}$
$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+j \omega C_{1}R_{2}R_{3}$
द्वारा comparing उपरोक्त समीकरण के संबंधित वास्तविक और काल्पनिक शब्द, हम प्राप्त करेंगे
$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$समीकरण 1
$L_{4}=C_{1}R_{2}R_{3}$समीकरण २
प्रतिरोधों के मूल्यों को प्रतिस्थापित करके $R_{1}$, $R_{2}$ तथा $R_{3}$ समीकरण 1 में, हमें रोकनेवाला का मान मिलेगा, $R_{4}$। इसी प्रकार, संधारित्र के मान को प्रतिस्थापित करके,$C_{1}$ और प्रतिरोधों के मूल्य, $R_{2}$ तथा $R_{3}$ समीकरण 2 में, हमें प्रारंभकर्ता का मान मिलेगा, $L_{4}$।
advantage मैक्सवेल का पुल यह है कि दोनों प्रतिरोधक के मान, $R_{4}$ और एक प्रारंभ करनेवाला, $L_{4}$ आवृत्ति के मूल्य से स्वतंत्र हैं।
हाय का पुल
हेय का पुल मैक्सवेल के पुल का एक संशोधित संस्करण है, जिसे हम हाथ को संशोधित करके प्राप्त करते हैं, जिसमें प्रतिरोध और संधारित्र के समानांतर संयोजन को हाथ में रखा जाता है, जिसमें मैक्सवेल के पुल में प्रतिरोधक और संधारित्र का एक श्रृंखला संयोजन होता है।
हाय के पुल का उपयोग उच्च अधिष्ठापन के मूल्य को मापने के लिए किया जाता है। circuit diagram हाय के पुल को नीचे दिए गए आंकड़े में दिखाया गया है।
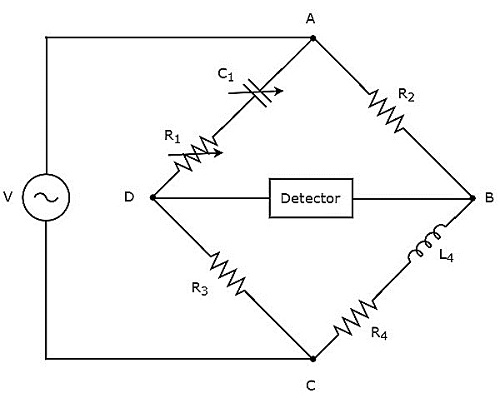
उपरोक्त सर्किट में, हथियार एबी, बीसी, सीडी और डीए एक साथ एक रंबल या चौकोर आकार बनाते हैं। हथियार, एबी और सीडी में प्रतिरोधक होते हैं,$R_{2}$ तथा $R_{3}$क्रमशः। भुजा, BC में रोकनेवाला की एक श्रृंखला संयोजन होता है,$R_{4}$ और प्रारंभ करनेवाला, $L_{4}$। भुजा, DA में रोकनेवाला की एक श्रृंखला संयोजन होता है,$R_{1}$ और संधारित्र, $C_{1}$।
चलो, $Z_{1}, Z_{2}, Z_{3}$ तथा $Z_{4}$क्रमशः हथियार डीए, एबी, सीडी और बीसी की बाधाएं हैं। values of these impedances होगा
$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$
$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$
$Z_{2}=R_{2}$
$Z_{3}=R_{3}$
$Z_{4}=R_{4}+j \omega L_{4}$
Substitute एसी पुल के निम्नलिखित संतुलन की स्थिति में ये प्रतिबाधा मूल्य।
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}}{\left ( \frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}\right )}$
$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1}\right )}$
इसके साथ समीकरण के दाहिने हाथ की अवधि के अंश और हर को गुणा करें $1 - j \omega R_{1}C_{1}$।
$\Rightarrow R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1}\right )}\times \frac{\left (1 - j \omega R_{1}C_{1} \right )}{\left (1 - j \omega R_{1}C_{1} \right )}$
$\Rightarrow R_{4}+j \omega L_{4}=\frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}+j \omega R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$
द्वारा comparing उपरोक्त समीकरण के संबंधित वास्तविक और काल्पनिक शब्द, हम प्राप्त करेंगे
$R_{4}= \frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$समीकरण ३
$L_{4}= \frac{R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$समीकरण ४
के मूल्यों को प्रतिस्थापित करके $R_{1}, R_{2}, R_{3}, C_{1}$ तथा $\omega$ समीकरण 3 और समीकरण 4 में, हमें रोकनेवाला का मान मिलेगा, $R_{4}$ और प्रारंभ करनेवाला, $L_{4}$।
पिछले अध्याय में, हमने दो एसी पुलों के बारे में चर्चा की, जिनका उपयोग अधिष्ठापन को मापने के लिए किया जा सकता है। इस अध्याय में, हम निम्नलिखित के बारे में चर्चा करते हैंtwo AC bridges।
- Schering Bridge
- वीनस ब्रिज
इन दो पुलों का उपयोग क्रमशः समाई और आवृत्ति को मापने के लिए किया जा सकता है।
Schering Bridge
श्रिंग ब्रिज एक एसी ब्रिज होता है, जिसमें चार भुजाएँ होती हैं, जो एक रोम्बस या के रूप में जुड़ी होती हैं square shape, जिसके एक हाथ में एक एकल रोकनेवाला होता है, एक हाथ में रोकनेवाला और संधारित्र की एक श्रृंखला संयोजन होता है, एक हाथ में एक संधारित्र होता है और दूसरे हाथ में रोकनेवाला और संधारित्र के समानांतर संयोजन होता है।
एसी डिटेक्टर और एसी वोल्टेज स्रोत का उपयोग अज्ञात प्रतिबाधा के मूल्य का पता लगाने के लिए भी किया जाता है, इसलिए उनमें से एक को Schering ब्रिज के एक विकर्ण में रखा गया है और दूसरे को Schering ब्रिज के अन्य विकर्ण में रखा गया है।
कैपिंग ब्रिज का उपयोग कैपेसिटेंस के मान को मापने के लिए किया जाता है। circuit diagram Schering ब्रिज का चित्र नीचे दिया गया है।
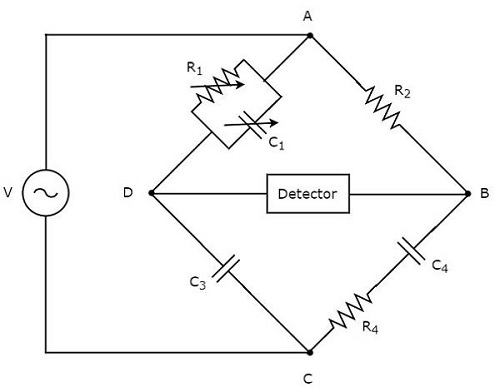
उपरोक्त सर्किट में, हथियार एबी, बीसी, सीडी और डीए एक साथ एक रोम्बस या बनाते हैं square shape। भुजा AB में एक प्रतिरोधक होता है,$R_{2}$। भुजा BC में रोकनेवाला की एक श्रृंखला संयोजन होता है,$R_{4}$ और संधारित्र, $C_{4}$। हाथ की सीडी में एक संधारित्र होता है,$C_{3}$। हाथ डीए में रोकनेवाला का एक समानांतर संयोजन होता है,$R_{1}$ और संधारित्र, $C_{1}$।
चलो, $Z_{1}$, $Z_{2}$,$Z_{3}$ तथा $Z_{4}$क्रमशः हथियार डीए, एबी, सीडी और बीसी की बाधाएं हैं। values of these impedances होगा
$Z_{1}=\frac{R_{1}\left ( \frac{1}{j \omega C_{1}} \right )}{R_{1}+\frac{1}{j \omega C_{1}}}$
$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$
$Z_{2}=R_{2}$
$Z_{3}=\frac{1}{j \omega C_{3}}$
$Z_{4}=R_{4}+\frac{1}{j \omega C_{4}}$
$\Rightarrow Z_{4}=\frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}$
Substitute एसी पुल के निम्नलिखित संतुलन की स्थिति में ये प्रतिबाधा मूल्य।
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$$\frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}=\frac{R_{2}\left (\frac{1}{j \omega C_{3}} \right )}{\frac{R_{1}}{1+j \omega R_{1}C_{1}}}$$
$\Rightarrow \frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}=\frac{R_{2}\left ( 1+j \omega R_{1}C_{1} \right )}{j \omega R_{1}C_{3}}$
$\Rightarrow \frac{1+j \omega R_{4}C_{4}}{C_{4}}=\frac{R_{2}\left ( 1+j \omega R_{1}C_{1} \right )}{R_{1}C_{3}}$
$\Rightarrow \frac{1}{C_{4}}+j \omega R_{4}=\frac{R_{2}}{R_{1}C_{3}}+\frac{j\omega C_{1}R_{2}}{C_{3}}$
द्वारा comparing उपरोक्त समीकरण के संबंधित वास्तविक और काल्पनिक शब्द, हम प्राप्त करेंगे
$C_{4}=\frac{R_{1}C_{3}}{R_{2}}$समीकरण 1
$R_{4}=\frac{C_{1}R_{2}}{C_{3}}$समीकरण २
के मूल्यों को प्रतिस्थापित करके $R_{1}, R_{2}$ तथा $C_{3}$ समीकरण 1 में, हमें संधारित्र का मान मिलेगा, $C_{4}$। इसी तरह, के मूल्यों को प्रतिस्थापित करके$R_{2}, C_{1}$ तथा $C_{3}$ समीकरण 2 में, हमें रोकनेवाला का मान मिलेगा, $R_{4}$।
advantage शियरिंग ब्रिज का यह है कि दोनों प्रतिरोधक के मान, $R_{4}$ और संधारित्र, $C_{4}$ आवृत्ति के मूल्य से स्वतंत्र हैं।
वीनस ब्रिज
Wien’s bridgeएक एसी ब्रिज है जिसमें चार भुजाएँ होती हैं, जो एक रंबल या चौकोर आकार के रूप में जुड़ी होती हैं। बटुओं की भुजाओं में एक एकल रोकनेवाला होता है, एक हाथ में रोकनेवाला और संधारित्र के समानांतर संयोजन होता है और दूसरे हाथ में रोकनेवाला और संधारित्र का एक श्रृंखला संयोजन होता है।
आवृत्ति का मान ज्ञात करने के लिए एसी डिटेक्टर और एसी वोल्टेज स्रोत की भी आवश्यकता होती है। इसलिए, इन दोनों में से एक को वेन के पुल के एक विकर्ण में रखा गया है और दूसरे को दूसरे को वेन के पुल के अन्य विकर्ण में रखा गया है।
circuit diagram नीचे विवरण में दिखाया गया है।
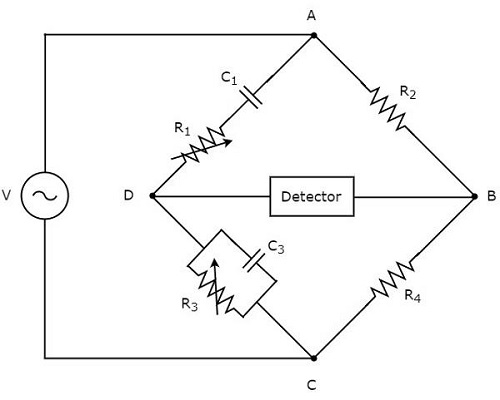
उपरोक्त सर्किट में, हथियार एबी, बीसी, सीडी और डीए एक साथ एक रोम्बस या बनाते हैं square shape। हथियार, AB और BC प्रतिरोधों से मिलकर बने होते हैं,$R_{2}$ तथा $R_{4}$क्रमशः। हाथ, सीडी में रोकनेवाला के समानांतर संयोजन होता है,$R_{3}$ और संधारित्र, $C_{3}$। भुजा, DA में रोकनेवाला की एक श्रृंखला संयोजन होता है,$R_{1}$ और संधारित्र, $C_{1}$।
चलो, $Z_{1}, Z_{2}, Z_{3}$ तथा $Z_{4}$क्रमशः हथियार डीए, एबी, सीडी और बीसी की बाधाएं हैं। values of these impedances होगा
$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$
$$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$$
$Z_{2}=R_{2}$
$$Z_{3}=\frac{R_{3}\left (\frac{1}{j \omega C_{3}} \right )}{R_{3}+\frac{1}{j \omega C_{3}}}$$
$$\Rightarrow Z_{3}= \frac{R_{3}}{1+j \omega R_{3}C_{3}}$$
$Z_{4}=R_{4}$
Substitute एसी पुल के निम्नलिखित संतुलन की स्थिति में ये प्रतिबाधा मूल्य।
$$Z_{1}Z_{4}=Z_{2}Z_{3}$$
$$\left (\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}} \right )R_{4}=R_{2}\left (\frac{R_{3}}{1+j \omega R_{3}C_{3}} \right )$$
$\Rightarrow \left (1+j \omega R_{1}C_{1}\right )\left (1+j \omega R_{3}C_{3}\right )R_{4}=j \omega C_{1}R_{2}R_{3}$
$\Rightarrow \left (1+j \omega R_{3}C_{3}+j \omega R_{1}C_{1}-\omega^{2}R_{1}R_{3}C_{1}C_{3}\right )R_{4}=j \omega C_{1}R_{2}R_{3}$
$\Rightarrow R_{4}\left ( \omega^{2}R_{1}R_{3}C_{1}C_{3} \right )+j \omega R_{4}\left (R_{3}C_{3}+R_{1}C_{1} \right )=j \omega C_{1}R_{2}R_{3}$
Equate अपने अपने real terms समीकरण के ऊपर।
$$R_{4}\left (1- \omega^{2}R_{1}R_{3}C_{1}C_{3} \right )=0$$
$\Rightarrow 1- \omega^{2}R_{1}R_{3}C_{1}C_{3} =0$
$\Rightarrow 1= \omega^{2}R_{1}R_{3}C_{1}C_{3}$
$\omega = \frac{1}{\sqrt{R_{1}R_{3}C_{1}C_{3}}}$
Substitute, $\omega = 2 \pi f$ उपरोक्त समीकरण में।
$$\Rightarrow 2 \pi f= \frac{1}{\sqrt{R_{1}R_{3}C_{1}C_{3}}}$$
$\Rightarrow f= \frac{1}{2 \pi\sqrt{R_{1}R_{3}C_{1}C_{3}}}$
हम आवृत्ति का मान पा सकते हैं, $f$ के मूल्यों को प्रतिस्थापित करके एसी वोल्टेज स्रोत $R_{1}, R_{3}, C_{1}$ तथा $C_{3}$ उपरोक्त समीकरण में।
अगर $R_{1}=R_{3}=R$ तथा $C_{1}=C_{3}=C$, तो हम आवृत्ति का मान पा सकते हैं, $f$ निम्नलिखित सूत्र का उपयोग करके एसी वोल्टेज स्रोत।
$$f=\frac{1}{2\pi RC}$$
वेइन का पुल मुख्य रूप से खोजने के लिए उपयोग किया जाता है frequency value वायुसेना रेंज की।
मूल रूप से, ट्रांसड्यूसर ऊर्जा के एक रूप को ऊर्जा के दूसरे रूप में परिवर्तित करता है। ट्रांसड्यूसर, जो ऊर्जा के गैर-विद्युत रूप को विद्युत के रूप में परिवर्तित करता है, ऊर्जा के रूप में जाना जाता हैelectrical transducer। block diagram विद्युत ट्रांसड्यूसर के नीचे चित्र में दिखाया गया है।
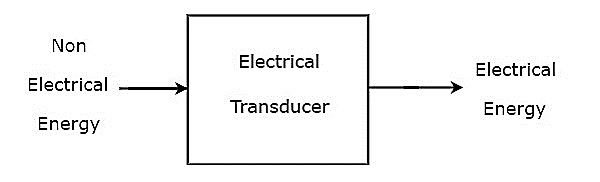
जैसा कि चित्र में दिखाया गया है, विद्युत ट्रांसड्यूसर एक आउटपुट का उत्पादन करेगा, जिसमें विद्युत ऊर्जा है। विद्युत ट्रांसड्यूसर का आउटपुट इनपुट के बराबर है, जिसमें गैर-विद्युत ऊर्जा है।
विद्युत ट्रांसड्यूसर के प्रकार
मुख्य रूप से, विद्युत ट्रांसड्यूसर को निम्नलिखित में वर्गीकृत किया जा सकता है two types।
- सक्रिय ट्रांसड्यूसर
- निष्क्रिय ट्रांसड्यूसर
अब, हम इन दो प्रकार के ट्रांसड्यूसर के बारे में संक्षेप में चर्चा करते हैं।
सक्रिय ट्रांसड्यूसर
ट्रांसड्यूसर, जो विद्युत मात्रा में से एक का उत्पादन कर सकता है जैसे कि वोल्टेज और वर्तमान के रूप में जाना जाता है active transducer। इसे स्व-उत्पादक ट्रांसड्यूसर भी कहा जाता है, क्योंकि इसके लिए किसी बाहरी बिजली की आपूर्ति की आवश्यकता नहीं होती है।
block diagram सक्रिय ट्रांसड्यूसर के नीचे चित्र में दिखाया गया है।
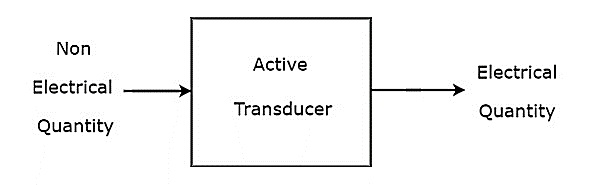
जैसा कि चित्र में दिखाया गया है, सक्रिय ट्रांसड्यूसर एक विद्युत मात्रा (या संकेत) का उत्पादन करेगा, जो गैर-विद्युत इनपुट मात्रा (या संकेत) के बराबर है।
Examples
सक्रिय ट्रांसड्यूसर के उदाहरण निम्नलिखित हैं।
- पीजो इलेक्ट्रिक ट्रांसड्यूसर
- फोटो इलेक्ट्रिक ट्रांसड्यूसर
- थर्मो इलेक्ट्रिक ट्रांसड्यूसर
हम अगले अध्याय में इन सक्रिय ट्रांसड्यूसर के बारे में चर्चा करेंगे।
निष्क्रिय ट्रांसड्यूसर
ट्रांसड्यूसर, जो विद्युत मात्रा का उत्पादन नहीं कर सकता जैसे कि वोल्टेज और करंट के रूप में जाना जाता है passive transducer। लेकिन, यह प्रतिरोधक (आर), प्रारंभ करनेवाला (एल) और कैपेसिटर (सी) जैसे निष्क्रिय तत्वों में से एक में भिन्नता पैदा करता है। निष्क्रिय ट्रांसड्यूसर को बाहरी बिजली की आपूर्ति की आवश्यकता होती है।
block diagram निष्क्रिय ट्रांसड्यूसर के नीचे चित्र में दिखाया गया है।
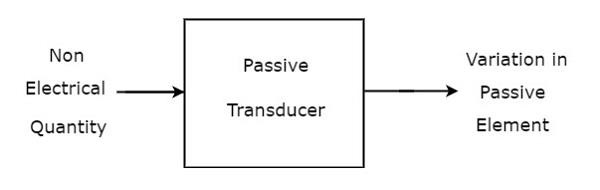
जैसा कि चित्र में दिखाया गया है, निष्क्रिय ट्रांसड्यूसर गैर-विद्युत इनपुट मात्रा (या संकेत) में भिन्नता के अनुसार निष्क्रिय तत्व में भिन्नता पैदा करेगा।
Examples
निम्नलिखित निष्क्रिय ट्रांसड्यूसर्स के उदाहरण हैं।
- प्रतिरोधक ट्रांसड्यूसर
- प्रेरक ट्रांसड्यूसर
- कैपेसिटिव ट्रांसड्यूसर
हम बाद के अध्यायों में इन निष्क्रिय ट्रांसड्यूसर के बारे में चर्चा करेंगे।
Active transducerएक ट्रांसड्यूसर है, जो गैर-विद्युत मात्रा को विद्युत मात्रा में परिवर्तित करता है। आइए हम गैर-विद्युत मात्रा जैसे दबाव, प्रकाश और तापमान की रोशनी पर विचार करें। इसलिए, हमारे द्वारा चुने गए गैर-विद्युत मात्रा के आधार पर हमें निम्नलिखित तीन सक्रिय ट्रांसड्यूसर मिलेंगे।
- पीजो इलेक्ट्रिक ट्रांसड्यूसर
- फोटो इलेक्ट्रिक ट्रांसड्यूसर
- थर्मो इलेक्ट्रिक ट्रांसड्यूसर
अब, इन तीन सक्रिय ट्रांसड्यूसर के बारे में एक-एक करके चर्चा करते हैं।
पीजो इलेक्ट्रिक ट्रांसड्यूसर
एक सक्रिय ट्रांसड्यूसर कहा जाता है piezo electric transducer, जब यह एक विद्युत मात्रा का उत्पादन करता है जो दबाव इनपुट के बराबर होता है। निम्नलिखित तीन पदार्थ पीजो इलेक्ट्रिक प्रभाव प्रदर्शित करते हैं।
- Quartz
- रोशेल साल्ट
- Tourmaline
इन तीन पदार्थों द्वारा प्रदर्शित पीजो-विद्युत प्रभाव टूमलाइन, क्वार्ट्ज और रोशेल लवण है, इस आरोही क्रम में। इन तीन पदार्थों द्वारा होने वाली यांत्रिक शक्ति का आरोही क्रम रोशेल लवण, क्वार्ट्ज, टूमलाइन है।
Quartz इसे पीजो इलेक्ट्रिक ट्रांसड्यूसर के रूप में उपयोग किया जाता है, क्योंकि यह मध्यम पीजो इलेक्ट्रिक प्रभाव प्रदर्शित करता है और उन तीन पीजो इलेक्ट्रिक पदार्थों में मध्यम यांत्रिक शक्ति होती है।
क्वार्ट्ज ट्रांसड्यूसर
circuit diagramक्वार्ट्ज ट्रांसड्यूसर नीचे दिए गए आंकड़े में दिखाया गया है। जैसा कि चित्र में दिखाया गया है, क्वार्ट्ज क्रिस्टल को आधार और बल योग सदस्य के बीच रखा गया है। आउटपुट वोल्टेज को धातु इलेक्ट्रोड के पार मापा जा सकता है, जो क्वार्ट्ज क्रिस्टल के दो तरफ रखे जाते हैं।
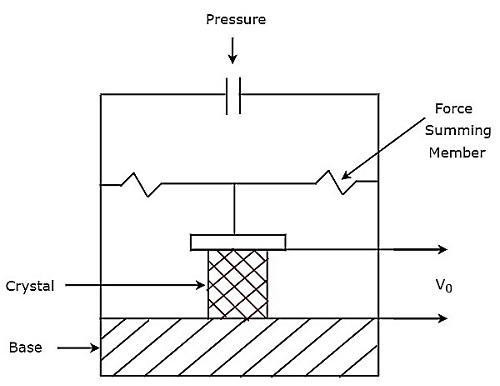
output voltage, $V_{0}$ के ऊपर दबाव ट्रांसड्यूसर होगा
$$V_{0}=\frac{Q}{C}$$
फोटो इलेक्ट्रिक ट्रांसड्यूसर
एक सक्रिय ट्रांसड्यूसर को फोटो इलेक्ट्रिक ट्रांसड्यूसर कहा जाता है, जब यह एक विद्युत मात्रा का उत्पादन करता है जो प्रकाश इनपुट की रोशनी के बराबर होता है। circuit diagram फोटो इलेक्ट्रिक ट्रांसड्यूसर नीचे दिए गए चित्र में दिखाया गया है।
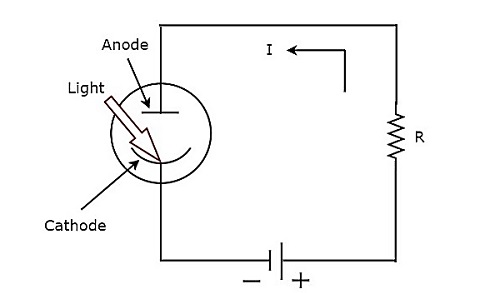
working फोटो इलेक्ट्रिक ट्रांसड्यूसर का उल्लेख नीचे किया गया है।
Step1 - फोटो विद्युत ट्रांसड्यूसर इलेक्ट्रॉनों को जारी करता है, जब प्रकाश इसके कैथोड पर गिरता है।
Step2 - फोटो इलेक्ट्रिक ट्रांसड्यूसर एक विद्युत धारा का उत्पादन करता है, मैं सर्किट में एनोड की ओर इलेक्ट्रॉनों के आकर्षण के कारण।
हम पा सकते हैं sensitivity निम्नलिखित सूत्र का उपयोग करके फोटो इलेक्ट्रिक ट्रांसड्यूसर की।
$$S=\frac{I}{i}$$
कहाँ पे,
$S$ फोटो इलेक्ट्रिक ट्रांसड्यूसर की संवेदनशीलता है
$I$ फोटो विद्युत ट्रांसड्यूसर का आउटपुट करंट है
$i$ फोटो विद्युत ट्रांसड्यूसर के प्रकाश इनपुट की रोशनी है
थर्मो इलेक्ट्रिक ट्रांसड्यूसर
एक सक्रिय ट्रांसड्यूसर कहा जाता है thermo electric transducer, जब यह एक विद्युत मात्रा का उत्पादन करता है जो तापमान इनपुट के बराबर होता है। निम्नलिखित दो ट्रांसड्यूसर थर्मो इलेक्ट्रिक ट्रांसड्यूसर के उदाहरण हैं।
- थर्मिस्टर ट्रांजिस्टर
- थर्मोकपल ट्रांसड्यूसर
अब, इन दो ट्रांसड्यूसर के बारे में एक-एक करके चर्चा करते हैं।
थर्मिस्टर ट्रांजिस्टर
रोकनेवाला, जो तापमान पर निर्भर करता है, थर्मल प्रतिरोधक कहलाता है। संक्षेप में, इसे कहा जाता हैThermistor। थर्मिस्टर का तापमान गुणांक नकारात्मक है। इसका मतलब है, जैसे-जैसे तापमान बढ़ता है, थर्मिस्टर का प्रतिरोध घटता जाता है।
Mathematicallyथर्मिस्टर और तापमान के प्रतिरोध के बीच संबंध के रूप में प्रतिनिधित्व किया जा सकता है
$$R_{1}=R_{2}e^\left ( \beta \left [ \frac{1}{T_{1}}-\frac{1}{T_{2}} \right ] \right )$$
Where,
$R_{1}$ तापमान पर थर्मिस्टर का प्रतिरोध है ${T_{1}}^{0}K$
$R_{2}$ तापमान पर थर्मिस्टर का प्रतिरोध है ${T_{2}}^{0}K$
$\beta$ तापमान स्थिर है
advantage थर्मिस्टर ट्रांजिस्टर यह है कि यह एक तेज़ और स्थिर प्रतिक्रिया देगा।
थर्मोकपल ट्रांसड्यूसर
थर्मोकपल ट्रांसड्यूसर इनपुट पर तापमान के इसी परिवर्तन के लिए एक आउटपुट वोल्टेज का उत्पादन करता है। यदि दो जंक्शन बनाने के लिए विभिन्न धातुओं के दो तारों को एक साथ जोड़ा जाता है, तो उस पूरे विन्यास को कहा जाता हैThermocouple। बुनियादी थर्मोकपल का सर्किट आरेख नीचे दिखाया गया है -
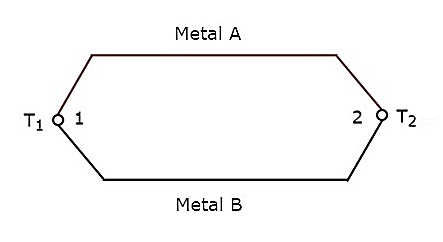
उपरोक्त थर्मोकपल में दो धातुएँ हैं, A & B और दो जंक्शन, 1 & 2. एक निरंतर संदर्भ तापमान पर विचार करें, $T_{2}$ जंक्शन पर 2. जंक्शन पर तापमान दें, 1 है $T_{1}$। थर्मोकपल एक उत्पन्न करता हैemf (इलेक्ट्रो मोटिव फोर्स), जब भी मूल्यों की $T_{1}$ तथा $T_{2}$ अलग है।
इसका मतलब है कि, थर्मोकपल एक ईएमएफ उत्पन्न करता है, जब भी दो जंक्शनों, 1 और 2 के बीच एक तापमान अंतर होता है और यह उन दो जंक्शनों के बीच तापमान के अंतर के सीधे आनुपातिक होता है। Mathematically, यह के रूप में प्रतिनिधित्व किया जा सकता है
$$e \alpha \left ( T_{1}-T_{2} \right )$$
कहाँ पे,
$e$ थर्मोपल द्वारा उत्पन्न ईएमएफ है
उपरोक्त थर्मोकपल सर्किट को व्यावहारिक अनुप्रयोगों के लिए नीचे दिए गए चित्र में दिखाया गया है।
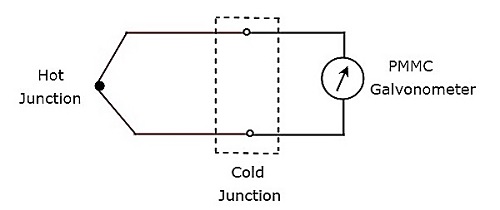
सर्किट का हिस्सा, जो उन दो जंक्शनों सहित गर्म और ठंडे जंक्शनों के बीच स्थित है, मूल थर्मोकपल का एक समान मॉडल है। एक PMMC गैल्वेनोमीटर ठंडे जंक्शन के पार जुड़ा हुआ है और यह ठंडे जंक्शन पर उत्पन्न ईएमएफ के अनुसार विक्षेपित होता है।Thermocouple transducer सबसे अधिक इस्तेमाल किया जाने वाला थर्मोइलेक्ट्रिक ट्रांसड्यूसर है।
passive transducerएक ट्रांसड्यूसर है, जो निष्क्रिय तत्व में भिन्नता पैदा करता है। हम प्रतिरोधक, प्रारंभ करनेवाला और संधारित्र जैसे निष्क्रिय तत्वों पर विचार करेंगे। इसलिए, हम निम्नलिखित तीन निष्क्रिय ट्रांसड्यूसर प्राप्त करेंगे जो हम चुनते हैं निष्क्रिय तत्व के आधार पर।
- प्रतिरोधक ट्रांसड्यूसर
- प्रेरक ट्रांसड्यूसर
- कैपेसिटिव ट्रांसड्यूसर
अब, हम इन तीन निष्क्रिय ट्रांसड्यूसर के बारे में एक-एक करके चर्चा करते हैं।
प्रतिरोधक ट्रांसड्यूसर
एक निष्क्रिय ट्रांसड्यूसर कहा जाता है एक resistive transducer, जब यह प्रतिरोध मूल्य में भिन्नता (परिवर्तन) पैदा करता है। निम्नलिखित सूत्रresistance, एक धातु कंडक्टर के।
$$R=\frac{\rho \:l}{A}$$
कहाँ पे,
$\rho$ कंडक्टर की प्रतिरोधकता है
$l$ कंडक्टर की लंबाई है
$A$ कंडक्टर का क्रॉस सेक्शनल क्षेत्र है
प्रतिरोध मान तीन मापदंडों पर निर्भर करता है $\rho, l$ और $A$। तो, हम कर सकते हैंresistive transducers तीन मापदंडों में से एक में भिन्नता के आधार पर $\rho, l$ और $A$। उन तीन मापदंडों में से किसी एक में भिन्नता प्रतिरोध मूल्य को बदल देती है।
प्रतिरोध, आर सीधे आनुपातिक है resistivity कंडक्टर का, $\rho$। तो, कंडक्टर की प्रतिरोधकता के रूप में,$\rho$प्रतिरोध के मूल्य को बढ़ाता है, आर भी बढ़ता है। इसी तरह, कंडक्टर की प्रतिरोधकता के रूप में,$\rho$ प्रतिरोध का मूल्य घटता है, R भी घटता है।
प्रतिरोध, आर सीधे आनुपातिक है length कंडक्टर का, $l$। तो, कंडक्टर की लंबाई के रूप में,$l$प्रतिरोध के मूल्य को बढ़ाता है, आर भी बढ़ता है। इसी तरह, कंडक्टर की लंबाई,$l$ प्रतिरोध का मूल्य घटता है, R भी घटता है।
प्रतिरोध, R व्युत्क्रम आनुपातिक है cross sectional area कंडक्टर के, $A$। तो, कंडक्टर के पार अनुभागीय क्षेत्र के रूप में,$A$प्रतिरोध का मान बढ़ाता है, R घटता है। इसी तरह, कंडक्टर के क्रॉस सेक्शनल क्षेत्र के रूप में,$A$ प्रतिरोध का मूल्य घटता है, R बढ़ता है।
प्रेरक ट्रांसड्यूसर
एक निष्क्रिय ट्रांसड्यूसर कहा जाता है एक inductive transducer, जब यह अधिष्ठापन मूल्य में भिन्नता (परिवर्तन) पैदा करता है। निम्नलिखित सूत्रinductance, प्रारंभ करनेवाला का।
$L=\frac{N^{2}}{S}$समीकरण 1
कहाँ पे,
$N$ कुंडल के घुमावों की संख्या है
$S$ कुंडल के घुमावों की संख्या है
निम्नलिखित सूत्र reluctance, कुंडल का।
$S=\frac{l}{\mu A}$समीकरण २
कहाँ पे,
$l$ चुंबकीय सर्किट की लंबाई है
$\mu$ कोर की पारगम्यता है
$A$ चुंबकीय सर्किट का वह क्षेत्र है जिसके माध्यम से प्रवाह प्रवाहित होता है
स्थानापन्न, समीकरण २ समीकरण १ में।
$$L=\frac{N^{2}}{\left (\frac{l}{\mu A} \right )}$$
$\Rightarrow L=\frac{N^{2}\mu A}{l}$समीकरण ३
समीकरण 1 और समीकरण 3 से, हम यह निष्कर्ष निकाल सकते हैं कि प्रेरण मान तीन मापदंडों पर निर्भर करता है $N,S$ और $\mu$। तो, हम कर सकते हैंinductive transducers तीन मापदंडों में से एक में भिन्नता के आधार पर $N,S$ और $\mu$। क्योंकि, उन तीन मापदंडों में से किसी एक में भिन्नता अधिष्ठापन मूल्य को बदल देती है।
इंडक्शन, एल सीधे वर्ग के आनुपातिक है number of turns of coil। तो, कुंडल के घुमावों की संख्या के रूप में,$N$ अधिष्ठापन के मूल्य को बढ़ाता है, $L$भी बढ़ता है। इसी तरह, कॉइल के घुमावों की संख्या के रूप में,$N$ अधिष्ठापन का मूल्य घटता है, $L$ भी घट जाती है।
उपपादन, $L$ के विपरीत आनुपातिक है reluctance of coil, $S$। तो, कुंडल की अनिच्छा के रूप में,$S$ अधिष्ठापन के मूल्य को बढ़ाता है, $L$घट जाती है। इसी तरह, कुंडल की अनिच्छा के रूप में,$S$ अधिष्ठापन का मूल्य घटता है, $L$ बढ़ती है।
अनिच्छा, एल सीधे आनुपातिक है permeability of core, $\mu$। तो, कोर की पारगम्यता के रूप में,$\mu$अधिष्ठापन के मूल्य को बढ़ाता है, एल भी बढ़ता है। इसी तरह, कोर की पारगम्यता के रूप में,$\mu$ अधिष्ठापन का मूल्य घटता है, L भी घटता है।
कैपेसिटिव ट्रांसड्यूसर
एक निष्क्रिय ट्रांसड्यूसर कहा जाता है एक capacitive transducer, जब यह समाई मूल्य में भिन्नता (परिवर्तन) पैदा करता है। निम्नलिखित सूत्रcapacitance, C एक समानांतर प्लेट संधारित्र।
$$C=\frac{\varepsilon A}{d}$$
कहाँ पे,
$\varepsilon$ क्रमबद्धता या ढांकता हुआ स्थिरांक है
$A$ दो प्लेटों का प्रभावी क्षेत्र है
$d$ दो प्लेटों का प्रभावी क्षेत्र है
समाई मान तीन मापदंडों पर निर्भर करता है $\varepsilon, A$ और $d$। तो, हम कर सकते हैंcapacitive transducers तीन मापदंडों में से एक में भिन्नता के आधार पर$\varepsilon, A$ और $d$। क्योंकि, उन तीन मापदंडों में से किसी एक में भिन्नता समाई मूल्य को बदल देती है।
समाई, सी सीधे आनुपातिक है permittivity, $\varepsilon$। तो, परमिट के रूप में,$\varepsilon$समाई का मूल्य बढ़ता है, सी भी बढ़ता है। इसी तरह, परमिट के रूप में,$\varepsilon$ समाई का मूल्य कम हो जाता है, C भी घट जाता है।
समाई, सी सीधे आनुपातिक है effective area of two plates, $A$। इसलिए, दो प्लेटों के प्रभावी क्षेत्र के रूप में,$A$समाई का मूल्य बढ़ता है, सी भी बढ़ता है। इसी तरह, दो प्लेटों के प्रभावी क्षेत्र के रूप में,$A$ समाई का मूल्य कम हो जाता है, C भी घट जाता है।
क्षमता, सी के विपरीत आनुपातिक है distance between two plates, $d$। तो, दो प्लेटों के बीच की दूरी के रूप में,$d$कैपेसिटेंस का मान बढ़ाता है, C घटता है। इसी तरह, दो प्लेटों के बीच की दूरी के रूप में,$d$ समाई का मूल्य घटता है, C बढ़ता है।
इस अध्याय में, हमने तीन निष्क्रिय ट्रांसड्यूसर के बारे में चर्चा की। अगले अध्याय में, हम प्रत्येक निष्क्रिय ट्रांसड्यूसर के लिए एक उदाहरण के बारे में चर्चा करते हैं।
physical quantitiesजैसे कि विस्थापन, वेग, बल, तापमान और आदि सभी गैर-विद्युत मात्राएँ हैं। सक्रिय ट्रांसड्यूसर भौतिक मात्रा को विद्युत संकेत में परिवर्तित करता है। जबकि, निष्क्रिय ट्रांसड्यूसर भौतिक मात्रा को निष्क्रिय तत्व में भिन्नता में परिवर्तित करता है।
तो, आवश्यकता के आधार पर हम सक्रिय ट्रांसड्यूसर या निष्क्रिय ट्रांसड्यूसर चुन सकते हैं। इस अध्याय में, आइए चर्चा करें कि एक निष्क्रिय ट्रांसड्यूसर का उपयोग करके विस्थापन को कैसे मापें। यदि एक शरीर जो एक बिंदु से दूसरे बिंदु तक सीधी रेखा में जाता है, तो उन दो बिंदुओं के बीच की लंबाई को कहा जाता हैdisplacement।
हमारे पास निम्नलिखित हैं three passive transducers
- प्रतिरोधक ट्रांसड्यूसर
- प्रेरक ट्रांसड्यूसर
- कैपेसिटिव ट्रांसड्यूसर
अब, आइए एक-एक करके इन तीन निष्क्रिय ट्रांसड्यूसर के साथ विस्थापन के माप के बारे में चर्चा करें।
प्रतिरोधक ट्रांसड्यूसर का उपयोग कर विस्थापन का मापन
circuit diagram प्रतिरोधक ट्रांसड्यूसर, जिसका उपयोग विस्थापन को मापने के लिए किया जाता है, नीचे दिए गए आंकड़े में दिखाया गया है।
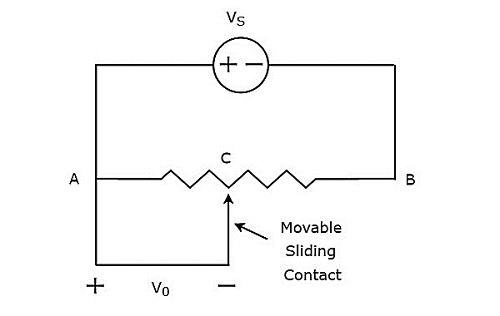
उपरोक्त सर्किट में एक पोटेंशियोमीटर और एक वोल्टेज स्रोत होता है, $V_{S}$। हम कह सकते हैं कि ये दोनों अंक ए और बी पोटेंशियोमीटर के संबंध में समानांतर रूप से जुड़े हुए हैं, इसमें एक स्लाइडिंग संपर्क है, जो विविध हो सकता है। तो, बिंदु C एक परिवर्तनशील है। उपरोक्त सर्किट में,output voltage, $V_{0}$ अंक ए और सी के पार मापा जाता है।
Mathematicallyवोल्टेज और दूरियों के बीच के संबंध को इस रूप में दर्शाया जा सकता है
$$\frac{V_{0}}{V_{S}}=\frac{AC}{AB}$$
इसलिए, हमें उस शरीर को कनेक्ट करना चाहिए जिसका विस्थापन स्लाइडिंग संपर्क से मापा जाना है। इसलिए, जब भी शरीर एक सीधी रेखा में चलता है, तो बिंदु C भी बदलता रहता है। इसके कारण, आउटपुट वोल्टेज,$V_{0}$ तदनुसार भी बदलता है।
इस मामले में, हम आउटपुट वोल्टेज को मापकर विस्थापन पा सकते हैं, $V_{0}$।
प्रेरणात्मक ट्रांसड्यूसर का उपयोग कर विस्थापन का मापन
circuit diagram आगमनात्मक ट्रांसड्यूसर, जिसका उपयोग विस्थापन को मापने के लिए किया जाता है, नीचे दिए गए आंकड़े में दिखाया गया है।
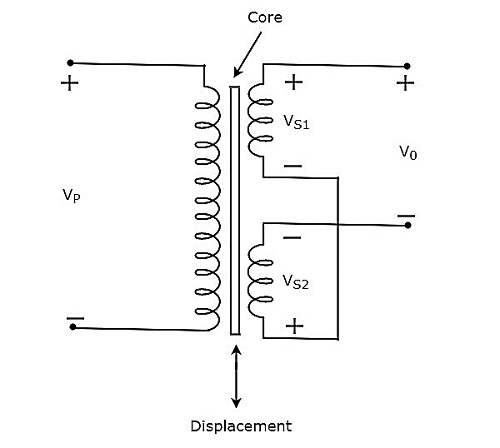
उपरोक्त सर्किट में मौजूद ट्रांसफार्मर में एक प्राथमिक वाइंडिंग और दो सेकेंडरी वाइंडिंग होते हैं। यहां, दो माध्यमिक वाइंडिंग के अंतिम बिंदु एक साथ जुड़ जाते हैं। तो, हम कह सकते हैं कि ये दो माध्यमिक घुमाव जुड़े हुए हैंseries opposition।
वोल्टेज, $V_{P}$ट्रांसफार्मर की प्राथमिक घुमावदार में लागू किया जाता है। बता दें, प्रत्येक माध्यमिक घुमावदार में विकसित वोल्टेज '??' ð † ?? '† 1 और ð ??' '' ?? '' 2 है। आउटपुट वोल्टेज,$V_{0}$ दो माध्यमिक वाइंडिंग के शुरुआती बिंदुओं पर लिया जाता है।
Mathematicallyआउटपुट वोल्टेज, '??' output 0 के रूप में लिखा जा सकता है
$$V_{0}= V_{S1}-V_{S2}$$
उपरोक्त सर्किट में मौजूद ट्रांसफार्मर को कहा जाता है differential transformer, क्योंकि यह एक आउटपुट वोल्टेज का उत्पादन करता है, जो कि अंतर है $V_{S1}$ तथा $V_{S2}$।
यदि कोर केंद्रीय स्थिति में है, तो आउटपुट वोल्टेज, $V_{0}$शून्य के बराबर होगा। क्योंकि, संबंधित परिमाण और चरण$V_{S1}$ तथा $V_{S2}$ समान हैं।
यदि कोर केंद्रीय स्थिति में नहीं है, तो आउटपुट वोल्टेज, $V_{0}$कुछ परिमाण और चरण होंगे। क्योंकि, संबंधित परिमाण और चरण$V_{S1}$ तथा $V_{S2}$ बराबर नहीं हैं।
इसलिए, हमें उस शरीर को जोड़ना चाहिए जिसका विस्थापन केंद्रीय कोर से मापा जाना है। इसलिए, जब भी शरीर एक सीधी रेखा में चलता है, कोर की केंद्रीय स्थिति बदलती है। इसके कारण, आउटपुट वोल्टेज,$V_{0}$ तदनुसार भी बदलता है।
इस मामले में, हम पा सकते हैं displacement आउटपुट वोल्टेज को मापने के द्वारा, $V_{0}$। उत्पादन वोल्टेज का परिमाण और चरण,$V_{0}$ क्रमशः शरीर के विस्थापन और उसकी दिशा का प्रतिनिधित्व करता है।
कैपेसिटिव ट्रांसड्यूसर का उपयोग कर विस्थापन का मापन
circuit diagram कैपेसिटिव ट्रांसड्यूसर, जिसका उपयोग विस्थापन को मापने के लिए किया जाता है, नीचे दिए गए आंकड़े में दिखाया गया है।
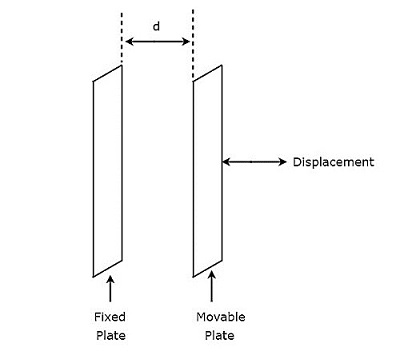
capacitor, जो उपरोक्त सर्किट में मौजूद है, दो समानांतर प्लेट हैं। जिसके बीच में एक प्लेट फिक्स है और दूसरी प्लेट एक चल है। इसके कारण, इन दोनों प्लेटों के बीच अंतर भी अलग-अलग होगा। कैपेसिटर परिवर्तन के दो प्लेटों के बीच रिक्ति के रूप में कैपेसिटेंस परिवर्तनों का मूल्य।
इसलिए, हमें उस शरीर से जुड़ना चाहिए, जिसका displacementएक संधारित्र के जंगम प्लेट के लिए मापा जाना है। इसलिए, जब भी शरीर एक सीधी रेखा में चलता है, तो संधारित्र की दो प्लेटों के बीच अंतर भिन्न होता है। इसके कारण, समाई मान बदल जाता है।
डेटा अधिग्रहण के लिए उपयोग किए जाने वाले सिस्टम को कहा जाता है data acquisition systems। ये डेटा अधिग्रहण प्रणालियां डेटा के रूपांतरण, डेटा के भंडारण, डेटा के संचरण और डेटा के प्रसंस्करण जैसे कार्यों का प्रदर्शन करेंगी।
डाटा अधिग्रहण प्रणाली निम्नलिखित पर विचार करती है analog signals।
एनालॉग सिग्नल, जो डीसी और एसी वोल्टेज, डीसी और एसी धाराओं, प्रतिरोध और आदि जैसे विद्युत मात्रा के प्रत्यक्ष माप से प्राप्त होते हैं।
एनालॉग सिग्नल, जो ट्रांसड्यूसर जैसे LVDT, थर्मोकपल और आदि से प्राप्त होते हैं।
डेटा अधिग्रहण प्रणाली के प्रकार
डाटा अधिग्रहण प्रणाली को निम्नलिखित में वर्गीकृत किया जा सकता है two types।
- एनालॉग डेटा अधिग्रहण प्रणाली
- डिजिटल डाटा अधिग्रहण प्रणाली
अब, हम एक-एक करके इन दो प्रकार के डेटा अधिग्रहण प्रणालियों के बारे में चर्चा करते हैं।
एनालॉग डेटा अधिग्रहण प्रणाली
डेटा अधिग्रहण प्रणाली, जिसे एनालॉग सिग्नल के साथ संचालित किया जा सकता है, के रूप में जाना जाता है analog data acquisition systems। निम्नलिखित एनालॉग डेटा अधिग्रहण प्रणाली के ब्लॉक हैं।
Transducer - यह भौतिक मात्राओं को विद्युत संकेतों में परिवर्तित करता है।
Signal conditioner - यह सिग्नल के वांछित हिस्से के प्रवर्धन और चयन जैसे कार्य करता है।
Display device - यह निगरानी उद्देश्य के लिए इनपुट संकेतों को प्रदर्शित करता है।
Graphic recording instruments - इनका उपयोग स्थायी रूप से इनपुट डेटा का रिकॉर्ड बनाने के लिए किया जा सकता है।
Magnetic tape instrumentation - इसका उपयोग इनपुट डेटा के अधिग्रहण, भंडारण और पुनरुत्पादन के लिए किया जाता है।
डिजिटल डाटा अधिग्रहण प्रणाली
डेटा अधिग्रहण प्रणाली, जिसे डिजिटल सिग्नल के साथ संचालित किया जा सकता है, के रूप में जाना जाता है digital data acquisition systems। इसलिए, वे सूचनाओं को संग्रहीत या प्रदर्शित करने के लिए डिजिटल घटकों का उपयोग करते हैं।
मुख्य रूप से, निम्नलिखित operations डिजिटल डेटा अधिग्रहण में जगह ले लो।
- एनालॉग सिग्नल का अधिग्रहण
- एनालॉग सिग्नल को डिजिटल सिग्नल या डिजिटल डेटा में बदलना
- डिजिटल सिग्नल या डिजिटल डेटा की प्रोसेसिंग
निम्नलिखित के ब्लॉक हैं Digital data acquisition systems।
Transducer - यह भौतिक मात्राओं को विद्युत संकेतों में परिवर्तित करता है।
Signal conditioner - यह सिग्नल के वांछित हिस्से के प्रवर्धन और चयन जैसे कार्य करता है।
Multiplexer- आउटपुट में कई इनपुट्स में से एक को जोड़ता है। तो, यह सीरियल कन्वर्टर के समानांतर काम करता है।
Analog to Digital Converter - यह एनालॉग इनपुट को अपने समकक्ष डिजिटल आउटपुट में परिवर्तित करता है।
Display device - यह डेटा को डिजिटल फॉर्मेट में प्रदर्शित करता है।
Digital Recorder - इसका उपयोग डेटा को डिजिटल प्रारूप में रिकॉर्ड करने के लिए किया जाता है।
बायोमेडिकल और एयरोस्पेस जैसे विभिन्न अनुप्रयोगों में डेटा अधिग्रहण प्रणाली का उपयोग किया जा रहा है। इसलिए, हम आवश्यकता के आधार पर या तो एनालॉग डेटा अधिग्रहण प्रणाली या डिजिटल डेटा अधिग्रहण प्रणाली चुन सकते हैं।