फजी लॉजिक - थ्योरी सेट करें
फ़ज़ी सेट को शास्त्रीय सेटों के विस्तार और सकल ओवरसिलेशन के रूप में माना जा सकता है। इसे सेट सदस्यता के संदर्भ में सबसे अच्छा समझा जा सकता है। मूल रूप से यह आंशिक सदस्यता की अनुमति देता है जिसका अर्थ है कि इसमें ऐसे तत्व शामिल हैं जिनकी सेट में सदस्यता की डिग्री बदलती है। इससे हम शास्त्रीय सेट और फ़ज़ी सेट के बीच के अंतर को समझ सकते हैं। शास्त्रीय सेट में ऐसे तत्व होते हैं जो सदस्यता के सटीक गुणों को संतुष्ट करते हैं जबकि फ़ज़ी सेट में ऐसे तत्व होते हैं जो सदस्यता के अभेद्य गुणों को संतुष्ट करते हैं।

गणितीय अवधारणा
सूचनाओं के ब्रह्मांड में $ $ $ $ $ \ "वाइडएटिल्डे सेट" को ऑर्डर किए गए जोड़े के सेट के रूप में परिभाषित किया जा सकता है और इसे गणितीय रूप से दर्शाया जा सकता है -
$$ \ widetilde {A} = \ left \ {\ left (y, \ mu _ {\ widetilde {A}} \ left (y \ right) \ right) | y \ _ U \ right \} $ $ में
यहाँ $ \ mu _ {\ widetilde {A}} \ left (y \ right) $ = $ की सदस्यता $ y $ in \ widetilde {A}, मान 0 से 1 तक की सीमा में मानती है, अर्थात, $ mu। _ {\ _ widetilde {A}} (y) \ in \ left [0,1 \ right] $।
फजी सेट का प्रतिनिधित्व
आइए अब हम जानकारी के ब्रह्मांड के दो मामलों पर विचार करते हैं और समझते हैं कि कैसे एक फजी सेट का प्रतिनिधित्व किया जा सकता है।
मामला एक
जब जानकारी का ब्रह्मांड $ U $ असतत और परिमित है -
$ $ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ फ़र्क {\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ = \ _ \ _ \ _ \ _ \ _ = \ _ \ _ \ _ \ _ \ _ = \ _ \ _ \ _ \ _ \ _ \ _ बटन = \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ बटन \ _ \ _ \ _ \ _ \ _ \ _ = \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ स्तन वाला लड़का लड़कियों के लिए $ $ \ " \ बायाँ (y_2 \ दाएँ)} {y_2} + \ frac {\ _ mu {{विधुतकांड {A}} \ बाएँ (y_3 \ दाएँ)} {y_3} + ... \ दाएँ \} $ $
$ = \ बाएँ \ {\ sum_ {i = 1} ^ {n} \ frac {\ _ mu _ {\ widetilde {A}} \ left (y_i \ right)} {y_i} \ right \} $
केस 2
जब जानकारी का ब्रह्मांड $ U $ निरंतर और अनंत हो -
$ $ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ & \ _ \ & \ _ \ & \ _ \ & ID & ID; $ $ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ = \ _ \ _ \ _ \ _ \ _ \ _ = \ _ \ _ \ _ \ _ \ _ \ चौड़ा = फिर से शुरू होना
उपरोक्त प्रतिनिधित्व में, संक्षेपण प्रतीक प्रत्येक तत्व के संग्रह का प्रतिनिधित्व करता है।
फजी सेट पर संचालन
दो फजी सेट होने से $ \ widetilde {A} $ और $ \ widetilde {B} $, जानकारी का ब्रह्मांड $ U $ और ब्रह्मांड का एक तत्व होता है, निम्नलिखित संबंध यूनियन, चौराहे और फजी सेट पर पूरक ऑपरेशन को व्यक्त करते हैं।
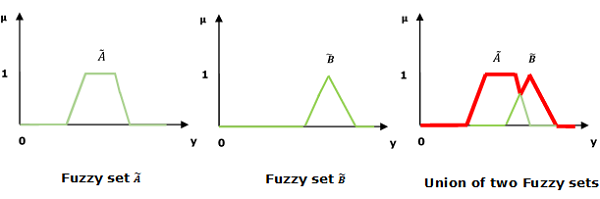
संघ / फ़ज़ी 'या'
आइए हम निम्नलिखित प्रतिनिधित्व पर विचार करें कि कैसे Union/Fuzzy ‘OR’ संबंध कार्य -
$ $ \ _ mu _ {{\ n विधवाएँ {A} \ cup \ widetilde {B}}} \ बाएँ (y \ दाएँ) = \ mu _ {\ _ चौड़ा करने वाले {A}} \ vee \ mu \ "विधुरवाहक {B} \ _ U $$ में quad \ forall y \
यहाँ '' अधिकतम 'ऑपरेशन का प्रतिनिधित्व करता है।
प्रतिच्छेदन / फजी 'और'
आइए हम निम्नलिखित प्रतिनिधित्व पर विचार करें कि कैसे Intersection/Fuzzy ‘AND’ संबंध कार्य -
$ $ \ _ mu _ {{\ n विधवाएँ {A} \ cap \ widetilde {B}}} \ _ बाएं (y \ दाएँ) = \ mu _ {\ _ चौड़ा करने वाले {A}} \ wedge \ mu \ "चौड़ी {{}} U $$ में quad \ forall y \
यहाँ '' मिनट 'ऑपरेशन का प्रतिनिधित्व करता है।

पूरक / फजी 'नहीं'
आइए हम निम्नलिखित प्रतिनिधित्व पर विचार करें कि कैसे Complement/Fuzzy ‘NOT’ संबंध कार्य -
$ $ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ & \ & ID & ID & ID; \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ & ID & CO & IN; US $ $ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ & & CO & gt; & \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ & & / ID & CO & CO; US $ $ $ $ के लिए $ $

फजी सेट के गुण
आइए हम फ़ज़ी सेट के विभिन्न गुणों पर चर्चा करें।
क्रमचयी गुणधर्म
दो फजी सेट होने पर $ \ widetilde {A} $ और $ \ widetilde {B} $, यह गुण हो जाता है -
$$ \ widetilde {A} \ cup \ widetilde {B} = \ widetilde {B} \ cup \ widetilde {A} $$
$$ \ widetilde {A} \ cap \ widetilde {B} = \ widetilde {B} \ cap \ widetilde {A} $ $
संबंधी संपत्ति
तीन फजी सेट होने पर $ \ widetilde {A} $, $ \ widetilde {B} $ और $ \ widetilde {C} $, यह गुण बताता है -
$ $ ((\ n \ _ \ _ \ _ \ _ \ / \ _}} \ _ \ / \ _ \ / \ _ \ / \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ 16 \ (\ n \ _ \ _ \ _ \ _ \ _ \ _ \ & \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ = \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _etetete) 15 $ के लिए $ $ $ {c}) $$
$ $ ((\ n चौड़ाई) {A} \ cap \ left \ widetilde {B}) \ cap \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {{}} \ right \ cap \ widetilde { सी}) $$
वितरण की जाने वाली संपत्ति
तीन फजी सेट होने पर $ \ widetilde {A} $, $ \ widetilde {B} $ और $ \ widetilde {C} $, यह गुण बताता है -
$$ \ widetilde {A} \ cup \ left (\ widetilde {B} \ cap \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cup \ widetilde ({}} \ right) \ cap \ left ((एक बहु-पक्षीय {A} \ cup \ widetilde {C} \ right) $$
$$ \ widetilde {A} \ cap \ left (\ widetilde {B} \ cup \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cap \ widetilde ({}} \ right) \ cup \ left ((एक विधुतक {A} \ cap \ widetilde {C} \ right) $$
आय सम्पत्ति
किसी भी फजी सेट के लिए $ \ widetilde {A} $, यह गुण बताता है -
$ $ \ "विधुतक {A} \ कप \ चौगुनी {ए} = = चौड़ी {{}}
$$ \ widetilde {A} \ cap \ widetilde {A} = \ widetilde {A} $ $
पहचान संपत्ति
फ़ज़ी सेट के लिए $ \ widetilde {A} $ और यूनिवर्सल सेट $ U $, यह गुण बताता है -
$$ \ widetilde {A} \ cup \ varphi = \ widetilde {A} $ $
$$ \ widetilde {A} \ cap U = \ widetilde {A} $ $
$$ \ widetilde {A} \ cap \ varphi = \ varphi $ $
$ $ \ "विधुतक {{}} कप U = U $ $
सकर्मक सम्पत्ति
तीन फजी सेट होने पर $ \ widetilde {A} $, $ \ widetilde {B} $ और $ \ widetilde {C} $, यह गुण बताता है -
$ $ If \: \ widetilde {A} \ subseteq \ widetilde {B} \ subseteq \ widetilde {C}, \: तो: \: \ widetilde {A} \ subseteq का चौड़ी {{}
इन्वॉल्वमेंट प्रॉपर्टी
किसी भी फजी सेट के लिए $ \ widetilde {A} $, यह गुण बताता है -
$$ \ overline {\ overline {\ widetilde {A}}} = \ widetilde {A} $ $
डी मॉर्गन का नियम
यह कानून तनातनी और विरोधाभास साबित करने में महत्वपूर्ण भूमिका निभाता है। यह कानून कहता है -
$$ \ overline {{\ widetilde {A} \ cap \ widetilde {B}} = = \ overline {\ widetilde {A}} \ cup \ overline {\ widetilde {B}}
$$ \ overline {{\ widetilde {A} \ cup \ widetilde {B}} = = \ overline {\ widetilde {A}} \ cap \ overline {\ widetilde {B}}