केरस - कन्वेंशन न्यूरल नेटवर्क
आइए हम MPL से मॉडल को संशोधित करते हैं Convolution Neural Network (CNN) हमारे पहले अंक पहचान समस्या के लिए।
सीएनएन का प्रतिनिधित्व नीचे दिया जा सकता है -
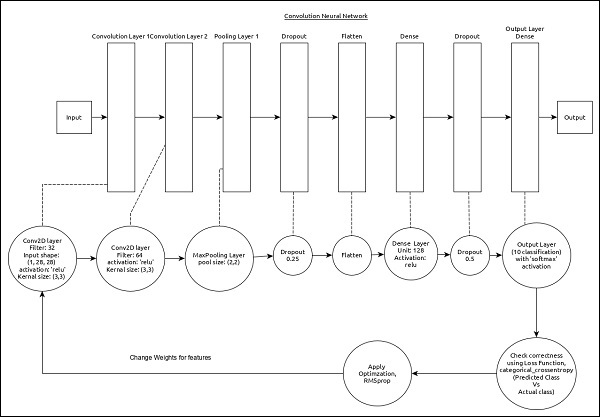
मॉडल की मुख्य विशेषताएं इस प्रकार हैं -
इनपुट परत में एक (1, 8, 28) मान होते हैं।
पहली सतह, Conv2D 32 फिल्टर और कर्नेल आकार के साथ 'रिले' सक्रियण फ़ंक्शन, (3,3) शामिल हैं।
दूसरी परत, Conv2D 64 फिल्टर और कर्नेल आकार के साथ 'रिले' सक्रियण फ़ंक्शन, (3,3) शामिल हैं।
पतली परत, MaxPooling पूल का आकार (2, 2) है।
पांचवीं परत, Flatten अपने सभी इनपुट को एकल आयाम में समतल करने के लिए उपयोग किया जाता है।
छठी परत, Dense 128 न्यूरॉन्स और 'रिले' सक्रियण समारोह के होते हैं।
सातवीं परत, Dropout इसके मान के रूप में 0.5 है।
आठवीं और अंतिम परत में 10 न्यूरॉन्स और 'सॉफ्टमैक्स' सक्रियण फ़ंक्शन होते हैं।
उपयोग categorical_crossentropy हानि समारोह के रूप में।
उपयोग Adadelta() ऑप्टिमाइज़र के रूप में।
उपयोग accuracy मैट्रिक्स के रूप में।
128 बैच आकार के रूप में उपयोग करें।
20 युगों के रूप में उपयोग करें।
Step 1 − Import the modules
हमें आवश्यक मॉड्यूल आयात करते हैं।
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
import numpy as npStep 2 − Load data
आइए हम mnist डेटासेट आयात करें।
(x_train, y_train), (x_test, y_test) = mnist.load_data()Step 3 − Process the data
हम अपने मॉडल के अनुसार डेटासेट बदलते हैं, ताकि यह हमारे मॉडल में फीड हो सके।
img_rows, img_cols = 28, 28
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)डेटा प्रोसेसिंग इनपुट डेटा और छवि प्रारूप कॉन्फ़िगरेशन के आकार को छोड़कर एमपीएल मॉडल के समान है।
Step 4 − Create the model
हमें वास्तविक मॉडल बनाते हैं।
model = Sequential()
model.add(Conv2D(32, kernel_size = (3, 3),
activation = 'relu', input_shape = input_shape))
model.add(Conv2D(64, (3, 3), activation = 'relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.25)) model.add(Flatten())
model.add(Dense(128, activation = 'relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation = 'softmax'))Step 5 − Compile the model
आइए हम चयनित नुकसान फ़ंक्शन, ऑप्टिमाइज़र और मैट्रिक्स का उपयोग करके मॉडल को संकलित करते हैं।
model.compile(loss = keras.losses.categorical_crossentropy,
optimizer = keras.optimizers.Adadelta(), metrics = ['accuracy'])Step 6 − Train the model
आइए हम मॉडल का उपयोग करके प्रशिक्षित करें fit() तरीका।
model.fit(
x_train, y_train,
batch_size = 128,
epochs = 12,
verbose = 1,
validation_data = (x_test, y_test)
)एप्लिकेशन को निष्पादित करने से नीचे दी गई जानकारी का उत्पादन होगा -
Train on 60000 samples, validate on 10000 samples Epoch 1/12
60000/60000 [==============================] - 84s 1ms/step - loss: 0.2687
- acc: 0.9173 - val_loss: 0.0549 - val_acc: 0.9827 Epoch 2/12
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0899
- acc: 0.9737 - val_loss: 0.0452 - val_acc: 0.9845 Epoch 3/12
60000/60000 [==============================] - 83s 1ms/step - loss: 0.0666
- acc: 0.9804 - val_loss: 0.0362 - val_acc: 0.9879 Epoch 4/12
60000/60000 [==============================] - 81s 1ms/step - loss: 0.0564
- acc: 0.9830 - val_loss: 0.0336 - val_acc: 0.9890 Epoch 5/12
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0472
- acc: 0.9861 - val_loss: 0.0312 - val_acc: 0.9901 Epoch 6/12
60000/60000 [==============================] - 83s 1ms/step - loss: 0.0414
- acc: 0.9877 - val_loss: 0.0306 - val_acc: 0.9902 Epoch 7/12
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0375
-acc: 0.9883 - val_loss: 0.0281 - val_acc: 0.9906 Epoch 8/12
60000/60000 [==============================] - 91s 2ms/step - loss: 0.0339
- acc: 0.9893 - val_loss: 0.0280 - val_acc: 0.9912 Epoch 9/12
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0325
- acc: 0.9901 - val_loss: 0.0260 - val_acc: 0.9909 Epoch 10/12
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0284
- acc: 0.9910 - val_loss: 0.0250 - val_acc: 0.9919 Epoch 11/12
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0287
- acc: 0.9907 - val_loss: 0.0264 - val_acc: 0.9916 Epoch 12/12
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0265
- acc: 0.9920 - val_loss: 0.0249 - val_acc: 0.9922Step 7 − Evaluate the model
आइए हम परीक्षण डेटा का उपयोग करके मॉडल का मूल्यांकन करें।
score = model.evaluate(x_test, y_test, verbose = 0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])उपरोक्त कोड को निष्पादित करने से निम्न जानकारी उत्पन्न होगी -
Test loss: 0.024936060590433316
Test accuracy: 0.9922परीक्षण की सटीकता 99.22% है। हमने लिखावट अंकों की पहचान करने के लिए एक सर्वश्रेष्ठ मॉडल बनाया है।
Step 8 − Predict
अंत में, नीचे दिए गए चित्रों से अंक की भविष्यवाणी करें -
pred = model.predict(x_test)
pred = np.argmax(pred, axis = 1)[:5]
label = np.argmax(y_test,axis = 1)[:5]
print(pred)
print(label)उपरोक्त एप्लिकेशन का आउटपुट निम्नानुसार है -
[7 2 1 0 4]
[7 2 1 0 4]दोनों सरणी का आउटपुट समान है और यह दर्शाता है कि हमारा मॉडल सही ढंग से पहले पांच छवियों की भविष्यवाणी करता है।