प्रतिगमन एल्गोरिदम - रैखिक प्रतिगमन
रैखिक प्रतिगमन का परिचय
रैखिक प्रतिगमन को सांख्यिकीय मॉडल के रूप में परिभाषित किया जा सकता है जो स्वतंत्र चर के सेट के साथ एक आश्रित चर के बीच रैखिक संबंध का विश्लेषण करता है। चर के बीच रैखिक संबंध का मतलब है कि जब एक या अधिक स्वतंत्र चर का मूल्य बदल जाएगा (वृद्धि या कमी), तो निर्भर चर का मूल्य भी तदनुसार (वृद्धि या कमी) बदल जाएगा।
गणितीय रूप से संबंध को निम्नलिखित समीकरण की सहायता से दर्शाया जा सकता है -
वाई = एमएक्स + बी
यहाँ, Y आश्रित चर है जिसका हम अनुमान लगाने की कोशिश कर रहे हैं
एक्स आश्रित चर है जिसका हम भविष्यवाणियां करने के लिए उपयोग कर रहे हैं।
मीटर प्रतिगमन रेखा का ढलान है जो X पर Y के प्रभाव का प्रतिनिधित्व करता है
b एक स्थिरांक है, जिसे Y- इंटरसेप्ट के रूप में जाना जाता है। यदि X = 0, Y, b के बराबर होता।
इसके अलावा, रैखिक संबंध प्रकृति में सकारात्मक या नकारात्मक हो सकता है जैसा कि नीचे बताया गया है -
सकारात्मक रैखिक संबंध
यदि स्वतंत्र और आश्रित चर दोनों बढ़ जाते हैं तो एक रैखिक संबंध को सकारात्मक कहा जाएगा। इसे निम्नलिखित ग्राफ की मदद से समझा जा सकता है -

नकारात्मक रैखिक संबंध
यदि स्वतंत्र वृद्धि और निर्भर चर कम हो जाता है तो एक रैखिक संबंध को सकारात्मक कहा जाएगा। इसे निम्नलिखित ग्राफ की मदद से समझा जा सकता है -

रैखिक प्रतिगमन के प्रकार
रैखिक प्रतिगमन निम्नलिखित दो प्रकार के होते हैं -
- सरल रैखिक प्रतिगमन
- एकाधिक रेखीय प्रतिगमन
सरल रैखिक प्रतिगमन (एसएलआर)
यह रैखिक प्रतिगमन का सबसे बुनियादी संस्करण है जो एक एकल सुविधा का उपयोग करके प्रतिक्रिया की भविष्यवाणी करता है। एसएलआर में धारणा यह है कि दो चर रैखिक रूप से संबंधित हैं।
पायथन कार्यान्वयन
हम पायथन में एसएलआर को दो तरीकों से लागू कर सकते हैं, एक है अपने स्वयं के डाटासेट को उपलब्ध कराना और दूसरा है स्किटिट-लर्निंग पाइथन लाइब्रेरी से डेटासेट का उपयोग करना।
Example 1 - निम्नलिखित पायथन कार्यान्वयन उदाहरण में, हम अपने स्वयं के डेटासेट का उपयोग कर रहे हैं।
सबसे पहले, हम आवश्यक पैकेजों को निम्नानुसार शुरू करेंगे -
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltअगला, एक फ़ंक्शन परिभाषित करें जो SLR के लिए महत्वपूर्ण मानों की गणना करेगा -
def coef_estimation(x, y):निम्नलिखित स्क्रिप्ट लाइन टिप्पणियों की संख्या n देगी -
n = np.size(x)X और y वेक्टर के माध्य की गणना निम्नानुसार की जा सकती है -
m_x, m_y = np.mean(x), np.mean(y)हम एक्स के बारे में क्रॉस-विचलन और विचलन इस प्रकार पा सकते हैं -
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xअगला, प्रतिगमन गुणांक अर्थात बी की गणना निम्नानुसार की जा सकती है -
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)अगला, हमें एक फ़ंक्शन को परिभाषित करने की आवश्यकता है जो प्रतिगमन रेखा को साजिश करेगा और साथ ही प्रतिक्रिया वेक्टर की भविष्यवाणी करेगा -
def plot_regression_line(x, y, b):निम्न स्क्रिप्ट लाइन स्कैटर प्लॉट के रूप में वास्तविक बिंदुओं की साजिश करेगी -
plt.scatter(x, y, color = "m", marker = "o", s = 30)निम्नलिखित स्क्रिप्ट लाइन प्रतिक्रिया वेक्टर की भविष्यवाणी करेगी -
y_pred = b[0] + b[1]*xनिम्नलिखित स्क्रिप्ट लाइनें प्रतिगमन रेखा को प्लॉट करेंगी और उन पर लेबल लगाएंगी -
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()अंत में, हमें मुख्य कार्य को परिभाषित करने की आवश्यकता है (उपयोक्ता को परिभाषित करने के लिए और उपर्युक्त फ़ंक्शन को कॉल करने के लिए -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()उत्पादन
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788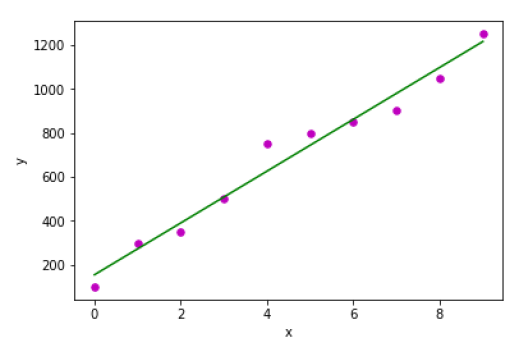
Example 2 - निम्नलिखित पायथन कार्यान्वयन उदाहरण में, हम स्किकिट-लर्न से डायबिटीज डेटासेट का उपयोग कर रहे हैं।
सबसे पहले, हम आवश्यक पैकेजों को निम्नानुसार शुरू करेंगे -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreअगला, हम डायबिटीज डेटासेट को लोड करेंगे और उसकी वस्तु बनाएंगे -
diabetes = datasets.load_diabetes()जैसा कि हम एसएलआर को लागू कर रहे हैं, हम निम्नानुसार केवल एक ही सुविधा का उपयोग करेंगे -
X = diabetes.data[:, np.newaxis, 2]इसके बाद, हमें डेटा को प्रशिक्षण और परीक्षण सेट में विभाजित करने की आवश्यकता है -
X_train = X[:-30]
X_test = X[-30:]इसके बाद, हमें लक्ष्य को प्रशिक्षण और परीक्षण सेटों में विभाजित करने की आवश्यकता है -
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]अब, मॉडल को प्रशिक्षित करने के लिए हमें रेखीय प्रतिगमन ऑब्जेक्ट बनाने की आवश्यकता है -
regr = linear_model.LinearRegression()अगला, प्रशिक्षण सेट का उपयोग करके मॉडल को निम्नानुसार प्रशिक्षित करें -
regr.fit(X_train, y_train)अगला, निम्नानुसार परीक्षण सेट का उपयोग करके भविष्यवाणियां करें -
y_pred = regr.predict(X_test)इसके बाद, हम कुछ गुणांक जैसे कि MSE, Variance स्कोर आदि को प्रिंट करेंगे।
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))अब, आउटपुट को निम्नानुसार प्लॉट करें -
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()उत्पादन
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
एकाधिक रैखिक प्रतिगमन (MLR)
यह सरल रैखिक प्रतिगमन का विस्तार है जो दो या दो से अधिक विशेषताओं का उपयोग करके प्रतिक्रिया की भविष्यवाणी करता है। गणितीय रूप से हम इसे इस प्रकार समझा सकते हैं -
एक प्रेक्षणों पर विचार करें, जिसमें n अवलोकनों, पी विशेषताओं अर्थात स्वतंत्र चर और y को एक प्रतिक्रिया के रूप में या निर्भर चर के रूप में p सुविधाओं के लिए प्रतिगमन लाइन की गणना निम्नानुसार की जा सकती है -
$$ ज (x_ {मैं}) = b_ {0} + b_ {1} {x_ i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {आईपी} $$यहाँ, h (x i ) अनुमानित प्रतिक्रिया मान है और b 0 , b 1 , b 2 …, b p प्रतिगमन गुणांक हैं।
एकाधिक रैखिक प्रतिगमन मॉडल में हमेशा अवशिष्ट त्रुटि के रूप में जाना जाता डेटा में त्रुटियां शामिल होती हैं जो गणना को निम्नानुसार बदलती हैं -
$$ ज (x_ {मैं}) = b_ {0} + b_ {1} {x_ i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {आईपी} + E_ {मैं} $$हम उपरोक्त समीकरण भी इस प्रकार लिख सकते हैं -
$ $ y_ {i} = h (x_ {i}) + e_ {i} \: या:: e_ {i} = y_ {i} - h (x_ {i}) $$पायथन कार्यान्वयन
इस उदाहरण में, हम scikit से बोस्टन हाउसिंग डेटासेट का उपयोग करेंगे -
सबसे पहले, हम आवश्यक पैकेजों को निम्नानुसार शुरू करेंगे -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsअगला, डेटासेट निम्नानुसार लोड करें -
boston = datasets.load_boston(return_X_y=False)निम्नलिखित स्क्रिप्ट लाइनें सुविधा मैट्रिक्स, एक्स और प्रतिक्रिया वेक्टर, वाई - को परिभाषित करेंगी
X = boston.data
y = boston.targetइसके बाद, डेटासेट को प्रशिक्षण और परीक्षण सेटों में विभाजित करें:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)उदाहरण
अब, रैखिक प्रतिगमन ऑब्जेक्ट बनाएं और मॉडल को निम्नानुसार प्रशिक्षित करें -
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()उत्पादन
Coefficients:
[
-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01
]
Variance score: 0.709454060230326
मान्यताओं
निम्नलिखित डेटासेट के बारे में कुछ धारणाएँ हैं जो रैखिक प्रतिगमन मॉडल द्वारा बनाई गई हैं -
Multi-collinearity- रेखीय प्रतिगमन मॉडल मानता है कि डेटा में बहुत कम या कोई बहु-संप्रभुता नहीं है। मूल रूप से, बहु-संप्रभुता तब होती है जब स्वतंत्र चर या विशेषताओं में निर्भरता होती है।
Auto-correlation- एक अन्य धारणा रैखिक प्रतिगमन मॉडल मानती है कि डेटा में बहुत कम या कोई ऑटो-सहसंबंध नहीं है। मूल रूप से, ऑटो-सहसंबंध तब होता है जब अवशिष्ट त्रुटियों के बीच निर्भरता होती है।
Relationship between variables - रैखिक प्रतिगमन मॉडल मानता है कि प्रतिक्रिया और सुविधा चर के बीच संबंध रैखिक होना चाहिए।