ग्राफ एल्गोरिथ्म
एक ग्राफ एक अमूर्त संकेतन है जिसका उपयोग वस्तुओं के जोड़े के बीच संबंध को दर्शाने के लिए किया जाता है। एक ग्राफ के होते हैं -
Vertices- एक ग्राफ में परस्पर जुड़ी वस्तुओं को कोने कहा जाता है। कार्यक्षेत्र के रूप में भी जाना जाता हैnodes।
Edges - किनारे वे लिंक होते हैं जो कोने जोड़ते हैं।
रेखांकन दो प्रकार के होते हैं -
Directed graph - एक निर्देशित ग्राफ में, किनारों की दिशा होती है, यानी, किनारों को एक शीर्ष से दूसरे तक जाना होता है।
Undirected graph - एक अप्रत्यक्ष ग्राफ में, किनारों की कोई दिशा नहीं है।
ग्राफ रंग
ग्राफ रंग एक ग्राफ के शीर्षों पर रंगों को असाइन करने की एक विधि है ताकि किसी भी दो आसन्न कोने में एक ही रंग न हो। रंग भरने की कुछ समस्याएं हैं -
Vertex coloring - एक ग्राफ के शीर्षों को रंगने का एक तरीका ताकि कोई भी दो आसन्न कोने समान रंग साझा न करें।
Edge Coloring - यह प्रत्येक किनारे पर एक रंग निर्दिष्ट करने की विधि है ताकि किसी भी दो किनारों पर समान रंग न हो।
Face coloring - यह प्रत्येक चेहरे या एक प्लांटर ग्राफ के क्षेत्र को एक रंग प्रदान करता है ताकि कोई भी दो चेहरे जो एक समान सीमा साझा करते हैं, उनका रंग एक ही हो।
क्रोमेटिक नंबर
रंगीन संख्या एक ग्राफ को रंग देने के लिए आवश्यक रंगों की न्यूनतम संख्या है। उदाहरण के लिए, निम्नलिखित ग्राफ की रंगीन संख्या 3 है।

ग्राफ रंगाई की अवधारणा को समय सारिणी, मोबाइल रेडियो फ्रीक्वेंसी असाइनमेंट, सूडुकू, रजिस्टर आवंटन, और मानचित्रों के रंग तैयार करने में लागू किया जाता है।
ग्राफ रंग के लिए कदम
प्रत्येक प्रोसेसर के प्रारंभिक मूल्य को n-आयामी सरणी में 1 पर सेट करें।
अब एक शीर्ष पर एक विशेष रंग को असाइन करने के लिए, यह निर्धारित करें कि क्या रंग पहले से ही आसन्न कोने को सौंपा गया है या नहीं।
यदि कोई प्रोसेसर आसन्न कोने में समान रंग का पता लगाता है, तो वह सरणी में 0 पर अपना मान सेट करता है।
एन 2 तुलना करने के बाद , यदि सरणी का कोई भी तत्व 1 है, तो यह एक वैध रंग है।
ग्राफ़ के रंग के लिए स्यूडोकोड
begin
create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
status[i0,..in-1] = 1
for j varies from 0 to n-1 do
begin
for k varies from 0 to n-1 do
begin
if aj,k=1 and ij=ikthen
status[i0,..in-1] =0
end
end
ok = ΣStatus
if ok > 0, then display valid coloring exists
else
display invalid coloring
endन्यूनतम स्पैनिंग ट्री
एक फैले हुए वृक्ष, जिसके सभी किनारों पर वजन (या लंबाई) का योग ग्राफ G के सभी अन्य संभावित फैले हुए पेड़ों से कम है minimal spanning tree या minimum cost spanningपेड़। निम्नलिखित आंकड़ा एक भारित जुड़ा हुआ ग्राफ दिखाता है।

उपरोक्त ग्राफ के कुछ संभावित फैले हुए पेड़ों को नीचे दिखाया गया है -



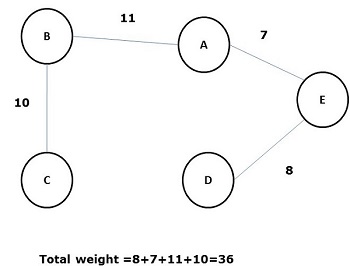



उपरोक्त सभी फैले हुए वृक्षों में, आकृति (d) न्यूनतम फैले हुए वृक्ष हैं। ट्रैवलिंग सेल्समैन समस्या में न्यूनतम लागत वाले फैले पेड़ की अवधारणा को लागू किया जाता है, इलेक्ट्रॉनिक सर्किट डिजाइन करना, कुशल नेटवर्क डिजाइन करना और कुशल मार्ग एल्गोरिदम डिजाइन करना।
न्यूनतम लागत फैले पेड़ को लागू करने के लिए, निम्नलिखित दो विधियों का उपयोग किया जाता है -
- प्राइम का एल्गोरिथम
- क्रुसकल का एल्गोरिथम
प्राइम का एल्गोरिथम
प्राइम का एल्गोरिथ्म एक लालची एल्गोरिथ्म है, जो हमें एक भारित अप्रत्यक्ष ग्राफ के लिए न्यूनतम फैले हुए पेड़ को खोजने में मदद करता है। यह पहले एक शीर्ष का चयन करता है और उस शीर्ष पर सबसे कम वजन घटना के साथ एक बढ़त पाता है।
प्राइम के एल्गोरिथम के चरण
किसी भी शीर्ष का चयन करें, ग्राफ़ G का v 1 कहें ।
बढ़त का चयन करें, ई का कहना है 1 जी की ऐसी है कि ई 1 = वी 1 वी 2 और वी 1 ≠ वी 2 और ई 1 वी पर किनारों घटना में कम से कम वजन है 1 ग्राफ जी में
अब, चरण 2 के बाद, वी 2 पर न्यूनतम भारित बढ़त घटना का चयन करें ।
इसे जारी रखें जब तक n-1 किनारों को चुना नहीं गया है। यहाँn कोने की संख्या है।

न्यूनतम फैले पेड़ है -

क्रुसकल का एल्गोरिथम
क्रुस्कल का एल्गोरिथ्म एक लालची एल्गोरिथ्म है, जो हमें एक जुड़े हुए भारित ग्राफ के लिए न्यूनतम फैले हुए पेड़ को खोजने में मदद करता है, जिससे प्रत्येक चरण पर बढ़ती लागत आर्क्स मिलती है। यह एक न्यूनतम-फैले पेड़ के एल्गोरिथ्म है जो कम से कम संभव वजन का एक किनारा पाता है जो जंगल में किसी भी दो पेड़ों को जोड़ता है।
क्रुशाल के एल्गोरिथ्म के चरण
न्यूनतम वजन के एक किनारे का चयन करें; कहते हैं ई 1 ग्राफ़ जी के और ई 1 एक पाश नहीं है।
ई 1 से जुड़ा अगला न्यूनतम भारित किनारा चुनें ।
इसे जारी रखें जब तक n-1 किनारों को चुना नहीं गया है। यहाँn कोने की संख्या है।

उपरोक्त ग्राफ का न्यूनतम फैले हुए पेड़ है -
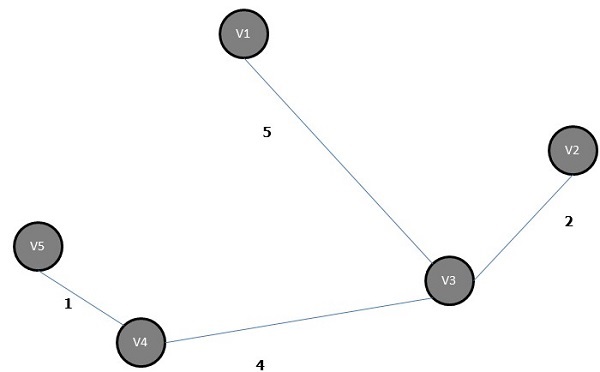
सबसे छोटा पथ एल्गोरिथम
सबसे छोटा पथ एल्गोरिथ्म स्रोत नोड (S) से गंतव्य नोड (D) तक कम से कम लागत पथ खोजने की एक विधि है। यहां, हम मूर के एल्गोरिथ्म पर चर्चा करेंगे, जिसे चौड़ाई प्रथम खोज एल्गोरिदम के रूप में भी जाना जाता है।
मूर की एल्गोरिथ्म
स्रोत शीर्ष, S लेबल करें और इसे लेबल करें i और सेट करें i=0।
शीर्ष पर लेबल किए गए शीर्ष के सभी गैर-लंबित वर्जन ज्ञात करें i। यदि कोई कोने वर्टेक्स से नहीं जुड़े हैं, तो S, तो D, S से कनेक्ट नहीं है। यदि एस से जुड़े कोने हैं, तो उन्हें लेबल करेंi+1।
यदि D लेबल है, तो चरण 4 पर जाएं, अन्यथा i = i + 1 को बढ़ाने के लिए चरण 2 पर जाएं।
सबसे छोटा रास्ता मिलने के बाद रुकें।