समानांतर एल्गोरिथम - त्वरित गाइड
एक algorithmचरणों का एक क्रम है जो उपयोगकर्ता से इनपुट लेता है और कुछ गणना के बाद, एक आउटपुट का उत्पादन करता है। एparallel algorithm एक एल्गोरिथ्म है जो विभिन्न प्रसंस्करण उपकरणों पर एक साथ कई निर्देशों को निष्पादित कर सकता है और फिर अंतिम परिणाम का उत्पादन करने के लिए सभी व्यक्तिगत आउटपुट को जोड़ सकता है।
समवर्ती प्रसंस्करण
इंटरनेट की वृद्धि के साथ-साथ कंप्यूटर की आसान उपलब्धता ने हमारे डेटा को स्टोर और प्रोसेस करने के तरीके को बदल दिया है। हम एक ऐसे दिन और उम्र में जी रहे हैं, जहां डेटा प्रचुर मात्रा में उपलब्ध है। हर दिन हम डेटा की बड़ी मात्रा से निपटते हैं, जिसके लिए जटिल कंप्यूटिंग की आवश्यकता होती है और वह भी त्वरित समय में। कभी-कभी, हमें एक साथ होने वाली समान या परस्पर संबंधित घटनाओं से डेटा प्राप्त करने की आवश्यकता होती है। यह वह जगह है जहाँ हमें आवश्यकता होती हैconcurrent processing यह एक जटिल कार्य को विभाजित कर सकता है और त्वरित समय में आउटपुट का उत्पादन करने के लिए इसे कई प्रणालियों को संसाधित कर सकता है।
समवर्ती प्रसंस्करण आवश्यक है जहां कार्य में जटिल डेटा का एक बड़ा प्रसंस्करण शामिल है। उदाहरणों में शामिल हैं - बड़े डेटाबेस तक पहुँच, विमान परीक्षण, खगोलीय गणना, परमाणु और परमाणु भौतिकी, बायोमेडिकल विश्लेषण, आर्थिक नियोजन, छवि प्रसंस्करण, रोबोटिक्स, मौसम पूर्वानुमान, वेब-आधारित सेवाएं, आदि।
समानांतरवाद क्या है?
Parallelismएक साथ कई निर्देशों को सेट करने की प्रक्रिया है। यह कुल कम्प्यूटेशनल समय को कम करता है। समानांतरवाद का उपयोग करके लागू किया जा सकता हैparallel computers,यानी कई प्रोसेसर वाला कंप्यूटर। समानांतर कंप्यूटरों को समानांतर एल्गोरिथम, प्रोग्रामिंग लैंग्वेज, कंपाइलर और ऑपरेटिंग सिस्टम की आवश्यकता होती है जो मल्टीटास्किंग का समर्थन करते हैं।
इस ट्यूटोरियल में, हम केवल इसके बारे में चर्चा करेंगे parallel algorithms। आगे बढ़ने से पहले, आइए हम पहले एल्गोरिदम और उनके प्रकारों के बारे में चर्चा करें।
एक एल्गोरिथ्म क्या है?
एक algorithmकिसी समस्या को हल करने के लिए निर्देशों का एक क्रम है। एल्गोरिथ्म डिजाइन करते समय, हमें कंप्यूटर की वास्तुकला पर विचार करना चाहिए, जिस पर एल्गोरिथ्म को निष्पादित किया जाएगा। वास्तुकला के अनुसार, कंप्यूटर दो प्रकार के होते हैं -
- अनुक्रमिक कंप्यूटर
- समानांतर कंप्यूटर
कंप्यूटर की वास्तुकला के आधार पर, हमारे पास दो प्रकार के एल्गोरिदम हैं -
Sequential Algorithm - एक एल्गोरिथ्म जिसमें किसी समस्या को हल करने के लिए कालानुक्रमिक क्रम में निर्देशों के कुछ लगातार चरणों को निष्पादित किया जाता है।
Parallel Algorithm- समस्या को उप-समस्याओं में विभाजित किया गया है और व्यक्तिगत आउटपुट प्राप्त करने के लिए समानांतर में निष्पादित किया जाता है। बाद में, इन व्यक्तिगत आउटपुट को अंतिम वांछित आउटपुट प्राप्त करने के लिए एक साथ जोड़ा जाता है।
एक बड़ी समस्या को विभाजित करना आसान नहीं है sub-problems। उप-समस्याओं में उनके बीच डेटा निर्भरता हो सकती है। इसलिए, प्रोसेसर को समस्या को हल करने के लिए एक दूसरे के साथ संवाद करना पड़ता है।
यह पता चला है कि प्रोसेसर द्वारा एक-दूसरे के साथ संचार करने में आवश्यक समय वास्तविक प्रसंस्करण समय से अधिक है। इसलिए, समानांतर एल्गोरिदम को डिजाइन करते समय, एक कुशल एल्गोरिथ्म प्राप्त करने के लिए उचित सीपीयू उपयोग पर विचार किया जाना चाहिए।
एक एल्गोरिथ्म को ठीक से डिजाइन करने के लिए, हमारे पास मूल का स्पष्ट विचार होना चाहिए model of computation एक समानांतर कंप्यूटर में।
संगणना का मॉडल
दोनों अनुक्रमिक और समानांतर कंप्यूटर एल्गोरिदम नामक निर्देशों के एक सेट (धारा) पर काम करते हैं। निर्देशों का ये सेट (एल्गोरिथम) कंप्यूटर को निर्देश देता है कि उसे प्रत्येक चरण में क्या करना है।
निर्देश धारा और डेटा स्ट्रीम के आधार पर, कंप्यूटर को चार श्रेणियों में वर्गीकृत किया जा सकता है -
- सिंगल इंस्ट्रक्शन स्ट्रीम, सिंगल डेटा स्ट्रीम (SISD) कंप्यूटर
- एकल निर्देश धारा, एकाधिक डेटा स्ट्रीम (SIMD) कंप्यूटर
- मल्टीपल इंस्ट्रक्शन स्ट्रीम, सिंगल डेटा स्ट्रीम (MISD) कंप्यूटर
- मल्टीपल इंस्ट्रक्शन स्ट्रीम, मल्टीपल डेटा स्ट्रीम (MIMD) कंप्यूटर
SISD कंप्यूटर
SISD कंप्यूटर में होते हैं one control unit, one processing unit, तथा one memory unit।

इस प्रकार के कंप्यूटरों में, प्रोसेसर कंट्रोल यूनिट से निर्देशों की एक एकल स्ट्रीम प्राप्त करता है और मेमोरी यूनिट से डेटा की एक एकल स्ट्रीम पर संचालित होता है। गणना के दौरान, प्रत्येक चरण पर, प्रोसेसर नियंत्रण इकाई से एक निर्देश प्राप्त करता है और मेमोरी यूनिट से प्राप्त एकल डेटा पर संचालित होता है।
SIMD कंप्यूटर
SIMD कंप्यूटर में होते हैं one control unit, multiple processing units, तथा shared memory or interconnection network।
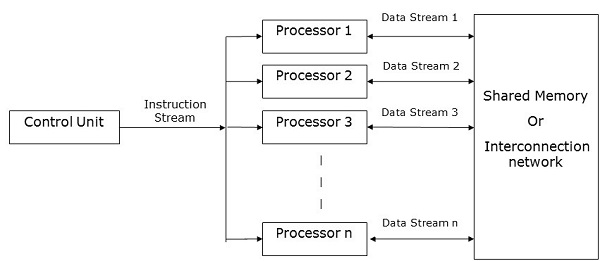
यहां, एक एकल नियंत्रण इकाई सभी प्रसंस्करण इकाइयों को निर्देश भेजती है। गणना के दौरान, प्रत्येक चरण पर, सभी प्रोसेसर नियंत्रण इकाई से निर्देशों का एक सेट प्राप्त करते हैं और मेमोरी यूनिट से डेटा के विभिन्न सेट पर काम करते हैं।
प्रत्येक प्रोसेसिंग यूनिट में डेटा और निर्देश दोनों को स्टोर करने के लिए अपनी स्थानीय मेमोरी यूनिट होती है। SIMD कंप्यूटर में, प्रोसेसर को आपस में संवाद करने की आवश्यकता होती है। इसके द्वारा किया जाता हैshared memory या द्वारा interconnection network।
जबकि कुछ प्रोसेसर निर्देशों का एक सेट निष्पादित करते हैं, शेष प्रोसेसर अपने अगले निर्देशों के लिए प्रतीक्षा करते हैं। कंट्रोल यूनिट के निर्देश तय करते हैं कि कौन सा प्रोसेसर होगाactive (निर्देशों को निष्पादित) या inactive (अगले निर्देश की प्रतीक्षा करें)
MISD कंप्यूटर
जैसा कि नाम से पता चलता है, MISD कंप्यूटर में होते हैं multiple control units, multiple processing units, तथा one common memory unit।

यहां, प्रत्येक प्रोसेसर की अपनी नियंत्रण इकाई है और वे एक साझा मेमोरी यूनिट साझा करते हैं। सभी प्रोसेसरों को अपनी-अपनी नियंत्रण इकाई से व्यक्तिगत रूप से निर्देश मिलते हैं और वे अपने संबंधित नियंत्रण इकाइयों से प्राप्त निर्देशों के अनुसार डेटा की एक ही धारा पर काम करते हैं। यह प्रोसेसर एक साथ संचालित होता है।
MIMD कंप्यूटर
MIMD कंप्यूटर हैं multiple control units, multiple processing units, और एक shared memory या interconnection network।

यहां, प्रत्येक प्रोसेसर की अपनी नियंत्रण इकाई, स्थानीय मेमोरी यूनिट और अंकगणित और तर्क इकाई है। वे अपने संबंधित नियंत्रण इकाइयों से निर्देशों के विभिन्न सेट प्राप्त करते हैं और डेटा के विभिन्न सेटों पर काम करते हैं।
ध्यान दें
एक MIMD कंप्यूटर जो एक आम मेमोरी साझा करता है, के रूप में जाना जाता है multiprocessors, जबकि जो आपस में जुड़ने वाले नेटवर्क का उपयोग करते हैं उन्हें जाना जाता है multicomputers।
प्रोसेसर की भौतिक दूरी के आधार पर, मल्टीकॉमपावर दो प्रकार के होते हैं -
Multicomputer - जब सभी प्रोसेसर एक दूसरे के बहुत करीब होते हैं (जैसे, एक ही कमरे में)।
Distributed system - जब सभी प्रोसेसर एक दूसरे से बहुत दूर हों (जैसे- अलग-अलग शहरों में)
एक एल्गोरिथ्म का विश्लेषण हमें यह निर्धारित करने में मदद करता है कि एल्गोरिथ्म उपयोगी है या नहीं। आमतौर पर, एक एल्गोरिथ्म का विश्लेषण उसके निष्पादन समय के आधार पर किया जाता है(Time Complexity) और अंतरिक्ष की मात्रा (Space Complexity) इसकी जरूरत है।
चूँकि हमारे पास परिष्कृत मेमोरी डिवाइस उचित कीमत पर उपलब्ध हैं, इसलिए भंडारण स्थान अब कोई समस्या नहीं है। इसलिए, अंतरिक्ष जटिलता को इतना महत्व नहीं दिया जाता है।
समानांतर एल्गोरिदम को कंप्यूटर की गणना की गति में सुधार करने के लिए डिज़ाइन किया गया है। समानांतर एल्गोरिदम का विश्लेषण करने के लिए, हम आम तौर पर निम्नलिखित मापदंडों पर विचार करते हैं -
- समय जटिलता (निष्पादन समय),
- उपयोग किए गए प्रोसेसर की कुल संख्या, और
- कुल लागत।
समय जटिलता
समानांतर एल्गोरिदम विकसित करने के पीछे मुख्य कारण एक एल्गोरिथ्म की गणना समय को कम करना था। इस प्रकार, एक एल्गोरिथ्म के निष्पादन समय का मूल्यांकन इसकी दक्षता का विश्लेषण करने में बेहद महत्वपूर्ण है।
किसी समस्या को हल करने के लिए एल्गोरिथ्म द्वारा लिए गए समय के आधार पर निष्पादन का समय मापा जाता है। कुल निष्पादन समय की गणना उस क्षण से की जाती है जब एल्गोरिथ्म उस पल को निष्पादित करना शुरू कर देता है जो इसे बंद कर देता है। यदि सभी प्रोसेसर एक ही समय में निष्पादन शुरू या समाप्त नहीं करते हैं, तो एल्गोरिथ्म का कुल निष्पादन समय वह क्षण होता है जब पहला प्रोसेसर उस क्षण के लिए अपना निष्पादन शुरू करता है जब अंतिम प्रोसेसर अपना निष्पादन रोक देता है।
एक एल्गोरिथ्म की समय जटिलता को तीन श्रेणियों में वर्गीकृत किया जा सकता है
Worst-case complexity - जब किसी दिए गए इनपुट के लिए एल्गोरिदम द्वारा आवश्यक समय की मात्रा होती है maximum।
Average-case complexity - जब किसी दिए गए इनपुट के लिए एल्गोरिदम द्वारा आवश्यक समय की मात्रा होती है average।
Best-case complexity - जब किसी दिए गए इनपुट के लिए एल्गोरिदम द्वारा आवश्यक समय की मात्रा होती है minimum।
असममित विश्लेषण
एक एल्गोरिथ्म की जटिलता या दक्षता वांछित आउटपुट प्राप्त करने के लिए एल्गोरिदम द्वारा निष्पादित चरणों की संख्या है। अपने सैद्धांतिक विश्लेषण में एक एल्गोरिथ्म की जटिलता की गणना करने के लिए असममित विश्लेषण किया जाता है। असममित विश्लेषण में, एल्गोरिथ्म की जटिलता फ़ंक्शन की गणना करने के लिए इनपुट की एक बड़ी लंबाई का उपयोग किया जाता है।
Note - Asymptoticएक ऐसी स्थिति है जहां एक रेखा वक्र से मिलने के लिए झुकती है, लेकिन वे प्रतिच्छेद नहीं करती हैं। यहाँ रेखा और वक्र एक दूसरे के लिए विषम है।
गति के लिए उच्च सीमा और कम सीमा का उपयोग करके एल्गोरिथ्म के लिए सबसे तेज़ और सबसे संभव निष्पादन समय का वर्णन करने का सबसे आसान तरीका एसिम्पोटिक है। इसके लिए, हम निम्नलिखित सूचनाओं का उपयोग करते हैं -
- बिग ओ संकेतन
- ओमेगा संकेतन
- थीटा संकेतन
बिग ओ संकेतन
गणित में, बिग ओ अंकन का उपयोग कार्यों की स्पर्शोन्मुख विशेषताओं का प्रतिनिधित्व करने के लिए किया जाता है। यह एक सरल और सटीक विधि में बड़े इनपुट के लिए एक फ़ंक्शन के व्यवहार का प्रतिनिधित्व करता है। यह एक एल्गोरिथ्म के निष्पादन समय के ऊपरी हिस्से का प्रतिनिधित्व करने की एक विधि है। यह उस समय की सबसे लंबी मात्रा का प्रतिनिधित्व करता है जिसे एल्गोरिथ्म अपने निष्पादन को पूरा करने में ले सकता है। समारोह -
f (n) = O (g (n))
अगर वहाँ सकारात्मक स्थिरांक मौजूद है c तथा n0 ऐसा है कि f(n) ≤ c * g(n) सबके लिए n कहाँ पे n ≥ n0।
ओमेगा संकेतन
ओमेगा संकेतन एक एल्गोरिथ्म के निष्पादन समय के निचले हिस्से का प्रतिनिधित्व करने की एक विधि है। समारोह -
f (n) = Ω (g (n))
अगर वहाँ सकारात्मक स्थिरांक मौजूद है c तथा n0 ऐसा है कि f(n) ≥ c * g(n) सबके लिए n कहाँ पे n ≥ n0।
थीटा संकेतन
थीटा संकेतन एक एल्गोरिथम के निष्पादन समय के निचले बाउंड और ऊपरी बाउंड दोनों का प्रतिनिधित्व करने की एक विधि है। समारोह -
f (n) = θ (g (n))
अगर वहाँ सकारात्मक स्थिरांक मौजूद है c1, c2, तथा n0 ऐसे कि c1 * g (n) c f (n) * c2 * g (n) सभी के लिए n कहाँ पे n ≥ n0।
एक एल्गोरिथ्म का स्पीडअप
एक समानांतर एल्गोरिदम का प्रदर्शन इसकी गणना करके निर्धारित किया जाता है speedup। स्पीडअप को समानांतर एल्गोरिथम के सबसे खराब-निष्पादन निष्पादन समय के लिए किसी विशेष समस्या के लिए सबसे तेजी से ज्ञात अनुक्रमिक एल्गोरिदम के सबसे खराब-निष्पादन निष्पादन समय के अनुपात के रूप में परिभाषित किया गया है।
प्रयुक्त प्रोसेसर की संख्या
उपयोग किए जाने वाले प्रोसेसर की संख्या समानांतर एल्गोरिथम की दक्षता का विश्लेषण करने के लिए एक महत्वपूर्ण कारक है। कंप्यूटर खरीदने, बनाए रखने और चलाने की लागत की गणना की जाती है। किसी समस्या को हल करने के लिए एल्गोरिथ्म द्वारा उपयोग किए जाने वाले प्रोसेसर की संख्या से अधिक, अधिक महंगा परिणाम प्राप्त होता है।
कुल लागत
समानांतर एल्गोरिथम की कुल लागत समय की जटिलता और उस विशेष एल्गोरिथ्म में उपयोग किए जाने वाले प्रोसेसर की संख्या है।
कुल लागत = समय जटिलता × प्रयुक्त प्रोसेसर की संख्या
इसलिए efficiency एक समानांतर एल्गोरिथ्म का है -
डेटा और प्रोसेसिंग विधि को विभाजित करने और इंटरैक्शन को कम करने के लिए उपयुक्त रणनीति लागू करने के लिए एक रणनीति पर विचार करके एक समानांतर एल्गोरिदम का मॉडल विकसित किया गया है। इस अध्याय में, हम निम्नलिखित समानांतर एल्गोरिदम मॉडल पर चर्चा करेंगे -
- डेटा समानांतर मॉडल
- टास्क ग्राफ मॉडल
- काम पूल मॉडल
- मास्टर गुलाम मॉडल
- निर्माता उपभोक्ता या पाइपलाइन मॉडल
- हाइब्रिड मॉडल
डेटा समानांतर
डेटा समानांतर मॉडल में, कार्यों को प्रक्रियाओं को सौंपा गया है और प्रत्येक कार्य विभिन्न डेटा पर समान प्रकार के संचालन करता है। Data parallelism एकल संचालन का एक परिणाम है जो कई डेटा आइटम पर लागू किया जा रहा है।
डेटा-समानांतर मॉडल को साझा-पता स्थान और संदेश-पासिंग प्रतिमानों पर लागू किया जा सकता है। डेटा-समानांतर मॉडल में, बातचीत के ओवरहेड्स को एक स्थानीयता विघटन विघटन का चयन करके, अनुकूलित सामूहिक बातचीत दिनचर्या का उपयोग करके, या कम्प्यूटेशन और इंटरैक्शन को ओवरलैप करके कम किया जा सकता है।
डेटा-समानांतर मॉडल समस्याओं की प्राथमिक विशेषता यह है कि समस्या के आकार के साथ डेटा समानांतरवाद की तीव्रता बढ़ जाती है, जो बदले में बड़ी समस्याओं को हल करने के लिए अधिक प्रक्रियाओं का उपयोग करना संभव बनाता है।
Example - घना मैट्रिक्स गुणन।

टास्क ग्राफ मॉडल
टास्क ग्राफ मॉडल में, समानता एक द्वारा व्यक्त की जाती है task graph। एक कार्य ग्राफ या तो तुच्छ या अनैतिक हो सकता है। इस मॉडल में, स्थानीय लोगों को बढ़ावा देने या बातचीत की लागत को कम करने के लिए कार्यों के बीच संबंध का उपयोग किया जाता है। इस मॉडल को उन समस्याओं को हल करने के लिए लागू किया जाता है जिसमें कार्यों से जुड़े डेटा की मात्रा उनके साथ जुड़े गणना की संख्या की तुलना में बहुत बड़ी है। कार्यों के बीच डेटा आंदोलन की लागत में सुधार करने में मदद करने के लिए कार्यों को सौंपा गया है।
Examples - समानांतर त्वरित सॉर्ट, विरल मैट्रिक्स फैक्टराइजेशन, और डिवाइड-एंड-कॉनकेयर दृष्टिकोण के माध्यम से समानांतर समानांतर एल्गोरिदम।
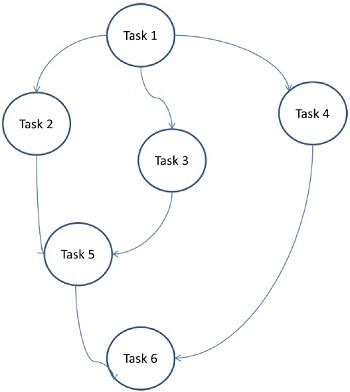
यहां, समस्याओं को परमाणु कार्यों में विभाजित किया गया है और एक ग्राफ के रूप में लागू किया गया है। प्रत्येक कार्य नौकरी की एक स्वतंत्र इकाई है जिसमें एक या एक से अधिक कार्य पर निर्भरता होती है। किसी कार्य के पूरा होने के बाद, एक पूर्ववर्ती कार्य का आउटपुट निर्भर कार्य को पारित किया जाता है। एंटीकेडेंट टास्क वाला एक टास्क तभी शुरू होता है जब उसका पूरा एंटेकेड टास्क पूरा हो जाता है। अंतिम निर्भर कार्य पूरा होने पर ग्राफ का अंतिम आउटपुट प्राप्त होता है (उपरोक्त आकृति में टास्क 6)।
काम पूल मॉडल
कार्य पूल मॉडल में, कार्यों को लोड को संतुलित करने के लिए प्रक्रियाओं को गतिशील रूप से सौंपा गया है। इसलिए, कोई भी प्रक्रिया संभावित रूप से किसी भी कार्य को अंजाम दे सकती है। इस मॉडल का उपयोग तब किया जाता है जब कार्यों से जुड़े डेटा की मात्रा, कार्यों से जुड़े गणना की तुलना में तुलनात्मक रूप से छोटी हो।
प्रक्रियाओं पर कार्यों का कोई वांछित पूर्व असाइनमेंट नहीं है। कार्यों का निरूपण केंद्रीकृत या विकेन्द्रीकृत है। कार्यों के संकेत एक भौतिक रूप से साझा सूची में, एक प्राथमिकता कतार में, या हैश टेबल या पेड़ में सहेजे जाते हैं, या उन्हें भौतिक रूप से वितरित डेटा संरचना में सहेजा जा सकता है।
कार्य शुरुआत में उपलब्ध हो सकता है, या गतिशील रूप से उत्पन्न हो सकता है। यदि कार्य गतिशील रूप से उत्पन्न होता है और कार्य का विकेंद्रीकृत असाइनमेंट किया जाता है, तो एक समाप्ति का पता लगाने के एल्गोरिथ्म की आवश्यकता होती है ताकि सभी प्रक्रियाएं वास्तव में पूरे कार्यक्रम के पूरा होने का पता लगा सकें और अधिक कार्यों की तलाश करना बंद कर सकें।
Example - समानांतर पेड़ खोज

मास्टर-स्लेव मॉडल
मास्टर-स्लेव मॉडल में, एक या अधिक मास्टर प्रक्रियाएं कार्य उत्पन्न करती हैं और इसे दास प्रक्रियाओं के लिए आवंटित करती हैं। कार्य पहले से आवंटित हो सकते हैं यदि -
- मास्टर कार्यों की मात्रा का अनुमान लगा सकता है, या
- एक यादृच्छिक असाइनमेंट लोड को संतुलित करने का एक संतोषजनक काम कर सकता है, या
- दासों को अलग-अलग समय में कार्य के छोटे टुकड़े सौंपे जाते हैं।
यह मॉडल आमतौर पर समान रूप से उपयुक्त है shared-address-space या message-passing paradigms, चूंकि बातचीत स्वाभाविक रूप से दो तरह से होती है।
कुछ मामलों में, एक कार्य को चरणों में पूरा करने की आवश्यकता हो सकती है, और अगले चरण में कार्य उत्पन्न होने से पहले प्रत्येक चरण में कार्य पूरा होना चाहिए। मास्टर-स्लेव मॉडल को सामान्यीकृत किया जा सकता हैhierarchical या multi-level master-slave model जिसमें शीर्ष स्तर का मास्टर कार्यों के बड़े हिस्से को दूसरे स्तर के मास्टर को खिलाता है, जो अपने स्वयं के दासों के बीच कार्यों को आगे बढ़ाता है और कार्य का एक हिस्सा खुद कर सकता है।
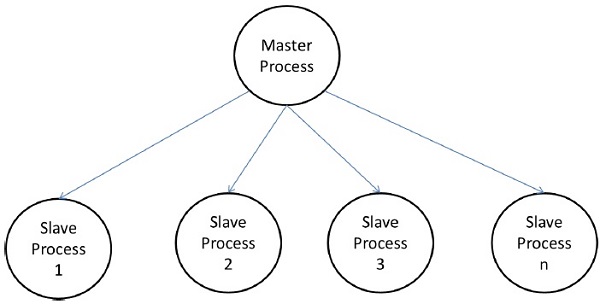
मास्टर-दास मॉडल का उपयोग करने में सावधानी
यह सुनिश्चित करने के लिए ध्यान रखा जाना चाहिए कि मास्टर एक भीड़ बिंदु न बन जाए। यदि कार्य बहुत छोटे हैं या श्रमिक तुलनात्मक रूप से तेज़ हैं तो ऐसा हो सकता है।
कार्यों को इस तरह से चुना जाना चाहिए कि कार्य करने की लागत संचार की लागत और सिंक्रनाइज़ेशन की लागत पर हावी हो।
एसिंक्रोनस इंटरैक्शन मास्टर द्वारा ओवरलैप इंटरैक्शन और वर्क जेनरेशन से जुड़ी गणना में मदद कर सकता है।
पाइपलाइन मॉडल
इसे के रूप में भी जाना जाता है producer-consumer model। यहां डेटा की एक सेट को प्रक्रियाओं की एक श्रृंखला के माध्यम से पारित किया जाता है, जिनमें से प्रत्येक उस पर कुछ कार्य करता है। यहां, नए डेटा का आगमन कतार में एक प्रक्रिया द्वारा एक नए कार्य के निष्पादन को उत्पन्न करता है। प्रक्रियाएं रैखिक या बहुआयामी सरणियों, पेड़ों या चक्रों के साथ या बिना सामान्य रेखांकन के आकार में एक कतार बना सकती हैं।
यह मॉडल उत्पादकों और उपभोक्ताओं की एक श्रृंखला है। कतार में प्रत्येक प्रक्रिया को कतार में पूर्ववर्ती प्रक्रिया के लिए डेटा आइटम के अनुक्रम के उपभोक्ता के रूप में माना जा सकता है और कतार में इसके बाद की प्रक्रिया के लिए डेटा के एक निर्माता के रूप में। कतार को एक रैखिक श्रृंखला होने की आवश्यकता नहीं है; यह एक निर्देशित ग्राफ हो सकता है। इस मॉडल पर लागू होने वाली सबसे सामान्य इंटरैक्शन मिनिमाइजेशन तकनीक कम्प्यूटेशन के साथ इंटरैक्शन को ओवरलैप कर रही है।
Example - समानांतर एलयू फैक्टराइजेशन एल्गोरिदम।

हाइब्रिड मॉडल
हाइब्रिड एल्गोरिथम मॉडल की आवश्यकता तब होती है जब किसी समस्या को हल करने के लिए एक से अधिक मॉडल की आवश्यकता हो सकती है।
एक हाइब्रिड मॉडल या तो कई मॉडलों से बना हो सकता है जो पदानुक्रमित रूप से लागू किए गए हों या एक समानांतर एल्गोरिथम के विभिन्न चरणों में कई मॉडल क्रमिक रूप से लागू होते हैं।
Example - समानांतर त्वरित प्रकार
Parallel Random Access Machines (PRAM)एक मॉडल है, जिसे अधिकांश समानांतर एल्गोरिदम के लिए माना जाता है। यहां, कई प्रोसेसर मेमोरी के सिंगल ब्लॉक से जुड़े होते हैं। एक PRAM मॉडल में शामिल हैं -
इसी प्रकार के प्रोसेसर का एक सेट।
सभी प्रोसेसर एक सामान्य मेमोरी यूनिट साझा करते हैं। प्रोसेसर केवल साझा मेमोरी के माध्यम से आपस में संवाद कर सकते हैं।
एक मेमोरी एक्सेस यूनिट (MAU) प्रोसेसर को एकल साझा मेमोरी के साथ जोड़ती है।

यहाँ, n प्रोसेसर की संख्या पर स्वतंत्र संचालन कर सकते हैं nसमय की एक विशेष इकाई में डेटा की संख्या। इसके परिणामस्वरूप विभिन्न प्रोसेसरों द्वारा एक ही मेमोरी लोकेशन को एक साथ एक्सेस किया जा सकता है।
इस समस्या को हल करने के लिए, PRAM मॉडल पर निम्नलिखित बाधाओं को लागू किया गया है -
Exclusive Read Exclusive Write (EREW) - यहां किसी भी दो प्रोसेसर को एक ही समय में एक ही मेमोरी लोकेशन से पढ़ने या लिखने की अनुमति नहीं है।
Exclusive Read Concurrent Write (ERCW) - यहां किसी भी दो प्रोसेसर को एक ही मेमोरी स्थान से एक ही समय में पढ़ने की अनुमति नहीं है, लेकिन एक ही समय में एक ही मेमोरी स्थान पर लिखने की अनुमति है।
Concurrent Read Exclusive Write (CREW) - यहाँ सभी प्रोसेसरों को एक ही समय में एक ही मेमोरी लोकेशन से पढ़ने की अनुमति है, लेकिन एक ही समय में एक ही मेमोरी लोकेशन पर लिखने की अनुमति नहीं है।
Concurrent Read Concurrent Write (CRCW) - सभी प्रोसेसर को एक ही समय में एक ही मेमोरी स्थान से पढ़ने या लिखने की अनुमति है।
PRAM मॉडल को लागू करने के कई तरीके हैं, लेकिन सबसे प्रमुख हैं -
- साझा स्मृति मॉडल
- संदेश पासिंग मॉडल
- डेटा समानांतर मॉडल
साझा स्मृति मॉडल
साझा मेमोरी पर जोर दिया गया है control parallelism की तुलना में data parallelism। साझा किए गए मेमोरी मॉडल में, कई प्रोसेस अलग-अलग प्रोसेसर पर स्वतंत्र रूप से निष्पादित होते हैं, लेकिन वे एक आम मेमोरी स्पेस साझा करते हैं। किसी भी प्रोसेसर गतिविधि के कारण, यदि किसी भी मेमोरी लोकेशन में कोई परिवर्तन होता है, तो यह बाकी प्रोसेसर के लिए दिखाई देता है।
जैसा कि कई प्रोसेसर एक ही मेमोरी लोकेशन तक पहुंचते हैं, ऐसा हो सकता है कि किसी विशेष समय पर, एक से अधिक प्रोसेसर एक ही मेमोरी लोकेशन तक पहुंच रहे हों। मान लीजिए कि कोई उस स्थान को पढ़ रहा है और दूसरा उस स्थान पर लिख रहा है। यह भ्रम पैदा कर सकता है। इससे बचने के लिए, कुछ नियंत्रण तंत्र, जैसेlock / semaphore, आपसी बहिष्कार सुनिश्चित करने के लिए लागू किया गया है।

साझा मेमोरी प्रोग्रामिंग निम्नलिखित में लागू की गई है -
Thread libraries- थ्रेड लाइब्रेरी नियंत्रण के कई थ्रेड्स की अनुमति देता है जो समान मेमोरी लोकेशन में समवर्ती रूप से चलते हैं। थ्रेड लाइब्रेरी एक इंटरफ़ेस प्रदान करता है जो सबरूटीन की लाइब्रेरी के माध्यम से मल्टीथ्रेडिंग का समर्थन करता है। इसमें सबरूटीन्स होते हैं
- धागे बनाना और नष्ट करना
- धागे का समयबद्ध निष्पादन
- धागे के बीच डेटा और संदेश पारित करना
- थ्रेड संदर्भों को सहेजना और पुनर्स्थापित करना
थ्रेड पुस्तकालयों के उदाहरणों में शामिल हैं - सोलारिस के लिए सोलारिसटीएम थ्रेड्स, लिनक्स में लागू किए गए पोसिक्स थ्रेड्स, विंडोज एनटी और विंडोज 2000 में उपलब्ध विन 32 थ्रेड्स, और जावाटीएम थ्रेड्स मानक जावाटीएम डेवलपमेंट किट (जेडडीके) के हिस्से के रूप में।
Distributed Shared Memory (DSM) Systems- डीएसएम सिस्टम हार्डवेयर समर्थन के बिना साझा मेमोरी प्रोग्रामिंग को लागू करने के लिए शिथिल युग्मित वास्तुकला पर साझा स्मृति का एक अमूर्त निर्माण करते हैं। वे मानक पुस्तकालयों को लागू करते हैं और आधुनिक ऑपरेटिंग सिस्टम में मौजूद उन्नत उपयोगकर्ता-स्तरीय मेमोरी प्रबंधन सुविधाओं का उपयोग करते हैं। उदाहरणों में ट्रेड मार्क सिस्टम, मुनिन, आईवीवाई, शास्ता, ब्रेज़ोस और कश्मीरी शामिल हैं।
Program Annotation Packages- यह समान मेमोरी एक्सेस विशेषताओं वाले आर्किटेक्चर पर लागू किया गया है। प्रोग्राम एनोटेशन पैकेज का सबसे उल्लेखनीय उदाहरण OpenMP है। OpenMP क्रियात्मक समानता को लागू करता है। यह मुख्य रूप से छोरों के समानांतरकरण पर केंद्रित है।
साझा मेमोरी की अवधारणा साझा मेमोरी सिस्टम का निम्न-स्तर नियंत्रण प्रदान करती है, लेकिन यह थकाऊ और गलत है। यह एप्लिकेशन प्रोग्रामिंग की तुलना में सिस्टम प्रोग्रामिंग के लिए अधिक लागू है।
साझा मेमोरी प्रोग्रामिंग के गुण
ग्लोबल एड्रेस स्पेस मेमोरी के लिए उपयोगकर्ता के अनुकूल प्रोग्रामिंग दृष्टिकोण देता है।
सीपीयू में मेमोरी की निकटता के कारण, प्रक्रियाओं के बीच डेटा साझाकरण तेज और समान है।
प्रक्रियाओं के बीच डेटा के संचार को स्पष्ट रूप से निर्दिष्ट करने की आवश्यकता नहीं है।
प्रक्रिया-संचार ओवरहेड नगण्य है।
इसे सीखना बहुत आसान है।
साझा मेमोरी प्रोग्रामिंग के प्रदर्शन
- यह पोर्टेबल नहीं है।
- डेटा इलाके का प्रबंधन करना बहुत मुश्किल है।
संदेश पासिंग मॉडल
संदेश का वितरण वितरित मेमोरी सिस्टम में सबसे अधिक इस्तेमाल किया जाने वाला समानांतर प्रोग्रामिंग दृष्टिकोण है। यहां, प्रोग्रामर को समानता का निर्धारण करना होगा। इस मॉडल में, सभी प्रोसेसरों की अपनी स्थानीय मेमोरी यूनिट होती है और वे संचार नेटवर्क के माध्यम से डेटा का आदान-प्रदान करते हैं।

प्रोसेसर आपस में संचार के लिए संदेश-पासिंग लाइब्रेरी का उपयोग करते हैं। भेजे जा रहे डेटा के साथ, संदेश में निम्नलिखित घटक हैं -
प्रोसेसर का पता जिससे संदेश भेजा जा रहा है;
भेजने वाले प्रोसेसर में डेटा की मेमोरी लोकेशन का पता शुरू करना;
डेटा भेजने का डेटा प्रकार;
भेजने वाले डेटा का डेटा आकार;
प्रोसेसर का पता जिस पर संदेश भेजा जा रहा है;
प्राप्त करने वाले प्रोसेसर में डेटा के लिए स्मृति स्थान का पता शुरू करना।
प्रोसेसर निम्नलिखित तरीकों में से किसी भी एक दूसरे के साथ संवाद कर सकते हैं -
- पॉइंट-टू-पॉइंट कम्युनिकेशन
- सामूहिक संचार
- संदेश पासिंग इंटरफ़ेस
पॉइंट-टू-पॉइंट कम्युनिकेशन
पॉइंट-टू-पॉइंट संचार संदेश पासिंग का सबसे सरल रूप है। यहां, संदेश भेजने वाले प्रोसेसर से एक संदेश प्राप्त करने वाले प्रोसेसर को निम्नलिखित में से किसी भी स्थानांतरण मोड से भेजा जा सकता है -
Synchronous mode - अगला संदेश केवल एक पुष्टिकरण प्राप्त करने के बाद भेजा जाता है कि संदेश के अनुक्रम को बनाए रखने के लिए, इसका पिछला संदेश दिया गया है।
Asynchronous mode - अगला संदेश भेजने के लिए, पिछले संदेश की डिलीवरी की पुष्टि की आवश्यकता नहीं है।
सामूहिक संचार
सामूहिक संचार में संदेश पारित करने के लिए दो से अधिक प्रोसेसर शामिल हैं। निम्नलिखित मोड सामूहिक संचार की अनुमति देते हैं -
Barrier - बैरियर मोड संभव है अगर संचार में शामिल सभी प्रोसेसर एक विशेष बॉक (जिसे ज्ञात है) चलाते हैं barrier block) संदेश पारित करने के लिए।
Broadcast - प्रसारण दो प्रकार का होता है -
One-to-all - यहाँ, एक सिंगल ऑपरेशन वाला एक प्रोसेसर अन्य सभी प्रोसेसर को एक ही संदेश भेजता है।
All-to-all - यहां, सभी प्रोसेसर अन्य सभी प्रोसेसर को संदेश भेजते हैं।
प्रसारित संदेश तीन प्रकार के हो सकते हैं -
Personalized - अन्य सभी डेस्टिनेशन प्रोसिजर्स को यूनीक मैसेज भेजे जाते हैं।
Non-personalized - सभी गंतव्य प्रोसेसर एक ही संदेश प्राप्त करते हैं।
Reduction - प्रसारण को कम करने में, समूह का एक प्रोसेसर समूह के अन्य सभी प्रोसेसर से सभी संदेशों को इकट्ठा करता है और उन्हें एक एकल संदेश के साथ संयोजित करता है, जिसे समूह के अन्य सभी प्रोसेसर एक्सेस कर सकते हैं।
संदेश पास करने का गुण
- समानता के निम्न-स्तरीय नियंत्रण प्रदान करता है;
- यह पोर्टेबल है;
- कम त्रुटि वाले प्रवण;
- समानांतर सिंक्रनाइज़ेशन और डेटा वितरण में कम ओवरहेड।
संदेश पासिंग के लाभ
समानांतर साझा-मेमोरी कोड की तुलना में, संदेश-पासिंग कोड को आमतौर पर अधिक सॉफ्टवेयर ओवरहेड की आवश्यकता होती है।
संदेश पासिंग लाइब्रेरी
कई संदेश-गुजरने वाले पुस्तकालय हैं। यहाँ, हम दो सबसे ज्यादा इस्तेमाल होने वाले संदेश-पुस्तकालयों पर चर्चा करेंगे -
- संदेश पासिंग इंटरफ़ेस (MPI)
- समानांतर वर्चुअल मशीन (PVM)
संदेश पासिंग इंटरफ़ेस (MPI)
यह वितरित मेमोरी सिस्टम में सभी समवर्ती प्रक्रियाओं के बीच संचार प्रदान करने के लिए एक सार्वभौमिक मानक है। आमतौर पर उपयोग किए जाने वाले समानांतर कंप्यूटिंग प्लेटफार्मों में से अधिकांश संदेश पासिंग इंटरफ़ेस का कम से कम एक कार्यान्वयन प्रदान करते हैं। इसे पूर्वनिर्धारित कार्यों के संग्रह के रूप में लागू किया गया हैlibrary और C, C ++, फोरट्रान, इत्यादि भाषाओं से कॉल किया जा सकता है। MPIs अन्य संदेश पासिंग लाइब्रेरी की तुलना में तेज और पोर्टेबल हैं।
Merits of Message Passing Interface
केवल साझा मेमोरी आर्किटेक्चर या वितरित मेमोरी आर्किटेक्चर पर चलता है;
प्रत्येक प्रोसेसर के अपने स्थानीय चर होते हैं;
बड़े साझा मेमोरी कंप्यूटर की तुलना में, वितरित मेमोरी कंप्यूटर कम महंगे हैं।
Demerits of Message Passing Interface
- समानांतर एल्गोरिथ्म के लिए अधिक प्रोग्रामिंग परिवर्तन आवश्यक हैं;
- कभी-कभी डिबग करना मुश्किल होता है; तथा
- नोड्स के बीच संचार नेटवर्क में अच्छा प्रदर्शन नहीं करता है।
समानांतर वर्चुअल मशीन (PVM)
PVM एक पोर्टेबल मैसेज पासिंग सिस्टम है, जो एक ही वर्चुअल मशीन बनाने के लिए अलग-अलग विषम होस्ट मशीनों को जोड़ने के लिए डिज़ाइन किया गया है। यह एकल प्रबंधनीय समानांतर कंप्यूटिंग संसाधन है। सुपरकंडक्टिविटी अध्ययन, आणविक गतिशीलता सिमुलेशन और मैट्रिक्स एल्गोरिदम जैसी बड़ी कम्प्यूटेशनल समस्याओं को कई कंप्यूटरों की मेमोरी और कुल शक्ति का उपयोग करके अधिक लागत को प्रभावी ढंग से हल किया जा सकता है। यह असंगत कंप्यूटर आर्किटेक्चर के नेटवर्क में सभी संदेश रूटिंग, डेटा रूपांतरण, कार्य शेड्यूलिंग का प्रबंधन करता है।
Features of PVM
- स्थापित करने और कॉन्फ़िगर करने में बहुत आसान;
- एकाधिक उपयोगकर्ता एक ही समय में पीवीएम का उपयोग कर सकते हैं;
- एक उपयोगकर्ता कई अनुप्रयोगों को निष्पादित कर सकता है;
- यह एक छोटा पैकेज है;
- सी, सी ++, फोरट्रान का समर्थन करता है;
- पीवीएम प्रोग्राम के दिए गए रन के लिए, उपयोगकर्ता मशीनों के समूह का चयन कर सकते हैं;
- यह एक संदेश भेजने वाला मॉडल है,
- प्रक्रिया-आधारित संगणना;
- विषम वास्तुकला का समर्थन करता है।
डेटा समानांतर प्रोग्रामिंग
डेटा समानांतर प्रोग्रामिंग मॉडल का प्रमुख ध्यान एक साथ सेट किए गए डेटा पर संचालन करने पर है। डेटा सेट को किसी संरचना जैसे कि एक सरणी, हाइपरक्यूब आदि में व्यवस्थित किया जाता है। प्रोसेसर समान डेटा संरचना पर सामूहिक रूप से संचालन करते हैं। प्रत्येक कार्य एक ही डेटा संरचना के एक अलग विभाजन पर किया जाता है।
यह प्रतिबंधात्मक है, क्योंकि सभी एल्गोरिदम को डेटा समानता के संदर्भ में निर्दिष्ट नहीं किया जा सकता है। यही कारण है कि डेटा समानता सार्वभौमिक नहीं है।
डेटा समानांतर भाषाएं प्रोसेसर को डेटा अपघटन और मैपिंग को निर्दिष्ट करने में मदद करती हैं। इसमें डेटा वितरण स्टेटमेंट भी शामिल है जो प्रोग्रामर को डेटा पर नियंत्रण रखने की अनुमति देता है - उदाहरण के लिए, कौन सा डेटा किस प्रोसेसर पर जाएगा - प्रोसेसर के भीतर संचार की मात्रा को कम करने के लिए।
किसी भी एल्गोरिथ्म को ठीक से लागू करने के लिए, यह बहुत महत्वपूर्ण है कि आप एक उचित डेटा संरचना का चयन करें। ऐसा इसलिए है क्योंकि डेटा संरचना पर किया गया एक विशेष ऑपरेशन किसी अन्य डेटा संरचना पर किए गए समान ऑपरेशन की तुलना में अधिक समय ले सकता है।
Example- एक सरणी का उपयोग करके एक सेट में i वें तत्व तक पहुंचने के लिए , इसमें निरंतर समय लग सकता है लेकिन एक लिंक की गई सूची का उपयोग करके, उसी ऑपरेशन को करने के लिए आवश्यक समय एक बहुपद बन सकता है।
इसलिए, डेटा संरचना का चयन वास्तुकला और संचालन के प्रकार पर विचार करना चाहिए।
निम्नलिखित डेटा संरचनाएं आमतौर पर समानांतर प्रोग्रामिंग में उपयोग की जाती हैं -
- लिंक्ड सूची
- Arrays
- हाइपरक्यूब नेटवर्क
लिंक्ड सूची
एक लिंक की गई सूची एक डेटा संरचना है जिसमें पॉइंटर्स द्वारा शून्य या अधिक नोड्स जुड़े हुए हैं। नोड्स लगातार मेमोरी स्थानों पर कब्जा कर सकते हैं या नहीं कर सकते हैं। प्रत्येक नोड के दो या तीन भाग होते हैं - एकdata part डेटा संग्रहीत करता है और अन्य दो हैं link fieldsवह पिछले या अगले नोड का पता संग्रहीत करता है। पहला नोड का पता बाहरी पॉइंटर में संग्रहीत होता है जिसे कहा जाता हैhead। अंतिम नोड, के रूप में जाना जाता हैtail, आम तौर पर कोई पता नहीं होता है।
तीन प्रकार की लिंक्ड लिस्ट हैं -
- सिंगली लिंक्ड लिस्ट
- संदेह से जुड़ी सूची
- सर्कुलर लिंक्ड सूची
सिंगली लिंक्ड लिस्ट
एक एकल लिंक की गई सूची के नोड में डेटा और अगले नोड का पता होता है। बाहरी सूचक कहा जाता हैhead पहले नोड का पता संग्रहीत करता है।

संदेह से जुड़ी सूची
एक डबल लिंक की गई सूची के नोड में डेटा और पिछले और अगले नोड दोनों का पता होता है। बाहरी सूचक कहा जाता हैhead पहले नोड और बाहरी पॉइंटर नामक पते को संग्रहीत करता है tail अंतिम नोड का पता संग्रहीत करता है।

सर्कुलर लिंक्ड सूची
एक सर्कुलर लिंक्ड लिस्ट इस बात को छोड़कर सिंगली लिंक्ड लिस्ट से काफी मिलती-जुलती है, क्योंकि पिछले नोड ने पहले नोड के पते को बचाया था।

सरणियों
एक सरणी एक डेटा संरचना है जहां हम समान प्रकार के डेटा को संग्रहीत कर सकते हैं। यह एक आयामी या बहुआयामी हो सकता है। ऐरे को सांख्यिकीय या गतिशील रूप से बनाया जा सकता है।
में statically declared arrays, संकलन के समय सरणियों के आयाम और आकार को जाना जाता है।
में dynamically declared arrays, सरणी का आयाम और आकार रनटाइम पर जाना जाता है।
साझा मेमोरी प्रोग्रामिंग के लिए, सरणियों का उपयोग एक आम मेमोरी के रूप में किया जा सकता है और डेटा समानांतर प्रोग्रामिंग के लिए, उन्हें उप-सरणियों में विभाजित करके उपयोग किया जा सकता है।
हाइपरक्यूब नेटवर्क
हाइपरक्यूब वास्तुकला उन समानांतर एल्गोरिदम के लिए सहायक है जहां प्रत्येक कार्य को अन्य कार्यों के साथ संवाद करना पड़ता है। हाइपरक्यूब टोपोलॉजी आसानी से रिंग और मेष जैसे अन्य टोपोलॉजी को एम्बेड कर सकती है। इसे एन-क्यूब्स के रूप में भी जाना जाता है, जहांnआयामों की संख्या है। एक हाइपरक्यूब का निर्माण पुनरावर्ती रूप से किया जा सकता है।


समानांतर एल्गोरिथम के लिए एक उचित डिजाइनिंग तकनीक का चयन करना सबसे कठिन और महत्वपूर्ण कार्य है। अधिकांश समानांतर प्रोग्रामिंग समस्याओं में एक से अधिक समाधान हो सकते हैं। इस अध्याय में, हम समानांतर एल्गोरिदम के लिए निम्नलिखित डिजाइनिंग तकनीकों पर चर्चा करेंगे -
- विभाजन और जीत
- लालची विधि
- गतिशील प्रोग्रामिंग
- Backtracking
- शाखा और बाउंड
- रैखिक प्रोग्रामिंग
फूट डालो और जीतो विधि
विभाजन और जीत के दृष्टिकोण में, समस्या को कई छोटी उप-समस्याओं में विभाजित किया गया है। फिर उप-समस्याओं को मूल समस्या का समाधान प्राप्त करने के लिए पुनरावर्ती और संयुक्त रूप से हल किया जाता है।
फूट डालो और जीतो दृष्टिकोण में प्रत्येक स्तर पर निम्नलिखित चरण शामिल हैं -
Divide - मूल समस्या को उप-समस्याओं में विभाजित किया गया है।
Conquer - उप-समस्याओं को पुनरावर्ती रूप से हल किया जाता है।
Combine - मूल समस्या के समाधान के लिए उप-समस्याओं के समाधान को एक साथ जोड़ा जाता है।
फूट डालो और जीतो दृष्टिकोण निम्नलिखित एल्गोरिदम में लागू किया जाता है -
- द्विआधारी खोज
- जल्दी से सुलझाएं
- मर्ज़ सॉर्ट
- पूर्णांक गुणा
- मैट्रिक्स उलटा
- मैट्रिक्स गुणन
लालची विधि
अनुकूलन समाधान के लालची एल्गोरिथ्म में, किसी भी क्षण सबसे अच्छा समाधान चुना जाता है। जटिल समस्याओं को लागू करने के लिए एक लालची एल्गोरिथ्म बहुत आसान है। यह निर्णय करता है कि कौन सा कदम अगले चरण में सबसे सटीक समाधान प्रदान करेगा।
यह एल्गोरिथ्म एक कहा जाता है greedyक्योंकि जब छोटे उदाहरण के लिए इष्टतम समाधान प्रदान किया जाता है, तो एल्गोरिथ्म कुल प्रोग्राम को संपूर्ण नहीं मानता है। एक बार जब एक समाधान पर विचार किया जाता है, तो लालची एल्गोरिथ्म फिर से उसी समाधान पर विचार नहीं करता है।
एक लालची एल्गोरिथ्म पुनरावर्ती रूप से सबसे छोटे संभव घटक भागों से वस्तुओं का एक समूह बनाने का काम करता है। रिकर्सन एक समस्या को हल करने की एक प्रक्रिया है जिसमें किसी विशेष समस्या का समाधान उस समस्या के छोटे उदाहरण के समाधान पर निर्भर होता है।
गतिशील प्रोग्रामिंग
डायनेमिक प्रोग्रामिंग एक ऑप्टिमाइज़ेशन तकनीक है, जो समस्या को छोटी उप-समस्याओं में विभाजित करती है और प्रत्येक उप-समस्या को हल करने के बाद, डायनेमिक प्रोग्रामिंग अंतिम समाधान प्राप्त करने के लिए सभी समाधानों को जोड़ती है। विभाजन और जीत की विधि के विपरीत, गतिशील प्रोग्रामिंग कई बार उप-समस्याओं के समाधान का पुन: उपयोग करता है।
फाइबोनैचि श्रृंखला के लिए पुनरावर्ती एल्गोरिथ्म गतिशील प्रोग्रामिंग का एक उदाहरण है।
एल्गोरिदम को पीछे कर रहा है
कॉम्बिनेशन संबंधी समस्याओं को हल करने के लिए बैकट्रैकिंग एक अनुकूलन तकनीक है। यह प्रोग्रामेटिक और रियल-लाइफ दोनों समस्याओं पर लागू होता है। आठ रानी समस्या, सुडोकू पहेली और भूलभुलैया से गुजरना ऐसे लोकप्रिय उदाहरण हैं जहां बैकग्राउंडिंग एल्गोरिदम का उपयोग किया जाता है।
बैकट्रैकिंग में, हम एक संभावित समाधान के साथ शुरू करते हैं, जो सभी आवश्यक शर्तों को पूरा करता है। फिर हम अगले स्तर पर चले जाते हैं और यदि वह स्तर संतोषजनक समाधान नहीं देता है, तो हम एक स्तर पर वापस आते हैं और एक नए विकल्प के साथ शुरू करते हैं।
शाखा और बंधन
एक शाखा और बाध्य एल्गोरिथ्म समस्या का इष्टतम समाधान प्राप्त करने के लिए एक अनुकूलन तकनीक है। यह समाधान के पूरे स्थान में किसी समस्या के लिए सबसे अच्छा समाधान ढूंढता है। अनुकूलित किए जाने वाले फ़ंक्शन में सीमाएं नवीनतम सर्वश्रेष्ठ समाधान के मूल्य के साथ विलय की जाती हैं। यह एल्गोरिथ्म को समाधान स्थान के हिस्सों को पूरी तरह से खोजने की अनुमति देता है।
एक शाखा और बाध्य खोज का उद्देश्य लक्ष्य के लिए सबसे कम लागत वाले मार्ग को बनाए रखना है। एक बार एक समाधान मिल गया है, यह समाधान में सुधार रख सकते हैं। शाखा और बाउंड सर्च को गहराई से बँधी हुई खोज और गहराई-पहली खोज में लागू किया जाता है।
रैखिक प्रोग्रामिंग
रैखिक प्रोग्रामिंग में ऑप्टिमाइज़ेशन जॉब की एक विस्तृत श्रेणी का वर्णन किया गया है जहाँ ऑप्टिमाइज़ेशन मानदंड और अवरोध दोनों रैखिक कार्य हैं। यह अधिकतम लाभ, सबसे छोटा रास्ता, या सबसे कम लागत जैसे सर्वोत्तम परिणाम प्राप्त करने की तकनीक है।
इस प्रोग्रामिंग में, हमारे पास चर का एक सेट है और हमें रैखिक समीकरणों के एक सेट को पूरा करने के लिए और दिए गए रैखिक उद्देश्य फ़ंक्शन को अधिकतम या कम करने के लिए उन्हें पूर्ण मान असाइन करना है।
एक मैट्रिक्स संख्यात्मक और गैर-संख्यात्मक डेटा का एक सेट है जिसे एक निश्चित संख्या में पंक्तियों और स्तंभों में व्यवस्थित किया जाता है। मैट्रिक्स गुणन समानांतर गणना में एक महत्वपूर्ण गुणन डिजाइन है। यहां, हम मेष और हाइपरक्यूब जैसे विभिन्न संचार नेटवर्क पर मैट्रिक्स गुणा के कार्यान्वयन पर चर्चा करेंगे। मेष और हाइपरक्यूब में उच्च नेटवर्क कनेक्टिविटी है, इसलिए वे रिंग नेटवर्क जैसे अन्य नेटवर्क की तुलना में तेज एल्गोरिदम की अनुमति देते हैं।
मैश नेटवर्क
एक टोपोलॉजी जहां नोड्स का एक सेट एक पी-आयामी ग्रिड बनाता है, एक जाल टोपोलॉजी कहा जाता है। यहां, सभी किनारे ग्रिड अक्ष के समानांतर हैं और सभी आसन्न नोड्स आपस में संवाद कर सकते हैं।
नोड्स की कुल संख्या = (पंक्ति में नोड्स की संख्या) × (कॉलम में नोड्स की संख्या)
एक जाल नेटवर्क का मूल्यांकन निम्नलिखित कारकों का उपयोग करके किया जा सकता है -
- Diameter
- बिसात की चौड़ाई
Diameter - एक जाल नेटवर्क में, सबसे लंबे समय तक distanceदो नोड्स के बीच इसका व्यास है। एक पी-आयामी जाल नेटवर्क वालेkP नोड्स का व्यास होता है p(k–1)।
Bisection width - बिज़नेस चौड़ाई एक नेटवर्क से जाल नेटवर्क को दो हिस्सों में विभाजित करने के लिए आवश्यक किनारों की न्यूनतम संख्या है।
मैट्रिक्स नेटवर्क का उपयोग मैट्रिक्स गुणन
हमने रैपराउंड कनेक्शन वाले 2D जाल नेटवर्क SIMD मॉडल पर विचार किया है। हम एक विशेष समय में n 2 प्रोसेसर का उपयोग करते हुए दो n × n सरणियों को गुणा करने के लिए एक एल्गोरिथ्म डिजाइन करेंगे ।
मैट्रिस ए और बी में क्रमशः एक आईजे और बी आईजे तत्व होते हैं। प्रसंस्करण तत्व पीई आईजे एक आईजे और बी आईजे का प्रतिनिधित्व करता है । मैट्रिक्स ए और बी को इस तरह व्यवस्थित करें कि हर प्रोसेसर में तत्वों की एक जोड़ी हो। मैट्रिक्स ए के तत्व बाईं दिशा में जाएंगे और मैट्रिक्स बी के तत्व ऊपर की दिशा में आगे बढ़ेंगे। मैट्रिक्स ए और बी में तत्वों की स्थिति में ये परिवर्तन प्रत्येक प्रसंस्करण तत्व, पीई, मूल्यों की एक नई जोड़ी को गुणा करने के लिए प्रस्तुत करते हैं।
एल्गोरिदम में कदम
- डगमगाते हुए दो मैट्रेस।
- सभी उत्पादों की गणना करें, एक ik × b kj
- चरण 2 पूरा होने पर रकम की गणना करें।
कलन विधि
Procedure MatrixMulti
Begin
for k = 1 to n-1
for all Pij; where i and j ranges from 1 to n
ifi is greater than k then
rotate a in left direction
end if
if j is greater than k then
rotate b in the upward direction
end if
for all Pij ; where i and j lies between 1 and n
compute the product of a and b and store it in c
for k= 1 to n-1 step 1
for all Pi;j where i and j ranges from 1 to n
rotate a in left direction
rotate b in the upward direction
c=c+aXb
Endहाइपरक्यूब नेटवर्क
एक हाइपरक्यूब एक एन-डायमेंशनल कंस्ट्रक्शन है, जहां किनारे आपस में लंबवत होते हैं और समान लंबाई के होते हैं। एन-आयामी हाइपरक्यूब को एन-क्यूब या एन-आयामी क्यूब के रूप में भी जाना जाता है।
2 k नोड के साथ हाइपरक्यूब की विशेषताएं
- व्यास = के
- बिसनेस चौड़ाई = 2 k-1
- किनारों की संख्या = k
हाइपरक्यूब नेटवर्क का उपयोग करके मैट्रिक्स गुणा
हाइपरक्यूब नेटवर्क के सामान्य विनिर्देश -
लश्कर N = 2mप्रोसेसर की कुल संख्या। प्रोसेसर P 0, P 1 … ..P N-1 होने दें ।
मैं और मैं चलो ख दो पूर्णांकों, 0 <i, मैं हो ख <N-1 और उसके द्विआधारी प्रतिनिधित्व केवल स्थिति ख, 0 <b <k-1 में मतभेद है।
आइए हम दो n × n मेट्रिसेस, मैट्रिक्स ए और मैट्रिक्स बी पर विचार करें।
Step 1- मैट्रिक्स ए और मैट्रिक्स बी के तत्वों को एन 3 प्रोसेसर को सौंपा गया है जैसे कि स्थिति में प्रोसेसर i, j, k में एक ji और b ik होगा ।
Step 2 - स्थिति में सभी प्रोसेसर (i, j, k) उत्पाद की गणना करता है
C (i, j, k) = A (i, j, k) × B (i, j, k)
Step 3 - 0 ≤ i where n-1, जहाँ 0, j, k <n-1 के लिए C (0, j, k) = iC (i, j, k) का योग।
ब्लॉक मैट्रिक्स
ब्लॉक मैट्रिक्स या विभाजित मैट्रिक्स एक मैट्रिक्स है जहां प्रत्येक तत्व स्वयं एक व्यक्तिगत मैट्रिक्स का प्रतिनिधित्व करता है। इन व्यक्तिगत वर्गों को एक के रूप में जाना जाता हैblock या sub-matrix।
उदाहरण


चित्रा (ए) में, एक्स एक ब्लॉक मैट्रिक्स है जहां ए, बी, सी, डी स्वयं मैट्रिक्स हैं। चित्रा (एफ) कुल मैट्रिक्स को दर्शाता है।
ब्लॉक मैट्रिक्स गुणा
जब दो ब्लॉक मेट्रिक्स स्क्वायर मैट्रिस होते हैं, तो उन्हें उसी तरह से गुणा किया जाता है जिस तरह से हम सरल मैट्रिक्स गुणा करते हैं। उदाहरण के लिए,

सॉर्टिंग एक विशेष क्रम में एक समूह में तत्वों को व्यवस्थित करने की एक प्रक्रिया है, अर्थात, आरोही क्रम, अवरोही क्रम, वर्णमाला क्रम, आदि। यहां हम निम्नलिखित पर चर्चा करेंगे -
- गणन क्रमबद्ध करें
- ऑड-इवन ट्रांसपोज़िशन सॉर्ट
- समानांतर मर्ज सॉर्ट
- हाइपर क्विक सॉर्ट
तत्वों की सूची को क्रमबद्ध करना एक बहुत ही सामान्य ऑपरेशन है। अनुक्रमिक सॉर्टिंग एल्गोरिथ्म पर्याप्त कुशल नहीं हो सकता है जब हमें डेटा की एक बड़ी मात्रा को सॉर्ट करना होगा। इसलिए, समानांतर एल्गोरिदम का उपयोग छँटाई में किया जाता है।
गणन क्रमबद्ध करें
गणना प्रकार एक सूची में सभी तत्वों की अंतिम स्थिति का पता लगाकर सूची में सभी तत्वों को व्यवस्थित करने की एक विधि है। यह प्रत्येक तत्व को अन्य सभी तत्वों के साथ तुलना करके और छोटे मूल्य वाले तत्वों की संख्या का पता लगाने के द्वारा किया जाता है।
इसलिए, किसी भी दो तत्वों के लिए, i और j में से किसी एक को निम्नलिखित में से कोई एक सत्य होना चाहिए -
- एक मैं एक < j
- ए i > ए जे
- a i = a j
कलन विधि
procedure ENUM_SORTING (n)
begin
for each process P1,j do
C[j] := 0;
for each process Pi, j do
if (A[i] < A[j]) or A[i] = A[j] and i < j) then
C[j] := 1;
else
C[j] := 0;
for each process P1, j do
A[C[j]] := A[j];
end ENUM_SORTINGऑड-इवन ट्रांसपोज़िशन सॉर्ट
Odd-Even Transposition Sort, Bubble Sort तकनीक पर आधारित है। यह दो आसन्न संख्याओं की तुलना करता है और उन्हें स्विच करता है, यदि पहला नंबर आरोही क्रम सूची प्राप्त करने के लिए दूसरी संख्या से अधिक है। विपरीत क्रम एक अवरोही क्रम श्रृंखला के लिए लागू होता है। ऑड-इवन ट्रांसपोज़िशन सॉर्ट दो चरणों में संचालित होता है -odd phase तथा even phase। दोनों चरणों में, सही में उनके आसन्न संख्या के साथ संख्याओं का आदान-प्रदान करता है।

कलन विधि
procedure ODD-EVEN_PAR (n)
begin
id := process's label
for i := 1 to n do
begin
if i is odd and id is odd then
compare-exchange_min(id + 1);
else
compare-exchange_max(id - 1);
if i is even and id is even then
compare-exchange_min(id + 1);
else
compare-exchange_max(id - 1);
end for
end ODD-EVEN_PARसमानांतर मर्ज सॉर्ट
मर्ज सॉर्ट पहले अनसोल्ड लिस्ट को सबसे छोटी संभव उप-सूचियों में विभाजित करता है, इसे आसन्न सूची के साथ तुलना करता है, और इसे सॉर्ट किए गए क्रम में मर्ज करता है। यह विभाजन को बहुत अच्छी तरह से विभाजित करके और एल्गोरिथ्म का पालन करके समानता को लागू करता है।

कलन विधि
procedureparallelmergesort(id, n, data, newdata)
begin
data = sequentialmergesort(data)
for dim = 1 to n
data = parallelmerge(id, dim, data)
endfor
newdata = data
endहाइपर क्विक सॉर्ट
हाइपर क्विक सॉर्ट हाइपरक्यूब पर त्वरित सॉर्ट का कार्यान्वयन है। इसके चरण इस प्रकार हैं -
- प्रत्येक नोड के बीच अनसुलझी सूची को विभाजित करें।
- प्रत्येक नोड को स्थानीय रूप से सॉर्ट करें।
- नोड 0 से, माध्य मान को प्रसारित करें।
- प्रत्येक सूची को स्थानीय रूप से विभाजित करें, फिर सबसे अधिक आयाम में हिस्सों का आदान-प्रदान करें।
- आयाम 0 तक पहुंचने तक समानांतर में चरण 3 और 4 को दोहराएं।
कलन विधि
procedure HYPERQUICKSORT (B, n)
begin
id := process’s label;
for i := 1 to d do
begin
x := pivot;
partition B into B1 and B2 such that B1 ≤ x < B2;
if ith bit is 0 then
begin
send B2 to the process along the ith communication link;
C := subsequence received along the ith communication link;
B := B1 U C;
endif
else
send B1 to the process along the ith communication link;
C := subsequence received along the ith communication link;
B := B2 U C;
end else
end for
sort B using sequential quicksort;
end HYPERQUICKSORTखोज कंप्यूटर विज्ञान के मूलभूत कार्यों में से एक है। इसका उपयोग उन सभी अनुप्रयोगों में किया जाता है जहां हमें यह पता लगाने की आवश्यकता होती है कि कोई तत्व दी गई सूची में है या नहीं। इस अध्याय में, हम निम्नलिखित खोज एल्गोरिदम पर चर्चा करेंगे -
- विभाजन और जीत
- गहराई-पहली खोज
- पहले चौड़ाई खोजो
- बेस्ट-फर्स्ट सर्च
विभाजन और जीत
विभाजित और जीत के दृष्टिकोण में, समस्या को कई छोटी उप-समस्याओं में विभाजित किया गया है। फिर उप-समस्याओं को मूल समस्या का समाधान प्राप्त करने के लिए पुनरावर्ती और संयुक्त रूप से हल किया जाता है।
फूट डालो और जीतो दृष्टिकोण में प्रत्येक स्तर पर निम्नलिखित चरण शामिल हैं -
Divide - मूल समस्या को उप-समस्याओं में विभाजित किया गया है।
Conquer - उप-समस्याओं को पुनरावर्ती रूप से हल किया जाता है।
Combine - मूल समस्याओं के समाधान के लिए उप-समस्याओं के समाधान को मिलाया जाता है।
बाइनरी खोज डिवाइड को विभाजित करने और जीतने का एक उदाहरण है।
स्यूडोकोड
Binarysearch(a, b, low, high)
if low < high then
return NOT FOUND
else
mid ← (low+high) / 2
if b = key(mid) then
return key(mid)
else if b < key(mid) then
return BinarySearch(a, b, low, mid−1)
else
return BinarySearch(a, b, mid+1, high)गहराई-पहली खोज
गहराई-पहली खोज (या डीएफएस) एक पेड़ या एक अप्रत्यक्ष ग्राफ़ डेटा संरचना की खोज के लिए एक एल्गोरिथ्म है। यहाँ, अवधारणा को शुरुआती नोड से शुरू करना है जिसे के रूप में जाना जाता हैrootऔर जहां तक संभव हो एक ही शाखा में यात्रा करें। यदि हमें कोई उत्तराधिकारी नोड के साथ एक नोड मिलता है, तो हम वापस लौटते हैं और शीर्ष के साथ जारी रखते हैं, जिसे अभी तक जाना नहीं है।
गहराई-पहली खोज के चरण
एक नोड (मूल) पर विचार करें जो पहले का दौरा नहीं किया गया है और इसे दौरा किया गया है।
पहले आसन्न उत्तराधिकारी नोड पर जाएं और इसे चिह्नित करें।
यदि माना गया नोड के सभी उत्तराधिकारी नोड पहले से ही आ चुके हैं या उसके पास कोई और उत्तराधिकारी नोड नहीं है, तो अपने मूल नोड पर वापस लौटें।
स्यूडोकोड
लश्कर v वह शीर्ष रेखा हो जहां खोज ग्राफ़ में शुरू होती है G।
DFS(G,v)
Stack S := {};
for each vertex u, set visited[u] := false;
push S, v;
while (S is not empty) do
u := pop S;
if (not visited[u]) then
visited[u] := true;
for each unvisited neighbour w of u
push S, w;
end if
end while
END DFS()पहले चौड़ाई खोजो
चौड़ाई-पहली खोज (या BFS) एक पेड़ या एक अप्रत्यक्ष ग्राफ़ डेटा संरचना की खोज के लिए एक एल्गोरिथ्म है। यहां, हम एक नोड के साथ शुरू करते हैं और फिर उसी स्तर के सभी आसन्न नोड्स पर जाते हैं और फिर अगले स्तर पर आसन्न उत्तराधिकारी नोड पर जाते हैं। इस रूप में भी जाना जाता हैlevel-by-level search।
चौड़ाई-प्रथम खोज के चरण
- रूट नोड के साथ शुरू करें, इसे चिह्नित करें।
- चूंकि रूट नोड में समान स्तर में कोई नोड नहीं है, इसलिए अगले स्तर पर जाएं।
- सभी आसन्न नोड्स पर जाएँ और उन्हें दौरा किया।
- अगले स्तर पर जाएं और सभी असंगत आसन्न नोड्स पर जाएं।
- इस प्रक्रिया को तब तक जारी रखें जब तक कि सभी नोड्स का दौरा न हो जाए।
स्यूडोकोड
लश्कर v वह शीर्ष रेखा हो जहां खोज ग्राफ़ में शुरू होती है G।
BFS(G,v)
Queue Q := {};
for each vertex u, set visited[u] := false;
insert Q, v;
while (Q is not empty) do
u := delete Q;
if (not visited[u]) then
visited[u] := true;
for each unvisited neighbor w of u
insert Q, w;
end if
end while
END BFS()बेस्ट-फर्स्ट सर्च
बेस्ट-फर्स्ट सर्च एक एल्गोरिथ्म है जो कम से कम संभव पथ में किसी लक्ष्य तक पहुंचने के लिए एक ग्राफ का पता लगाता है। बीएफएस और डीएफएस के विपरीत, बेस्ट-फर्स्ट सर्च एक मूल्यांकन फ़ंक्शन का अनुसरण करता है, यह निर्धारित करने के लिए कि कौन सा नोड अगले निशान के लिए सबसे उपयुक्त है।
सर्वश्रेष्ठ-प्रथम खोज के चरण
- रूट नोड के साथ शुरू करें, इसे चिह्नित करें।
- अगले उपयुक्त नोड का पता लगाएं और इसे चिह्नित करें।
- अगले स्तर पर जाएं और उपयुक्त नोड को ढूंढें और इसे विज़िट किया गया चिह्नित करें।
- इस प्रक्रिया को तब तक जारी रखें जब तक कि लक्ष्य पूरा न हो जाए।
स्यूडोकोड
BFS( m )
Insert( m.StartNode )
Until PriorityQueue is empty
c ← PriorityQueue.DeleteMin
If c is the goal
Exit
Else
Foreach neighbor n of c
If n "Unvisited"
Mark n "Visited"
Insert( n )
Mark c "Examined"
End procedureएक ग्राफ एक अमूर्त संकेतन है जिसका उपयोग वस्तुओं के जोड़े के बीच संबंध को दर्शाने के लिए किया जाता है। एक ग्राफ के होते हैं -
Vertices- एक ग्राफ में परस्पर जुड़ी वस्तुओं को कोने कहा जाता है। कार्यक्षेत्र के रूप में भी जाना जाता हैnodes।
Edges - किनारे वे लिंक होते हैं जो कोने को जोड़ते हैं।
रेखांकन दो प्रकार के होते हैं -
Directed graph - एक निर्देशित ग्राफ में, किनारों की दिशा होती है, यानी, किनारों को एक शीर्ष से दूसरे तक जाना होता है।
Undirected graph - एक अप्रत्यक्ष ग्राफ में, किनारों की कोई दिशा नहीं है।
ग्राफ रंग
ग्राफ रंग एक ग्राफ के शीर्षों पर रंगों को असाइन करने की एक विधि है, ताकि किसी भी दो आसन्न कोने में एक ही रंग न हो। रंग भरने की कुछ समस्याएं हैं -
Vertex coloring - ग्राफ के शीर्षों को रंगने का एक तरीका ताकि कोई भी दो आसन्न कोने समान रंग साझा न करें।
Edge Coloring - यह प्रत्येक किनारे पर एक रंग निर्दिष्ट करने की विधि है ताकि किसी भी दो आसन्न किनारों में एक ही रंग न हो।
Face coloring - यह एक प्लानर ग्राफ के प्रत्येक चेहरे या क्षेत्र को एक रंग प्रदान करता है ताकि कोई दो चेहरे जो एक समान सीमा साझा करते हैं, उनका रंग एक ही हो।
क्रोमेटिक नंबर
रंगीन संख्या एक ग्राफ को रंगने के लिए आवश्यक रंगों की न्यूनतम संख्या है। उदाहरण के लिए, निम्नलिखित ग्राफ की रंगीन संख्या 3 है।

ग्राफ रंगाई की अवधारणा को समय सारिणी, मोबाइल रेडियो फ्रीक्वेंसी असाइनमेंट, सूडुकू, रजिस्टर आवंटन और मानचित्रों के रंग तैयार करने में लागू किया जाता है।
ग्राफ रंग के लिए कदम
प्रत्येक प्रोसेसर के प्रारंभिक मान को n-आयामी सरणी में 1 पर सेट करें।
अब एक शीर्ष पर एक विशेष रंग निर्दिष्ट करने के लिए, यह निर्धारित करें कि क्या रंग पहले से ही आसन्न कोने को सौंपा गया है या नहीं।
यदि कोई प्रोसेसर आसन्न कोने में समान रंग का पता लगाता है, तो यह सरणी में 0 पर अपना मान सेट करता है।
एन 2 तुलना करने के बाद , यदि सरणी का कोई तत्व 1 है, तो यह एक वैध रंग है।
ग्राफ़ के रंग के लिए स्यूडोकोड
begin
create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
status[i0,..in-1] = 1
for j varies from 0 to n-1 do
begin
for k varies from 0 to n-1 do
begin
if aj,k=1 and ij=ikthen
status[i0,..in-1] =0
end
end
ok = ΣStatus
if ok > 0, then display valid coloring exists
else
display invalid coloring
endमिनिमल स्पैनिंग ट्री
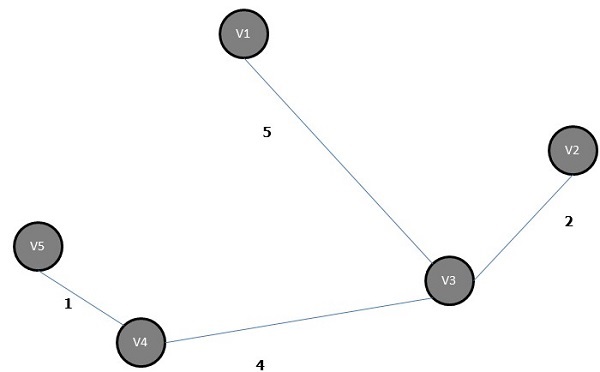
एक फैले हुए वृक्ष, जिसके सभी किनारों पर वजन (या लंबाई) का योग ग्राफ G के सभी अन्य संभावित फैले हुए वृक्षों से कम है minimal spanning tree या minimum cost spanningपेड़। निम्नलिखित आंकड़ा एक भारित जुड़ा हुआ ग्राफ दिखाता है।

उपरोक्त ग्राफ के कुछ संभावित फैले हुए पेड़ों को नीचे दिखाया गया है -



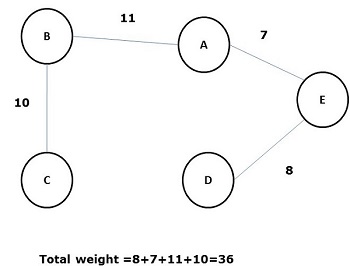



उपरोक्त सभी फैले पेड़ों के बीच, आंकड़ा (d) न्यूनतम फैले हुए पेड़ हैं। ट्रैवलिंग सेल्समैन समस्या में न्यूनतम लागत वाले फैले पेड़ की अवधारणा को लागू किया जाता है, इलेक्ट्रॉनिक सर्किट डिजाइन करना, कुशल नेटवर्क डिजाइन करना और कुशल मार्ग एल्गोरिदम डिजाइन करना।
न्यूनतम लागत फैले पेड़ को लागू करने के लिए, निम्नलिखित दो विधियों का उपयोग किया जाता है -
- प्राइम का एल्गोरिथम
- क्रुस्कल का एल्गोरिदम
प्राइम का एल्गोरिथम
प्राइम का एल्गोरिथ्म एक लालची एल्गोरिथ्म है, जो हमें एक भारित अप्रत्यक्ष ग्राफ के लिए न्यूनतम फैले हुए पेड़ को खोजने में मदद करता है। यह पहले एक शीर्ष का चयन करता है और उस शीर्ष पर सबसे कम वजन घटना के साथ एक बढ़त पाता है।
प्राइम के एल्गोरिथम के चरण
किसी भी शीर्ष का चयन करें, ग्राफ़ G का v 1 कहें ।
बढ़त का चयन करें, ई का कहना है 1 जी की ऐसी है कि ई 1 = वी 1 वी 2 और वी 1 ≠ वी 2 और ई 1 वी पर किनारों घटना में कम से कम वजन है 1 ग्राफ जी में
अब, चरण 2 के बाद, वी 2 पर न्यूनतम भारित बढ़त घटना का चयन करें ।
इसे जारी रखें जब तक n-1 किनारों को चुना नहीं गया है। यहाँn कोने की संख्या है।

न्यूनतम फैले पेड़ है -

क्रुस्कल का एल्गोरिदम
क्रुस्कल का एल्गोरिथ्म एक लालची एल्गोरिथ्म है, जो हमें एक जुड़े हुए वेटेड ग्राफ के लिए न्यूनतम फैले हुए पेड़ को खोजने में मदद करता है, जिससे प्रत्येक चरण पर बढ़ती लागत आर्क्स मिलती है। यह एक न्यूनतम-फैले पेड़ के एल्गोरिथ्म है जो कम से कम संभव वजन का एक किनारा पाता है जो जंगल में किसी भी दो पेड़ों को जोड़ता है।
क्रुशाल के एल्गोरिथ्म के चरण
न्यूनतम वजन के एक किनारे का चयन करें; कहते हैं ई 1 ग्राफ़ जी के और ई 1 एक पाश नहीं है।
ई 1 से जुड़े अगले न्यूनतम भारित किनारे का चयन करें ।
इसे जारी रखें जब तक n-1 किनारों को चुना नहीं गया है। यहाँn कोने की संख्या है।

उपरोक्त ग्राफ का न्यूनतम फैले हुए पेड़ है -
सबसे छोटा पथ एल्गोरिथम
सबसे छोटा पथ एल्गोरिथ्म स्रोत नोड (S) से गंतव्य नोड (D) तक कम से कम लागत पथ खोजने की एक विधि है। यहां, हम मूर के एल्गोरिथ्म पर चर्चा करेंगे, जिसे चौड़ाई प्रथम खोज एल्गोरिथम के रूप में भी जाना जाता है।
मूर की एल्गोरिथ्म
स्रोत शीर्ष, S को लेबल करें और उसे लेबल करें i और सेट करें i=0।
लेबल किए गए शीर्ष पर स्थित सभी अनलिस्टेड वर्टिकल खोजें i। यदि कोई कोने वर्टेक्स से जुड़े नहीं हैं, तो S, तो D, D, S से नहीं जुड़े हैं। यदि एस से जुड़े कोने हैं, तो उन्हें लेबल करेंi+1।
यदि D लेबल है, तो चरण 4 पर जाएं, अन्यथा i = i + 1 को बढ़ाने के लिए चरण 2 पर जाएं।
सबसे छोटा रास्ता मिलने के बाद रुकें।