वीएलएसआई डिज़ाइन - एमओएस ट्रांजिस्टर
पूरक MOSFET (CMOS) तकनीक आज व्यापक रूप से कई और विभिन्न अनुप्रयोगों में सर्किट बनाने के लिए उपयोग की जाती है। आज के कंप्यूटर, सीपीयू और सेल फोन कई महत्वपूर्ण लाभों के कारण सीएमओएस का उपयोग करते हैं। सीएमओएस दोनों राज्यों में कम बिजली अपव्यय, अपेक्षाकृत उच्च गति, उच्च शोर मार्जिन प्रदान करता है, और स्रोत और इनपुट वोल्टेज की एक विस्तृत श्रृंखला पर काम करेगा (बशर्ते स्रोत वोल्टेज तय हो)
जिन प्रक्रियाओं पर हम चर्चा करेंगे, उनके लिए उपलब्ध ट्रांजिस्टर का प्रकार मेटल-ऑक्साइड-सेमीकंडक्टर फील्ड इफेक्ट ट्रांजिस्टर (MOSFET) है। ये ट्रांजिस्टर बनते हैंas a ‘sandwich’एक सेमीकंडक्टर परत से मिलकर, सिलिकॉन के एक क्रिस्टल से आमतौर पर एक टुकड़ा, या वेफर; सिलिकॉन डाइऑक्साइड (ऑक्साइड) की एक परत और धातु की एक परत।
एक MOSFET की संरचना
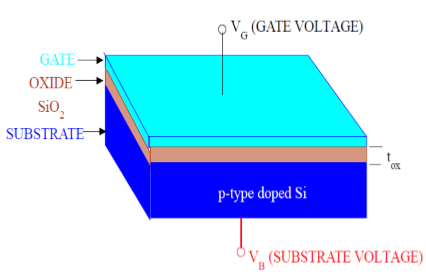
जैसा कि चित्र में दिखाया गया है, MOS संरचना में तीन परतें हैं -
The Metal Gate Electrode
The Insulating Oxide Layer (SiO2)
P – type Semiconductor (Substrate)
एमओएस संरचना एक संधारित्र बनाती है, जिसमें गेट और सब्सट्रेट दो प्लेटों और ऑक्साइड परत के रूप में ढांकता हुआ सामग्री के रूप में होते हैं। ढांकता हुआ सामग्री (SiO 2 ) की मोटाई आमतौर पर 10 एनएम और 50 एनएम के बीच होती है। सब्सट्रेट के भीतर वाहक एकाग्रता और वितरण को गेट और सब्सट्रेट टर्मिनल पर लागू बाहरी वोल्टेज द्वारा हेरफेर किया जा सकता है। अब, एमओएस की संरचना को समझने के लिए, पहले पी - टाइप सेमीकंडक्टर सब्सट्रेट के बुनियादी इलेक्ट्रिक गुणों पर विचार करें।
अर्धचालक सामग्री में वाहक की एकाग्रता हमेशा निम्नलिखित है Mass Action Law। सामूहिक कार्रवाई कानून द्वारा दिया जाता है -
$$ एनपी = n_ {मैं} ^ {2} $$
कहाँ पे,
n इलेक्ट्रॉनों की वाहक सांद्रता है
p छेद की वाहक एकाग्रता है
ni सिलिकॉन की आंतरिक वाहक सांद्रता है
अब मान लें कि सब्सट्रेट समान रूप से स्वीकर्ता (बोरॉन) सांद्रता एन ए के साथ डोप किया गया है । तो, पी-प्रकार सब्सट्रेट में इलेक्ट्रॉन और छेद एकाग्रता है
$$ n_ {पो} = \ frac {{n_ मैं} ^ {2}} {{N_ एक}} $$
$$ P_ {पो} = N_ {a} $$
यहाँ, डोपिंग एकाग्रता NA(10 15 से 10 16 सेमी ) 3 ) आंतरिक एकाग्रता एनआई से अधिक है। अब, एमओएस संरचना को समझने के लिए, पी-प्रकार सिलिकॉन सब्सट्रेट के ऊर्जा स्तर आरेख पर विचार करें।
जैसा कि चित्र में दिखाया गया है, चालन बैंड और वैलेंस बैंड के बीच बैंड अंतराल 1.1eV है। यहाँ, फ़र्मि क्षमता is F आंतरिक आंतरिक फ़र्मी स्तर (E i ) और फ़र्मी स्तर (E FP ) के बीच का अंतर है ।
जहां Fermi स्तर E F डोपिंग एकाग्रता पर निर्भर करता है। फर्मी संभावित is F आंतरिक आंतरिक स्तर (E i ) और Fermi स्तर (E FP ) के बीच का अंतर है ।
गणित के अनुसार,
$$ \ Phi_ {Fp} = \ frac {E_ {एफ} {-E_ मैं}} {q} $$
चालन बैंड और मुक्त स्थान के बीच संभावित अंतर को इलेक्ट्रॉन संबंध कहा जाता है और इसे qx द्वारा दर्शाया जाता है।
इसलिए, एक इलेक्ट्रॉन के लिए फ़र्मी स्तर से मुक्त स्थान पर जाने के लिए आवश्यक ऊर्जा को कार्य फ़ंक्शन (क्यूΦ एस ) कहा जाता है और इसके द्वारा दिया जाता है
$ $ q \ Phi _ {s} = (E_ {c} -E_ {F}) + qx $ $
निम्न आंकड़ा घटकों के ऊर्जा बैंड आरेख को दिखाता है जो एमओएस बनाते हैं।
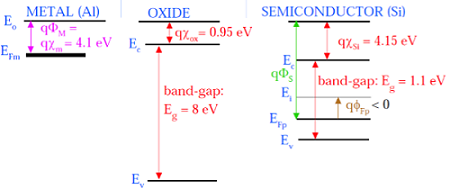
जैसा कि ऊपर चित्र में दिखाया गया है, SiO 2 परत को इन्सुलेट करने पर 8eV की बड़ी ऊर्जा बैंड गैप होती है और कार्य फ़ंक्शन 0.95 eV होता है। मेटल गेट में 4.1eV का कार्य कार्य है। यहां, कार्य फ़ंक्शन अलग हैं, इसलिए यह एमओएस सिस्टम में वोल्टेज ड्रॉप बनाएगा। नीचे दिया गया आंकड़ा MOS सिस्टम के संयुक्त ऊर्जा बैंड आरेख को दर्शाता है।
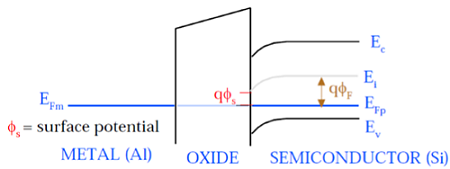
जैसा कि इस आंकड़े में दिखाया गया है, धातु के गेट और सेमीकंडक्टर (Si) के फर्मी संभावित स्तर समान क्षमता पर हैं। सतह पर फर्मी क्षमता को सतह की क्षमता it S कहा जाता है और यह परिमाण में Fermi की संभावित in F से छोटी होती है ।
एक MOSFET का कार्य करना
MOSFET में MOS कैपेसिटर होते हैं, जो दो pn जंक्शनों के साथ चैनल क्षेत्र में बंद होते हैं और इस क्षेत्र को गेट वोल्टेज द्वारा नियंत्रित किया जाता है। दोनों जंक्शन जंक्शन को पक्षपाती बनाने के लिए, सब्सट्रेट क्षमता को अन्य तीन टर्मिनलों की क्षमता से कम रखा जाता है।
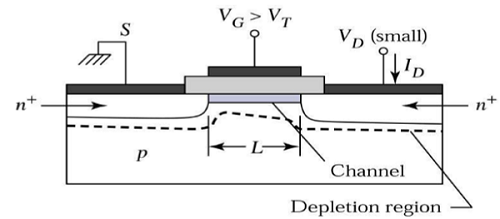
यदि थ्रेशोल्ड वोल्टेज (V GS > V TO ) से परे गेट वोल्टेज को बढ़ाया जाएगा , तो सतह पर व्युत्क्रम परत स्थापित की जाएगी और स्रोत और नाली के बीच n-type चैनल का गठन किया जाएगा। यह n- टाइप चैनल V DS मान के अनुसार ड्रेन करंट को ले जाएगा ।
V DS के विभिन्न मानों के लिए , MOSFET को विभिन्न क्षेत्रों में संचालित किया जा सकता है जैसा कि नीचे बताया गया है।
रैखिक क्षेत्र
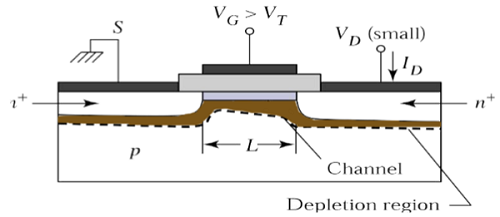
वी डी एस = 0 पर, थर्मल संतुलन उलटा चैनल क्षेत्र में मौजूद है और नाली वर्तमान I D = 0. अब यदि छोटे नाली वोल्टेज, V DS > 0 को लागू किया जाता है, तो V DS का आनुपातिक प्रवाह स्रोत से प्रवाहित होने लगेगा चैनल के माध्यम से नाली।
चैनल स्रोत से नाली तक प्रवाह के लिए एक निरंतर मार्ग देता है। ऑपरेशन के इस मोड को कहा जाता हैlinear region। एक एन-चैनल MOSFET का क्रॉस सेक्शनल व्यू, रेखीय क्षेत्र में काम कर रहा है, जो नीचे दिए गए चित्र में दिखाया गया है।
संतृप्ति क्षेत्र के किनारे पर
अब अगर वी डीएस बढ़ा दिया जाता है, तो नाले के अंत में चैनल और चैनल की गहराई में प्रभार कम हो जाते हैं। वी डीएस = वी डीएसएटी के लिए , चैनल में प्रभार शून्य हो जाता है, जिसे कहा जाता हैpinch – off point। संतृप्ति क्षेत्र के किनारे पर संचालित n-चैनल MOSFET का क्रॉस सेक्शनल दृश्य नीचे दिए गए चित्र में दिखाया गया है।
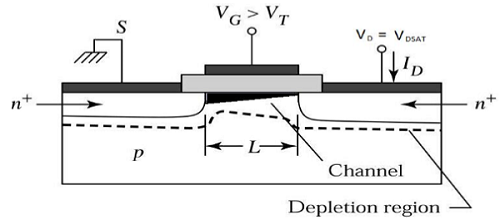
संतृप्ति क्षेत्र
वी डीएस > वी डीएसएटी के लिए , एक खाली सतह नाली के पास बनती है, और नाली वोल्टेज बढ़ने से यह कम हो गया क्षेत्र स्रोत तक फैल जाता है।
ऑपरेशन के इस मोड को कहा जाता है Saturation region। स्रोत से चैनल अंत तक आने वाले इलेक्ट्रॉनों, नाली में कमी क्षेत्र में प्रवेश करते हैं और उच्च विद्युत क्षेत्र में नाली की ओर त्वरित होते हैं।
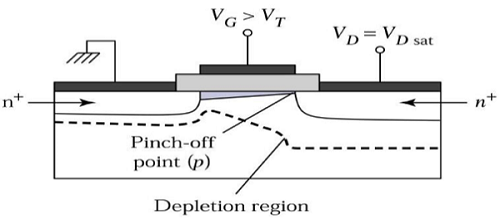
MOSFET वर्तमान - वोल्टेज विशेषताओं
MOSFET की वर्तमान - वोल्टेज विशेषता को समझने के लिए, चैनल के लिए सन्निकटन किया जाता है। इस सन्निकटन के बिना, MOS प्रणाली के तीन आयाम विश्लेषण जटिल हो जाते हैं। Gradual Channel Approximation (GCA) वर्तमान के लिए - वोल्टेज विशेषता विश्लेषण समस्या को कम करेगा।
क्रमिक चैनल अनुमोदन (GCA)
रैखिक मोड में संचालित n चैनल MOSFET के क्रॉस अनुभागीय दृश्य पर विचार करें। यहां, स्रोत और सब्सट्रेट जमीन से जुड़े हुए हैं। V S = V B = 0. गेट - टू-सोर्स (V GS ) और ड्रेन-टू-सोर्स वोल्टेज (V DS ) वोल्टेज बाहरी पैरामीटर हैं जो ड्रेन करंट I D को नियंत्रित करते हैं ।
वोल्टेज, वी जीएस थ्रेशोल्ड वोल्टेज वी टू से अधिक वोल्टेज पर सेट किया जाता है , ताकि स्रोत और नाली के बीच एक चैनल बनाया जा सके। जैसा कि चित्र में दिखाया गया है, x - दिशा सतह के लंबवत है और y - दिशा सतह के समानांतर है।
यहाँ, y = 0 स्रोत के अंत में जैसा कि चित्र में दिखाया गया है। स्रोत के संबंध में चैनल वोल्टेज, द्वारा दर्शाया गया हैVC(Y)। मान लें कि थ्रेसहोल्ड वोल्टेज VTO चैनल क्षेत्र के साथ स्थिर है, y = 0 से y = L के बीच। चैनल वोल्टेज V C के लिए सीमा स्थिति है -
$ $ V_ {c} \ बाएँ (y = 0 \ दाएँ) = V_ {s} = 0 \, और \, V_ {c} \ बाएँ (y = L \ दाएँ) = V_ {DS} $ $
हम भी ऐसा मान सकते हैं
$ $ V_ {GS} \ geq V_ {TO} $ $ और
$ $ V_ {GD} = V_ {GS} -V_ {DS} \ geq V_ {TO} $ $
बता दें Q1 (y) सतह उलटा परत में कुल मोबाइल इलेक्ट्रॉन चार्ज है। इस इलेक्ट्रॉन आवेश को इस प्रकार व्यक्त किया जा सकता है -
$$ Q1 (y) = - C_ {बैल} [V_ {जी एस} {-V_ सी (वाई)} - V_ {को}]। $$
नीचे दिया गया आंकड़ा सतह उलटा परत की स्थानिक ज्यामिति को दर्शाता है और इसके आयामों को इंगित करता है। जैसे-जैसे हम नाले से स्रोत की ओर बढ़ते हैं, उलटा लेयर टेंपर ऑफ हो जाता है। अब, यदि हम चैनल लंबाई L के छोटे क्षेत्र के रंग पर विचार करते हैं तो इस क्षेत्र द्वारा दी जाने वाली वृद्धिशील प्रतिरोध dR को निम्न के रूप में व्यक्त किया जा सकता है -
$ $ dR = - \ frac {डाई} {w। \ mu _ {n} .Q1 (y)} $ $
यहां, शून्य से व्युत्क्रम परत आवेश Q1 और μ n की नकारात्मक ध्रुवीयता के कारण ऋण चिन्ह है , जो निरंतर है। अब, dR समीकरण में Q1 (y) के मान को प्रतिस्थापित करें -
$ $ dR = - \ frac {dy} {w। \ mu _ {n}। \ left \ {-C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right ] -V_ {TO} \ right \}} $ $
$$ dR = \ frac {डाई} {w। \ _ mu {{}} .C_ {बैल} \ _ छोड़ दिया [V_ {GS} -V_ {C \ बाएँ (Y \ दाएँ)} \ सही] -वी_ {TO} } $$
अब छोटे डाई क्षेत्र में वोल्टेज ड्रॉप द्वारा दिया जा सकता है
$$ dV_ {c} = I_ {D} .dR $$
उपरोक्त समीकरण में dR का मान रखें
$ $ dV_ {C} = I_ {D}। \ frac {dy} {w।। mu {{n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} \ right] -V_ {को}} $$
$ $ w। \ mu _ {n} .C_ {बैल} \ _ [V_ {GS} -V_ {C (Y)} - V_ {TO} \ right] .dV_ {C} = I_ {D} .dy। $$
पूरे चैनल क्षेत्र पर ड्रेन करंट आईडी प्राप्त करने के लिए, उपरोक्त समीकरण को चैनल के साथ y = 0 से y = L तक एकीकृत किया जा सकता है और V C (y) = 0 से V C (y) = V DS ,
$ $ C_ {बैल} .w। \ Mu _ {n}। \ Int_ {V_ {c} = 0} ^ {V_ {DS}} \ left [V_ {GS} -V_ {C \ left (Y दाएँ) )} - V_ {TO} \ right] .dV_ {C} = \ int_ {Y = 0} ^ {L} I_ {D} .dy $ $।
$$ \ frac {C_ {ox} .w। \ mu _ {n}} {2} \ left (2 \ बाएँ [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ सही) = I_ {D} \ left [L-0 \ right] $$
$ $ I_ {D} = \ frac {C_ {ox}। Mu _ {n}} {2}। \ Frac {w} {L} \ left (2 \ left [V_ {GS} -V_ {TO) \ right] V_ {DS} -V_ {DS} ^ {2} \ right) $$
रैखिक क्षेत्र के लिए V DS <V GS - V TO । संतृप्ति क्षेत्र के लिए, V DS का मान (V GS - V TO ) से बड़ा है । इसलिए, संतृप्ति क्षेत्र V DS = (V GS - V TO ) के लिए।
$ $ I_ {D} = C_ {बैल}। \ _ mu {{}}। \ _ Frac {w} {2} \ _ \ _ (frac {\ _ बाईं ओर [2V_ {DS} \ right] V_ {DS} -V_ { DS} ^ {2}} {L} \ right) $$
$ $ I_ {D} = C_ {बैल}। \ mu _ {n}। \ Frac {w} {2} \ _ \ _ (\ frac {2V_ {DS} ^ {2} -V_ {DS} ^ [2]} } {L} \ right) $ $
$ $ I_ {D} = C_ {बैल}। \ _ mu {{}}। \ _ Frac {w} {2} \ _ \ _ (frac {V_ {DS} ^ {2}} {L} \ right) $ $
$ $ I_ {D} = C_ {बैल}। \ _ mu {{}}। \ _ Frac {w} {2} \ _ \ _ (frac {\ _ left [V_ {GS} -V_ {TO} \ right] ^ {} 2}} {L} \ right) $ $