Koneksi Sirkuit di Kapasitor
Dalam sebuah rangkaian, Kapasitor dapat dihubungkan secara seri atau paralel. Jika satu set kapasitor dihubungkan dalam suatu rangkaian, jenis sambungan kapasitor berhubungan dengan nilai tegangan dan arus dalam jaringan tersebut.
Kapasitor dalam Seri
Mari kita amati apa yang terjadi, ketika beberapa Kapasitor dihubungkan secara Seri. Mari kita pertimbangkan tiga kapasitor dengan nilai berbeda, seperti yang ditunjukkan pada gambar di bawah ini.

Kapasitansi
Ketika kapasitansi jaringan yang kapasitor seri dianggap, kebalikan dari kapasitansi semua kapasitor, ditambahkan untuk mendapatkan kebalikan dari total kapasitansi. Untuk mendapatkan ini lebih jelas,
$$ \ frac {1} {C_ {T}} \: \: = \: \: \ frac {1} {C_ {1}} \: \: + \: \: \ frac {1} {C_ { 2}} \: \: + \: \: \ frac {1} {C_ {3}} $$
Mengikuti rumus yang sama, jika hanya dua kapasitor yang dihubungkan secara seri, maka
$$ C_ {T} \: \: = \: \: \ frac {C_ {1} \: \: \ times \: \: C_ {2}} {C_ {1} \: \: + \: \ : C_ {2}} $$
Di mana C 1 adalah kapasitansi melintasi 1 st kapasitor, C 2 adalah kapasitansi melintasi 2 nd kapasitor dan C 3 adalah kapasitansi melintasi 3 rd kapasitor di jaringan di atas.
Tegangan
Tegangan di setiap kapasitor tergantung pada nilai kapasitansi individu. Yang berarti
$$ V_ {C1} \: \: = \: \: \ frac {Q_ {T}} {C_ {1}} \: \: V_ {C2} \: \: = \: \: \ frac {Q_ {T}} {C_ {2}} \: \: V_ {C3} \: \: = \: \: \ frac {Q_ {T}} {C_ {3}} $$
Tegangan total di rangkaian kapasitor seri,
$$ V_ {T} \: \: = \: \: V_ {C1} \: \: + \: \: V_ {C2} \: \: + \: \: V_ {C3} $$
Dimana V c1 adalah tegangan 1 st kapasitor, V c2 adalah tegangan 2 nd kapasitor dan V c3 adalah tegangan 3 rd kapasitor di jaringan di atas.
Arus
Jumlah total Arus yang mengalir melalui satu set Kapasitor yang terhubung secara seri adalah sama di semua titik. Oleh karena itu kapasitor akan menyimpan jumlah muatan yang sama terlepas dari nilai kapasitansinya.
Saat ini melalui jaringan,
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Dimana saya 1 adalah arus melalui 1 st kapasitor, saya 2 adalah arus melalui 2 nd kapasitor dan saya 3 adalah arus melalui 3 rd kapasitor di jaringan di atas.
Karena arusnya sama, penyimpanan muatannya sama karena setiap pelat kapasitor mendapat muatannya dari kapasitor yang berdekatan dan karenanya kapasitor secara seri akan memiliki muatan yang sama.
$$ Q_ {T} \: \: = \: \: Q_ {1} \: \: = \: \: Q_ {2} \: \: = \: \: Q_ {3} $$
Kapasitor secara Paralel
Mari kita amati apa yang terjadi, ketika beberapa kapasitor dihubungkan secara Paralel. Mari kita pertimbangkan tiga kapasitor dengan nilai berbeda, seperti yang ditunjukkan pada gambar di bawah ini.
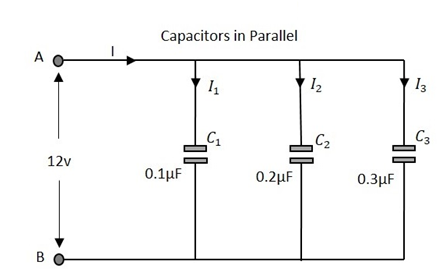
Kapasitansi
Kapasitansi total rangkaian sama dengan jumlah kapasitansi individu kapasitor di jaringan.
$$ C_ {T} \: \: = \: \: C_ {1} \: \: + \: \: C_ {2} \: \: + \: \: C_ {3} $$
Di mana C 1 adalah kapasitansi melintasi 1 st kapasitor, C 2 adalah kapasitansi melintasi 2 nd kapasitor dan C 3 adalah kapasitansi melintasi 3 rd kapasitor di jaringan di atas.
Tegangan
Tegangan yang diukur di ujung rangkaian adalah same sebagai tegangan di semua kapasitor yang terhubung dalam rangkaian paralel.
$$ V_ {T} \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
Dimana V c1 adalah tegangan 1 st kapasitor, V c2 adalah tegangan 2 nd kapasitor dan V c3 adalah tegangan 3 rd kapasitor di jaringan di atas.
Arus
Arus total yang mengalir sama dengan jumlah arus yang mengalir melalui setiap kapasitor yang terhubung pada jaringan paralel.
$$ I_ {T} \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Dimana saya 1 adalah arus melalui 1 st kapasitor, saya 2 adalah arus melalui 2 nd kapasitor dan saya 3 adalah arus melalui 3 rd kapasitor di jaringan di atas.