Big Data Analytics - Metode Statistik

Saat menganalisis data, dimungkinkan untuk memiliki pendekatan statistik. Alat dasar yang diperlukan untuk melakukan analisis dasar adalah -

• Analisis korelasi
• Analisis Varians
• Pengujian Hipotesis

Saat bekerja dengan kumpulan data besar, itu tidak melibatkan masalah karena metode ini tidak intensif secara komputasi dengan pengecualian Analisis Korelasi. Dalam hal ini, selalu memungkinkan untuk mengambil sampel dan hasilnya harus kuat.

Analisis korelasi

Analisis Korelasi berusaha menemukan hubungan linier antara variabel numerik. Ini dapat berguna dalam situasi yang berbeda. Salah satu penggunaan yang umum adalah analisis data eksplorasi, di bagian 16.0.2 buku ini terdapat contoh dasar dari pendekatan ini. Pertama-tama, metrik korelasi yang digunakan dalam contoh yang disebutkan didasarkan padaPearson coefficient. Namun ada, metrik korelasi menarik lainnya yang tidak dipengaruhi oleh pencilan. Metrik ini disebut korelasi spearman.

Itu spearman correlation metrik lebih kuat terhadap keberadaan pencilan daripada metode Pearson dan memberikan perkiraan yang lebih baik dari hubungan linier antara variabel numerik ketika data tidak terdistribusi normal.

library(ggplot2)

# Select variables that are interesting to compare pearson and spearman 
correlation methods. 
x = diamonds[, c('x', 'y', 'z', 'price')]  

# From the histograms we can expect differences in the correlations of both 
metrics.  
# In this case as the variables are clearly not normally distributed, the 
spearman correlation 

# is a better estimate of the linear relation among numeric variables. 
par(mfrow = c(2,2)) 
colnm = names(x) 
for(i in 1:4) { 
   hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i])) 
} 
par(mfrow = c(1,1))

Dari histogram pada gambar berikut, kita dapat mengharapkan perbedaan korelasi kedua metrik tersebut. Dalam hal ini, karena variabel jelas tidak terdistribusi normal, korelasi spearman adalah perkiraan yang lebih baik dari hubungan linier antar variabel numerik.

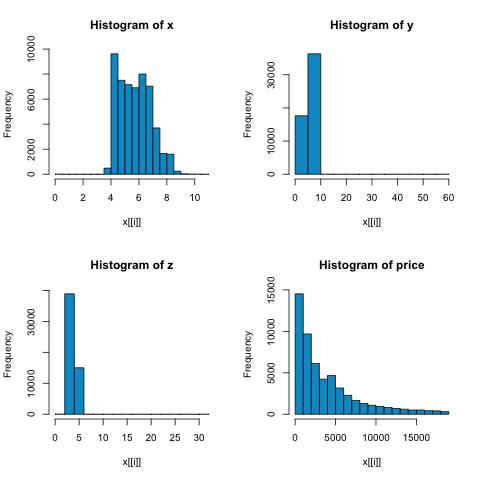
Untuk menghitung korelasi di R, buka file bda/part2/statistical_methods/correlation/correlation.R yang memiliki bagian kode ini.

## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson') 
cor_spearman <- cor(x, method = 'spearman')  

### Pearson Correlation 
print(cor_pearson) 
#            x          y          z        price 
# x      1.0000000  0.9747015  0.9707718  0.8844352 
# y      0.9747015  1.0000000  0.9520057  0.8654209 
# z      0.9707718  0.9520057  1.0000000  0.8612494 
# price  0.8844352  0.8654209  0.8612494  1.0000000  

### Spearman Correlation 
print(cor_spearman) 
#              x          y          z      price 
# x      1.0000000  0.9978949  0.9873553  0.9631961 
# y      0.9978949  1.0000000  0.9870675  0.9627188 
# z      0.9873553  0.9870675  1.0000000  0.9572323 
# price  0.9631961  0.9627188  0.9572323  1.0000000

Uji Chi-squared

Uji chi-squared memungkinkan kita untuk menguji apakah dua variabel acak tidak bergantung. Artinya distribusi probabilitas masing-masing variabel tidak mempengaruhi variabel lainnya. Untuk mengevaluasi tes di R, pertama kita perlu membuat tabel kontingensi, dan kemudian meneruskan tabel kechisq.test R fungsi.

Sebagai contoh, mari kita periksa apakah ada hubungan antara variabel: cut dan color dari dataset diamonds. Tes ini secara resmi didefinisikan sebagai -

• H0: Potongan variabel dan berlian bersifat independen
• H1: Potongan variabel dan berlian tidak independen

Kami akan mengasumsikan ada hubungan antara kedua variabel ini dengan namanya, tetapi pengujian dapat memberikan "aturan" objektif yang mengatakan seberapa signifikan hasil ini atau tidak.

Dalam potongan kode berikut, kami menemukan bahwa nilai-p pengujian adalah 2.2e-16, ini hampir nol dalam istilah praktis. Kemudian setelah menjalankan pengujian melakukan aMonte Carlo simulation, kami menemukan bahwa p-value adalah 0,0004998 yang masih cukup rendah dari ambang 0,05. Hasil ini berarti kami menolak hipotesis nol (H0), jadi kami percaya variabelcut dan color tidak independen.

library(ggplot2)

# Use the table function to compute the contingency table 
tbl = table(diamonds$cut, diamonds$color) 
tbl  

#              D    E    F    G    H    I    J 
# Fair       163  224  312  314  303  175  119 
# Good       662  933  909  871  702  522  307 
# Very Good 1513 2400 2164 2299 1824 1204  678 
# Premium   1603 2337 2331 2924 2360 1428  808 
# Ideal     2834 3903 3826 4884 3115 2093  896  

# In order to run the test we just use the chisq.test function. 
chisq.test(tbl)  

# Pearson’s Chi-squared test 
# data:  tbl 
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation 
# It's needed to add the simulate.p.value = TRUE flag and the amount of 
simulations 
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)  

# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates) 
# data:  tbl 
# X-squared = 310.32, df = NA, p-value = 0.0004998

Uji-t

Ide t-testadalah untuk mengevaluasi apakah ada perbedaan dalam distribusi variabel numerik # antara kelompok variabel nominal yang berbeda. Untuk mendemonstrasikan ini, saya akan memilih level level Adil dan Ideal dari pemotongan variabel faktor, kemudian kami akan membandingkan nilai variabel numerik di antara kedua kelompok tersebut.

data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]

data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the 
cut variable 
df1 = data[, c('cut', 'price')]  

# We can see the price means are different for each group 
tapply(df1$price, df1$cut, mean) 
# Fair    Ideal  
# 4358.758 3457.542

Uji-t diimplementasikan di R dengan t.testfungsi. Antarmuka rumus ke t.test adalah cara paling sederhana untuk menggunakannya, idenya adalah variabel numerik dijelaskan oleh variabel grup.

Sebagai contoh: t.test(numeric_variable ~ group_variable, data = data). Dalam contoh sebelumnya, filenumeric_variable adalah price dan group_variable adalah cut.

Dari perspektif statistik, kami menguji apakah ada perbedaan dalam distribusi variabel numerik di antara dua kelompok. Secara formal pengujian hipotesis dijelaskan dengan hipotesis nol (H0) dan hipotesis alternatif (H1).

• H0: Tidak ada perbedaan dalam distribusi variabel harga antara kelompok Adil dan Ideal

• H1 Terdapat perbedaan distribusi variabel harga antara kelompok Wajar dan Ideal

Berikut ini dapat diimplementasikan di R dengan kode berikut -

t.test(price ~ cut, data = data)

# Welch Two Sample t-test 
#  
# data:  price by cut 
# t = 9.7484, df = 1894.8, p-value < 2.2e-16 
# alternative hypothesis: true difference in means is not equal to 0 
# 95 percent confidence interval: 
#   719.9065 1082.5251 
# sample estimates: 
#   mean in group Fair mean in group Ideal  
#   4358.758            3457.542   

# Another way to validate the previous results is to just plot the 
distributions using a box-plot 
plot(price ~ cut, data = data, ylim = c(0,12000),  
   col = 'deepskyblue3')

Kita dapat menganalisis hasil pengujian dengan memeriksa apakah nilai p lebih rendah dari 0,05. Jika demikian, kami menyimpan hipotesis alternatif. Ini berarti kami telah menemukan perbedaan harga di antara dua tingkat faktor potong. Berdasarkan nama level, kami mengharapkan hasil ini, tetapi kami tidak berharap bahwa harga rata-rata di grup Gagal akan lebih tinggi daripada di grup Ideal. Kita dapat melihat ini dengan membandingkan rata-rata setiap faktor.

Itu plotperintah menghasilkan grafik yang menunjukkan hubungan antara harga dan variabel potong. Ini adalah plot kotak; kami telah membahas plot ini di bagian 16.0.1 tetapi pada dasarnya menunjukkan distribusi variabel harga untuk dua tingkat pemotongan yang kami analisis.

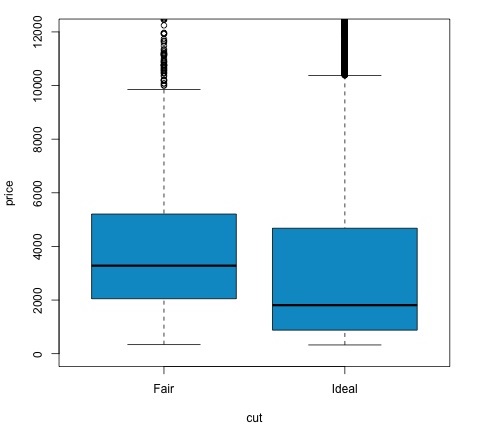
Analisis Varians

Analysis of Variance (ANOVA) adalah model statistik yang digunakan untuk menganalisis perbedaan antar distribusi kelompok dengan membandingkan mean dan varians tiap kelompok, model yang dikembangkan oleh Ronald Fisher. ANOVA memberikan uji statistik apakah rata-rata beberapa kelompok sama atau tidak, dan oleh karena itu menggeneralisasi uji-t ke lebih dari dua kelompok.

ANOVA berguna untuk membandingkan tiga atau lebih kelompok untuk signifikansi statistik karena melakukan beberapa uji-t dua sampel akan menghasilkan peningkatan kemungkinan melakukan kesalahan tipe I statistik.

Dalam rangka memberikan penjelasan matematis, berikut ini diperlukan untuk memahami soal tes.

x _ij = x + (x _i - x) + (x _ij - x)

Ini mengarah ke model berikut -

x _ij = μ + α _i + ∈ _ij

di mana μ adalah mean grand dan α _i adalah mean grup ke-i. Suku kesalahan ∈ _ij diasumsikan iid dari distribusi normal. Hipotesis nol dari pengujian ini adalah -

α ₁ = α ₂ =… = α _k

Dalam hal menghitung statistik uji, kita perlu menghitung dua nilai -

• Jumlah kuadrat untuk perbedaan kelompok -

$$ SSD_B = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {i}}} - \ bar {x}) ^ 2 $$

• Jumlah kotak dalam kelompok

$$ SSD_W = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {ij}}} - \ bar {x _ {\ bar {i}}}) ^ 2 $$

dengan SSD _B memiliki derajat kebebasan k − 1 dan SSD _W memiliki derajat kebebasan N − k. Kemudian kita dapat menentukan perbedaan kuadrat rata-rata untuk setiap metrik.

MS _B = SSD _B / (k - 1)

MS _w = SSD _w / (N - k)

Akhirnya, statistik uji dalam ANOVA didefinisikan sebagai rasio dari dua besaran di atas

F = MS _B / MS _w

yang mengikuti distribusi F dengan k − 1 dan N − k derajat kebebasan. Jika hipotesis nol benar, F kemungkinan akan mendekati 1. Jika tidak, MSB kuadrat rata-rata antara kelompok cenderung besar, yang menghasilkan nilai F yang besar.

Pada dasarnya, ANOVA memeriksa dua sumber dari varian total dan melihat bagian mana yang berkontribusi lebih. Inilah mengapa disebut analisis varians meskipun tujuannya adalah untuk membandingkan rata-rata kelompok.

Dalam hal menghitung statistik, sebenarnya cukup mudah dilakukan di R. Contoh berikut akan menunjukkan bagaimana hal itu dilakukan dan memplot hasilnya.

library(ggplot2)
# We will be using the mtcars dataset 

head(mtcars) 
#                    mpg  cyl disp  hp drat  wt  qsec   vs am  gear carb 
# Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4 
# Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4 
# Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1 
# Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1 
# Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2 
# Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1  

# Let's see if there are differences between the groups of cyl in the mpg variable. 
data = mtcars[, c('mpg', 'cyl')]  
fit = lm(mpg ~ cyl, data = mtcars) 
anova(fit)  

# Analysis of Variance Table 
# Response: mpg 
#           Df Sum Sq Mean Sq F value    Pr(>F)     
# cyl        1 817.71  817.71  79.561 6.113e-10 *** 
# Residuals 30 308.33   10.28 
# Signif. codes:  0 *** 0.001 ** 0.01 * 0.05 . 
# Plot the distribution 
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')

Kode akan menghasilkan keluaran berikut -

Nilai p yang kita dapatkan dalam contoh secara signifikan lebih kecil dari 0,05, jadi R mengembalikan simbol '***' untuk menunjukkan ini. Ini berarti kami menolak hipotesis nol dan kami menemukan perbedaan antara rata-rata mpg di antara kelompok-kelompok yang berbedacyl variabel.