Desain Penyusun - Analisis Sintaks

Analisis sintaks atau parsing adalah tahap kedua dari sebuah compiler. Dalam bab ini, kita akan mempelajari konsep dasar yang digunakan dalam konstruksi parser.

Kita telah melihat bahwa penganalisis leksikal dapat mengidentifikasi token dengan bantuan ekspresi reguler dan aturan pola. Tetapi penganalisis leksikal tidak dapat memeriksa sintaks dari kalimat yang diberikan karena keterbatasan ekspresi reguler. Ekspresi reguler tidak dapat memeriksa token penyeimbang, seperti tanda kurung. Oleh karena itu, fase ini menggunakan tata bahasa bebas konteks (CFG), yang dikenali oleh automata push-down.

CFG, di sisi lain, adalah superset Tata Bahasa Reguler, seperti yang digambarkan di bawah ini:

Ini menyiratkan bahwa setiap Tata Bahasa Reguler juga bebas konteks, tetapi terdapat beberapa masalah, yang berada di luar cakupan Tata Bahasa Reguler. CFG adalah alat yang berguna untuk menjelaskan sintaks bahasa pemrograman.

Tata Bahasa Bebas Konteks

Pada bagian ini, pertama-tama kita akan melihat definisi tata bahasa bebas konteks dan memperkenalkan terminologi yang digunakan dalam teknologi parsing.

Tata bahasa tanpa konteks memiliki empat komponen:

Satu set non-terminals(V). Non-terminal adalah variabel sintaksis yang menunjukkan kumpulan string. Non-terminal mendefinisikan set string yang membantu mendefinisikan bahasa yang dihasilkan oleh tata bahasa.
Satu set token, yang dikenal sebagai terminal symbols(Σ). Terminal adalah simbol dasar dari mana string terbentuk.
Satu set productions(P). Produksi tata bahasa menentukan cara di mana terminal dan non-terminal dapat digabungkan untuk membentuk string. Setiap produksi terdiri dari anon-terminal disebut sisi kiri produksi, panah, dan urutan token dan / atau on- terminals, yang disebut sisi kanan produksi.
Salah satu non-terminal ditetapkan sebagai simbol start (S); dari tempat produksi dimulai.

Senar diturunkan dari simbol awal dengan berulang kali mengganti non-terminal (awalnya simbol awal) dengan sisi kanan produksi, untuk non-terminal tersebut.

Contoh

Kami mengambil masalah bahasa palindrome, yang tidak bisa dijelaskan dengan Regular Expression. Artinya, L = {w | w = w ^R } bukan bahasa biasa. Tapi itu bisa dijelaskan melalui CFG, seperti diilustrasikan di bawah ini:

G = ( V, Σ, P, S )

Dimana:

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

Tata bahasa ini menjelaskan bahasa palindrome, seperti: 1001, 11100111, 00100, 1010101, 11111, dll.

Penganalisis Sintaks

Penganalisis atau pengurai sintaks mengambil masukan dari penganalisis leksikal dalam bentuk aliran token. Parser menganalisis kode sumber (aliran token) terhadap aturan produksi untuk mendeteksi kesalahan apa pun dalam kode. Output dari fase ini adalah aparse tree.

Dengan cara ini, parser menyelesaikan dua tugas, yaitu mem-parsing kode, mencari kesalahan, dan menghasilkan pohon parse sebagai output dari fase.

Parser diharapkan mengurai seluruh kode meskipun ada beberapa kesalahan dalam program. Parser menggunakan strategi pemulihan kesalahan, yang akan kita pelajari nanti di bab ini.

Penurunan

Derivasi pada dasarnya adalah urutan aturan produksi, untuk mendapatkan string input. Selama penguraian, kami mengambil dua keputusan untuk beberapa bentuk masukan sentensial:

Memutuskan non-terminal mana yang akan diganti.
Menentukan aturan produksi, yang mana, non-terminal akan diganti.

Untuk memutuskan non-terminal mana yang akan diganti dengan aturan produksi, kita dapat memiliki dua opsi.

Penurunan paling kiri

Jika bentuk sentensial dari suatu masukan dipindai dan diganti dari kiri ke kanan, itu disebut derivasi paling kiri. Bentuk sentensial yang diturunkan oleh derivasi paling kiri disebut bentuk sentensial kiri.

Penurunan Paling Kanan

Jika kita memindai dan mengganti input dengan aturan produksi, dari kanan ke kiri, ini dikenal sebagai derivasi paling kanan. Bentuk sentensial yang diturunkan dari derivasi paling kanan disebut bentuk sentensial-kanan.

Example

Aturan produksi:

E → E + E
E → E * E
E → id

String masukan: id + id * id

Derivasi paling kiri adalah:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

Perhatikan bahwa non-terminal sisi paling kiri selalu diproses terlebih dahulu.

Derivasi paling kanan adalah:

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

Parse Tree

Pohon parse adalah penggambaran grafis dari suatu derivasi. Mudah untuk melihat bagaimana string diturunkan dari simbol awal. Simbol awal penurunan menjadi akar pohon parse. Mari kita lihat ini dengan contoh dari topik terakhir.

Kami mengambil turunan paling kiri dari a + b * c

Derivasi paling kiri adalah:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
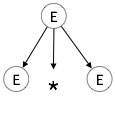
E → id + id * id

Langkah 1:

E → E * E

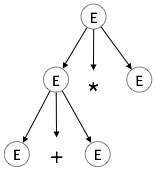
Langkah 2:

E → E + E * E

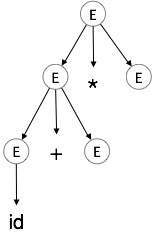
Langkah 3:

E → id + E * E

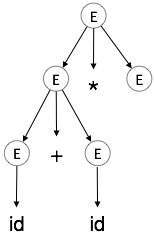
Langkah 4:

E → id + id * E

Langkah 5:

E → id + id * id

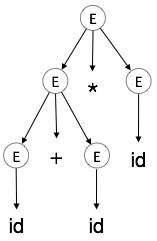
Di pohon parse:

Semua simpul daun adalah terminal.
Semua node interior adalah non-terminal.
Traversal berurutan memberikan string input asli.

Pohon parse menggambarkan asosiasi dan prioritas operator. Sub-pohon terdalam dilintasi terlebih dahulu, oleh karena itu operator dalam sub-pohon tersebut diutamakan daripada operator yang ada di simpul induk.

Kemenduaan

Tata bahasa G dikatakan ambigu jika memiliki lebih dari satu pohon parse (derivasi kiri atau kanan) untuk setidaknya satu string.

Example

E → E + E
E → E – E
E → id

Untuk string id + id - id, tata bahasa di atas menghasilkan dua pohon parse:

Bahasa yang dihasilkan oleh tata bahasa yang ambigu dikatakan demikian inherently ambiguous. Ambiguitas dalam tata bahasa tidak baik untuk konstruksi compiler. Tidak ada metode yang dapat mendeteksi dan menghapus ambiguitas secara otomatis, tetapi metode ini dapat dihilangkan dengan menulis ulang seluruh tata bahasa tanpa ambiguitas, atau dengan menyetel dan mengikuti batasan asosiatif dan prioritas.

Asosiatif

Jika operand memiliki operator di kedua sisi, sisi tempat operator mengambil operan ini ditentukan oleh asosiasi operator tersebut. Jika operasinya adalah kiri-asosiatif, maka operan akan diambil oleh operator kiri atau jika operasinya adalah asosiasi kanan, operator kanan akan mengambil operan.

Example

Operasi seperti Penjumlahan, Perkalian, Pengurangan, dan Pembagian dibiarkan asosiatif. Jika ekspresi tersebut mengandung:

id op id op id

itu akan dievaluasi sebagai:

(id op id) op id

Misalnya, (id + id) + id

Operasi seperti Eksponen adalah asosiatif yang benar, yaitu urutan evaluasi dalam ekspresi yang sama adalah:

id op (id op id)

Misalnya, id ^ (id ^ id)

Hak lebih tinggi

Jika dua operator berbeda berbagi operan yang sama, prioritas operator memutuskan operator mana yang akan mengambil operan. Artinya, 2 + 3 * 4 dapat memiliki dua pohon parsing yang berbeda, satu sesuai dengan (2 + 3) * 4 dan lainnya sesuai dengan 2+ (3 * 4). Dengan menetapkan prioritas di antara operator, masalah ini dapat dengan mudah dihilangkan. Seperti pada contoh sebelumnya, secara matematis * (perkalian) didahulukan dari + (penjumlahan), sehingga ekspresi 2 + 3 * 4 akan selalu diartikan sebagai:

2 + (3 * 4)

Metode ini mengurangi kemungkinan ambiguitas dalam suatu bahasa atau tata bahasanya.

Rekursi Kiri

Sebuah tata bahasa menjadi rekursif kiri jika ia memiliki non-terminal 'A' yang derivasi mengandung 'A' itu sendiri sebagai simbol paling kiri. Tata bahasa rekursif kiri dianggap sebagai situasi bermasalah bagi pengurai top-down. Pengurai top-down mulai mem-parsing dari simbol Start, yang dengan sendirinya merupakan non-terminal. Jadi, ketika parser menemukan non-terminal yang sama dalam turunannya, akan sulit untuk menilai kapan harus berhenti mengurai non-terminal kiri dan itu masuk ke loop tak terbatas.

Example:

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1) adalah contoh rekursi kiri langsung, di mana A adalah simbol non-terminal dan α mewakili string non-terminal.

(2) adalah contoh rekursi kiri tidak langsung.

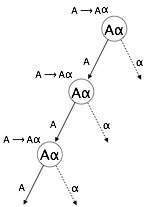
Parser top-down pertama-tama akan mengurai A, yang pada gilirannya akan menghasilkan string yang terdiri dari A itu sendiri dan parser dapat terus berputar selamanya.

Penghapusan Rekursi Kiri

Salah satu cara untuk menghilangkan rekursi kiri adalah dengan menggunakan teknik berikut:

Produksi

A => Aα | β

diubah menjadi produksi berikut

A => βA'
A'=> αA' | ε

Ini tidak memengaruhi string yang diturunkan dari tata bahasa, tetapi menghapus rekursi kiri langsung.

Metode kedua adalah dengan menggunakan algoritma berikut, yang seharusnya menghilangkan semua rekursi kiri langsung dan tidak langsung.

START

Arrange non-terminals in some order like A1, A2, A3,…, A_n

   for each i from 1 to n
      {
      for each j from 1 to i-1
         {
         replace each production of form A_i ⟹Aj
         with A_i ⟹ δ1  | δ2 | δ3 |…|  
         where A_j ⟹ δ₁ | δ₂|…| δ_n  are current A_j productions
         }
      }
   eliminate immediate left-recursion
   
END

Example

Set produksi

S => Aα | β 
A => Sd

setelah menerapkan algoritma di atas, seharusnya menjadi

S => Aα | β 
A => Aαd | βd

dan kemudian, segera hapus rekursi kiri menggunakan teknik pertama.

A  => βdA'
A' => αdA' | ε

Sekarang tidak ada produksi yang memiliki rekursi kiri langsung atau tidak langsung.

Anjak Kiri

Jika lebih dari satu aturan produksi tata bahasa memiliki string awalan yang sama, maka pengurai top-down tidak dapat membuat pilihan produksi mana yang harus dilakukan untuk mengurai string di tangan.

Example

Jika pengurai top-down menemui produksi seperti

A ⟹ αβ | α | …

Kemudian tidak dapat menentukan produksi mana yang akan diikuti untuk mengurai string karena kedua produksi dimulai dari terminal yang sama (atau non-terminal). Untuk menghilangkan kebingungan ini, kami menggunakan teknik yang disebut pemfaktoran kiri.

Pemfaktoran kiri mengubah tata bahasa agar berguna untuk pengurai top-down. Dalam teknik ini, kami membuat satu produksi untuk setiap prefiks umum dan sisa turunannya ditambahkan dengan produksi baru.

Example

Produksi di atas dapat ditulis sebagai

A => αA'
A'=> β |  | …

Sekarang parser hanya memiliki satu produksi per prefiks yang membuatnya lebih mudah untuk mengambil keputusan.

Set Pertama dan Ikuti

Bagian penting dari konstruksi tabel parser adalah membuat set pertama dan ikuti. Set ini dapat memberikan posisi sebenarnya dari terminal mana pun dalam derivasi. Hal ini dilakukan untuk membuat tabel parsing dimana keputusan untuk mengganti T [A, t] = α dengan beberapa aturan produksi.

Set Pertama

Himpunan ini dibuat untuk mengetahui simbol terminal apa yang diturunkan pada posisi pertama oleh non-terminal. Sebagai contoh,

α → t β

Artinya α menurunkan t (terminal) di posisi paling awal. Jadi, t ∈ PERTAMA (α).

Algoritma untuk menghitung Set pertama

Lihatlah definisi set FIRST (α):

jika α adalah terminal, maka PERTAMA (α) = {α}.
jika α adalah non-terminal dan α → ℇ adalah produksi, maka FIRST (α) = {ℇ}.
jika α adalah non-terminal dan α → 1 2 3… n dan setiap FIRST () berisi t maka t ada di FIRST (α).

Set pertama dapat dilihat sebagai:

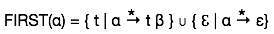
Ikuti Set

Demikian juga, kami menghitung simbol terminal apa yang segera mengikuti α non-terminal dalam aturan produksi. Kami tidak mempertimbangkan apa yang dapat dihasilkan oleh non-terminal tetapi sebaliknya, kami melihat apa yang akan menjadi simbol terminal berikutnya yang mengikuti produksi non-terminal.

Algoritma untuk menghitung set Ikuti:

jika α adalah simbol awal, maka IKUTI () = $
jika α adalah non-terminal dan memiliki produksi α → AB, maka FIRST (B) ada di FOLLOW (A) kecuali ℇ.
jika α non-terminal dan memiliki produksi α → AB, di mana B ℇ, maka IKUTI (A) di IKUTI (α).

Ikuti set dapat dilihat sebagai: IKUTI (α) = {t | S * αt *}

Batasan Penganalisis Sintaks

Penganalisis sintaks menerima masukan mereka, dalam bentuk token, dari penganalisis leksikal. Penganalisis leksikal bertanggung jawab atas validitas token yang disediakan oleh penganalisis sintaks. Penganalisis sintaks memiliki kelemahan berikut -

itu tidak dapat menentukan apakah token itu valid,
itu tidak dapat menentukan apakah token dideklarasikan sebelum digunakan,
itu tidak dapat menentukan apakah token diinisialisasi sebelum digunakan,
itu tidak dapat menentukan apakah operasi yang dilakukan pada tipe token valid atau tidak.

Tugas-tugas ini diselesaikan oleh penganalisis semantik, yang akan kita pelajari dalam Analisis Semantik.