Enkripsi Kunci Publik

Kriptografi Kunci Publik

Tidak seperti kriptografi kunci simetris, kami tidak menemukan penggunaan historis dari kriptografi kunci publik. Ini adalah konsep yang relatif baru.

Kriptografi simetris cocok untuk organisasi seperti pemerintah, militer, dan perusahaan keuangan besar yang terlibat dalam komunikasi rahasia.

Dengan penyebaran jaringan komputer yang lebih tidak aman dalam beberapa dekade terakhir, kebutuhan yang nyata untuk menggunakan kriptografi dalam skala yang lebih besar. Kunci simetris ternyata tidak praktis karena tantangan yang dihadapinya untuk manajemen kunci. Ini memunculkan kriptosistem kunci publik.

Proses enkripsi dan dekripsi digambarkan dalam ilustrasi berikut -

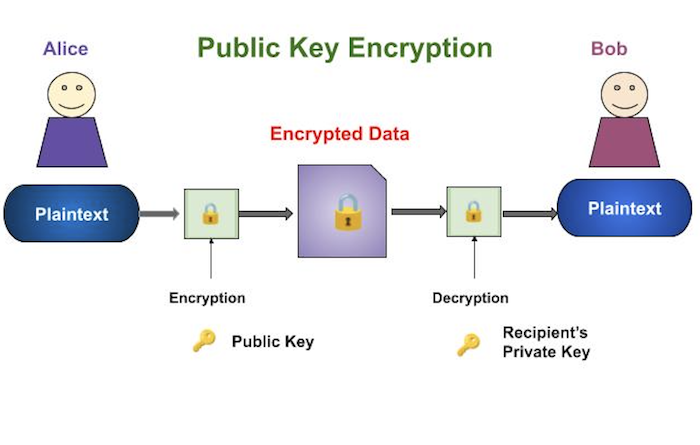
Properti terpenting dari skema enkripsi kunci publik adalah -

Kunci yang berbeda digunakan untuk enkripsi dan dekripsi. Ini adalah properti yang mengatur skema ini berbeda dari skema enkripsi simetris.
Setiap penerima memiliki kunci dekripsi unik, biasanya disebut sebagai kunci pribadinya.
Penerima perlu menerbitkan kunci enkripsi, yang disebut sebagai kunci publiknya.
Beberapa jaminan keaslian kunci publik diperlukan dalam skema ini untuk menghindari spoofing oleh musuh sebagai penerima. Umumnya, jenis kriptosistem ini melibatkan pihak ketiga tepercaya yang menyatakan bahwa kunci publik tertentu hanya dimiliki oleh orang atau entitas tertentu.
Algoritme enkripsi cukup kompleks untuk melarang penyerang menyimpulkan teks biasa dari teks tersandi dan kunci enkripsi (publik).
Meskipun kunci privat dan kunci publik terkait secara matematis, tidak mungkin untuk menghitung kunci privat dari kunci publik. Faktanya, bagian cerdas dari sistem kriptografi kunci publik mana pun adalah dalam merancang hubungan antara dua kunci.

Ada tiga jenis skema Enkripsi Kunci Publik. Kami membahasnya di bagian berikut -

Sistem Kriptografi RSA

Sistem kriptografi ini adalah salah satu sistem awal. Itu tetap menjadi cryptosystem yang paling banyak digunakan bahkan sampai hari ini. Sistem itu ditemukan oleh tiga orang sarjanaRon Rivest, Adi Shamir, dan Len Adleman dan karenanya, ini disebut sebagai sistem kriptografi RSA.

Kita akan melihat dua aspek dari sistem kriptografi RSA, generasi pertama dari pasangan kunci dan kedua algoritma dekripsi-enkripsi.

Pembuatan Pasangan Kunci RSA

Setiap orang atau pihak yang ingin berpartisipasi dalam komunikasi menggunakan enkripsi perlu menghasilkan sepasang kunci, yaitu kunci publik dan kunci privat. Proses yang diikuti dalam pembuatan kunci dijelaskan di bawah ini -

Generate the RSA modulus (n)
- Pilih dua bilangan prima besar, p dan q.
- Hitung n = p * q. Untuk enkripsi kuat yang tidak bisa dipecahkan, misalkan n menjadi angka besar, biasanya minimal 512 bit.
Find Derived Number (e)
- Jumlah e harus lebih besar dari 1 dan kurang dari (p - 1) (q - 1).
- Tidak boleh ada faktor persekutuan untuk e dan (p - 1) (q - 1) kecuali untuk 1. Dengan kata lain, dua bilangan e dan (p - 1) (q - 1) adalah coprime.
Form the public key
- Sepasang angka (n, e) membentuk kunci publik RSA dan dijadikan publik.
- Menariknya, meskipun n adalah bagian dari kunci publik, kesulitan dalam memfaktorkan bilangan prima besar memastikan bahwa penyerang tidak dapat menemukan dua bilangan prima (p & q) yang digunakan untuk mendapatkan n dalam waktu yang terbatas. Inilah kekuatan RSA.
Generate the private key
- Private Key d dihitung dari p, q, dan e. Untuk n dan e yang diberikan, ada bilangan unik d.
- Angka d adalah kebalikan dari e modulo (p - 1) (q - 1). Artinya d bilangan kurang dari (p - 1) (q - 1) sehingga bila dikalikan dengan e sama dengan 1 modulo (p - 1) (q - 1).
- Hubungan ini ditulis secara matematis sebagai berikut -

ed = 1 mod (p − 1)(q − 1)

Algoritma Extended Euclidean mengambil p, q, dan e sebagai masukan dan memberikan d sebagai keluaran.

Contoh

Contoh menghasilkan pasangan Kunci RSA diberikan di bawah ini. (Untuk memudahkan pemahaman, p & q bilangan prima yang diambil di sini adalah nilai kecil. Secara praktis, nilai tersebut sangat tinggi).

Misalkan dua bilangan prima menjadi p = 7 dan q = 13. Jadi, modulus n = pq = 7 x 13 = 91.
Pilih e = 5, yang merupakan pilihan yang valid karena tidak ada bilangan yang merupakan faktor persekutuan dari 5 dan (p - 1) (q - 1) = 6 × 12 = 72, kecuali 1.
Sepasang angka (n, e) = (91, 5) membentuk kunci publik dan dapat tersedia bagi siapa saja yang kami ingin dapat mengirimkan pesan terenkripsi kepada kami.
Masukkan p = 7, q = 13, dan e = 5 ke dalam Algoritma Euclidean yang Diperluas. Outputnya akan menjadi d = 29.
Periksa apakah d yang dihitung benar dengan menghitung -

de = 29 × 5 = 145 = 1 mod 72

Oleh karena itu, kunci publik adalah (91, 5) dan kunci privat adalah (91, 29).

Enkripsi dan Dekripsi

Setelah pasangan kunci dibuat, proses enkripsi dan dekripsi relatif langsung dan mudah secara komputasi.

Menariknya, RSA tidak langsung beroperasi pada string bit seperti dalam kasus enkripsi kunci simetris. Ini beroperasi pada nomor modulo n. Oleh karena itu, plaintext harus direpresentasikan sebagai rangkaian angka yang kurang dari n.

Enkripsi RSA

Misalkan pengirim ingin mengirim beberapa pesan teks ke seseorang yang kunci publiknya adalah (n, e).
Pengirim kemudian merepresentasikan teks biasa sebagai rangkaian angka yang kurang dari n.
Untuk mengenkripsi P teks biasa pertama, yaitu bilangan modulo n. Proses enkripsi adalah langkah matematis sederhana sebagai -

C = P^e mod n

Dengan kata lain ciphertext C sama dengan plaintext P dikalikan dengan e kali dan kemudian modulo n direduksi. Artinya C juga merupakan bilangan kurang dari n.
Kembali ke contoh Key Generation kami dengan plaintext P = 10, kami mendapatkan ciphertext C -

C = 10⁵ mod 91

Dekripsi RSA

Proses dekripsi untuk RSA juga sangat mudah. Misalkan penerima pasangan kunci publik (n, e) telah menerima ciphertext C.
Penerima menaikkan nilai C ke kekuatan kunci pribadinya d. Hasil modulo n akan menjadi teks biasa P.

Plaintext = C^d mod n

Kembali lagi ke contoh numerik kita, ciphertext C = 82 akan didekripsi ke nomor 10 menggunakan kunci pribadi 29 -

Plaintext = 82²⁹ mod 91 = 10

Analisis RSA

Keamanan RSA bergantung pada kekuatan dua fungsi terpisah. Kriptosistem RSA adalah kekuatan kriptosistem kunci publik paling populer yang didasarkan pada kesulitan praktis dalam memfaktorkan bilangan yang sangat besar.

Encryption Function - Ini dianggap sebagai fungsi satu arah untuk mengubah teks biasa menjadi teks tersandi dan dapat dibalik hanya dengan pengetahuan tentang kunci pribadi d.
Key Generation- Kesulitan menentukan kunci privat dari kunci publik RSA sama dengan memfaktorkan modulus n. Penyerang dengan demikian tidak dapat menggunakan pengetahuan tentang kunci publik RSA untuk menentukan kunci pribadi RSA kecuali dia dapat memfaktorkan n. Ini juga merupakan fungsi satu arah, beralih dari nilai p & q ke modulus n itu mudah tetapi kebalikannya tidak mungkin.

Jika salah satu dari kedua fungsi ini terbukti bukan satu arah, maka RSA akan rusak. Padahal, jika teknik anjak piutang dikembangkan secara efisien maka RSA tidak akan aman lagi.

Kekuatan enkripsi RSA turun drastis terhadap serangan jika bilangan p dan q bukan bilangan prima besar dan / atau kunci publik yang dipilih e adalah bilangan kecil.

Sistem Kriptografi ElGamal

Seiring dengan RSA, ada sistem kriptografi kunci publik lain yang diusulkan. Banyak dari mereka didasarkan pada versi berbeda dari Masalah Logaritma Diskrit.

Sistem kriptografi ElGamal, yang disebut Varian Kurva Eliptik, didasarkan pada Masalah Logaritma Diskrit. Ini memperoleh kekuatan dari asumsi bahwa logaritma diskrit tidak dapat ditemukan dalam kerangka waktu praktis untuk bilangan tertentu, sedangkan operasi kebalikan dari daya dapat dihitung secara efisien.

Mari kita lihat versi sederhana ElGamal yang bekerja dengan nomor modulo p. Dalam kasus varian kurva elips, ini didasarkan pada sistem angka yang sangat berbeda.

Generasi Pasangan Kunci ElGamal

Setiap pengguna kriptosistem ElGamal menghasilkan pasangan kunci melalui cara berikut -

Choosing a large prime p. Umumnya bilangan prima dengan panjang 1024 hingga 2048 bit dipilih.
Choosing a generator element g.
- Angka ini harus antara 1 dan p - 1, tetapi tidak boleh angka apa pun.
- Ini adalah generator dari kelompok perkalian bilangan bulat modulo p. Ini berarti untuk setiap bilangan bulat m co-prime ke p, ada bilangan bulat k sehingga g ^k = a mod n.
  
  Misalnya, 3 adalah generator dari grup 5 (Z ₅ = {1, 2, 3, 4}).

N	3 ⁿ	3 ⁿ mod 5
1	3	3
2	9	4
3	27	2
4	81	1

Choosing the private key. Kunci pribadi x adalah angka yang lebih besar dari 1 dan lebih kecil dari p − 1.
Computing part of the public key. Nilai y dihitung dari parameter p, g dan kunci pribadi x sebagai berikut -

y = g^x mod p

Obtaining Public key. Kunci publik ElGamal terdiri dari tiga parameter (p, g, y).

Sebagai contoh, anggaplah p = 17 dan g = 6 (Dapat dipastikan bahwa 6 adalah generator dari golongan Z ₁₇ ). Kunci pribadi x dapat berupa angka apa saja yang lebih besar dari 1 dan lebih kecil dari 71, jadi kita memilih x = 5. Nilai y kemudian dihitung sebagai berikut -

y = 6⁵ mod 17 = 7

Jadi kunci privatnya adalah 62 dan kunci publiknya adalah (17, 6, 7).

Enkripsi dan Dekripsi

Pembuatan pasangan kunci ElGamal secara komparatif lebih sederhana daripada proses yang setara untuk RSA. Tetapi enkripsi dan dekripsi sedikit lebih kompleks daripada RSA.

Enkripsi ElGamal

Misalkan pengirim ingin mengirim teks biasa ke seseorang yang kunci publik ElGamal-nya adalah (p, g, y), lalu -

Pengirim merepresentasikan teks biasa sebagai rangkaian angka modulo p.
Untuk mengenkripsi P teks biasa pertama, yang direpresentasikan sebagai nomor modulo p. Proses enkripsi untuk mendapatkan ciphertext C adalah sebagai berikut -
- Buat angka k secara acak;
- Hitung dua nilai C1 dan C2, di mana -

C1 = g^k mod p
C2 = (P^*y^k) mod p

Kirim ciphertext C, yang terdiri dari dua nilai terpisah (C1, C2), dikirim bersama.
Mengacu pada contoh pembuatan kunci ElGamal yang diberikan di atas, teks biasa P = 13 dienkripsi sebagai berikut -
- Buat angka secara acak, katakan k = 10
- Hitung dua nilai C1 dan C2, di mana -

C1 = 6¹⁰ mod 17
C2 = (13^*7¹⁰) mod 17 = 9

Kirim ciphertext C = (C1, C2) = (15, 9).

Dekripsi ElGamal

Untuk mendekripsi ciphertext (C1, C2) menggunakan kunci pribadi x, dua langkah berikut diambil -
- Hitung invers modular (C1) ^x modulo p, yaitu (C1) ^-x , biasanya disebut sebagai faktor dekripsi.
- Dapatkan teks biasa dengan menggunakan rumus berikut -

C2 × (C1)^-x mod p = Plaintext

Dalam contoh kami, untuk mendekripsi ciphertext C = (C1, C2) = (15, 9) menggunakan kunci pribadi x = 5, faktor dekripsinya adalah

15^-5 mod 17 = 9

Ekstrak teks biasa P = (9 × 9) mod 17 = 13.

Analisis ElGamal

Dalam sistem ElGamal, setiap pengguna memiliki kunci pribadi x. dan memilikithree components dari kunci publik - prime modulus p, generator g, and public Y = g^x mod p. Kekuatan ElGamal didasarkan pada kesulitan masalah logaritma diskrit.

Ukuran kunci aman umumnya> 1024 bit. Hari ini bahkan kunci panjang 2048 bit digunakan. Di depan kecepatan pemrosesan, Elgamal cukup lambat, ini digunakan terutama untuk protokol otentikasi kunci. Karena efisiensi pemrosesan yang lebih tinggi, varian Elliptic Curve dari ElGamal menjadi semakin populer.

Kriptografi Kurva Eliptik (ECC)

Elliptic Curve Cryptography (ECC) adalah istilah yang digunakan untuk menggambarkan rangkaian alat dan protokol kriptografi yang keamanannya didasarkan pada versi khusus dari masalah logaritma diskrit. Itu tidak menggunakan nomor modulo p.

ECC didasarkan pada kumpulan angka yang terkait dengan objek matematika yang disebut kurva elips. Ada aturan untuk menjumlahkan dan menghitung kelipatan dari bilangan ini, seperti halnya bilangan modulo p.

ECC menyertakan varian dari banyak skema kriptografi yang awalnya dirancang untuk nomor modular seperti enkripsi ElGamal dan Algoritma Tanda Tangan Digital.

Dipercaya bahwa masalah logaritma diskrit jauh lebih sulit bila diterapkan pada titik-titik pada kurva elips. Ini meminta peralihan dari bilangan modulo p ke titik-titik pada kurva elips. Juga tingkat keamanan yang setara dapat diperoleh dengan kunci yang lebih pendek jika kita menggunakan varian berbasis kurva eliptik.

Kunci yang lebih pendek menghasilkan dua manfaat -

Kemudahan manajemen kunci
Perhitungan yang efisien

Manfaat ini membuat varian skema enkripsi berbasis kurva elips sangat menarik untuk aplikasi di mana sumber daya komputasi dibatasi.

Skema RSA dan ElGamal - Perbandingan

Mari kita bandingkan secara singkat skema RSA dan ElGamal pada berbagai aspek.

RSA	ElGamal
Ini lebih efisien untuk enkripsi.	Ini lebih efisien untuk dekripsi.
Ini kurang efisien untuk dekripsi.	Ini lebih efisien untuk dekripsi.
Untuk tingkat keamanan tertentu, kunci yang panjang diperlukan di RSA.	Untuk tingkat keamanan yang sama, diperlukan kunci yang sangat pendek.
Ini diterima secara luas dan digunakan.	Ini baru dan tidak terlalu populer di pasar.