Sirkuit Elektronik - Penyearah
Setiap kali ada kebutuhan untuk mengubah daya AC ke DC, rangkaian penyearah datang untuk menyelamatkan. Dioda persimpangan PN sederhana bertindak sebagai penyearah. Kondisi bias maju dan bias balik dari dioda membuat perbaikan.
Pembetulan
Arus bolak-balik memiliki properti untuk mengubah statusnya secara terus menerus. Hal ini dipahami dengan mengamati gelombang sinus yang menunjukkan arus bolak-balik. Ini meningkatkan ke arah positif menuju ke nilai positif puncak, mengurangi dari sana ke normal dan kembali ke bagian negatif dan mencapai puncak negatif dan kembali ke normal dan melanjutkan.
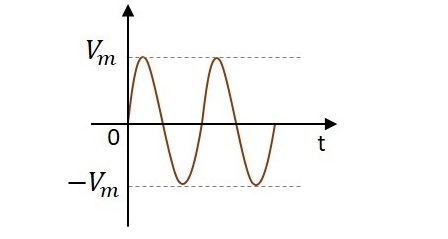
Selama perjalanannya dalam pembentukan gelombang, kita dapat mengamati bahwa gelombang tersebut bergerak ke arah positif dan negatif. Sebenarnya itu berubah sepenuhnya dan karenanya namanya arus bolak-balik.
Namun pada saat proses perbaikan arus bolak-balik ini diubah menjadi arus searah DC. Gelombang yang mengalir ke arah positif dan negatif sampai saat itu, akan mendapatkan arahnya terbatas hanya pada arah positif, bila diubah ke DC. Karenanya arus dibiarkan mengalir hanya ke arah positif dan ditolak ke arah negatif, seperti pada gambar di bawah ini.

Sirkuit yang melakukan rektifikasi disebut sebagai a Rectifier circuit. Dioda digunakan sebagai penyearah, untuk membangun rangkaian penyearah.
Jenis sirkuit penyearah
Ada dua jenis utama rangkaian penyearah, tergantung pada keluarannya. Mereka
- Penyearah Setengah Gelombang
- Penyearah Gelombang Penuh
Rangkaian penyearah setengah gelombang memperbaiki hanya setengah siklus positif dari suplai input sedangkan rangkaian penyearah gelombang penuh memperbaiki setengah siklus positif dan negatif dari suplai input.
Penyearah Setengah Gelombang
Nama penyearah setengah gelombang itu sendiri menyatakan bahwa rectification dilakukan hanya untuk halfdari siklus tersebut. Sinyal AC diberikan melalui trafo masukan yang naik atau turun sesuai dengan penggunaan. Sebagian besar trafo step down digunakan di rangkaian penyearah, sehingga dapat mengurangi tegangan input.
Sinyal input yang diberikan ke transformator dilewatkan melalui dioda PN-junction yang bertindak sebagai penyearah. Dioda ini mengubah tegangan AC menjadi dc berdenyut hanya untuk setengah siklus positif dari input. Sebuah resistor beban dihubungkan di ujung rangkaian. Gambar di bawah ini menunjukkan rangkaian penyearah setengah gelombang.
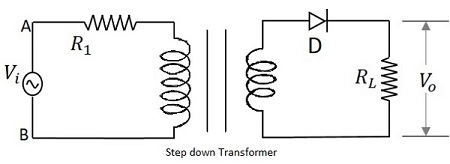
Bekerja dari HWR
TSinyal input diberikan ke trafo yang mengurangi level tegangan. Output dari transformator diberikan ke dioda yang berfungsi sebagai penyearah. Dioda ini ON (melakukan) untuk setengah siklus positif dari sinyal input. Karenanya arus mengalir di sirkuit dan akan ada penurunan tegangan melintasi resistor beban. Dioda akan OFF (tidak bekerja) untuk setengah siklus negatif dan karenanya keluaran untuk setengah siklus negatif adalah, $ i_ {D} = 0 $ dan $ V_ {o} = 0 $.
Oleh karena itu, keluarannya hanya untuk setengah siklus positif dari tegangan masukan saja (mengabaikan arus bocor terbalik). Output ini akan berdenyut yang dibawa melintasi resistor beban.
Bentuk gelombang dari HWR
Bentuk gelombang input dan output seperti yang ditunjukkan pada gambar berikut.
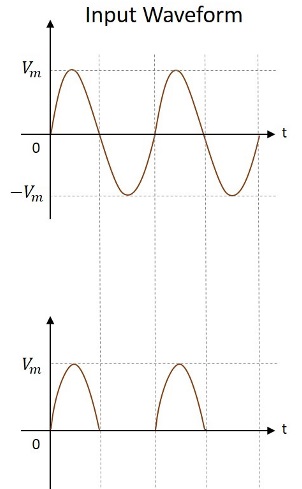
Oleh karena itu, keluaran dari penyearah setengah gelombang adalah dc yang berdenyut. Mari kita coba menganalisis rangkaian di atas dengan memahami beberapa nilai yang diperoleh dari output penyearah setengah gelombang.
Analisis Penyearah Setengah Gelombang
Untuk menganalisis rangkaian penyearah setengah gelombang, mari kita pertimbangkan persamaan tegangan input.
$$ v_ {i} = V_ {m} \ sin \ omega t $$
$ V_ {m} $ adalah nilai maksimum tegangan suplai.
Mari kita asumsikan bahwa dioda itu ideal.
- Hambatan dalam arah maju, yaitu dalam keadaan ON adalah $ R_f $.
- Hambatan dalam arah sebaliknya, yaitu dalam keadaan OFF adalah $ R_r $.
Sekarang i di dioda atau resistor beban $ R_L $ diberikan oleh
$ i = I_m \ sin \ omega t \ quad untuk \ quad 0 \ leq \ omega t \ leq 2 \ pi $
$ i = 0 \ quad \ quad \ quad \ quad untuk \ quad \ pi \ leq \ omega t \ leq 2 \ pi $
Dimana
$$ I_m = \ frac {V_m} {R_f + R_L} $$
Arus Keluaran DC
Rata-rata $ I_ {dc} $ saat ini diberikan oleh
$$ I_ {dc} = \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i \: d \ left (\ omega t \ right) $$
$$ = \ frac {1} {2 \ pi} \ kiri [\ int_ {0} ^ {\ pi} I_m \ sin \ omega t \: d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0 \: d \ left (\ omega t \ right) \ right] $$
$$ = \ frac {1} {2 \ pi} \ kiri [I_m \ kiri \ {- \ cos \ omega t \ kanan \} _ {0} ^ {\ pi} \ kanan] $$
$$ = \ frac {1} {2 \ pi} \ kiri [I_m \ kiri \ {+ 1- \ kiri (-1 \ kanan) \ kanan \} \ kanan] = \ frac {I_m} {\ pi} = 0,318 I_m $$
Mengganti nilai $ I_m $, kita dapatkan
$$ I_ {dc} = \ frac {V_m} {\ pi \ kiri (R_f + R_L \ kanan)} $$
Jika $ R_L >> R_f $, maka
$$ I_ {dc} = \ frac {V_m} {\ pi R_L} = 0,318 \ frac {V_m} {R_L} $$
Tegangan Output DC
Tegangan keluaran DC diberikan oleh
$$ V_ {dc} = I_ {dc} \ times R_L = \ frac {I_m} {\ pi} \ times R_L $$
$$ = \ frac {V_m \ times R_L} {\ pi \ kiri (R_f + R_L \ kanan)} = \ frac {V_m} {\ pi \ kiri \ {1+ \ kiri (R_f / R_L \ kanan) \ kanan \}} $$
Jika $ R_L >> R_f $, maka
$$ V_ {dc} = \ frac {V_m} {\ pi} = 0,318 V_m $$
Arus dan Tegangan RMS
Nilai arus RMS diberikan oleh
$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i ^ {2} d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$
$$ I_ {rms} = \ kiri [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} I_ {m} ^ {2} \ sin ^ {2} \ omega t \: d \ left (\ omega t \ right) + \ frac {1} {2 \ pi} \ int _ {\ pi} ^ {2 \ pi} 0 \: d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$
$$ = \ kiri [\ frac {I_ {m} ^ {2}} {2 \ pi} \ int_ {0} ^ {\ pi} \ kiri (\ frac {1- \ cos 2 \ omega t} {2 } \ kanan) d \ kiri (\ omega t \ kanan) \ kanan] ^ {\ frac {1} {2}} $$
$$ = \ kiri [\ frac {I_ {m} ^ {2}} {4 \ pi} \ kiri \ {\ kiri (\ omega t \ kanan) - \ frac {\ sin 2 \ omega t} {2} \ kanan \} _ {0} ^ {\ pi} \ kanan] ^ {\ frac {1} {2}} $$
$$ = \ kiri [\ frac {I_ {m} ^ {2}} {4 \ pi} \ kiri \ {\ pi - 0 - \ frac {\ sin 2 \ pi} {2} + \ sin 0 \ kanan \} \ kanan] ^ {\ frac {1} {2}} $$
$$ = \ kiri [\ frac {I_ {m} ^ {2}} {4 \ pi} \ kanan] ^ {\ frac {1} {2}} = \ frac {I_m} {2} $$
$$ = \ frac {V_m} {2 \ kiri (R_f + R_L \ kanan)} $$
Tegangan RMS yang melintasi beban adalah
$$ V_ {rms} = I_ {rms} \ times R_L = \ frac {V_m \ times R_L} {2 \ left (R_f + R_L \ right)} $$
$$ = \ frac {V_m} {2 \ kiri \ {1+ \ kiri (R_f / R_L \ kanan) \ kanan \}} $$
Jika $ R_L >> R_f $, maka
$$ V_ {rms} = \ frac {V_m} {2} $$
Efisiensi Penyearah
Sirkuit apa pun harus efisien dalam bekerja untuk hasil yang lebih baik. Untuk menghitung efisiensi penyearah setengah gelombang, rasio daya keluaran terhadap daya masukan harus dipertimbangkan.
Efisiensi penyearah didefinisikan sebagai
$$ \ eta = \ frac {dcpower \: \: dikirim \: \: ke \: \: the \: \: load} {acinput \: \: power \: \: from \: \: transformer \: \ : sekunder} = \ frac {P_ {ac}} {P_ {dc}} $$
Sekarang
$$ P_ {dc} = \ kiri ({I_ {dc}} \ kanan) ^ 2 \ times R_L = \ frac {I_m R_L} {\ pi ^ 2} $$
Lebih lanjut
$$ P_ {ac} = P_a + P_r $$
Dimana
$ P_a = daya \: dihilangkan \: di \: persimpangan \: \: dari \: dioda $
$$ = I_ {rms} ^ {2} \ times R_f = \ frac {I_ {m} ^ {2}} {4} \ times R_f $$
Dan
$$ P_r = power \: dihamburkan \: di \: the \: load \: resistance $$
$$ = I_ {rms} ^ {2} \ times R_L = \ frac {I_ {m} ^ {2}} {4} \ times R_L $$
$$ P_ {ac} = \ frac {I_ {m} ^ {2}} {4} \ times R_f + \ frac {I_ {m} ^ {2}} {4} \ times R_L = \ frac {I_ {m } ^ {2}} {4} \ kiri (R_f + R_L \ kanan) $$
Dari kedua ekspresi $ P_ {ac} $ dan $ P_ {dc} $, kita dapat menulis
$$ \ eta = \ frac {I_ {m} ^ {2} R_L / \ pi ^ 2} {I_ {m} ^ {2} \ kiri (R_f + R_L \ kanan) / 4} = \ frac {4} {\ pi ^ 2} \ frac {R_L} {\ kiri (R_f + R_L \ kanan)} $$
$$ = \ frac {4} {\ pi ^ 2} \ frac {1} {\ kiri \ {1+ \ kiri (R_f / R_L \ kanan) \ kanan \}} = \ frac {0,406} {\ kiri \ {1+ \ kiri (R_f / R_L \ kanan) \ kanan \}} $$
Persentase efisiensi penyearah
$$ \ eta = \ frac {40.6} {\ lbrace1 + \ lgroup \: R_ {f} / R_ {L} \ rgroup \ rbrace} $$
Secara teoritis, nilai maksimum efisiensi penyearah setengah gelombang penyearah adalah 40,6% ketika $ R_ {f} / R_ {L} = 0 $
Selanjutnya, efisiensi dapat dihitung dengan cara berikut
$$ \ eta = \ frac {P_ {dc}} {P_ {ac}} = \ frac {\ kiri (I_ {dc} \ kanan) ^ 2R_L} {\ kiri (I_ {rms} \ kanan) ^ 2R_L} = \ frac {\ kiri (V_ {dc} / R_L \ kanan) ^ 2R_L} {\ kiri (V_ {rms} / R_L \ kanan) ^ 2R_L} = \ frac {\ kiri (V_ {dc} \ kanan) ^ 2} {\ kiri (V_ {rms} \ kanan) ^ 2} $$
$$ = \ frac {\ kiri (V_m / \ pi \ kanan) ^ 2} {\ kiri (V_m / 2 \ kanan) ^ 2} = \ frac {4} {\ pi ^ 2} = 0,406 $$
$$ = 40.6 \% $$
Faktor Riak
Keluaran yang diperbaiki berisi sejumlah komponen AC yang ada di dalamnya, dalam bentuk riak. Ini dipahami dengan mengamati bentuk gelombang keluaran dari penyearah setengah gelombang. Untuk mendapatkan dc murni, kita perlu memiliki gambaran tentang komponen ini.
Faktor riak memberikan gelombang keluaran yang diperbaiki. Ini dilambangkan dengany. Ini dapat didefinisikan sebagai rasio nilai efektif komponen ac tegangan atau arus terhadap nilai langsung atau nilai rata-rata.
$$ \ gamma = \ frac {riak \: voltase} {dc \: voltase} = \ frac {rms \: nilai \: dari \: menyertai} {nilai dc \: dari \: gelombang} = \ frac {\ kiri ( V_r \ kanan) _ {rms}} {v_ {dc}} $$
Sini,
$$ \ kiri (V_r \ kanan) _ {rms} = \ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}} $$
Karena itu,
$$ \ gamma = \ frac {\ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}}} {V_ {dc}} = \ sqrt {\ left (\ frac {V_ {rms} } {V_ {dc}} \ kanan) ^ 2-1} $$
Sekarang,
$$ V_ {rms} = \ kiri [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} V_ {m} ^ {2} \ sin ^ 2 \ omega t \: d \ kiri (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$
$$ = V_m \ kiri [\ frac {1} {4 \ pi} \ int_ {0} ^ {\ pi} \ kiri (1- \ cos2 \: \ omega t \ kanan) d \ kiri (\ omega t \ kanan) \ kanan] ^ {\ frac {1} {2}} = \ frac {V_m} {2} $$
$$ V_ {dc} = V_ {av} = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} V_m \ sin \ omega t \: d \ left (\ omega t \ kanan) + \ int_ {0} ^ {2 \ pi} 0.d \ kiri (\ omega t \ kanan) \ kanan] $$
$$ = \ frac {V_m} {2 \ pi} \ kiri [- \ cos \ omega t \ kanan] _ {0} ^ {\ pi} = \ frac {V_m} {\ pi} $$
$$ \ gamma = \ sqrt {\ kiri [\ kiri \ {\ frac {\ kiri (V_m / 2 \ kanan)} {\ kiri (V_m / \ pi \ kanan)} \ kanan \} ^ 2-1 \ kanan ]} = \ sqrt {\ left \ {\ left (\ frac {\ pi} {2} \ right) ^ 2-1 \ right \}} = 1,21 $$
Faktor riak juga didefinisikan sebagai
$$ \ gamma = \ frac {\ kiri (I_r \ kanan) _ {rms}} {I_ {dc}} $$
Karena nilai faktor riak yang ada dalam penyearah setengah gelombang adalah 1,21, itu berarti jumlah ac yang ada dalam output adalah $ 121 \% $ dari tegangan dc
Peraturan
Arus yang melalui beban dapat bervariasi tergantung pada tahanan beban. Tetapi bahkan pada kondisi seperti itu, kami mengharapkan tegangan output kami yang dibawa melintasi resistor beban itu, menjadi konstan. Jadi, tegangan kita perlu diatur bahkan dalam kondisi beban yang berbeda.
Variasi tegangan keluaran DC dengan perubahan arus beban DC didefinisikan sebagai Regulation. Peraturan persentase dihitung sebagai berikut.
$$ Persentase \: regulasi = \ frac {V_ {no \: load} -V_ {full \: load}} {V_ {full \: load}} \ times 100 \% $$
Semakin rendah pengaturan persentase, semakin baik catu daya. Catu daya yang ideal akan memiliki regulasi persentase nol.
Faktor Pemanfaatan Transformator
Daya DC yang akan dikirim ke beban, dalam rangkaian penyearah menentukan peringkat transformator yang digunakan dalam suatu rangkaian.
Jadi, faktor pemanfaatan transformator didefinisikan sebagai
$$ TUF = \ frac {dcpower \: to \: be \: dikirim \: ke \: the \: load} {acrating \: of \: the \: transformer \: secondary} $$
$$ = \ frac {P_ {dc}} {P_ {ac \ left (dinilai \ kanan)}} $$
Menurut teori trafo, tegangan pengenal sekunder akan
$$ V_m / \ sqrt {2} $$
Tegangan RMS sebenarnya yang mengalir melaluinya
$$ I_m / 2 $$
Karena itu
$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left (V_m / \ sqrt {2} \ right) \ times \ left (I_m / 2 \ right)} $ $
Tapi
$$ V_m = I_m \ kiri (R_f + R_L \ kanan) $$
Karena itu
$$ TUF = \ frac {\ kiri (I_m / \ pi \ kanan) ^ 2 \ times R_L} {\ kiri \ {I_m \ kiri (R_f + R_L \ kanan) / \ sqrt {2} \ kanan \} \ kali \ kiri (I_m / 2 \ kanan)} $$
$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} \ times \ frac {R_L} {\ kiri (R_f + R_L \ kanan)} $$
$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} = 0,287 $$
Tegangan Terbalik Puncak
Dioda ketika dihubungkan dalam bias balik, harus dioperasikan di bawah level tegangan yang terkendali. Jika tegangan aman itu terlampaui, dioda akan rusak. Oleh karena itu sangat penting untuk mengetahui tentang tegangan maksimum itu.
Tegangan terbalik maksimum yang dapat ditahan dioda tanpa dihancurkan disebut sebagai Peak Inverse Voltage. Pendeknya,PIV.
Di sini PIV tidak lain adalah Vm
Faktor Bentuk
Ini dapat dipahami sebagai rata-rata matematis dari nilai absolut semua titik pada bentuk gelombang. Ituform factordidefinisikan sebagai rasio nilai RMS dengan nilai rata-rata. Ini dilambangkan denganF.
$$ F = \ frac {rms \: nilai} {rata-rata \: nilai} = \ frac {I_m / 2} {I_m / \ pi} = \ frac {0,5I_m} {0,318I_m} = 1,57 $$
Faktor Puncak
Nilai puncak riak harus dipertimbangkan untuk mengetahui seberapa efektif rektifikasi tersebut. Nilai faktor puncak juga menjadi pertimbangan penting.Peak factor didefinisikan sebagai rasio nilai puncak dengan nilai RMS.
Karena itu
$$ Faktor Puncak = \ frac {Puncak \: nilai} {rms \: nilai} = \ frac {V_m} {V_m / 2} = 2 $$
Semua ini adalah parameter penting yang harus dipertimbangkan saat mempelajari penyearah.