Fungsi Khusus LPF dan HPF
Sirkuit filter jalur rendah dan jalur tinggi digunakan sebagai sirkuit khusus dalam banyak aplikasi. Filter low-pass (LPF) dapat berfungsi sebagai fileIntegrator, sedangkan high-pass filter (HPF) dapat bekerja sebagai file Differentiator. Kedua fungsi matematika ini hanya mungkin dengan rangkaian ini yang mengurangi upaya seorang insinyur elektronik dalam banyak aplikasi.
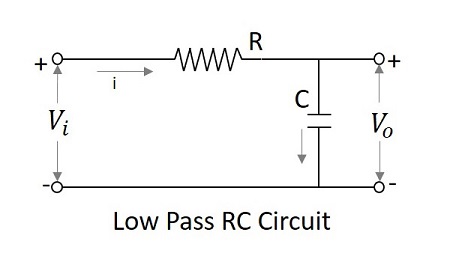
Filter Low Pass sebagai Integrator
Pada frekuensi rendah, reaktansi kapasitif cenderung menjadi tak terbatas dan pada frekuensi tinggi reaktansi menjadi nol. Oleh karena itu pada frekuensi rendah, LPF memiliki keluaran yang terbatas dan pada frekuensi tinggi keluarannya nihil, yang sama untuk rangkaian integrator. Oleh karena itu low pass filter dapat dikatakan bekerja sebagai sebuahintegrator.
Agar LPF berperilaku sebagai integrator
$$ \ tau \ gg T $$
Dimana $ \ tau = RC $ konstanta waktu rangkaian
Maka variasi tegangan pada C sangat kecil.
$$ V_ {i} = iR + \ frac {1} {C} \ int i \: dt $$
$$ V_ {i} \ cong iR $$
$$ Sejak \: \: \ frac {1} {C} \ int i \: dt \ ll iR $$
$$ i = \ frac {V_ {i}} {R} $$
$$ Sejak \: \: V_ {0} = \ frac {1} {C} \ int i dt = \ frac {1} {RC} \ int V_ {i} dt = \ frac {1} {\ tau} \ int V_ {i} dt $$
$$ Output \ propto \ int masukan $$
Oleh karena itu LPF dengan konstanta waktu yang besar menghasilkan keluaran yang sebanding dengan integral dari suatu masukan.
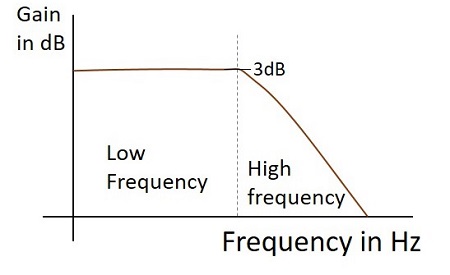
Respon Frekuensi
Respon frekuensi dari filter low pass praktis, ketika berfungsi sebagai Integrator adalah seperti yang ditunjukkan di bawah ini.
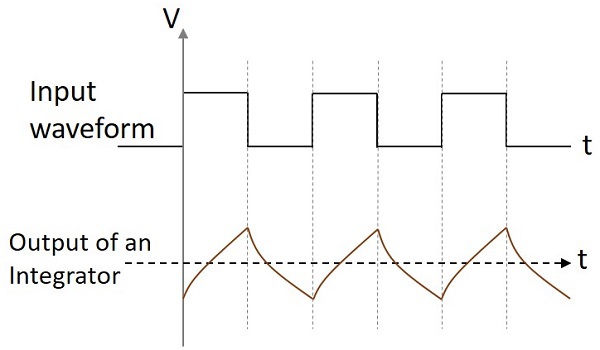
Bentuk Gelombang Keluaran
Jika rangkaian integrator diberi input gelombang sinus, outputnya adalah gelombang cosinus. Jika input berupa gelombang persegi maka bentuk gelombang output berubah bentuk dan muncul seperti pada gambar di bawah ini.
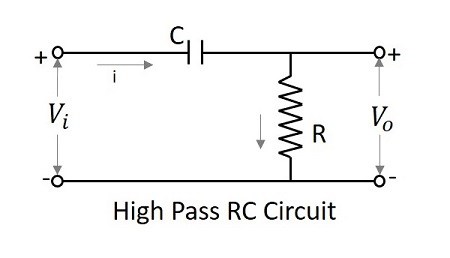
High Pass Filter sebagai Diferensiator
Pada frekuensi rendah, keluaran dari sebuah diferensiator adalah nol sedangkan pada frekuensi tinggi, keluarannya memiliki nilai yang terbatas. Ini sama dengan pembeda. Oleh karena itu, high pass filter dikatakan berperilaku sebagai pembeda.
Jika konstanta waktu RC HPF jauh lebih kecil dari periode waktu sinyal input, maka rangkaian berfungsi sebagai pembeda. Kemudian penurunan tegangan pada R sangat kecil jika dibandingkan dengan penurunan tegangan pada C.
$$ V_ {i} = \ frac {1} {C} \ int i \: dt + iR $$
Tapi $ iR = V_ {0} $ itu kecil
$$ sejak V_ {i} = \ frac {1} {C} \ int i \: dt $$
$$ i = \ frac {V_ {0}} {R} $$
$$ Sejak \: V_ {i} = \ frac {1} {\ tau} \ int V_ {0} \: dt $$
Dimana $ \ tau = RC $ konstanta waktu rangkaian.
Membedakan di kedua sisi,
$$ \ frac {dV_ {i}} {dt} = \ frac {V_0} {\ tau} $$
$$ V_ {0} = \ tau \ frac {dV_ {i}} {dt} $$
$$ Sejak \: V_ {0} \ propto \ frac {dV_ {i}} {dt} $$
Outputnya sebanding dengan perbedaan sinyal input.
Respon Frekuensi
Respon frekuensi dari filter high pass praktis, ketika berfungsi sebagai Diferensiator adalah seperti yang ditunjukkan di bawah ini.
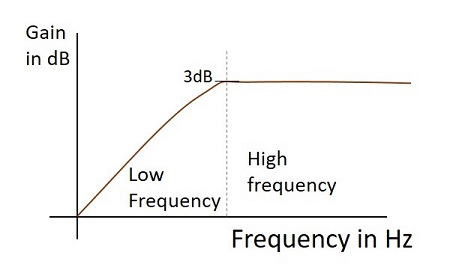
Bentuk Gelombang Keluaran
Jika rangkaian diferensiator diberi input gelombang sinus, outputnya adalah gelombang kosinus. Jika input berupa gelombang persegi maka bentuk gelombang output berubah bentuk dan muncul seperti pada gambar di bawah ini.
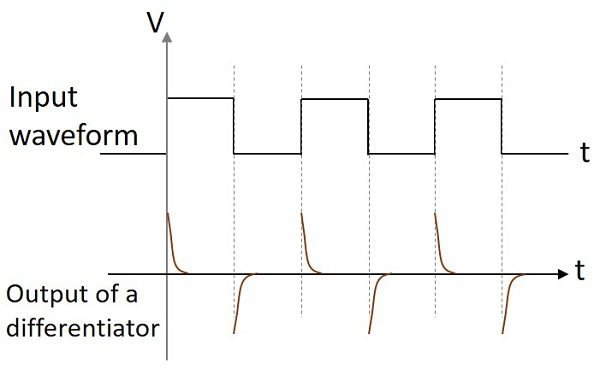
Kedua sirkuit ini banyak digunakan dalam berbagai aplikasi elektronik. Rangkaian diferensiator menghasilkan tegangan keluaran yang konstan ketika masukan yang diterapkan cenderung berubah secara konstan. Sirkuit integrator menghasilkan tegangan keluaran yang terus berubah ketika tegangan masukan yang diterapkan konstan.