Rekayasa Gelombang Mikro - Tee E-Plane
Sambungan E-Plane Tee dibentuk dengan memasang pandu gelombang sederhana ke dimensi yang lebih luas dari pandu gelombang persegi panjang, yang sudah memiliki dua port. Lengan pandu gelombang persegi panjang membuat dua port disebutcollinear ports yaitu Port1 dan Port2, sedangkan yang baru, Port3 disebut sebagai Side arm atau E-arm. Tee E-plane nya juga disebut sebagaiSeries Tee.
Karena sumbu lengan samping sejajar dengan medan listrik, sambungan ini disebut sambungan E-Plane Tee. Ini juga disebut sebagaiVoltage atau Series junction. Port 1 dan 2 berada di luar fase 180 ° satu sama lain. Detail penampang tee bidang-E dapat dipahami pada gambar berikut.
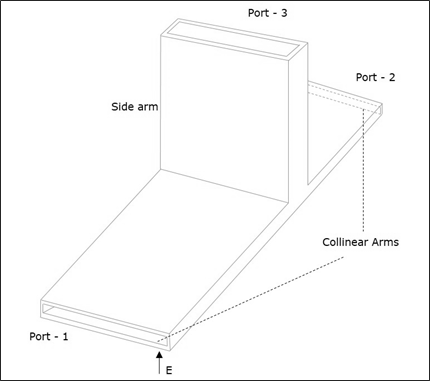
Gambar berikut menunjukkan koneksi yang dibuat oleh sidearm ke pandu gelombang dua arah untuk membentuk port paralel.
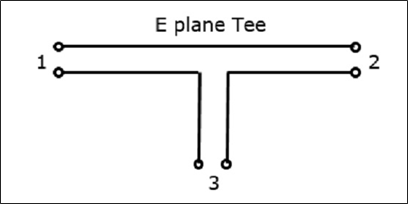
Properti E-Plane Tee
Properti E-Plane Tee dapat ditentukan oleh matriks $ [S] _ {3x3} $.
Ini adalah matriks 3 × 3 karena ada 3 kemungkinan masukan dan 3 kemungkinan keluaran.
$ [S] = \ mulai {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
Koefisien hamburan $ S_ {13} $ dan $ S_ {23} $ keluar dari fase sebesar 180 ° dengan masukan pada port 3.
$ S_ {23} = -S_ {13} $........ Equation 2
Pelabuhan sangat cocok dengan persimpangan.
$ S_ {33} = 0 $........ Equation 3
Dari sifat simetris,
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} \: \: S_ {13} = S_ {31} $........ Equation 4
Mempertimbangkan persamaan 3 & 4, matriks $ [S] $ dapat ditulis sebagai,
$ [S] = \ mulai {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} $........ Equation 5
Kita dapat mengatakan bahwa kita memiliki empat hal yang tidak diketahui, dengan mempertimbangkan properti simetrinya.
Dari properti Kesatuan
$$ [S] [S] \ ast = [I] $$
$$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & -S_ {13} ^ {*} \\ S_ {13} ^ {*} & -S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin { bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Mengalikan kita dapatkan,
(Memperhatikan R sebagai baris dan C sebagai kolom)
$ R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ kiri | S_ {11} \ kanan | ^ 2 + \ kiri | S_ {11} \ kanan | ^ 2 + \ kiri | S_ {11} \ kanan | ^ 2 = 1 $........ Equation 6
$ R_2C_2: \ kiri | S_ {12} \ kanan | ^ 2 + \ kiri | S_ {22} \ kanan | ^ 2 + \ kiri | S_ {13} \ kanan | ^ 2 = 1 $......... Equation 7
$ R_3C_3: \ kiri | S_ {13} \ kanan | ^ 2 + \ kiri | S_ {13} \ kanan | ^ 2 = 1 $......... Equation 8
$ R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 1 $ ......... Equation 9
Menyamakan persamaan 6 & 7, kita dapatkan
$ S_ {11} = S_ {22} $ ......... Equation 10
Dari Persamaan 8,
$ 2 \ tersisa | S_ {13} \ right | ^ 2 \ quad atau \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 11
Dari Persamaan 9,
$ S_ {13} \ kiri (S_ {11} ^ {*} - S_ {12} ^ {*} \ kanan) $
Atau $ S_ {11} = S_ {12} = S_ {22} $ ......... Equation 12
Menggunakan persamaan 10, 11, dan 12 pada persamaan 6,
kita mendapatkan,
$ \ kiri | S_ {11} \ kanan | ^ 2 + \ kiri | S_ {11} \ kanan | ^ 2 + \ frac {1} {2} = 1 $
$ 2 \ tersisa | S_ {11} \ kanan | ^ 2 = \ frac {1} {2} $
Atau $ S_ {11} = \ frac {1} {2} $ ......... Equation 13
Mengganti nilai dari persamaan di atas dalam matriks $ [S] $,
Kita mendapatkan,
$$ \ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac { 1} {2} & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
Kita tahu bahwa $ [b] $ = $ [S] [a] $
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {2} & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2 }} & - \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
Ini adalah matriks hamburan untuk E-Plane Tee, yang menjelaskan sifat hamburannya.