Rekayasa Microwave - Perangkat Microwave

Sama seperti sistem lain, sistem gelombang mikro terdiri dari banyak komponen gelombang mikro, terutama dengan sumber di satu ujung dan beban di ujung lainnya, yang semuanya terhubung dengan pandu gelombang atau kabel koaksial atau sistem saluran transmisi.

Berikut adalah properti dari pandu gelombang.

SNR tinggi
Atenuasi rendah
Kehilangan penyisipan lebih rendah

Fungsi Gelombang Mikro Pandu Gelombang

Pertimbangkan sebuah pandu gelombang yang memiliki 4 port. Jika daya diterapkan ke satu port, ia melewati semua 3 port dalam beberapa proporsi di mana beberapa di antaranya mungkin mencerminkan kembali dari port yang sama. Konsep ini secara jelas digambarkan pada gambar berikut.

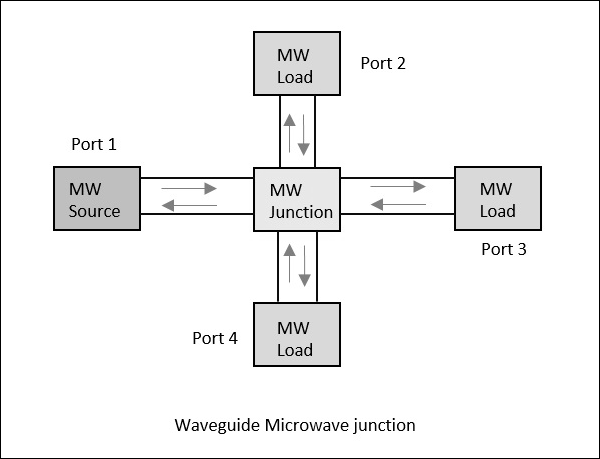
Parameter Hamburan

Untuk jaringan dua port, seperti yang ditunjukkan pada gambar berikut, jika daya diterapkan pada satu port, seperti yang baru saja kita diskusikan, sebagian besar daya keluar dari port lain, sementara beberapa di antaranya mencerminkan kembali ke port yang sama. Pada gambar berikut, jikaV₁ atau V₂ diterapkan, lalu I₁ atau I₂ arus mengalir masing-masing.

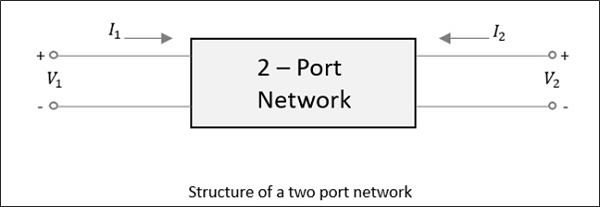
Jika sumber diterapkan ke port yang berlawanan, dua kombinasi lainnya akan dipertimbangkan. Jadi, untuk jaringan dua port, kombinasi 2 × 2 = 4 cenderung terjadi.

Gelombang perjalanan dengan kekuatan terkait ketika menyebar melalui port, persimpangan gelombang mikro dapat ditentukan oleh Parameter-S atau Scattering Parameters, yang direpresentasikan dalam bentuk matriks, yang disebut sebagai "Scattering Matrix".

Matriks Hamburan

Ini adalah matriks persegi yang memberikan semua kombinasi hubungan daya antara berbagai port input dan output dari sambungan gelombang mikro. Elemen-elemen matriks ini disebut"Scattering Coefficients" atau "Scattering (S) Parameters".

Perhatikan gambar berikut.

Di sini, sumber dihubungkan melalui $ i ^ {th} $ line sedangkan $ a_1 $ adalah gelombang insiden dan $ b_1 $ adalah gelombang yang dipantulkan.

Jika suatu relasi diberikan antara $ b_1 $ dan $ a_1 $,

$$ b_1 = (refleksi \: \: koefisien) a_1 = S_ {1i} a_1 $$

Dimana

$ S_ {1i} $ = Koefisien refleksi $ 1 ^ {st} $ line (dengan $ i $ adalah port input dan $ 1 $ adalah port output)
$ 1 $ = Refleksi dari $ 1 ^ {st} $ line
$ i $ = Sumber terhubung pada $ i ^ {th} $ baris

Jika impedansinya cocok, maka daya akan ditransfer ke beban. Tidak mungkin, jika impedansi beban tidak cocok dengan impedansi karakteristik. Kemudian refleksi terjadi. Artinya, refleksi terjadi jika

$$ Z_l \ neq Z_o $$

Namun, jika ketidakcocokan ini terjadi pada lebih dari satu port, misalnya $ 'n' $ ports, maka $ i = 1 $ hingga $ n $ (karena $ i $ dapat berupa baris apa pun dari $ 1 $ hingga $ n $).

Oleh karena itu, kami punya

$$ b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n $$

$$ b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n $$

$$. $$

$$ b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n $$

Ketika semuanya ini disimpan dalam bentuk matriks,

$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \\. \\. \\. \\ b_n \ end {bmatrix} = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13 } & ... & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & ... & S_ {2n} \\. &. &. & ... &. \\. &. &. & ... &. \\. &. &. & ... &. \\ S_ {n1} & S_ {n2} & S_ {n3} & ... & S_ {nn} \\ \ end {bmatrix} \ times \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \\. \ \. \\. \\ a_n \ end {bmatrix} $$

Column matrix $ [b] $ Scattering matrix $ [S] $Matrix $ [a] $

Matriks kolom $ \ left [b \ right] $ berhubungan dengan gelombang yang dipantulkan atau keluaran, sedangkan matriks $ \ left [a \ right] $ berhubungan dengan gelombang datang atau masukan. Matriks kolom hamburan $ \ left [s \ right] $ yang berurutan $ n \ times n $ berisi koefisien refleksi dan koefisien transmisi. Karena itu,

$$ \ kiri [b \ kanan] = \ kiri [S \ kanan] \ kiri [a \ kanan] $$

Properti Matriks [S]

Matriks hamburan diindikasikan sebagai matriks $ [S] $. Ada beberapa properti standar untuk matriks $ [S] $. Mereka adalah -

$ [S] $ selalu merupakan matriks orde kuadrat (nxn)

$ [S] _ {n \ kali n} $
$ [S] $ adalah matriks simetris

yaitu, $ S_ {ij} = S_ {ji} $
$ [S] $ adalah matriks kesatuan

yaitu, $ [S] [S] ^ * = I $
Jumlah produk dari setiap suku dari setiap baris atau kolom dikalikan dengan konjugasi kompleks dari suku terkait dari baris atau kolom lainnya adalah nol. yaitu,

$$ \ sum_ {i = j} ^ {n} S_ {ik} S_ {ik} ^ {*} = 0 \: untuk \: k \ neq j $$

$$ (k = 1,2,3, ... \: n) \: dan \: (j = 1,2,3, ... \: n) $$

Jika jarak listrik antara beberapa $ k ^ {th} $ port dan persimpangan adalah $ \ beta _kI_k $, maka koefisien $ S_ {ij} $ yang melibatkan $ k $, akan dikalikan dengan faktor $ e ^ {- j \ beta kIk} $

Dalam beberapa bab berikutnya, kita akan melihat berbagai jenis sambungan Microwave Tee.