Pemodelan & Simulasi - Panduan Cepat
Modellingadalah proses merepresentasikan model yang meliputi konstruksi dan pengerjaannya. Model ini mirip dengan sistem nyata, yang membantu analis memprediksi efek perubahan pada sistem. Dengan kata lain pemodelan adalah membuat model yang merepresentasikan suatu sistem beserta propertinya. Ini adalah tindakan membangun model.
Simulationsuatu sistem adalah pengoperasian model dalam hal waktu atau ruang, yang membantu menganalisis kinerja sistem yang ada atau yang diusulkan. Dengan kata lain, simulasi adalah proses menggunakan model untuk mempelajari kinerja suatu sistem. Ini adalah tindakan menggunakan model untuk simulasi.
Sejarah Simulasi
Perspektif sejarah simulasi seperti yang disebutkan dalam urutan kronologis.
1940 - Metode bernama 'Monte Carlo' dikembangkan oleh para peneliti (John von Neumann, Stanislaw Ulan, Edward Teller, Herman Kahn) dan fisikawan yang mengerjakan proyek Manhattan untuk mempelajari hamburan neutron.
1960 - Bahasa simulasi tujuan khusus pertama dikembangkan, seperti SIMSCRIPT oleh Harry Markowitz di RAND Corporation.
1970 - Selama periode ini, penelitian dimulai pada dasar matematika simulasi.
1980 - Selama periode ini, perangkat lunak simulasi berbasis PC, antarmuka pengguna grafis dan pemrograman berorientasi objek dikembangkan.
1990 - Selama periode ini, simulasi berbasis web, grafik animasi mewah, optimasi berbasis simulasi, metode Markov-chain Monte Carlo dikembangkan.
Mengembangkan Model Simulasi
Model simulasi terdiri dari komponen berikut: entitas sistem, variabel input, ukuran kinerja, dan hubungan fungsional. Berikut langkah-langkah untuk mengembangkan model simulasi.
Step 1 - Identifikasi masalah dengan sistem yang ada atau tetapkan persyaratan sistem yang diusulkan.
Step 2 - Rancang masalah sambil memperhatikan faktor dan batasan sistem yang ada.
Step 3 - Kumpulkan dan mulai pemrosesan data sistem, amati kinerja dan hasilnya.
Step 4 - Mengembangkan model menggunakan diagram jaringan dan memverifikasinya dengan berbagai teknik verifikasi.
Step 5 - Validasi model dengan membandingkan kinerjanya dalam berbagai kondisi dengan sistem sebenarnya.
Step 6 - Membuat dokumen model untuk digunakan di masa mendatang, yang mencakup tujuan, asumsi, variabel input, dan kinerja secara rinci.
Step 7 - Pilih desain eksperimental yang sesuai sesuai kebutuhan.
Step 8 - Induksi kondisi eksperimental pada model dan amati hasilnya.
Melakukan Analisis Simulasi
Berikut langkah-langkah untuk melakukan analisis simulasi.
Step 1 - Siapkan pernyataan masalah.
Step 2- Pilih variabel masukan dan buat entitas untuk proses simulasi. Ada dua jenis variabel - variabel keputusan dan variabel yang tidak dapat dikontrol. Variabel keputusan dikendalikan oleh programmer, sedangkan variabel yang tidak dapat dikontrol adalah variabel acak.
Step 3 - Buat batasan pada variabel keputusan dengan menugaskannya ke proses simulasi.
Step 4 - Tentukan variabel keluaran.
Step 5 - Kumpulkan data dari sistem kehidupan nyata untuk dimasukkan ke dalam simulasi.
Step 6 - Kembangkan diagram alur yang menunjukkan kemajuan proses simulasi.
Step 7 - Pilih perangkat lunak simulasi yang sesuai untuk menjalankan model.
Step 8 - Verifikasi model simulasi dengan membandingkan hasilnya dengan sistem real-time.
Step 9 - Lakukan percobaan pada model dengan mengubah nilai variabel untuk menemukan solusi terbaik.
Step 10 - Terakhir, terapkan hasil ini ke dalam sistem waktu nyata.
Pemodelan & Simulasi ─ Keuntungan
Berikut adalah keuntungan menggunakan Pemodelan dan Simulasi -
Easy to understand - Memungkinkan untuk memahami bagaimana sistem benar-benar beroperasi tanpa bekerja pada sistem waktu nyata.
Easy to test - Memungkinkan untuk membuat perubahan pada sistem dan pengaruhnya pada output tanpa bekerja pada sistem waktu nyata.
Easy to upgrade - Memungkinkan untuk menentukan persyaratan sistem dengan menerapkan konfigurasi yang berbeda.
Easy to identifying constraints - Memungkinkan untuk melakukan analisis bottleneck yang menyebabkan keterlambatan dalam proses kerja, informasi, dll.
Easy to diagnose problems- Sistem tertentu begitu kompleks sehingga tidak mudah untuk memahami interaksinya pada satu waktu. Namun, Pemodelan & Simulasi memungkinkan untuk memahami semua interaksi dan menganalisis efeknya. Selain itu, kebijakan, operasi, dan prosedur baru dapat dieksplorasi tanpa mempengaruhi sistem sebenarnya.
Pemodelan & Simulasi ─ Kekurangan
Berikut adalah kerugian menggunakan Pemodelan dan Simulasi -
Merancang model adalah seni yang membutuhkan pengetahuan, pelatihan, dan pengalaman domain.
Operasi dilakukan pada sistem dengan menggunakan bilangan acak, sehingga sulit untuk memprediksi hasilnya.
Simulasi membutuhkan tenaga kerja dan merupakan proses yang memakan waktu.
Hasil simulasi sulit untuk diterjemahkan. Ini membutuhkan ahli untuk memahami.
Proses simulasi itu mahal.
Pemodelan & Simulasi ─ Area Aplikasi
Pemodelan & Simulasi dapat diterapkan pada area berikut - Aplikasi militer, pelatihan & dukungan, perancangan semikonduktor, telekomunikasi, desain & presentasi teknik sipil, dan model E-bisnis.
Selain itu, digunakan untuk mempelajari struktur internal dari sistem yang kompleks seperti sistem biologis. Ini digunakan sambil mengoptimalkan desain sistem seperti algoritme perutean, jalur perakitan, dll. Ini digunakan untuk menguji desain dan kebijakan baru. Ini digunakan untuk memverifikasi solusi analitik.
Pada bab ini, kita akan membahas berbagai konsep dan klasifikasi Pemodelan.
Model & Acara
Berikut adalah konsep dasar Pemodelan & Simulasi.
Object adalah entitas yang ada di dunia nyata untuk mempelajari perilaku model.
Base Model adalah penjelasan hipotetis tentang properti objek dan perilakunya, yang berlaku di seluruh model.
System adalah objek yang diartikulasikan dalam kondisi tertentu, yang ada di dunia nyata.
Experimental Framedigunakan untuk mempelajari sistem di dunia nyata, seperti kondisi eksperimental, aspek, tujuan, dll. Basic Experimental Frame terdiri dari dua set variabel - Variabel Input Frame & Variabel Output Frame, yang cocok dengan terminal sistem atau model. Variabel input Frame bertanggung jawab untuk mencocokkan input yang diterapkan ke sistem atau model. Variabel keluaran Frame bertanggung jawab untuk mencocokkan nilai keluaran ke sistem atau model.
Lumped Model adalah penjelasan yang tepat dari sistem yang mengikuti kondisi yang ditentukan dari Bingkai Eksperimental tertentu.
Verificationadalah proses membandingkan dua item atau lebih untuk memastikan akurasinya. Dalam Pemodelan & Simulasi, verifikasi dapat dilakukan dengan membandingkan konsistensi program simulasi dan model terpusat untuk memastikan performanya. Ada berbagai cara untuk melakukan proses validasi, yang akan kita bahas pada bab tersendiri.
Validationadalah proses membandingkan dua hasil. Pada Pemodelan & Simulasi, validasi dilakukan dengan membandingkan hasil pengukuran eksperimen dengan hasil simulasi dalam konteks Bingkai Eksperimen. Model tidak valid, jika hasilnya tidak sesuai. Ada berbagai cara untuk melakukan proses validasi, yang akan kita bahas di bab terpisah.
Variabel Status Sistem
Variabel status sistem adalah sekumpulan data, yang diperlukan untuk menentukan proses internal dalam sistem pada titik waktu tertentu.
Di sebuah discrete-event model, variabel status sistem tetap konstan selama interval waktu dan nilai berubah pada titik tertentu yang disebut waktu peristiwa.
Di continuous-event model, variabel status sistem ditentukan oleh hasil persamaan diferensial yang nilainya terus berubah dari waktu ke waktu.
Berikut adalah beberapa variabel status sistem -
Entities & Attributes- Entitas merepresentasikan objek yang nilainya bisa statis atau dinamis, bergantung pada proses dengan entitas lain. Atribut adalah nilai lokal yang digunakan oleh entitas.
Resources- Sumber daya adalah entitas yang menyediakan layanan ke satu atau lebih entitas dinamis pada satu waktu. Entitas dinamis dapat meminta satu atau lebih unit sumber daya; jika diterima maka entitas dapat menggunakan sumber daya dan melepaskannya setelah selesai. Jika ditolak, entitas dapat bergabung dengan antrian.
Lists- Daftar digunakan untuk mewakili antrian yang digunakan oleh entitas dan sumber daya. Ada berbagai kemungkinan antrian seperti LIFO, FIFO, dll tergantung pada prosesnya.
Delay - Ini adalah durasi tak terbatas yang disebabkan oleh beberapa kombinasi kondisi sistem.
Klasifikasi Model
Suatu sistem dapat diklasifikasikan ke dalam kategori berikut.
Discrete-Event Simulation Model- Dalam model ini, nilai variabel status hanya berubah pada beberapa titik diskrit dalam waktu terjadinya peristiwa. Peristiwa hanya akan terjadi pada waktu dan penundaan aktivitas yang ditentukan.
Stochastic vs. Deterministic Systems - Sistem stokastik tidak dipengaruhi oleh keacakan dan keluarannya bukan variabel acak, sedangkan sistem deterministik dipengaruhi oleh keacakan dan keluarannya adalah variabel acak.
Static vs. Dynamic Simulation- Simulasi statis mencakup model yang tidak terpengaruh oleh waktu. Contoh: Model Monte Carlo. Simulasi Dinamis mencakup model yang dipengaruhi oleh waktu.
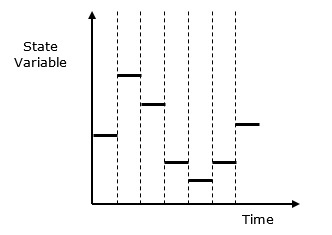
Discrete vs. Continuous Systems- Sistem diskrit dipengaruhi oleh perubahan variabel keadaan pada titik waktu tertentu. Perilakunya digambarkan dalam representasi grafis berikut.
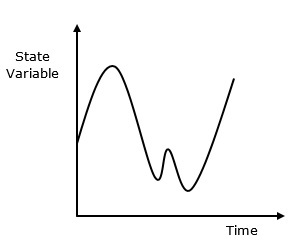
Sistem kontinu dipengaruhi oleh variabel keadaan, yang terus berubah sebagai fungsi seiring waktu. Perilakunya digambarkan dalam representasi grafis berikut.
Proses Pemodelan
Proses pemodelan meliputi langkah-langkah berikut.
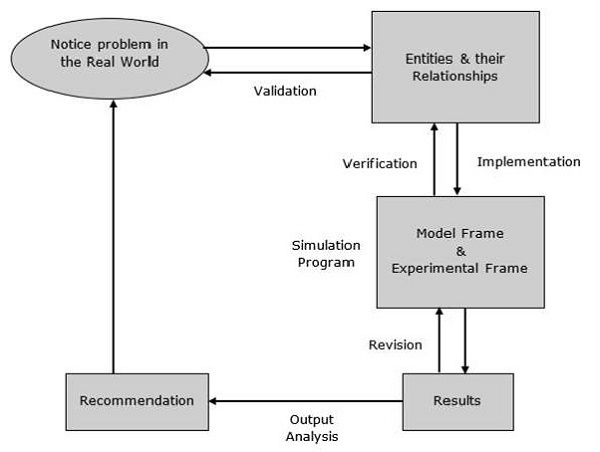
Step 1- Periksa masalahnya. Pada tahap ini kita harus memahami masalah dan memilih klasifikasi yang sesuai, seperti deterministik atau stokastik.
Step 2- Desain model. Pada tahap ini, kita harus melakukan tugas sederhana berikut yang membantu kita mendesain model -
Kumpulkan data sesuai perilaku sistem dan persyaratan di masa mendatang.
Analisis fitur sistem, asumsinya, dan tindakan yang perlu diambil untuk membuat model berhasil.
Tentukan nama variabel, fungsi, unitnya, hubungan, dan aplikasinya yang digunakan dalam model.
Selesaikan model menggunakan teknik yang sesuai dan verifikasi hasilnya menggunakan metode verifikasi. Selanjutnya, validasi hasilnya.
Siapkan laporan yang memuat hasil, interpretasi, kesimpulan, dan saran.
Step 3- Memberikan rekomendasi setelah menyelesaikan seluruh proses yang terkait dengan model. Ini termasuk investasi, sumber daya, algoritma, teknik, dll.
Salah satu masalah nyata yang dihadapi analis simulasi adalah memvalidasi model. Model simulasi hanya valid jika model tersebut merupakan representasi akurat dari sistem aktual, jika tidak model tersebut tidak valid.
Validasi dan verifikasi adalah dua langkah dalam proyek simulasi apa pun untuk memvalidasi model.
Validationadalah proses membandingkan dua hasil. Dalam proses ini, kita perlu membandingkan representasi model konseptual dengan sistem nyata. Jika perbandingannya benar, maka itu valid, jika tidak valid.
Verificationadalah proses membandingkan dua hasil atau lebih untuk memastikan akurasinya. Dalam proses ini, kita harus membandingkan implementasi model dan data yang terkait dengan deskripsi dan spesifikasi konseptual pengembang.

Teknik Verifikasi & Validasi
Ada berbagai teknik yang digunakan untuk melakukan Verifikasi & Validasi Model Simulasi. Berikut adalah beberapa teknik umum -
Teknik Melakukan Verifikasi Model Simulasi
Berikut cara-cara untuk melakukan verifikasi model simulasi -
Dengan menggunakan keterampilan pemrograman untuk menulis dan men-debug program di sub-program.
Dengan menggunakan kebijakan “Penjelajahan Terstruktur” di mana lebih dari satu orang akan membaca program.
Dengan menelusuri hasil antara dan membandingkannya dengan hasil yang diamati.
Dengan memeriksa keluaran model simulasi menggunakan berbagai kombinasi masukan.
Dengan membandingkan hasil simulasi akhir dengan hasil analitik.
Teknik Melakukan Validasi Model Simulasi
Step 1- Desain model dengan validitas tinggi. Ini dapat dicapai dengan menggunakan langkah-langkah berikut -
- Model harus didiskusikan dengan pakar sistem saat mendesain.
- Model harus berinteraksi dengan klien selama proses berlangsung.
- Keluaran harus diawasi oleh ahli sistem.
Step 2- Uji model pada data asumsi. Hal ini dapat dicapai dengan menerapkan data asumsi ke dalam model dan mengujinya secara kuantitatif. Analisis sensitif juga dapat dilakukan untuk mengamati pengaruh perubahan hasil ketika perubahan signifikan dilakukan pada data masukan.
Step 3- Tentukan keluaran perwakilan dari model Simulasi. Ini dapat dicapai dengan menggunakan langkah-langkah berikut -
Tentukan seberapa dekat keluaran simulasi dengan keluaran sistem sebenarnya.
Perbandingan dapat dilakukan dengan menggunakan Uji Turing. Ini menyajikan data dalam format sistem, yang hanya dapat dijelaskan oleh para ahli.
Metode statistik dapat digunakan untuk membandingkan keluaran model dengan keluaran sistem yang sebenarnya.
Perbandingan Data Model dengan Data Nyata
Setelah model dikembangkan, data keluarannya harus dibandingkan dengan data sistem yang sebenarnya. Berikut adalah dua pendekatan untuk melakukan perbandingan ini.
Memvalidasi Sistem yang Ada
Dalam pendekatan ini, kami menggunakan input model dunia nyata untuk membandingkan outputnya dengan input dunia nyata dari sistem nyata. Proses validasi ini sangat mudah, namun mungkin terdapat beberapa kesulitan saat dilakukan, seperti jika output akan dibandingkan dengan rata-rata panjang, waktu tunggu, waktu idle, dll. Dapat dibandingkan menggunakan uji statistik dan pengujian hipotesis. Beberapa uji statistik tersebut adalah uji chi-square, uji Kolmogorov-Smirnov, uji Cramer-von Mises, dan uji Moments.
Memvalidasi Model Pertama Kali
Anggaplah kita harus mendeskripsikan sistem yang diusulkan yang tidak ada saat ini maupun yang telah ada di masa lalu. Oleh karena itu, tidak ada data historis yang tersedia untuk membandingkan kinerjanya. Oleh karena itu, kita harus menggunakan sistem hipotetis berdasarkan asumsi. Mengikuti petunjuk yang berguna akan membantu membuatnya efisien.
Subsystem Validity- Model itu sendiri mungkin tidak memiliki sistem yang ada untuk dibandingkan, tetapi mungkin terdiri dari subsistem yang dikenal. Masing-masing validitas tersebut dapat diuji secara terpisah.
Internal Validity - Model dengan varians internal tingkat tinggi akan ditolak sebagai sistem stokastik dengan varians tinggi karena proses internalnya akan menyembunyikan perubahan output akibat perubahan input.
Sensitivity Analysis - Ini memberikan informasi tentang parameter sensitif dalam sistem yang perlu kita perhatikan lebih tinggi.
Face Validity - Jika model bekerja pada logika yang berlawanan, maka model tersebut harus ditolak meskipun berperilaku seperti sistem sebenarnya.
Dalam sistem diskrit, perubahan status sistem tidak kontinu dan setiap perubahan status sistem disebut event. Model yang digunakan dalam simulasi sistem diskrit memiliki sekumpulan bilangan yang merepresentasikan keadaan sistem, disebut sebagai astate descriptor. Pada bab ini kita juga akan belajar tentang simulasi antrian yang merupakan aspek yang sangat penting dalam simulasi kejadian diskrit bersama dengan simulasi sistem time-sharing.
Berikut adalah representasi grafis dari perilaku simulasi sistem diskrit.
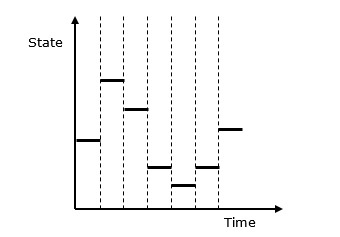
Simulasi Peristiwa Diskrit ─ Fitur Utama
Simulasi kejadian diskrit umumnya dilakukan oleh perangkat lunak yang dirancang dalam bahasa pemrograman tingkat tinggi seperti Pascal, C ++, atau bahasa simulasi khusus lainnya. Berikut adalah lima fitur utama -
Entities - Ini adalah representasi dari elemen nyata seperti bagian-bagian mesin.
Relationships - Itu berarti menghubungkan entitas bersama.
Simulation Executive - Bertanggung jawab untuk mengontrol waktu di muka dan melaksanakan acara diskrit.
Random Number Generator - Ini membantu untuk mensimulasikan data yang berbeda yang masuk ke model simulasi.
Results & Statistics - Ini memvalidasi model dan memberikan ukuran kinerjanya.
Representasi Grafik Waktu
Setiap sistem bergantung pada parameter waktu. Dalam representasi grafis, ini disebut sebagai waktu jam atau penghitung waktu dan awalnya disetel ke nol. Waktu diperbarui berdasarkan dua faktor berikut -
Time Slicing - Ini adalah waktu yang ditentukan oleh model untuk setiap peristiwa hingga tidak adanya peristiwa apa pun.
Next Event- Ini adalah acara yang ditentukan oleh model untuk acara berikutnya yang akan dijalankan, bukan interval waktu. Ini lebih efisien daripada Pengiris Waktu.
Simulasi Sistem Antrian
Antrian adalah kombinasi dari semua entitas dalam sistem yang dilayani dan mereka yang menunggu giliran.
Parameter
Berikut adalah daftar parameter yang digunakan dalam Sistem Antrian.
| Simbol | Deskripsi |
|---|---|
| λ | Menunjukkan tingkat kedatangan yang merupakan jumlah kedatangan per detik |
| Ts | Menunjukkan waktu layanan rata-rata untuk setiap kedatangan tidak termasuk waktu tunggu dalam antrian |
| σTs | Menunjukkan deviasi standar waktu layanan |
| ρ | Menunjukkan pemanfaatan waktu server, baik saat menganggur maupun sibuk |
| u | Menunjukkan intensitas lalu lintas |
| r | Menunjukkan rata-rata item dalam sistem |
| R | Menunjukkan jumlah total item dalam sistem |
| Tr | Menunjukkan waktu rata-rata suatu item dalam sistem |
| TR | Menunjukkan total waktu suatu item dalam sistem |
| σr | Menunjukkan simpangan baku dari r |
| σTr | Menunjukkan deviasi standar dari Tr |
| w | Menunjukkan jumlah rata-rata item yang menunggu dalam antrian |
| σw | Menunjukkan simpangan baku dari w |
| Tw | Menunjukkan waktu tunggu rata-rata untuk semua item |
| Td | Menunjukkan waktu tunggu rata-rata dari item yang menunggu dalam antrian |
| N | Menunjukkan jumlah server dalam suatu sistem |
| mx (y) | Menunjukkan persentil ke y yang berarti nilai y di bawahnya x terjadi y persen dari waktu |
Antrian Server Tunggal
Ini adalah sistem antrian paling sederhana seperti yang ditunjukkan pada gambar berikut. Elemen sentral dari sistem adalah server, yang menyediakan layanan ke perangkat atau item yang terhubung. Item meminta ke sistem untuk dilayani, jika server menganggur. Kemudian, itu disajikan segera, jika tidak bergabung dengan antrian tunggu. Setelah tugas diselesaikan oleh server, item tersebut berangkat.
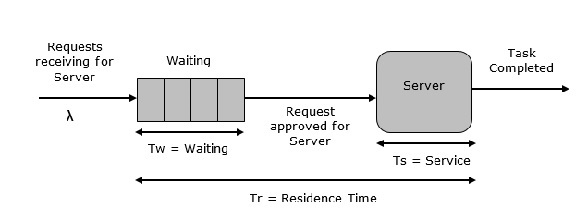
Antrian Multi Server
Seperti namanya, sistem terdiri dari beberapa server dan antrean umum untuk semua item. Ketika ada item yang meminta server, itu dialokasikan jika setidaknya satu server tersedia. Jika tidak, antrian mulai dimulai hingga server bebas. Dalam sistem ini, kami berasumsi bahwa semua server identik, yaitu tidak ada perbedaan server mana yang dipilih untuk item mana.
Ada pengecualian pemanfaatan. MembiarkanN menjadi server yang identik, lalu ρadalah pemanfaatan setiap server. MempertimbangkanNρmenjadi pemanfaatan seluruh sistem; maka pemanfaatannya maksimalN*100%, dan tingkat masukan maksimum adalah -
$ λmax = \ frac {\ teks {N}} {\ teks {T} s} $

Hubungan Antrian
Tabel berikut menunjukkan beberapa hubungan antrian dasar.
| Ketentuan Umum | Server Tunggal | Multi server |
|---|---|---|
| r = λTr Little's formula | ρ = λTs | ρ = λTs / N |
| w = λTw Rumus kecil | r = w + ρ | u = λTs = ρN |
| Tr = Tw + Ts | r = w + Nρ |
Simulasi Sistem Pembagian Waktu
Sistem pembagian waktu dirancang sedemikian rupa sehingga setiap pengguna menggunakan sebagian kecil waktu yang digunakan bersama pada suatu sistem, yang mengakibatkan banyak pengguna berbagi sistem secara bersamaan. Perpindahan setiap pengguna sangat cepat sehingga setiap pengguna merasa seperti menggunakan sistem mereka sendiri. Ini didasarkan pada konsep penjadwalan CPU dan multi-pemrograman di mana banyak sumber daya dapat digunakan secara efektif dengan menjalankan banyak pekerjaan secara bersamaan pada suatu sistem.
Example - Sistem Simulasi SimOS.
Ini dirancang oleh Universitas Stanford untuk mempelajari desain perangkat keras komputer yang kompleks, untuk menganalisis kinerja aplikasi, dan untuk mempelajari sistem operasi. SimOS berisi simulasi perangkat lunak dari semua komponen perangkat keras sistem komputer modern, yaitu prosesor, Memory Management Units (MMU), cache, dll.
Sistem kontinu adalah sistem di mana aktivitas penting dari sistem diselesaikan dengan lancar tanpa penundaan, yaitu tidak ada antrian kejadian, tidak ada penyortiran simulasi waktu, dll. Ketika sistem kontinu dimodelkan secara matematis, variabelnya yang mewakili atribut dikontrol oleh fungsi kontinu .
Apa itu Simulasi Berkelanjutan?
Simulasi kontinu adalah jenis simulasi di mana variabel keadaan berubah terus menerus terhadap waktu. Berikut adalah representasi grafis dari perilakunya.

Mengapa Menggunakan Simulasi Berkelanjutan?
Kami harus menggunakan simulasi kontinu karena bergantung pada persamaan diferensial dari berbagai parameter yang terkait dengan sistem dan hasil perkiraannya yang diketahui oleh kami.
Area Aplikasi
Simulasi berkelanjutan digunakan di sektor-sektor berikut. Di bidang teknik sipil untuk pembangunan tanggul bendungan dan konstruksi terowongan. Dalam aplikasi militer untuk simulasi lintasan rudal, simulasi pelatihan pesawat tempur, dan perancangan & pengujian pengontrol cerdas untuk kendaraan bawah air.
Di bidang logistik untuk perancangan plaza tol, analisis arus penumpang di terminal bandara, dan evaluasi jadwal penerbangan secara proaktif. Dalam pengembangan bisnis untuk perencanaan pengembangan produk, perencanaan manajemen staf, dan analisis studi pasar.
Simulasi Monte Carlo adalah teknik matematika terkomputerisasi untuk menghasilkan data sampel acak berdasarkan beberapa distribusi yang diketahui untuk eksperimen numerik. Metode ini diterapkan pada analisis kuantitatif risiko dan masalah pengambilan keputusan. Metode ini digunakan oleh para profesional dari berbagai profil seperti keuangan, manajemen proyek, energi, manufaktur, teknik, penelitian & pengembangan, asuransi, minyak & gas, transportasi, dll.
Metode ini pertama kali digunakan oleh ilmuwan yang mengerjakan bom atom pada tahun 1940. Metode ini dapat digunakan dalam situasi di mana kita perlu membuat perkiraan dan keputusan yang tidak pasti seperti prediksi ramalan cuaca.
Simulasi Monte Carlo ─ Karakteristik Penting
Berikut adalah tiga karakteristik penting dari metode Monte-Carlo -
- Keluarannya harus menghasilkan sampel acak.
- Distribusi inputnya harus diketahui.
- Hasilnya harus diketahui saat melakukan percobaan.
Simulasi Monte Carlo ─ Keuntungan
- Mudah diimplementasikan.
- Menyediakan sampel statistik untuk eksperimen numerik menggunakan komputer.
- Memberikan solusi perkiraan untuk masalah matematika.
- Dapat digunakan untuk masalah stokastik dan deterministik.
Simulasi Monte Carlo ─ Kekurangan
Memakan waktu karena ada kebutuhan untuk menghasilkan sejumlah besar sampel untuk mendapatkan hasil yang diinginkan.
Hasil dari metode ini hanyalah perkiraan dari nilai sebenarnya, bukan persisnya.
Metode Simulasi Monte Carlo ─ Diagram Alir
Ilustrasi berikut menunjukkan diagram alir umum simulasi Monte Carlo.

Tujuan database dalam Pemodelan & Simulasi adalah untuk menyediakan representasi data dan hubungannya untuk keperluan analisis dan pengujian. Model data pertama diperkenalkan pada tahun 1980 oleh Edgar Codd. Berikut adalah fitur-fitur yang menonjol dari model tersebut.
Database adalah kumpulan objek data berbeda yang mendefinisikan informasi dan hubungannya.
Aturan untuk menentukan batasan pada data di objek.
Operasi dapat diterapkan ke objek untuk mengambil informasi.
Awalnya, Pemodelan Data didasarkan pada konsep entitas & relasi dimana entitas merupakan jenis informasi data, dan relasi merepresentasikan asosiasi antar entitas.
Konsep terbaru untuk pemodelan data adalah desain berorientasi objek di mana entitas direpresentasikan sebagai kelas, yang digunakan sebagai template dalam pemrograman komputer. Kelas yang memiliki nama, atribut, batasan, dan hubungan dengan objek kelas lain.
Representasi dasarnya terlihat seperti -
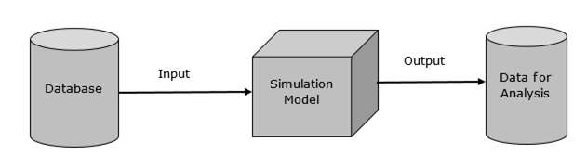
Representasi data
Representasi Data untuk Acara
Peristiwa simulasi memiliki atributnya seperti nama peristiwa dan informasi waktu yang terkait. Ini mewakili pelaksanaan simulasi yang disediakan menggunakan satu set data input yang terkait dengan parameter file input dan memberikan hasilnya sebagai satu set data output, disimpan dalam beberapa file yang terkait dengan file data.
Representasi Data untuk File Input
Setiap proses simulasi memerlukan sekumpulan data masukan yang berbeda dan nilai parameter terkait, yang direpresentasikan dalam file data masukan. File masukan dikaitkan dengan perangkat lunak yang memproses simulasi. Model data mewakili file yang direferensikan oleh asosiasi dengan file data.
Representasi Data untuk File Output
Ketika proses simulasi selesai, ini menghasilkan berbagai file keluaran dan setiap file keluaran direpresentasikan sebagai file data. Setiap file memiliki nama, deskripsi, dan faktor universal. File data diklasifikasikan menjadi dua file. File pertama berisi nilai numerik dan file kedua berisi informasi deskriptif untuk konten file numerik.
Jaringan Neural dalam Pemodelan & Simulasi
Jaringan saraf adalah cabang dari kecerdasan buatan. Jaringan saraf adalah jaringan dari banyak prosesor yang disebut sebagai unit, setiap unit memiliki memori lokalnya yang kecil. Setiap unit dihubungkan oleh saluran komunikasi searah yang disebut sebagai koneksi, yang membawa data numerik. Setiap unit hanya bekerja pada data lokalnya dan pada input yang mereka terima dari koneksi.
Sejarah
Perspektif sejarah simulasi seperti yang disebutkan dalam urutan kronologis.
Model saraf pertama dikembangkan di 1940 oleh McCulloch & Pitts.
Di 1949, Donald Hebb menulis sebuah buku “The Organization of Behavior”, yang menunjuk pada konsep neuron.
Di 1950, dengan komputer yang maju, menjadi mungkin untuk membuat model pada teori-teori ini. Itu dilakukan oleh laboratorium penelitian IBM. Namun, usahanya gagal dan upaya selanjutnya berhasil.
Di 1959, Bernard Widrow dan Marcian Hoff, mengembangkan model yang disebut ADALINE dan MADALINE. Model ini memiliki Beberapa ADAptive LINear Elements. MADALINE adalah jaringan saraf pertama yang diterapkan pada masalah dunia nyata.
Di 1962, model perceptron yang dikembangkan oleh Rosenblatt memiliki kemampuan untuk memecahkan masalah klasifikasi pola sederhana.
Di 1969, Minsky & Papert memberikan bukti matematis tentang keterbatasan model perceptron dalam komputasi. Dikatakan bahwa model perceptron tidak dapat menyelesaikan masalah X-OR. Kelemahan tersebut menyebabkan penurunan sementara jaringan saraf.
Di 1982, John Hopfield dari Caltech mempresentasikan idenya di atas kertas kepada National Academy of Sciences untuk membuat mesin menggunakan garis dua arah. Sebelumnya, garis searah digunakan.
Ketika teknik kecerdasan buatan tradisional yang melibatkan metode simbolik gagal, maka muncul kebutuhan untuk menggunakan jaringan saraf. Jaringan saraf memiliki teknik paralelisme masif, yang menyediakan daya komputasi yang diperlukan untuk memecahkan masalah semacam itu.
Area Aplikasi
Jaringan saraf dapat digunakan dalam mesin sintesis ucapan, untuk pengenalan pola, untuk mendeteksi masalah diagnostik, di papan kontrol robotik dan peralatan medis.
Fuzzy Set dalam Pemodelan & Simulasi
Seperti dibahas sebelumnya, setiap proses simulasi kontinu bergantung pada persamaan diferensial dan parameternya seperti a, b, c, d> 0. Umumnya, perkiraan titik dihitung dan digunakan dalam model. Namun, terkadang estimasi ini tidak pasti sehingga kami membutuhkan bilangan fuzzy dalam persamaan diferensial, yang memberikan estimasi dari parameter yang tidak diketahui.
Apa itu Fuzzy Set?
Dalam himpunan klasik, sebuah elemen bisa menjadi anggota himpunan atau bukan. Himpunan fuzzy didefinisikan dalam himpunan klasikX sebagai -
A = {(x, μA (x)) | x ∈ X}
Case 1 - Fungsinya μA(x) memiliki properti berikut -
∀x ∈ X μA (x) ≥ 0
sup x ∈ X {μA (x)} = 1
Case 2 - Biarkan kabur B didefinisikan sebagai A = {(3, 0.3), (4, 0.7), (5, 1), (6, 0.4)}, maka notasi fuzzy standarnya ditulis sebagai A = {0.3/3, 0.7/4, 1/5, 0.4/6}
Nilai apa pun dengan nilai keanggotaan nol tidak muncul dalam ekspresi himpunan.
Case 3 - Hubungan antara himpunan fuzzy dan himpunan renyah klasik.
Gambar berikut menggambarkan hubungan antara himpunan fuzzy dan himpunan renyah klasik.