Sistem Radar - Pembatalan Saluran Tunda
Dalam bab ini, kita akan mempelajari tentang Pembatalan Garis Tunda dalam Sistem Radar. Seperti namanya, garis tunda memperkenalkan sejumlah penundaan. Jadi, garis penundaan ini terutama digunakan di pembatalan garis penundaan untuk memperkenalkan adelay waktu pengulangan pulsa.
Delay line cancelleradalah filter, yang menghilangkan komponen DC dari sinyal gema yang diterima dari target stasioner. Artinya, komponen AC memungkinkan sinyal gema diterima dari target non-stasioner, yaitu target bergerak.
Jenis Delay Line Cancellers
Pembatalan garis penundaan dapat diklasifikasikan sebagai berikut two types berdasarkan jumlah garis penundaan yang ada di dalamnya.
- Pembatalan Saluran Tunda Tunggal
- Pembatalan Saluran Tunda Ganda
Di bagian selanjutnya, kami akan membahas lebih lanjut tentang dua pembatalan baris Penundaan ini.
Pembatalan Saluran Tunda Tunggal
Kombinasi garis penundaan dan pengurang dikenal sebagai pembatalan garis penundaan. Ini juga disebut pembatal baris Delay tunggal. Itublock diagram Penerima MTI dengan pembatalan baris Delay tunggal ditunjukkan pada gambar di bawah ini.
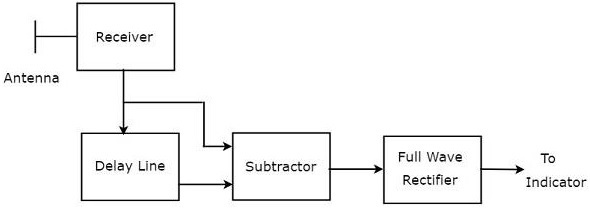
Kita bisa menulis mathematical equation dari sinyal gema yang diterima setelah efek Doppler sebagai -
$$ V_1 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] \: \: \: \: \: Persamaan \: 1 $$
Dimana,
A adalah amplitudo sinyal video
$ f_d $ adalah frekuensi Doppler
$ \ phi_o $ adalah pergeseran fasa dan itu sama dengan $ 4 \ pi f_tR_o / C $
Kami akan mendapatkan output of Delay line canceller, dengan mengganti $ t $ dengan $ t-T_P $ pada Persamaan 1.
$$ V_2 = A \ sin \ kiri [2 \ pi f_d \ kiri (t-T_P \ kanan) - \ phi_0 \ kanan] \: \: \: \: \: Persamaan \: 2 $$
Dimana,
$ T_P $ adalah waktu pengulangan pulsa
Kami akan mendapatkan subtractor output dengan mengurangi Persamaan 2 dari Persamaan 1.
$$ V_1-V_2 = A \ sin \ kiri [2 \ pi f_dt- \ phi_0 \ kanan] -A \ sin \ kiri [2 \ pi f_d \ kiri (t-T_P \ kanan) - \ phi_0 \ kanan] $$
$$ \ Rightarrow V_1-V_2 = 2A \ sin \ kiri [\ frac {2 \ pi f_dt- \ phi_0- \ kiri [2 \ pi f_d \ kiri (t-T_P \ kanan) - \ phi_0 \ kanan]} {2 } \ kanan] \ cos \ kiri [\ frac {2 \ pi f_dt- \ phi_o + 2 \ pi f_d \ kiri (t-T_P \ kanan) - \ phi_0} {2} \ kanan] $$
$$ V_1-V_2 = 2A \ sin \ kiri [\ frac {2 \ pi f_dT_P} {2} \ kanan] \ cos \ kiri [\ frac {2 \ pi f_d \ kiri (2t-T_P \ kanan) -2 \ phi_0} {2} \ kanan] $$
$$ \ Rightarrow V_1-V_2 = 2A \ sin \ kiri [\ pi f_dT_p \ kanan] \ cos \ kiri [2 \ pi f_d \ kiri (t- \ frac {T_P} {2} \ kanan) - \ phi_0 \ kanan ] \: \: \: \: \: Persamaan \: 3 $$
Keluaran pengurang diterapkan sebagai masukan ke Penyearah Gelombang Penuh. Oleh karena itu, keluaran dari Penyearah Gelombang Penuh terlihat seperti yang ditunjukkan pada gambar berikut. Ini tidak lain adalahfrequency response pembatalan baris penundaan tunggal.

Dari persamaan 3 kita dapat mengamati bahwa respon frekuensi dari pembatal baris tunda tunggal menjadi nol, bila $ \ pi f_dT_P $ sama dengan integer multiples of $ \ pi $ Artinya, $ \ pi f_dT_P $ sama dengan $ n \ pi $ Secara matematis, dapat ditulis sebagai
$$ \ pi f_dT_P = n \ pi $$
$$ \ Rightarrow f_dT_P = n $$
$$ \ Rightarrow f_d = \ frac {n} {T_P} \: \: \: \: \: Persamaan \: 4 $$
Dari persamaan 4 dapat disimpulkan bahwa respon frekuensi dari pembatal delay line menjadi nol, ketika frekuensi Doppler $ f_d $ sama dengan kelipatan integer kebalikan dari waktu pengulangan pulsa $ T_P $.
Kita mengetahui hubungan berikut antara waktu pengulangan denyut dan frekuensi pengulangan denyut.
$$ f_d = \ frac {1} {T_P} $$
$$ \ Rightarrow \ frac {1} {T_P} = f_P \: \: \: \: \: Persamaan \: 5 $$
Kita akan mendapatkan persamaan berikut, dengan mengganti Persamaan 5 pada Persamaan 4.
$$ \ Rightarrow f_d = nf_P \: \: \: \: \: Persamaan \: 6 $$
Dari persamaan 6 dapat disimpulkan bahwa respon frekuensi dari pembatal delay line menjadi nol, bila frekuensi Doppler $ f_d $ sama dengan kelipatan integer frekuensi pengulangan pulsa $ f_P $.
Kecepatan Buta
Dari apa yang kita pelajari sejauh ini, pembatal baris Delay tunggal menghilangkan komponen DC dari sinyal gema yang diterima dari target stasioner, ketika $ n $ sama dengan nol. Selain itu, juga menghilangkan komponen AC dari sinyal echo yang diterima dari target non-stasioner, ketika frekuensi Doppler $ f_d $ sama dengan integer(other than zero) kelipatan frekuensi pengulangan pulsa $ f_P $.
Jadi, kecepatan relatif dimana respon frekuensi dari pembatal garis penundaan tunggal menjadi nol disebut blind speeds. Secara matematis, kita dapat menulis ekspresi untuk kecepatan buta $ v_n $ sebagai -
$$ v_n = \ frac {n \ lambda} {2T_P} \: \: \: \: \: Persamaan \: 7 $$
$$ \ Rightarrow v_n = \ frac {n \ lambda f_P} {2} \: \: \: \: \: Persamaan \: 8 $$
Dimana,
$ n $ adalah bilangan bulat dan sama dengan 1, 2, 3, dan seterusnya
$ \ lambda $ adalah panjang gelombang operasi
Contoh Soal
Radar MTI beroperasi pada frekuensi $ 6GHZ $ dengan frekuensi pengulangan pulsa $ 1KHZ $. Temukan yang pertama, kedua dan ketigablind speeds dari Radar ini.
Larutan
Diberikan,
Frekuensi operasi MTI Radar, $ f = 6GHZ $
Frekuensi pengulangan pulsa, $ f_P = 1KHZ $.
Berikut rumusnya operating wavelength $ \ lambda $ dalam hal frekuensi operasi, f.
$$ \ lambda = \ frac {C} {f} $$
Gantikan, $ C = 3 \ times10 ^ 8m / sec $ dan $ f = 6GHZ $ dalam persamaan di atas.
$$ \ lambda = \ frac {3 \ times10 ^ 8} {6 \ times10 ^ 9} $$
$$ \ Rightarrow \ lambda = 0.05m $$
Sehingga operating wavelength $ \ lambda $ sama dengan $ 0,05 juta $, jika frekuensi operasi f adalah $ 6GHZ $.
Kami tahu yang berikut ini formula for blind speed.
$$ v_n = \ frac {n \ lambda f_p} {2} $$
Dengan mengganti, $ n $ = 1,2 & 3 pada persamaan di atas, kita akan mendapatkan persamaan berikut untuk kecepatan buta pertama, kedua & ketiga.
$$ v_1 = \ frac {1 \ times \ lambda f_p} {2} = \ frac {\ lambda f_p} {2} $$
$$ v_2 = \ frac {2 \ times \ lambda f_p} {2} = 2 \ kiri (\ frac {\ lambda f_p} {2} \ kanan) = 2v_1 $$
$$ v_3 = \ frac {3 \ times \ lambda f_p} {2} = 3 \ kiri (\ frac {\ lambda f_p} {2} \ kanan) = 3v_1 $$
Substitute nilai $ \ lambda $ dan $ f_P $ dalam persamaan kecepatan buta pertama.
$$ v_1 = \ frac {0,05 \ kali 10 ^ 3} {2} $$
$$ \ Rightarrow v_1 = 25m / dtk $$
Oleh karena itu, first blind speed $ v_1 $ sama dengan $ 25m / detik $ untuk spesifikasi yang diberikan.
Kami akan mendapatkan nilai second & third blind speeds sebagai $ 50 juta / detik $ & $ 75 juta / detik $ masing-masing dengan mengganti nilai 1 dalam persamaan kecepatan buta kedua & ketiga.
Pembatalan Saluran Tunda Ganda
Kita tahu bahwa pembatal garis penundaan tunggal terdiri dari garis penundaan dan pengurang. Jika dua pembatalan garis penundaan tersebut di-cascade bersama-sama, maka kombinasi tersebut disebut pembatalan garis penundaan ganda. Itublock diagram Pembatalan garis penundaan ganda ditunjukkan pada gambar berikut.

Misalkan $ p \ left (t \ right) $ dan $ q \ left (t \ right) $ menjadi masukan dan keluaran dari pembatalan baris tunda pertama. Kita akan mendapatkan relasi matematis berikut darifirst delay line canceller.
$$ q \ kiri (t \ kanan) = p \ kiri (t \ kanan) -p \ kiri (t-T_P \ kanan) \: \: \: \: \: Persamaan \: 9 $$
Keluaran pembatal saluran tunda pertama diterapkan sebagai masukan untuk pembatal saluran tunda kedua. Karenanya, $ q \ left (t \ right) $ akan menjadi input pembatalan baris penundaan kedua. Misalkan $ r \ left (t \ right) $ menjadi output dari pembatal baris penundaan kedua. Kita akan mendapatkan relasi matematis berikut darisecond delay line canceller.
$$ r \ left (t \ right) = q \ left (t \ right) -q \ left (t-T_P \ right) \: \: \: \: \: Persamaan \: 10 $$
Gantikan $ t $ dengan $ t-T_P $ pada Persamaan 9.
$$ q \ kiri (t-T_P \ kanan) = p \ kiri (t-T_P \ kanan) -p \ kiri (t-T_P-T_P \ kanan) $$
$$ q \ kiri (t-T_P \ kanan) = p \ kiri (t-T_P \ kanan) -p \ kiri (t-2T_P \ kanan) \: \: \: \: \: Persamaan \: 11 $$
Substitute, Persamaan 9 dan Persamaan 11 pada Persamaan 10.
$$ r \ kiri (t \ kanan) = p \ kiri (t \ kanan) -p \ kiri (t-T_P \ kanan) - \ kiri [p \ kiri (t-T_P \ kanan) -p \ kiri (t -2T_P \ kanan) \ kanan] $$
$$ \ Rightarrow r \ left (t \ right) = p \ kiri (t \ kanan) -2p \ kiri (t-T_P \ kanan) + p \ kiri (t-2T_P \ kanan) \: \: \: \ : \: Persamaan \: 12 $$
Itu advantagedari pembatalan garis penundaan ganda adalah menolak kekacauan secara luas. Output dari dua pembatal delay line, yang di-cascade, akan sama dengan kuadrat dari output pembatal delay line.
Jadi, besarnya output pembatal delay line ganda yang ada pada MTI Radar receiver akan sama dengan $ 4A ^ 2 \ left (\ sin \ left [\ pi f_dT_P \ right] \ right) ^ 2 $.

Karakteristik respons frekuensi dari pembatal saluran penundaan ganda dan kombinasi bertingkat dari dua pembatal saluran penundaan adalah sama. Ituadvantage pembatalan garis penundaan domain waktu adalah bahwa itu dapat dioperasikan untuk semua rentang frekuensi.