Menganalisis Data Pengukuran Perangkat Lunak
Setelah mengumpulkan data yang relevan, kami harus menganalisisnya dengan cara yang tepat. Ada tiga item utama yang perlu dipertimbangkan untuk memilih teknik analisis.
- Sifat data
- Tujuan percobaan
- Pertimbangan desain
Sifat Data
Untuk menganalisis data, kita juga harus melihat populasi yang lebih besar yang direpresentasikan oleh data serta sebaran datanya.
Pengambilan sampel, populasi, dan distribusi data
Sampling adalah proses memilih sekumpulan data dari populasi yang besar. Statistik sampel mendeskripsikan dan meringkas ukuran yang diperoleh dari sekelompok subjek eksperimen.
Parameter populasi mewakili nilai-nilai yang akan diperoleh jika semua kemungkinan subjek diukur.
Populasi atau sampel dapat dijelaskan dengan ukuran tendensi sentral seperti mean, median, dan mode dan ukuran dispersi seperti varians dan deviasi standar. Banyak kumpulan data yang didistribusikan secara normal seperti yang ditunjukkan pada grafik berikut.
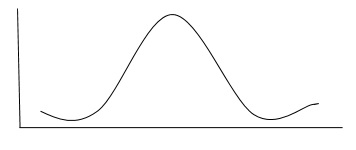
Seperti yang ditunjukkan di atas, data tentang mean akan didistribusikan secara merata. yang merupakan karakteristik signifikan dari distribusi normal.
Distribusi lain juga ada di mana datanya miring sehingga ada lebih banyak titik data di satu sisi mean daripada yang lain. Sebagai contoh: Jika sebagian besar data ada di sisi kiri mean, maka kita dapat mengatakan bahwa distribusinya miring ke kiri.
Tujuan Eksperimen
Biasanya, eksperimen dilakukan -
- Untuk mengkonfirmasi teori
- Untuk mengeksplorasi suatu hubungan
Untuk mencapai masing-masing, tujuan harus dinyatakan secara formal dalam bentuk hipotesis, dan analisis harus membahas hipotesis secara langsung.
Untuk mengkonfirmasi teori
Investigasi harus dirancang untuk mengeksplorasi kebenaran sebuah teori. Teori biasanya menyatakan bahwa penggunaan metode, alat, atau teknik tertentu memiliki efek tertentu pada subjek, membuatnya lebih baik dalam beberapa hal daripada yang lain.
Ada dua kasus data yang harus dipertimbangkan: normal data dan non-normal data.
Jika data berdistribusi normal dan terdapat dua kelompok yang dibandingkan maka uji t siswa dapat digunakan untuk analisis. Jika ada lebih dari dua kelompok untuk dibandingkan, analisis umum dari uji varians yang disebut F-statistik dapat digunakan.
Jika datanya tidak normal, maka data tersebut dapat dianalisis menggunakan uji Kruskal-Wallis dengan cara memeringkatnya.
Untuk mengeksplorasi suatu hubungan
Investigasi dirancang untuk menentukan hubungan antara titik data yang menggambarkan satu variabel atau beberapa variabel.
Ada tiga teknik untuk menjawab pertanyaan tentang suatu hubungan: plot kotak, plot sebar, dan analisis korelasi.
SEBUAH box plot dapat mewakili ringkasan rentang sekumpulan data.
SEBUAH scatter plot mewakili hubungan antara dua variabel.
Correlation analysis menggunakan metode statistik untuk memastikan apakah ada hubungan yang benar antara dua atribut.
Untuk nilai terdistribusi normal, gunakan Pearson Correlation Coefficient untuk memeriksa apakah kedua variabel berkorelasi tinggi atau tidak.
Untuk data non-normal, rangking data dan gunakan Spearman Rank Correlation Coefficientsebagai ukuran asosiasi. Ukuran lain untuk data non-normal adalahKendall robust correlation coefficient, yang menyelidiki hubungan antara pasangan titik data dan dapat mengidentifikasi korelasi parsial.
Jika peringkat berisi sejumlah besar nilai terikat, a chi-squared testpada tabel kontingensi dapat digunakan untuk menguji hubungan antar variabel. Demikian pula,linear regression dapat digunakan untuk menghasilkan persamaan untuk menggambarkan hubungan antar variabel.
Untuk lebih dari dua variabel, multivariate regression dapat digunakan.
Pertimbangan Desain
Desain investigasi harus dipertimbangkan saat memilih teknik analisis. Pada saat yang sama, kompleksitas analisis dapat mempengaruhi desain yang dipilih. Beberapa kelompok menggunakan F-statistik daripada uji-T Student dengan dua kelompok.
Untuk desain faktorial yang kompleks dengan lebih dari dua faktor, diperlukan uji asosiasi dan signifikansi yang lebih canggih.
Teknik statistik dapat digunakan untuk menjelaskan pengaruh satu set variabel pada yang lain, atau untuk mengkompensasi waktu atau efek pembelajaran.