Ottimizzazione utilizzando la rete Hopfield
L'ottimizzazione è un'azione per rendere qualcosa come il design, la situazione, la risorsa e il sistema il più efficace possibile. Utilizzando una somiglianza tra la funzione di costo e la funzione di energia, possiamo usare neuroni altamente interconnessi per risolvere problemi di ottimizzazione. Un tale tipo di rete neurale è la rete di Hopfield, che consiste in un singolo strato contenente uno o più neuroni ricorrenti completamente connessi. Questo può essere utilizzato per l'ottimizzazione.
Punti da ricordare durante l'utilizzo della rete Hopfield per l'ottimizzazione -
La funzione energetica deve essere minima della rete.
Troverà una soluzione soddisfacente piuttosto che selezionarne uno tra i modelli memorizzati.
La qualità della soluzione trovata dalla rete Hopfield dipende in modo significativo dallo stato iniziale della rete.
Problema del commesso viaggiatore
Trovare il percorso più breve percorso dal venditore è uno dei problemi di calcolo, che può essere ottimizzato utilizzando la rete neurale di Hopfield.
Concetto di base di TSP
Il problema del venditore ambulante (TSP) è un classico problema di ottimizzazione in cui un venditore deve viaggiare ncittà, che sono collegate tra loro, mantenendo al minimo il costo e la distanza percorsa. Ad esempio, il venditore deve viaggiare per un set di 4 città A, B, C, D e l'obiettivo è trovare il tour circolare più breve, ABC – D, in modo da ridurre al minimo il costo, che include anche il costo del viaggio da l'ultima città D alla prima città A.
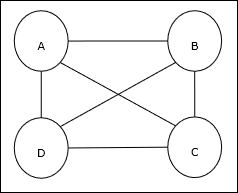
Rappresentazione a matrice
In realtà ogni tour di n-città TSP può essere espresso come n × n matrice cui ith riga descrive il ithposizione della città. Questa matrice,M, per 4 città A, B, C, D può essere espresso come segue:
$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$
Soluzione di Hopfield Network
Pur considerando la soluzione di questo TSP dalla rete Hopfield, ogni nodo della rete corrisponde a un elemento nella matrice.
Calcolo della funzione energetica
Per essere la soluzione ottimizzata, la funzione energetica deve essere minima. Sulla base dei seguenti vincoli, possiamo calcolare la funzione energetica come segue:
Vincolo-I
Il primo vincolo, sulla base del quale calcoleremo la funzione energetica, è che un elemento deve essere uguale a 1 in ogni riga della matrice M e gli altri elementi in ogni riga devono essere uguali a 0perché ogni città può essere presente in una sola posizione nel tour TSP. Questo vincolo può essere matematicamente scritto come segue:
$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: for \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Ora la funzione energetica da minimizzare, in base al vincolo di cui sopra, conterrà un termine proporzionale a -
$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
Vincolo-II
Come sappiamo, in TSP una città può trovarsi in qualsiasi posizione del tour, quindi in ogni colonna della matrice M, un elemento deve essere uguale a 1 e gli altri elementi devono essere uguali a 0. Questo vincolo può essere matematicamente scritto come segue:
$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: for \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Ora la funzione energetica da minimizzare, in base al vincolo di cui sopra, conterrà un termine proporzionale a -
$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
Calcolo della funzione di costo
Supponiamo che una matrice quadrata di (n × n) denotato da C denota la matrice dei costi di TSP per n città dove n > 0. Di seguito sono riportati alcuni parametri durante il calcolo della funzione di costo:
Cx, y - L'elemento della matrice dei costi indica il costo del viaggio dalla città x per y.
L'adiacenza degli elementi di A e B può essere mostrata dalla seguente relazione:
$$ M_ {x, i} \: = \: 1 \: \: e \: \: M_ {y, i \ pm 1} \: = \: 1 $$
Come sappiamo, in Matrix il valore di output di ogni nodo può essere 0 o 1, quindi per ogni coppia di città A, B possiamo aggiungere i seguenti termini alla funzione energia -
$$ \ displaystyle \ sum \ limits_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$
Sulla base della funzione di costo e del valore di vincolo di cui sopra, la funzione energetica finale E può essere dato come segue:
$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {x} \ displaystyle \ sum \ limits_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$
$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limits_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limits_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ limits_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$
Qui, γ1 e γ2 sono due costanti di pesatura.