Progettazione del compilatore - Analisi della sintassi

L'analisi della sintassi o l'analisi è la seconda fase di un compilatore. In questo capitolo apprenderemo i concetti di base usati nella costruzione di un parser.

Abbiamo visto che un analizzatore lessicale può identificare i token con l'aiuto di espressioni regolari e regole di pattern. Ma un analizzatore lessicale non può controllare la sintassi di una data frase a causa dei limiti delle espressioni regolari. Le espressioni regolari non possono controllare i token di bilanciamento, come le parentesi. Pertanto, questa fase utilizza la grammatica senza contesto (CFG), riconosciuta dagli automi push-down.

CFG, d'altra parte, è un superset di Regular Grammar, come illustrato di seguito:

Ciò implica che ogni grammatica regolare è anche priva di contesto, ma esistono alcuni problemi che esulano dallo scopo della grammatica regolare. CFG è uno strumento utile per descrivere la sintassi dei linguaggi di programmazione.

Grammatica senza contesto

In questa sezione, vedremo prima la definizione di grammatica libera dal contesto e introdurremo le terminologie utilizzate nella tecnologia di analisi.

Una grammatica senza contesto ha quattro componenti:

Un insieme di non-terminals(V). I non terminali sono variabili sintattiche che denotano insiemi di stringhe. I non terminali definiscono insiemi di stringhe che aiutano a definire il linguaggio generato dalla grammatica.
Un set di gettoni, noto come terminal symbols(Σ). I terminali sono i simboli di base da cui sono formate le stringhe.
Un insieme di productions(P). Le produzioni di una grammatica specificano il modo in cui i terminali e i non terminali possono essere combinati per formare stringhe. Ogni produzione è composta da un filenon-terminal chiamato il lato sinistro della produzione, una freccia e una sequenza di gettoni e / o on- terminals, chiamato il lato destro della produzione.
Uno dei non terminali è designato come il simbolo di inizio (S); da dove inizia la produzione.

Le stringhe sono derivate dal simbolo di inizio sostituendo ripetutamente un non terminale (inizialmente il simbolo di inizio) dal lato destro di una produzione, per quel non terminale.

Esempio

Prendiamo il problema del linguaggio palindromo, che non può essere descritto mediante l'espressione regolare. Cioè, L = {w | w = w ^R } non è una lingua normale. Ma può essere descritto mediante CFG, come illustrato di seguito:

G = ( V, Σ, P, S )

Dove:

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

Questa grammatica descrive il linguaggio palindromo, come ad esempio: 1001, 11100111, 00100, 1010101, 11111, ecc.

Analizzatori di sintassi

Un analizzatore di sintassi o parser prende l'input da un analizzatore lessicale sotto forma di flussi di token. Il parser analizza il codice sorgente (flusso di token) rispetto alle regole di produzione per rilevare eventuali errori nel codice. L'output di questa fase è un fileparse tree.

In questo modo, il parser esegue due attività, ovvero analizzare il codice, cercare errori e generare un albero di analisi come output della fase.

Ci si aspetta che i parser analizzino l'intero codice anche se nel programma sono presenti alcuni errori. I parser utilizzano strategie di ripristino degli errori, che impareremo più avanti in questo capitolo.

Derivazione

Una derivazione è fondamentalmente una sequenza di regole di produzione, al fine di ottenere la stringa di input. Durante l'analisi, prendiamo due decisioni per una forma di input sentenziale:

Decidere il non terminale che deve essere sostituito.
Decidere la regola di produzione, con la quale verrà sostituito il non terminale.

Per decidere quale non terminale sostituire con la regola di produzione, possiamo avere due opzioni.

Derivazione più a sinistra

Se la forma sentenziale di un input viene scansionata e sostituita da sinistra a destra, viene chiamata derivazione più a sinistra. La forma sentenziale derivata dalla derivazione più a sinistra è chiamata la forma sentenziale a sinistra.

Derivazione più a destra

Se scansioniamo e sostituiamo l'input con regole di produzione, da destra a sinistra, è noto come derivazione più a destra. La forma sentenziale derivata dalla derivazione più a destra è chiamata la forma sentenziale a destra.

Example

Regole di produzione:

E → E + E
E → E * E
E → id

Stringa di input: id + id * id

La derivazione più a sinistra è:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

Si noti che il non terminale più a sinistra viene sempre elaborato per primo.

La derivazione più a destra è:

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

Parse Tree

Un albero di analisi è una rappresentazione grafica di una derivazione. È conveniente vedere come le stringhe vengono derivate dal simbolo di inizio. Il simbolo di inizio della derivazione diventa la radice dell'albero di analisi. Vediamolo con un esempio tratto dall'ultimo argomento.

Prendiamo la derivazione più a sinistra di a + b * c

La derivazione più a sinistra è:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

Passo 1:

E → E * E

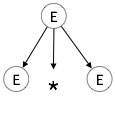
Passo 2:

E → E + E * E

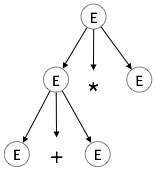
Passaggio 3:

E → id + E * E

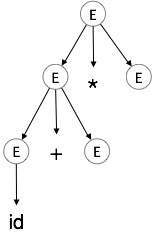
Passaggio 4:

E → id + id * E

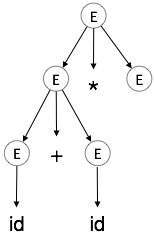
Passaggio 5:

E → id + id * id

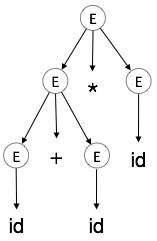
In un albero di analisi:

Tutti i nodi foglia sono terminali.
Tutti i nodi interni non sono terminali.
L'attraversamento in ordine fornisce la stringa di input originale.

Un albero di analisi descrive l'associatività e la precedenza degli operatori. Il sottoalbero più profondo viene attraversato per primo, quindi l'operatore in quel sottoalbero ha la precedenza sull'operatore che si trova nei nodi padre.

Ambiguità

Si dice che una grammatica G sia ambigua se ha più di un albero di analisi (derivazione sinistra o destra) per almeno una stringa.

Example

E → E + E
E → E – E
E → id

Per la stringa id + id - id, la grammatica precedente genera due alberi di analisi:

Si dice che la lingua generata da una grammatica ambigua sia inherently ambiguous. L'ambiguità grammaticale non è buona per la costruzione di un compilatore. Nessun metodo può rilevare e rimuovere automaticamente l'ambiguità, ma può essere rimossa riscrivendo l'intera grammatica senza ambiguità o impostando e rispettando i vincoli di associatività e di precedenza.

Associatività

Se un operando ha operatori su entrambi i lati, il lato da cui l'operatore prende questo operando è deciso dall'associatività di quegli operatori. Se l'operazione è associativa a sinistra, l'operando verrà preso dall'operatore di sinistra o se l'operazione è associativa a destra, l'operatore di destra prenderà l'operando.

Example

Operazioni come addizione, moltiplicazione, sottrazione e divisione sono associative a sinistra. Se l'espressione contiene:

id op id op id

sarà valutato come:

(id op id) op id

Ad esempio, (id + id) + id

Operazioni come l'elevazione a potenza sono associative rette, ovvero l'ordine di valutazione nella stessa espressione sarà:

id op (id op id)

Ad esempio, id ^ (id ^ id)

Precedenza

Se due operatori diversi condividono un operando comune, la precedenza degli operatori decide quale utilizzerà l'operando. Cioè, 2 + 3 * 4 può avere due alberi di analisi diversi, uno corrispondente a (2 + 3) * 4 e un altro corrispondente a 2+ (3 * 4). Impostando la precedenza tra gli operatori, questo problema può essere facilmente rimosso. Come nell'esempio precedente, matematicamente * (moltiplicazione) ha la precedenza su + (addizione), quindi l'espressione 2 + 3 * 4 sarà sempre interpretata come:

2 + (3 * 4)

Questi metodi riducono le possibilità di ambiguità in una lingua o nella sua grammatica.

Ricorsione a sinistra

Una grammatica diventa ricorsiva a sinistra se ha una "A" non terminale la cui derivazione contiene la "A" stessa come simbolo più a sinistra. La grammatica ricorsiva a sinistra è considerata una situazione problematica per i parser top-down. I parser top-down iniziano ad analizzare dal simbolo Start, che di per sé non è terminale. Quindi, quando il parser incontra lo stesso non terminale nella sua derivazione, diventa difficile per lui giudicare quando interrompere l'analisi del non terminale sinistro e entra in un ciclo infinito.

Example:

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1) è un esempio di ricorsione sinistra immediata, dove A è un qualsiasi simbolo non terminale e α rappresenta una stringa di non terminali.

(2) è un esempio di ricorsione indiretta a sinistra.

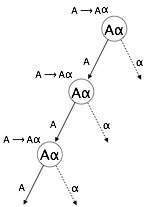
Un parser top-down analizzerà prima il LA, che a sua volta produrrà una stringa composta da A stesso e il parser potrebbe entrare in un ciclo per sempre.

Rimozione della ricorsione a sinistra

Un modo per rimuovere la ricorsione a sinistra consiste nell'usare la seguente tecnica:

La produzione

A => Aα | β

viene convertito nelle seguenti produzioni

A => βA'
A'=> αA' | ε

Ciò non influisce sulle stringhe derivate dalla grammatica, ma rimuove la ricorsione a sinistra immediata.

Il secondo metodo consiste nell'utilizzare il seguente algoritmo, che dovrebbe eliminare tutte le ricorsioni a sinistra dirette e indirette.

START

Arrange non-terminals in some order like A1, A2, A3,…, A_n

   for each i from 1 to n
      {
      for each j from 1 to i-1
         {
         replace each production of form A_i ⟹Aj
         with A_i ⟹ δ1  | δ2 | δ3 |…|  
         where A_j ⟹ δ₁ | δ₂|…| δ_n  are current A_j productions
         }
      }
   eliminate immediate left-recursion
   
END

Example

Il set di produzione

S => Aα | β 
A => Sd

dopo aver applicato l'algoritmo di cui sopra, dovrebbe diventare

S => Aα | β 
A => Aαd | βd

e quindi, rimuovere la ricorsione sinistra immediata utilizzando la prima tecnica.

A  => βdA'
A' => αdA' | ε

Ora nessuna delle produzioni ha una ricorsione a sinistra diretta o indiretta.

Factoring sinistro

Se più di una regola di produzione grammaticale ha una stringa di prefisso comune, il parser top-down non può scegliere quale produzione deve prendere per analizzare la stringa in mano.

Example

Se un parser top-down incontra una produzione come

A ⟹ αβ | α | …

Quindi non può determinare quale produzione seguire per analizzare la stringa poiché entrambe le produzioni iniziano dallo stesso terminale (o non terminale). Per rimuovere questa confusione, utilizziamo una tecnica chiamata factoring a sinistra.

Il factoring a sinistra trasforma la grammatica per renderla utile per i parser top-down. In questa tecnica, facciamo una produzione per ogni prefisso comune e il resto della derivazione viene aggiunto da nuove produzioni.

Example

Le produzioni di cui sopra possono essere scritte come

A => αA'
A'=> β |  | …

Ora il parser ha una sola produzione per prefisso che rende più facile prendere decisioni.

Primo e seguito di serie

Una parte importante della costruzione della tabella parser è creare i primi e i seguenti insiemi. Questi insiemi possono fornire la posizione effettiva di qualsiasi terminale nella derivazione. Questo viene fatto per creare la tabella di analisi in cui la decisione di sostituire T [A, t] = α con qualche regola di produzione.

Primo set

Questo set viene creato per sapere quale simbolo di terminale è derivato nella prima posizione da un non terminale. Per esempio,

α → t β

Cioè α deriva t (terminale) nella primissima posizione. Quindi, t ∈ PRIMO (α).

Algoritmo per il calcolo del primo set

Guarda la definizione di PRIMO (α) insieme:

se α è un terminale, allora PRIMO (α) = {α}.
se α è un non terminale e α → ℇ è una produzione, allora PRIMO (α) = {ℇ}.
se α è un non terminale e α → 1 2 3… ne ogni FIRST () contiene t allora t è in FIRST (α).

Il primo set può essere visto come:

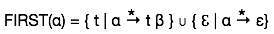
Segui Set

Allo stesso modo, calcoliamo quale simbolo terminale segue immediatamente un α non terminale nelle regole di produzione. Non consideriamo cosa può generare il non terminale ma vediamo invece quale sarebbe il prossimo simbolo di terminale che segue le produzioni di un non terminale.

Algoritmo per il calcolo del set di follow:

se α è un simbolo di inizio, allora FOLLOW () = $
se α è un non terminale e ha una produzione α → AB, allora FIRST (B) è in FOLLOW (A) eccetto ℇ.
se α è un non terminale e ha una produzione α → AB, dove B ℇ, allora FOLLOW (A) è in FOLLOW (α).

Follow set può essere visto come: FOLLOW (α) = {t | S * αt *}

Limitazioni degli analizzatori di sintassi

Gli analizzatori di sintassi ricevono i loro input, sotto forma di token, dagli analizzatori lessicali. Gli analizzatori lessicali sono responsabili della validità di un token fornito dall'analizzatore di sintassi. Gli analizzatori di sintassi presentano i seguenti inconvenienti:

non può determinare se un token è valido,
non può determinare se un token viene dichiarato prima di essere utilizzato,
non può determinare se un token è inizializzato prima di essere utilizzato,
non può determinare se un'operazione eseguita su un tipo di token è valida o meno.

Questi compiti sono svolti dall'analizzatore semantico, che studieremo in Analisi semantica.