Trasformazione 2D

Trasformazione significa cambiare alcuni elementi grafici in qualcos'altro applicando delle regole. Possiamo avere vari tipi di trasformazioni come traslazione, scala in alto o in basso, rotazione, inclinazione, ecc. Quando una trasformazione avviene su un piano 2D, si chiama trasformazione 2D.

Le trasformazioni giocano un ruolo importante nella computer grafica per riposizionare la grafica sullo schermo e cambiarne le dimensioni o l'orientamento.

Coordinate omogenee

Per eseguire una sequenza di trasformazione come la traslazione seguita da rotazione e ridimensionamento, dobbiamo seguire un processo sequenziale:

Traduci le coordinate,
Ruota le coordinate tradotte e poi
Scala le coordinate ruotate per completare la trasformazione composita.

Per abbreviare questo processo, dobbiamo usare la matrice di trasformazione 3 × 3 invece della matrice di trasformazione 2 × 2. Per convertire una matrice 2 × 2 in una matrice 3 × 3, dobbiamo aggiungere una coordinata fittizia extra W.

In questo modo, possiamo rappresentare il punto con 3 numeri invece di 2 numeri, che viene chiamato Homogenous Coordinatesistema. In questo sistema, possiamo rappresentare tutte le equazioni di trasformazione nella moltiplicazione di matrici. Qualsiasi punto cartesiano P (X, Y) può essere convertito in coordinate omogenee da P '(X _h , Y _h , h).

Traduzione

Una traduzione sposta un oggetto in una posizione diversa sullo schermo. È possibile tradurre un punto in 2D aggiungendo le coordinate di traslazione (t _x , t _y ) alla coordinata originale (X, Y) per ottenere la nuova coordinata (X ', Y').

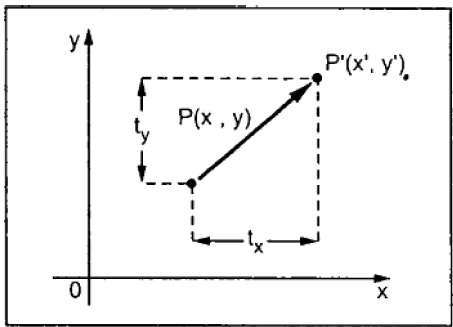
Dalla figura sopra, puoi scriverlo:

X’ = X + t_x

Y’ = Y + t_y

La coppia (t _x , t _y ) è chiamata vettore di traslazione o vettore di spostamento. Le equazioni di cui sopra possono anche essere rappresentate utilizzando i vettori colonna.

$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $

Possiamo scriverlo come -

P’ = P + T

Rotazione

In rotazione, ruotiamo l'oggetto di un particolare angolo θ (theta) dalla sua origine. Dalla figura seguente, possiamo vedere che il punto P (X, Y) si trova all'angolo φ dalla coordinata X orizzontale con distanza r dall'origine.

Supponiamo che tu voglia ruotarlo dell'angolo θ. Dopo averlo ruotato in una nuova posizione, otterrai un nuovo punto P '(X', Y ').

Usando la trigonometrica standard, la coordinata originale del punto P (X, Y) può essere rappresentata come -

$ X = r \, cos \, \ phi ...... (1) $

$ Y = r \, sin \, \ phi ...... (2) $

Allo stesso modo possiamo rappresentare il punto P '(X', Y ') come -

$ {x} '= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: - \: r \ : sin \: \ phi \: sin \: \ theta ....... (3) $

$ {y} '= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : sin \: \ phi \: cos \: \ theta ....... (4) $

Sostituendo l'equazione (1) e (2) in (3) e (4) rispettivamente, otterremo

$ {x} '= x \: cos \: \ theta - \: y \: sin \: \ theta $

$ {y} '= x \: sin \: \ theta + \: y \: cos \: \ theta $

Rappresentando l'equazione di cui sopra in forma di matrice,

$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} OR $$

P '= P. R

Dove R è la matrice di rotazione

$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$

L'angolo di rotazione può essere positivo e negativo.

Per un angolo di rotazione positivo, possiamo usare la matrice di rotazione sopra. Tuttavia, per la rotazione dell'angolo negativo, la matrice cambierà come mostrato di seguito -

$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$

$$ = \ begin {bmatrice} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ because cos (- \ theta) = cos \ theta \; e \; sin (- \ theta) = −sin \ theta \ right) $$

Ridimensionamento

Per modificare le dimensioni di un oggetto, viene utilizzata la trasformazione in scala. Nel processo di ridimensionamento, espandi o comprimi le dimensioni dell'oggetto. Il ridimensionamento può essere ottenuto moltiplicando le coordinate originali dell'oggetto per il fattore di scala per ottenere il risultato desiderato.

Supponiamo che le coordinate originali siano (X, Y), i fattori di scala siano (S _X , S _Y ) e le coordinate prodotte siano (X ', Y'). Questo può essere rappresentato matematicamente come mostrato di seguito:

X' = X . S_X and Y' = Y . S_Y

Il fattore di scala S _X , S _Y scala l'oggetto rispettivamente in direzione X e Y. Le equazioni di cui sopra possono anche essere rappresentate in forma di matrice come di seguito -

$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$

P’ = P . S

Dove S è la matrice di scala. Il processo di ridimensionamento è mostrato nella figura seguente.

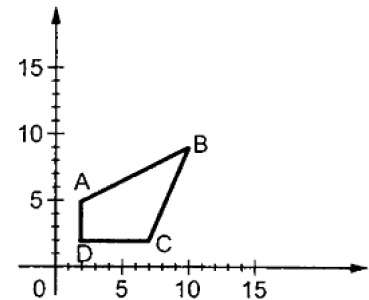
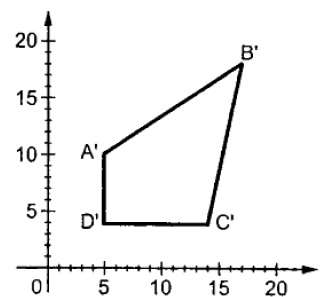
Se forniamo valori inferiori a 1 al fattore di scala S, possiamo ridurre la dimensione dell'oggetto. Se forniamo valori maggiori di 1, possiamo aumentare la dimensione dell'oggetto.

Riflessione

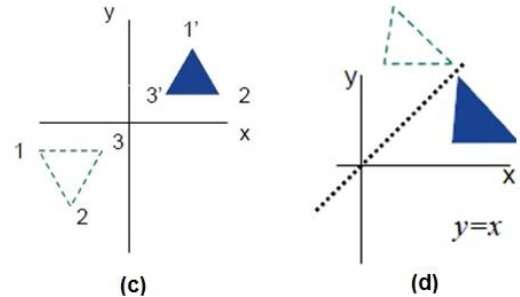
Il riflesso è l'immagine speculare dell'oggetto originale. In altre parole, possiamo dire che è un'operazione di rotazione di 180 °. Nella trasformazione della riflessione, la dimensione dell'oggetto non cambia.

Le figure seguenti mostrano le riflessioni rispetto agli assi X e Y e rispetto all'origine rispettivamente.

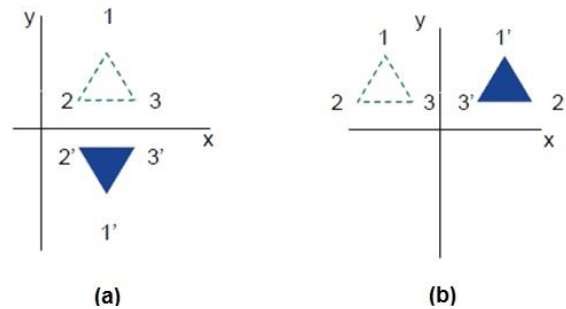
Shear

Una trasformazione che inclina la forma di un oggetto è chiamata trasformazione di taglio. Esistono due trasformazioni di taglioX-Shear e Y-Shear. Uno sposta i valori delle coordinate X e l'altro sposta i valori delle coordinate Y. Però; in entrambi i casi solo una coordinata cambia le sue coordinate e l'altra conserva i suoi valori. La tosatura è anche definita comeSkewing.

X-Shear

X-Shear preserva la coordinata Y e vengono apportate modifiche alle coordinate X, il che fa sì che le linee verticali si inclinino a destra oa sinistra come mostrato nella figura sotto.

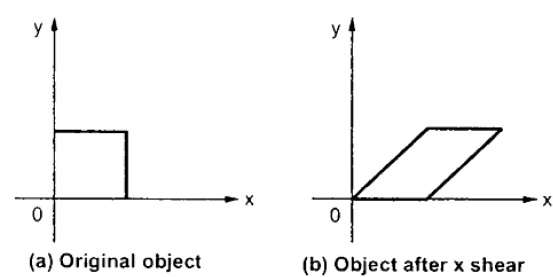
La matrice di trasformazione per X-Shear può essere rappresentata come:

$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$

Y '= Y + Sh _y . X

X '= X

Y-Shear

Y-Shear preserva le coordinate X e cambia le coordinate Y che fa sì che le linee orizzontali si trasformino in linee che si inclinano verso l'alto o verso il basso come mostrato nella figura seguente.

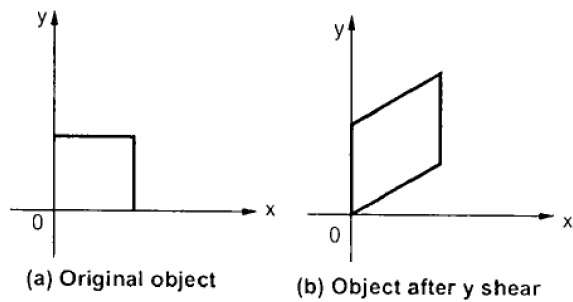
Lo Y-Shear può essere rappresentato in matrice da come -

$$ Y_ {sh} \ begin {bmatrix} 1 & 0 & 0 \\ shy & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$

X '= X + Sh _x . Y

Y '= Y

Trasformazione composita

Se una trasformazione del piano T1 è seguita da una seconda trasformazione del piano T2, allora il risultato stesso può essere rappresentato da un'unica trasformazione T che è la composizione di T1 e T2 presa in quell'ordine. Questo è scritto come T = T1 ∙ T2.

La trasformazione composita può essere ottenuta concatenando le matrici di trasformazione per ottenere una matrice di trasformazione combinata.

Una matrice combinata -

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

Dove [Ti] è una qualsiasi combinazione di

Translation
Scaling
Shearing
Rotation
Reflection

Il cambiamento nell'ordine di trasformazione porterebbe a risultati diversi, poiché in generale la moltiplicazione di matrici non è cumulativa, cioè [A]. [B] ≠ [B]. [A] e l'ordine di moltiplicazione. Lo scopo fondamentale della composizione delle trasformazioni è ottenere efficienza applicando una singola trasformazione composta a un punto, piuttosto che applicare una serie di trasformazioni, una dopo l'altra.

Ad esempio, per ruotare un oggetto su un punto arbitrario (X _p , Y _p ), dobbiamo eseguire tre passaggi:

Trasla il punto (X _p , Y _p ) all'origine.
Ruotalo intorno all'origine.
Infine, riporta il centro di rotazione dove apparteneva.