Computer Graphics - Guida rapida
La computer grafica è un'arte di disegnare immagini sugli schermi dei computer con l'aiuto della programmazione. Comporta calcoli, creazione e manipolazione di dati. In altre parole, possiamo dire che la computer grafica è uno strumento di rendering per la generazione e la manipolazione di immagini.
Tubo a raggi catodici
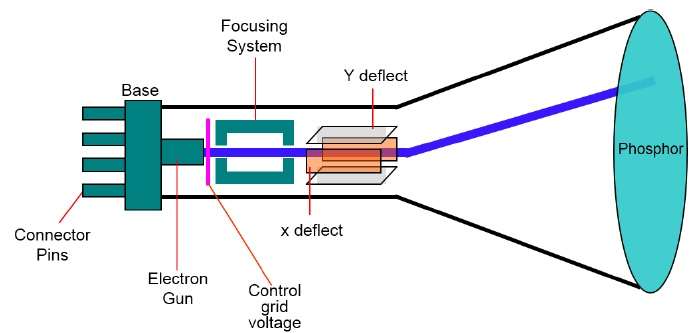
Il dispositivo di output principale in un sistema grafico è il monitor video. L'elemento principale di un monitor video è ilCathode Ray Tube (CRT), mostrato nell'illustrazione seguente.
Il funzionamento di CRT è molto semplice:
Il cannone elettronico emette un fascio di elettroni (raggi catodici).
Il fascio di elettroni passa attraverso sistemi di focalizzazione e deflessione che lo dirigono verso posizioni specificate sullo schermo rivestito di fosforo.
Quando il raggio colpisce lo schermo, il fosforo emette un piccolo punto di luce in ogni posizione a cui entra in contatto il fascio di elettroni.
Ridisegna l'immagine dirigendo rapidamente il fascio di elettroni sugli stessi punti dello schermo.
Ci sono due modi (scansione casuale e scansione raster) con cui possiamo visualizzare un oggetto sullo schermo.
Scansione raster
In un sistema di scansione raster, il fascio di elettroni viene spostato sullo schermo, una riga alla volta dall'alto verso il basso. Quando il fascio di elettroni si sposta su ciascuna riga, l'intensità del fascio viene attivata e disattivata per creare uno schema di punti illuminati.
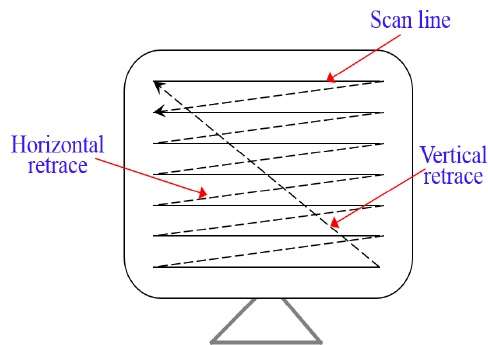
La definizione dell'immagine è archiviata nell'area di memoria denominata Refresh Buffer o Frame Buffer. Questa area di memoria contiene l'insieme dei valori di intensità per tutti i punti dello schermo. I valori di intensità memorizzati vengono quindi recuperati dal buffer di aggiornamento e "disegnati" sullo schermo una riga (linea di scansione) alla volta come mostrato nell'illustrazione seguente.
Ogni punto dello schermo viene indicato come un file pixel (picture element) o pel. Alla fine di ogni linea di scansione, il fascio di elettroni ritorna sul lato sinistro dello schermo per iniziare a visualizzare la linea di scansione successiva.
Scansione casuale (scansione vettoriale)
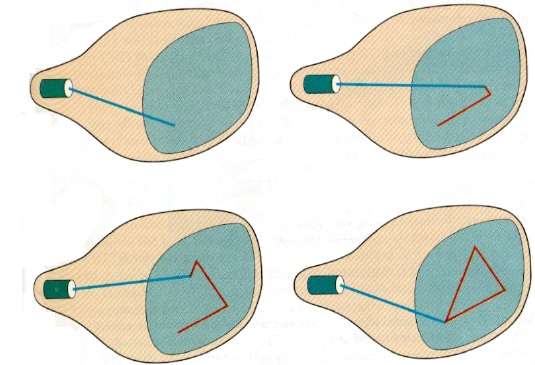
In questa tecnica, il fascio di elettroni è diretto solo verso la parte dello schermo dove deve essere disegnata l'immagine invece di scansionare da sinistra a destra e dall'alto verso il basso come nella scansione raster. È anche chiamatovector display, stroke-writing display, o calligraphic display.
La definizione dell'immagine viene memorizzata come un insieme di comandi di disegno di linee in un'area di memoria denominata refresh display file. Per visualizzare un'immagine specifica, il sistema passa in rassegna la serie di comandi nel file di visualizzazione, disegnando a turno ciascuna linea del componente. Dopo che tutti i comandi di disegno di linea sono stati elaborati, il sistema torna al primo comando di linea nell'elenco.
I display a scansione casuale sono progettati per disegnare tutte le linee componenti di un'immagine da 30 a 60 volte al secondo.
Applicazione della computer grafica
Computer Graphics ha numerose applicazioni, alcune delle quali sono elencate di seguito:
Computer graphics user interfaces (GUIs) - Un paradigma grafico orientato al mouse che consente all'utente di interagire con un computer.
Business presentation graphics - "Un'immagine vale più di mille parole".
Cartography - Disegnare mappe.
Weather Maps - Mappatura in tempo reale, rappresentazioni simboliche.
Satellite Imaging - Immagini geodetiche.
Photo Enhancement - Affilatura foto sfocate.
Medical imaging - MRI, TAC, ecc. - Esame interno non invasivo.
Engineering drawings - meccanico, elettrico, civile, ecc. - Sostituzione dei progetti del passato.
Typography - L'uso di immagini dei personaggi nell'editoria - che sostituisce il tipo duro del passato.
Architecture - Piani di costruzione, schizzi esterni - in sostituzione dei progetti e dei disegni a mano del passato.
Art - I computer forniscono un nuovo mezzo per gli artisti.
Training - Simulatori di volo, istruzioni assistite da computer, ecc.
Entertainment - Film e giochi.
Simulation and modeling - Sostituzione della modellazione fisica e degli enactment
Una linea collega due punti. È un elemento di base nella grafica. Per disegnare una linea, hai bisogno di due punti tra i quali puoi disegnare una linea. Nei seguenti tre algoritmi, ci riferiamo a un punto di linea come$X_{0}, Y_{0}$ e il secondo punto di linea come $X_{1}, Y_{1}$.
Algoritmo DDA
L'algoritmo dell'analizzatore differenziale digitale (DDA) è il semplice algoritmo di generazione della linea che viene spiegato passo dopo passo qui.
Step 1 - Ottieni l'input di due punti finali $(X_{0}, Y_{0})$ e $(X_{1}, Y_{1})$.
Step 2 - Calcola la differenza tra due punti finali.
dx = X1 - X0
dy = Y1 - Y0Step 3- In base alla differenza calcolata nel passaggio 2, è necessario identificare il numero di passaggi per inserire pixel. Se dx> dy, allora hai bisogno di più passaggi in coordinata x; altrimenti in coordinata y.
if (absolute(dx) > absolute(dy))
Steps = absolute(dx);
else
Steps = absolute(dy);Step 4 - Calcola l'incremento in coordinata x e coordinata y.
Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;Step 5 - Metti il pixel incrementando con successo le coordinate xey di conseguenza e completa il disegno della linea.
for(int v=0; v < Steps; v++)
{
x = x + Xincrement;
y = y + Yincrement;
putpixel(Round(x), Round(y));
}Generazione di linee di Bresenham
L'algoritmo di Bresenham è un altro algoritmo di conversione della scansione incrementale. Il grande vantaggio di questo algoritmo è che utilizza solo calcoli interi. Spostandoti sull'asse x in intervalli di unità e ad ogni passaggio scegli tra due diverse coordinate y.
Ad esempio, come mostrato nell'illustrazione seguente, dalla posizione (2, 3) è necessario scegliere tra (3, 3) e (3, 4). Vorresti il punto più vicino alla linea originale.
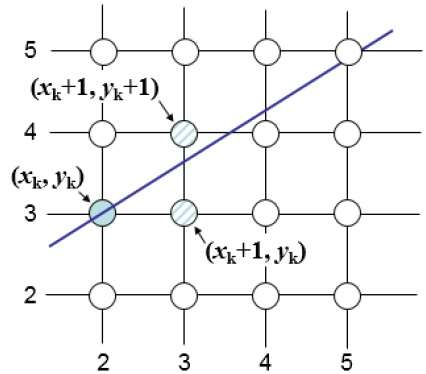
Alla posizione del campione $X_{k}+1,$ le separazioni verticali dalla linea matematica sono etichettate come $d_{upper}$ e $d_{lower}$.
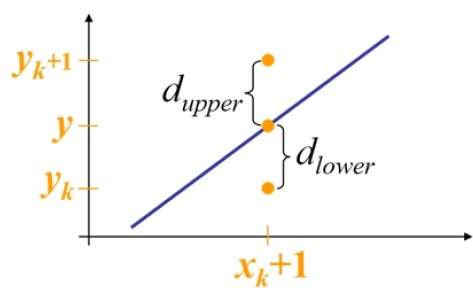
Dall'illustrazione sopra, la coordinata y sulla linea matematica in $x_{k}+1$ è -
Y = m ($X_{k}$+1) + b
Così, $d_{upper}$ e $d_{lower}$ sono dati come segue:
$$d_{lower} = y-y_{k}$$
$$= m(X_{k} + 1) + b - Y_{k}$$
e
$$d_{upper} = (y_{k} + 1) - y$$
$= Y_{k} + 1 - m (X_{k} + 1) - b$
Puoi usarli per prendere una decisione semplice su quale pixel è più vicino alla linea matematica. Questa semplice decisione si basa sulla differenza tra le due posizioni dei pixel.
$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$
Sostituiamo m con dy / dx dove dx e dy sono le differenze tra i punti finali.
$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$
$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$
$$ = 2dy.x_{k} - 2dx.y_{k} + C$$
Quindi, un parametro decisionale $P_{k}$poiché il k- esimo passo lungo una linea è dato da -
$$p_{k} = dx(d_{lower} - d_{upper})$$
$$ = 2dy.x_{k} - 2dx.y_{k} + C$$
Il segno del parametro decisionale $P_{k}$ è uguale a quello di $d_{lower} - d_{upper}$.
Se $p_{k}$ è negativo, quindi scegli il pixel inferiore, altrimenti scegli il pixel superiore.
Ricorda, le modifiche alle coordinate avvengono lungo l'asse x in incrementi di unità, quindi puoi fare tutto con calcoli interi. Al passo k + 1, il parametro di decisione è dato come -
$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$
Sottraendo $p_{k}$ da questo otteniamo -
$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$
Ma, $x_{k+1}$ equivale a $x_{k+1}$. Quindi ...
$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$
Dove, $Y_{k+1} – Y_{k}$ è 0 o 1 a seconda del segno di $P_{k}$.
Il primo parametro decisionale $p_{0}$ è valutato a $(x_{0}, y_{0})$ è dato come -
$$p_{0} = 2dy - dx$$
Ora, tenendo presente tutti i punti e i calcoli di cui sopra, ecco l'algoritmo di Bresenham per la pendenza m <1 -
Step 1 - Immettere i due punti finali della linea, memorizzando il punto finale sinistro in $(x_{0}, y_{0})$.
Step 2 - Traccia il punto $(x_{0}, y_{0})$.
Step 3 - Calcola le costanti dx, dy, 2dy e (2dy - 2dx) e ottieni il primo valore per il parametro decisionale come -
$$p_{0} = 2dy - dx$$
Step 4 - A ciascuno $X_{k}$ lungo la linea, a partire da k = 0, eseguire il seguente test:
Se $p_{k}$ <0, il punto successivo da tracciare è $(x_{k}+1, y_{k})$ e
$$p_{k+1} = p_{k} + 2dy$$ Altrimenti,
$$(x_{k}, y_{k}+1)$$
$$p_{k+1} = p_{k} + 2dy - 2dx$$
Step 5 - Ripetere il passaggio 4 (dx - 1) volte.
Per m> 1, scopri se devi aumentare x incrementando y ogni volta.
Dopo aver risolto, l'equazione per il parametro decisionale $P_{k}$ sarà molto simile, solo la x e la y nell'equazione verranno scambiate.
Algoritmo del punto medio
L'algoritmo del punto medio è dovuto a Bresenham che è stato modificato da Pitteway e Van Aken. Supponiamo di aver già messo il punto P alla coordinata (x, y) e che la pendenza della linea sia 0 ≤ k ≤ 1 come mostrato nell'illustrazione seguente.
Ora devi decidere se mettere il punto successivo in E o N. Questo può essere scelto identificando il punto di intersezione Q più vicino al punto N o E. Se il punto di intersezione Q è più vicino al punto N allora N è considerato come il punto successivo; altrimenti E.
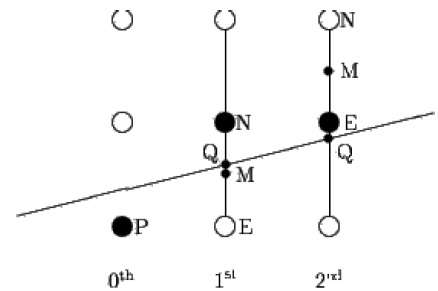
Per determinarlo, calcolare prima il punto medio M (x + 1, y + ½). Se il punto di intersezione Q della linea con la linea verticale che collega E e N è sotto M, allora prendi E come punto successivo; altrimenti prendi N come punto successivo.
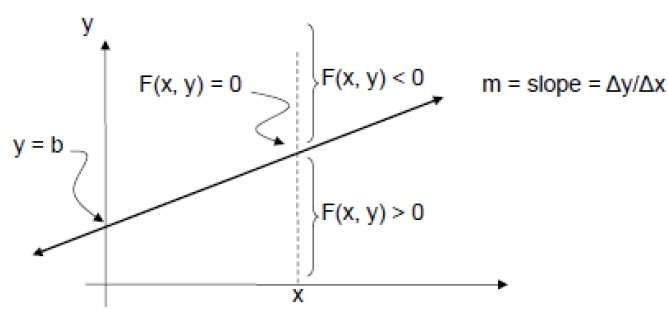
Per verificarlo, dobbiamo considerare l'equazione implicita -
F (x, y) = mx + b - y
Per m positivo in un dato X,
- Se y è sulla riga, allora F (x, y) = 0
- Se y è sopra la linea, allora F (x, y) <0
- Se y è sotto la linea, allora F (x, y)> 0
Disegnare un cerchio sullo schermo è un po 'complesso che disegnare una linea. Esistono due algoritmi popolari per generare un cerchio:Bresenham’s Algorithm e Midpoint Circle Algorithm. Questi algoritmi si basano sull'idea di determinare i successivi punti necessari per disegnare il cerchio. Parliamo in dettaglio degli algoritmi -
L'equazione del cerchio è $X^{2} + Y^{2} = r^{2},$ dove r è il raggio.
Algoritmo di Bresenham
Non è possibile visualizzare un arco continuo sulla visualizzazione raster. Invece, dobbiamo scegliere la posizione del pixel più vicina per completare l'arco.
Dalla seguente illustrazione, puoi vedere che abbiamo messo il pixel nella posizione (X, Y) e ora dobbiamo decidere dove mettere il pixel successivo - in N (X + 1, Y) o in S (X + 1, Y-1).
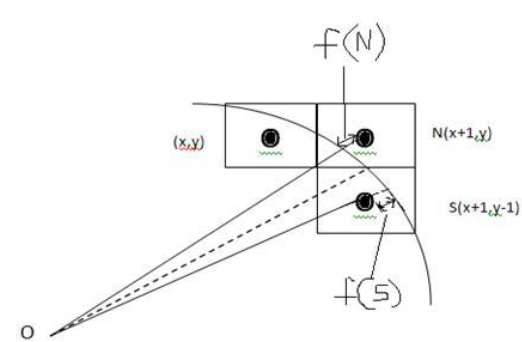
Questo può essere deciso dal parametro di decisione d.
- Se d <= 0, allora N (X + 1, Y) deve essere scelto come pixel successivo.
- Se d> 0, allora S (X + 1, Y-1) deve essere scelto come pixel successivo.
Algoritmo
Step 1- Ottieni le coordinate del centro del cerchio e del raggio e memorizzale rispettivamente in x, y e R. Porre P = 0 e Q = R.
Step 2 - Impostare il parametro di decisione D = 3 - 2R.
Step 3 - Ripetere il passaggio 8 mentre P ≤ Q.
Step 4 - Chiama Disegna cerchio (X, Y, P, Q).
Step 5 - Incrementa il valore di P.
Step 6 - Se D <0 allora D = D + 4P + 6.
Step 7 - Else Set R = R - 1, D = D + 4 (PQ) + 10.
Step 8 - Chiama Disegna cerchio (X, Y, P, Q).
Draw Circle Method(X, Y, P, Q).
Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).Algoritmo del punto medio
Step 1 - Raggio di input r e il centro del cerchio $(x_{c,} y_{c})$ e ottenere il primo punto sulla circonferenza del cerchio centrato sull'origine come
(x0, y0) = (0, r)Step 2 - Calcola il valore iniziale del parametro decisionale come
$P_{0}$ = 5/4 - r (Vedere la seguente descrizione per la semplificazione di questa equazione.)
f(x, y) = x2 + y2 - r2 = 0
f(xi - 1/2 + e, yi + 1)
= (xi - 1/2 + e)2 + (yi + 1)2 - r2
= (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
= f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0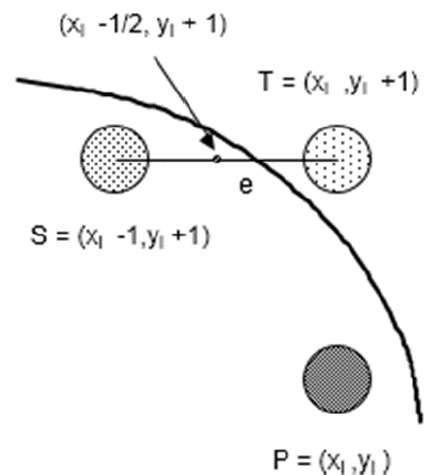
Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,
If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1 = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
= di - 2(xi - 1) + 2(yi + 1) + 1
= di + 2(yi + 1 - xi + 1) + 1
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
di+1 = f(xi - 1/2, yi + 1 + 1)
= di + 2yi+1 + 1
The initial value of di is
d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
= 5/4 - r {1-r can be used if r is an integer}
When point S = (xi - 1, yi + 1) is chosen then
di+1 = di + -2xi+1 + 2yi+1 + 1
When point T = (xi, yi + 1) is chosen then
di+1 = di + 2yi+1 + 1Step 3 - A ciascuno $X_{K}$ posizione a partire da K = 0, eseguire il seguente test:
If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
PK+1 = PK + 2XK+1 + 1
Else
PK+1 = PK + 2XK+1 + 1 – 2YK+1
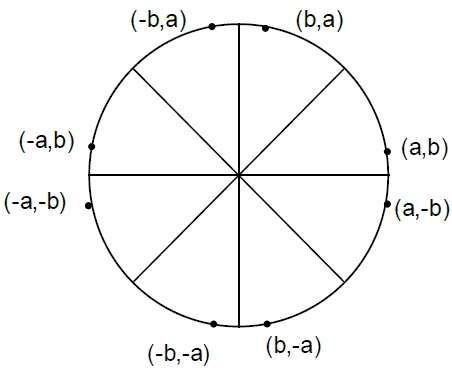
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.Step 4 - Determina i punti di simmetria in altri sette ottanti.
Step 5 - Spostare ogni posizione del pixel calcolato (X, Y) sul percorso circolare centrato su $(X_{C,} Y_{C})$ e traccia i valori delle coordinate.
X = X + XC, Y = Y + YCStep 6 - Ripetere i passaggi da 3 a 5 finché X> = Y.
Polygon è un elenco ordinato di vertici come mostrato nella figura seguente. Per riempire poligoni con colori particolari, è necessario determinare i pixel che cadono sul bordo del poligono e quelli che cadono all'interno del poligono. In questo capitolo vedremo come riempire i poligoni usando tecniche differenti.

Algoritmo della linea di scansione
Questo algoritmo funziona intersecando la linea di scansione con i bordi del poligono e riempie il poligono tra coppie di intersezioni. I passaggi seguenti illustrano come funziona questo algoritmo.
Step 1 - Trova Ymin e Ymax dal poligono dato.
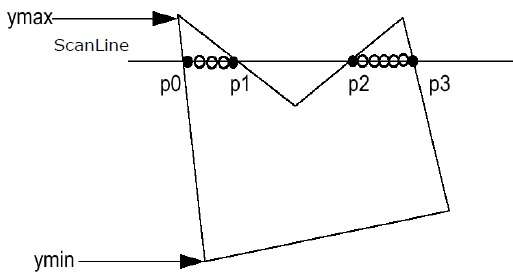
Step 2- ScanLine si interseca con ogni bordo del poligono da Ymin a Ymax. Assegna un nome a ciascun punto di intersezione del poligono. Secondo la figura mostrata sopra, sono denominati p0, p1, p2, p3.
Step 3 - Ordina il punto di intersezione nell'ordine crescente della coordinata X cioè (p0, p1), (p1, p2) e (p2, p3).
Step 4 - Riempi tutte quelle coppie di coordinate che si trovano all'interno di poligoni e ignora le coppie alternative.
Algoritmo Flood Fill
A volte ci imbattiamo in un oggetto in cui vogliamo riempire l'area e il suo confine con colori diversi. Possiamo dipingere tali oggetti con un colore interno specificato invece di cercare un colore di contorno particolare come nell'algoritmo di riempimento del contorno.
Invece di fare affidamento sul contorno dell'oggetto, si basa sul colore di riempimento. In altre parole, sostituisce il colore interno dell'oggetto con il colore di riempimento. Quando non esistono più pixel del colore interno originale, l'algoritmo è completato.
Ancora una volta, questo algoritmo si basa sul metodo Four-connect o Eight-connect per riempire i pixel. Ma invece di cercare il colore del contorno, cerca tutti i pixel adiacenti che fanno parte dell'interno.
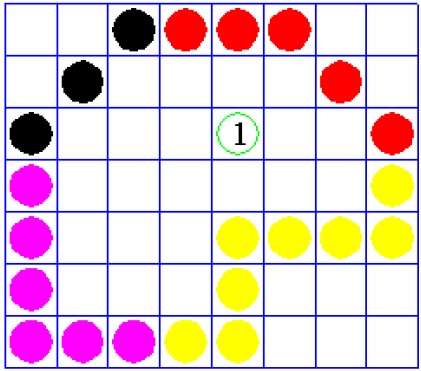
Algoritmo di riempimento del confine
L'algoritmo di riempimento del confine funziona come il suo nome. Questo algoritmo seleziona un punto all'interno di un oggetto e inizia a riempirsi fino a quando non raggiunge il confine dell'oggetto. Il colore del contorno e il colore che riempiamo dovrebbero essere diversi affinché questo algoritmo funzioni.
In questo algoritmo, assumiamo che il colore del contorno sia lo stesso per l'intero oggetto. L'algoritmo di riempimento del contorno può essere implementato da 4 pixel collegati o 8 pixel collegati.
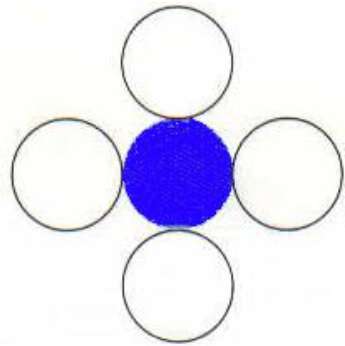
4-Connected Polygon
In questa tecnica vengono utilizzati 4 pixel collegati come mostrato in figura. Mettiamo i pixel sopra, sotto, a destra ea sinistra dei pixel attuali e questo processo continuerà fino a quando non troveremo un bordo con un colore diverso.
Algoritmo
Step 1 - Inizializza il valore di seed point (seedx, seedy), fcolor e dcol.
Step 2 - Definisci i valori limite del poligono.
Step 3 - Controlla se il punto di partenza corrente è del colore predefinito, quindi ripeti i passaggi 4 e 5 fino a raggiungere i pixel di confine.
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 - Cambia il colore predefinito con il colore di riempimento nel punto di partenza.
setPixel(seedx, seedy, fcol)Step 5 - Seguire ricorsivamente la procedura con quattro punti di vicinato.
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 - Esci
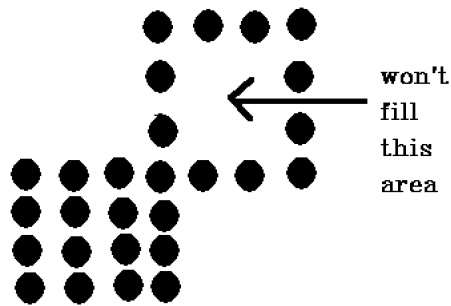
C'è un problema con questa tecnica. Considera il caso come mostrato di seguito in cui abbiamo cercato di riempire l'intera regione. L'immagine è riempita solo parzialmente. In questi casi, non è possibile utilizzare la tecnica dei 4 pixel collegati.
8-Connected Polygon
In questa tecnica vengono utilizzati 8 pixel collegati come mostrato in figura. Stiamo mettendo i pixel sopra, sotto, sul lato destro e sinistro dei pixel attuali come stavamo facendo nella tecnica a 4 connessioni.
Oltre a questo, stiamo anche mettendo i pixel in diagonale in modo che l'intera area del pixel corrente sia coperta. Questo processo continuerà fino a quando non troviamo un confine con un colore diverso.

Algoritmo
Step 1 - Inizializza il valore di seed point (seedx, seedy), fcolor e dcol.
Step 2 - Definisci i valori limite del poligono.
Step 3 - Controlla se il punto di partenza corrente è del colore predefinito, quindi ripeti i passaggi 4 e 5 fino a raggiungere i pixel di confine
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 - Cambia il colore predefinito con il colore di riempimento nel punto di partenza.
setPixel(seedx, seedy, fcol)Step 5 - Seguire ricorsivamente la procedura con quattro punti di vicinato
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 - Esci
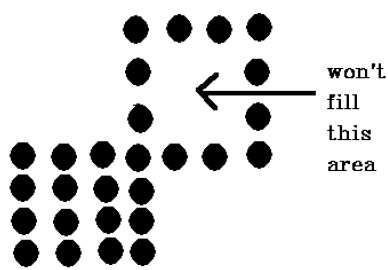
La tecnica dei pixel collegati a 4 non è riuscita a riempire l'area come indicato nella figura seguente, cosa che non avverrà con la tecnica dei pixel collegati a 8.
Test interno-esterno
Questo metodo è noto anche come counting number method. Durante il riempimento di un oggetto, spesso abbiamo bisogno di identificare se un punto particolare si trova all'interno o all'esterno dell'oggetto. Esistono due metodi con cui possiamo identificare se un punto particolare è all'interno di un oggetto o all'esterno.
- Regola dispari-pari
- Regola del numero di avvolgimento diverso da zero
Regola dispari-pari
In questa tecnica, contiamo il bordo che attraversa la linea da qualsiasi punto (x, y) all'infinito. Se il numero di interazioni è dispari, il punto (x, y) è un punto interno. Se il numero di interazioni è pari, il punto (x, y) è un punto esterno. Ecco l'esempio per darti un'idea chiara:
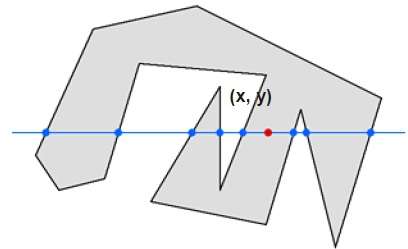
Dalla figura sopra, possiamo vedere che dal punto (x, y), il numero di punti di interazione sul lato sinistro è 5 e sul lato destro è 3. Quindi il numero totale di punti di interazione è 8, che è dispari . Quindi, il punto è considerato all'interno dell'oggetto.
Regola del numero di avvolgimento diverso da zero
Questo metodo viene utilizzato anche con i poligoni semplici per verificare che il punto specificato sia interno o meno. Può essere capito semplicemente con l'aiuto di uno spillo e un elastico. Fissare il perno su uno dei bordi del poligono e legare l'elastico in esso e quindi allungare l'elastico lungo i bordi del poligono.
Quando tutti i bordi del poligono sono coperti dall'elastico, controlla il perno che è stato fissato nel punto da testare. Se troviamo almeno un vento nel punto consideralo all'interno del poligono, altrimenti possiamo dire che il punto non è all'interno del poligono.
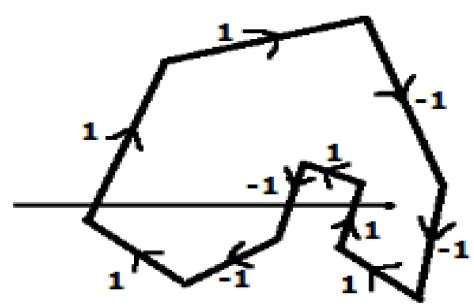
In un altro metodo alternativo, date le direzioni a tutti i bordi del poligono. Disegna una linea di scansione dal punto da testare verso l'estrema sinistra della direzione X.
Assegna il valore 1 a tutti i bordi che stanno andando verso l'alto e tutti gli altri -1 come valori di direzione.
Verificare i valori della direzione del bordo da cui passa la linea di scansione e sommarli.
Se la somma totale di questo valore di direzione è diverso da zero, questo punto da verificare è un interior point, altrimenti è un file exterior point.
Nella figura sopra, sommiamo i valori di direzione da cui passa la linea di scansione, quindi il totale è 1 - 1 + 1 = 1; che è diverso da zero. Quindi si dice che il punto sia un punto interiore.
L'uso principale del ritaglio nella grafica computerizzata è rimuovere oggetti, linee o segmenti di linea che si trovano al di fuori del riquadro di visualizzazione. La trasformazione della visualizzazione è insensibile alla posizione dei punti rispetto al volume di visualizzazione, in particolare quei punti dietro lo spettatore, ed è necessario rimuovere questi punti prima di generare la visualizzazione.
Punto di ritaglio
Ritagliare un punto da una data finestra è molto semplice. Considera la figura seguente, dove il rettangolo indica la finestra. Il ritaglio del punto ci dice se il punto dato (X, Y) si trova all'interno della finestra data oppure no; e decide se useremo le coordinate minime e massime della finestra.
La coordinata X del punto dato è all'interno della finestra, se X si trova tra Wx1 ≤ X ≤ Wx2. Allo stesso modo, la coordinata Y del punto dato è all'interno della finestra, se Y si trova tra Wy1 ≤ Y ≤ Wy2.

Ritaglio di linea
Il concetto di ritaglio di linea è lo stesso del ritaglio di punti. Nel ritaglio di linea, taglieremo la porzione di linea che è fuori dalla finestra e manterremo solo la parte che si trova all'interno della finestra.
Ritagli di linea Cohen-Sutherland
Questo algoritmo utilizza la finestra di ritaglio come mostrato nella figura seguente. La coordinata minima per la regione di ritaglio è$(XW_{min,} YW_{min})$ e la coordinata massima per la regione di ritaglio è $(XW_{max,} YW_{max})$.
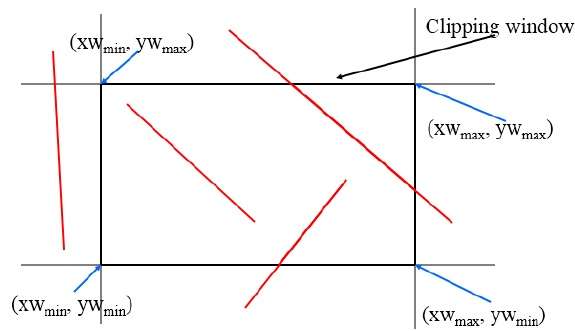
Useremo 4 bit per dividere l'intera regione. Questi 4 bit rappresentano la parte superiore, inferiore, destra e sinistra della regione, come mostrato nella figura seguente. Qui, ilTOP e LEFT bit è impostato a 1 perché è il TOP-LEFT angolo.
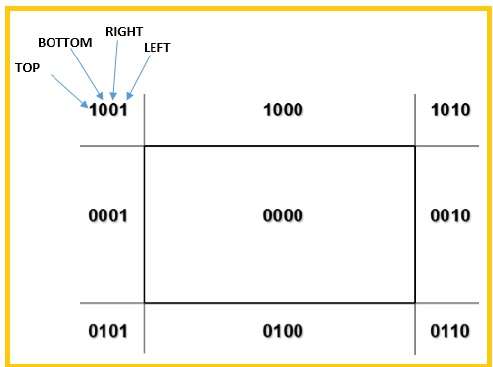
Ci sono 3 possibilità per la linea:
La riga può essere completamente all'interno della finestra (questa riga dovrebbe essere accettata).
La linea può essere completamente al di fuori della finestra (questa linea verrà completamente rimossa dalla regione).
La linea può essere parzialmente all'interno della finestra (troveremo il punto di intersezione e disegneremo solo quella porzione di linea che si trova all'interno della regione).
Algoritmo
Step 1 - Assegna un codice regionale per ogni endpoint.
Step 2 - Se entrambi gli endpoint hanno un codice regione 0000 quindi accetta questa riga.
Step 3 - Altrimenti, esegui la logica ANDfunzionamento per entrambi i codici regionali.
Step 3.1 - Se il risultato non lo è 0000, quindi rifiuta la linea.
Step 3.2 - Altrimenti ti serve il ritaglio.
Step 3.2.1 - Scegli un punto finale della linea che è fuori dalla finestra.
Step 3.2.2 - Trova il punto di intersezione al confine della finestra (in base al codice regionale).
Step 3.2.3 - Sostituisci endpoint con il punto di intersezione e aggiorna il codice regione.
Step 3.2.4 - Ripetere il passaggio 2 fino a quando non troviamo una linea tagliata banalmente accettata o banalmente rifiutata.
Step 4 - Ripetere il passaggio 1 per altre righe.
Algoritmo di ritaglio della linea Cyrus-Beck
Questo algoritmo è più efficiente dell'algoritmo di Cohen-Sutherland. Utilizza la rappresentazione parametrica delle linee e semplici prodotti a punti.
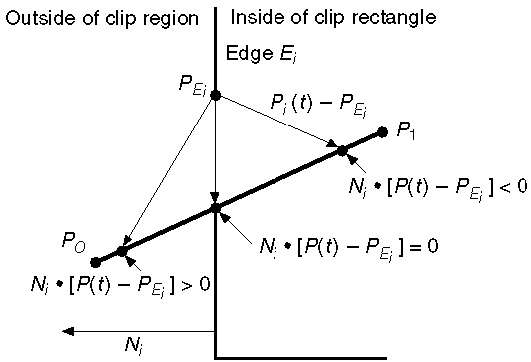
L'equazione parametrica della retta è -
P0P1:P(t) = P0 + t(P1-P0)Sia N i il bordo normale verso l'esterno E i . Ora scegli un punto arbitrario P Ei sul bordo E i quindi il prodotto scalare N i ∙ [P (t) - P Ei ] determina se il punto P (t) è "all'interno del bordo della clip" o "all'esterno" del bordo della clip o "Sul" bordo della clip.
Il punto P (t) è interno se N i . [P (t) - P Ei ] <0
Il punto P (t) è esterno se N i . [P (t) - P Ei ]> 0
Il punto P (t) è sul bordo se N i . [P (t) - P Ei ] = 0 (Punto di intersezione)
N i . [P (t) - P Ei ] = 0
N i . [P 0 + t (P 1 -P 0 ) - P Ei ] = 0 (Sostituendo P (t) con P 0 + t (P 1 -P 0 ))
N i . [P 0 - P Ei ] + N i .t [P 1 -P 0 ] = 0
N i . [P 0 - P Ei ] + N i ∙ tD = 0 (sostituendo D con [P 1 -P 0 ])
N i . [P 0 - P Ei ] = - N i ∙ tD
L'equazione per t diventa,
$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$
È valido per le seguenti condizioni:
- N i ≠ 0 (l'errore non può verificarsi)
- D ≠ 0 (P 1 ≠ P 0 )
- N i ∙ D ≠ 0 (P 0 P 1 non parallelo a E i )
Ritaglio di poligoni (algoritmo di Sutherland Hodgman)
Un poligono può anche essere ritagliato specificando la finestra di ritaglio. L'algoritmo di ritaglio del poligono di Sutherland Hodgeman viene utilizzato per il ritaglio del poligono. In questo algoritmo, tutti i vertici del poligono vengono ritagliati contro ogni bordo della finestra di ritaglio.
Prima il poligono viene ritagliato contro il bordo sinistro della finestra del poligono per ottenere nuovi vertici del poligono. Questi nuovi vertici vengono utilizzati per ritagliare il poligono contro il bordo destro, il bordo superiore, il bordo inferiore della finestra di ritaglio come mostrato nella figura seguente.
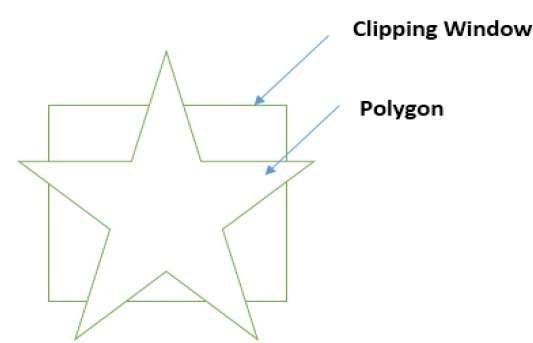
Durante l'elaborazione di un bordo di un poligono con una finestra di ritaglio, viene trovato un punto di intersezione se il bordo non è completamente all'interno della finestra di ritaglio e viene ritagliato un bordo parziale dal punto di intersezione al bordo esterno. Le figure seguenti mostrano i ritagli del bordo sinistro, destro, superiore e inferiore -
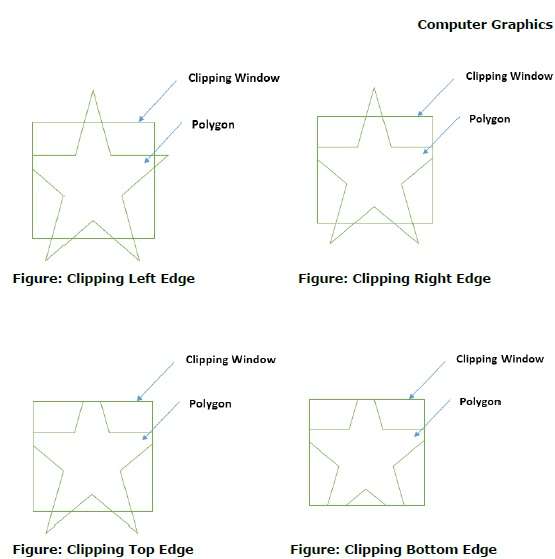
Ritaglio di testo
Diverse tecniche vengono utilizzate per fornire il ritaglio del testo in una computer grafica. Dipende dai metodi utilizzati per generare i caratteri e dai requisiti di una particolare applicazione. Esistono tre metodi per il ritaglio del testo elencati di seguito:
- Ritaglio di stringa tutto o nessuno
- Ritaglio di caratteri tutto o nessuno
- Ritaglio del testo
La figura seguente mostra il ritaglio di stringhe tutto o niente -
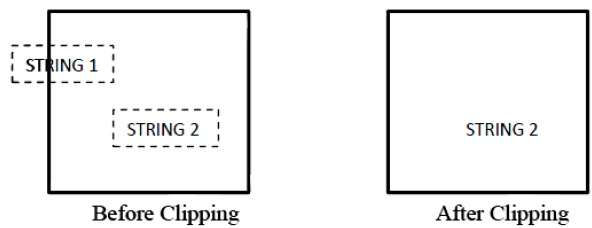
Nel metodo di clipping delle stringhe tutte o nessuna, manteniamo l'intera stringa o rifiutiamo l'intera stringa in base alla finestra di ritaglio. Come mostrato nella figura sopra, STRING2 è interamente all'interno della finestra di ritaglio, quindi lo teniamo e STRING1 essendo solo parzialmente all'interno della finestra, rifiutiamo.
La figura seguente mostra il ritaglio di tutti o nessuno dei caratteri:
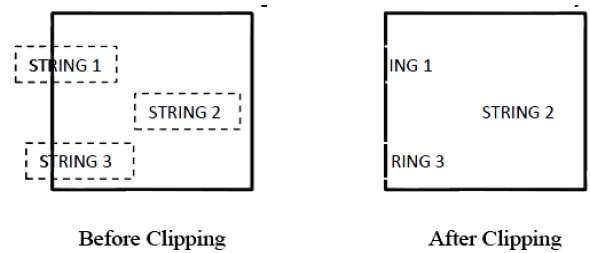
Questo metodo di ritaglio si basa sui caratteri anziché sull'intera stringa. In questo metodo, se la stringa è interamente all'interno della finestra di ritaglio, la manteniamo. Se è parzialmente fuori dalla finestra, allora -
Rifiuti solo la parte della stringa che si trova all'esterno
Se il carattere si trova sul confine della finestra di ritaglio, scartiamo l'intero carattere e conserviamo la stringa rimanente.
La figura seguente mostra il ritaglio del testo:
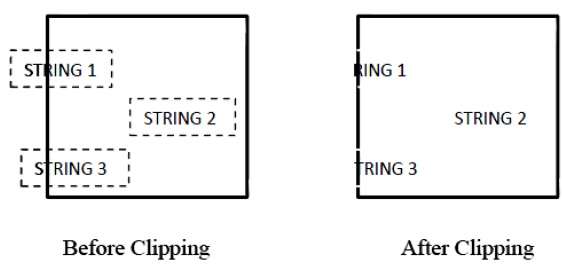
Questo metodo di ritaglio si basa sui caratteri anziché sull'intera stringa. In questo metodo, se la stringa è interamente all'interno della finestra di ritaglio, la manteniamo. Se è parzialmente fuori dalla finestra, allora
Rifiuti solo la parte di stringa che si trova all'esterno.
Se il carattere si trova sul confine della finestra di ritaglio, scartiamo solo quella porzione di carattere che si trova al di fuori della finestra di ritaglio.
Grafica bitmap
Una bitmap è una raccolta di pixel che descrive un'immagine. È un tipo di computer grafica che il computer utilizza per memorizzare e visualizzare le immagini. In questo tipo di grafica, le immagini vengono memorizzate bit per bit e quindi è denominata Bit-map graphics. Per una migliore comprensione, prendiamo in considerazione il seguente esempio in cui disegniamo una faccina sorridente utilizzando grafici bitmap.

Ora vedremo come questa faccina sorridente viene memorizzata un po 'alla volta nella computer grafica.
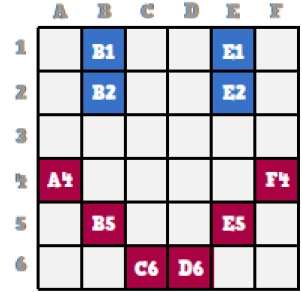
Osservando da vicino la faccina sorridente originale, possiamo vedere che ci sono due linee blu che sono rappresentate come B1, B2 e E1, E2 nella figura sopra.
Allo stesso modo, lo smiley viene rappresentato utilizzando i bit di combinazione di A4, B5, C6, D6, E5 e F4 rispettivamente.
I principali svantaggi della grafica bitmap sono:
Non è possibile ridimensionare l'immagine bitmap. Se provi a ridimensionare, i pixel diventano sfocati.
Le bitmap colorate possono essere molto grandi.
Trasformazione significa cambiare alcuni elementi grafici in qualcos'altro applicando delle regole. Possiamo avere vari tipi di trasformazioni come traslazione, scalatura su o giù, rotazione, inclinazione, ecc. Quando una trasformazione avviene su un piano 2D, si chiama trasformazione 2D.
Le trasformazioni giocano un ruolo importante nella computer grafica per riposizionare la grafica sullo schermo e cambiarne le dimensioni o l'orientamento.
Coordinate omogenee
Per eseguire una sequenza di trasformazione come la traslazione seguita da rotazione e ridimensionamento, dobbiamo seguire un processo sequenziale:
- Traduci le coordinate,
- Ruota le coordinate tradotte e poi
- Ridimensionare le coordinate ruotate per completare la trasformazione composita.
Per abbreviare questo processo, dobbiamo utilizzare la matrice di trasformazione 3 × 3 invece della matrice di trasformazione 2 × 2. Per convertire una matrice 2 × 2 in una matrice 3 × 3, dobbiamo aggiungere una coordinata fittizia extra W.
In questo modo, possiamo rappresentare il punto con 3 numeri invece di 2 numeri, che viene chiamato Homogenous Coordinatesistema. In questo sistema, possiamo rappresentare tutte le equazioni di trasformazione nella moltiplicazione di matrici. Qualsiasi punto cartesiano P (X, Y) può essere convertito in coordinate omogenee da P '(X h , Y h , h).
Traduzione
Una traduzione sposta un oggetto in una posizione diversa sullo schermo. È possibile tradurre un punto in 2D aggiungendo la coordinata di traslazione (t x , t y ) alla coordinata originale (X, Y) per ottenere la nuova coordinata (X ', Y').
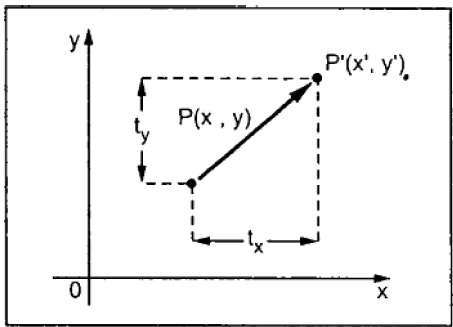
Dalla figura sopra, puoi scriverlo:
X’ = X + tx
Y’ = Y + ty
La coppia (t x , t y ) è chiamata vettore di traslazione o vettore di spostamento. Le equazioni di cui sopra possono anche essere rappresentate utilizzando i vettori colonna.
$P = \frac{[X]}{[Y]}$ p '= $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$
Possiamo scriverlo come -
P’ = P + T
Rotazione
In rotazione, ruotiamo l'oggetto di un particolare angolo θ (theta) dalla sua origine. Dalla figura seguente, possiamo vedere che il punto P (X, Y) si trova all'angolo φ dalla coordinata X orizzontale con distanza r dall'origine.
Supponiamo che tu voglia ruotarlo dell'angolo θ. Dopo averlo ruotato in una nuova posizione, otterrai un nuovo punto P '(X', Y ').

Usando la trigonometrica standard la coordinata originale del punto P (X, Y) può essere rappresentata come -
$X = r \, cos \, \phi ...... (1)$
$Y = r \, sin \, \phi ...... (2)$
Allo stesso modo possiamo rappresentare il punto P '(X', Y ') come -
${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$
${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$
Sostituendo l'equazione (1) e (2) in (3) e (4) rispettivamente, otterremo
${x}'= x \: cos \: \theta − \: y \: sin \: \theta $
${y}'= x \: sin \: \theta + \: y \: cos \: \theta $
Rappresentando l'equazione di cui sopra in forma di matrice,
$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$
P '= P ∙ R
Dove R è la matrice di rotazione
$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$
L'angolo di rotazione può essere positivo e negativo.
Per un angolo di rotazione positivo, possiamo usare la matrice di rotazione sopra. Tuttavia, per la rotazione dell'angolo negativo, la matrice cambierà come mostrato di seguito -
$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$
$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$
Ridimensionamento
Per modificare le dimensioni di un oggetto, viene utilizzata la trasformazione in scala. Nel processo di ridimensionamento, espandi o comprimi le dimensioni dell'oggetto. Il ridimensionamento può essere ottenuto moltiplicando le coordinate originali dell'oggetto per il fattore di scala per ottenere il risultato desiderato.
Supponiamo che le coordinate originali siano (X, Y), i fattori di scala siano (S X , S Y ) e le coordinate prodotte siano (X ', Y'). Questo può essere rappresentato matematicamente come mostrato di seguito:
X' = X . SX and Y' = Y . SY
Il fattore di scala S X , S Y scala l'oggetto rispettivamente in direzione X e Y. Le equazioni di cui sopra possono anche essere rappresentate in forma di matrice come di seguito -
$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$
O
P’ = P . S
Dove S è la matrice di scala. Il processo di ridimensionamento è mostrato nella figura seguente.
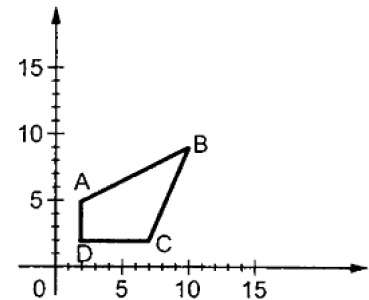
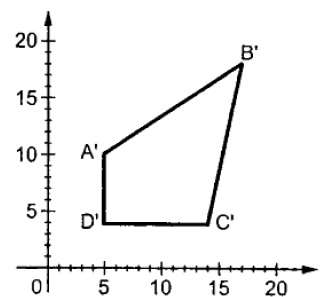
Se forniamo valori inferiori a 1 al fattore di scala S, possiamo ridurre la dimensione dell'oggetto. Se forniamo valori maggiori di 1, possiamo aumentare la dimensione dell'oggetto.
Riflessione
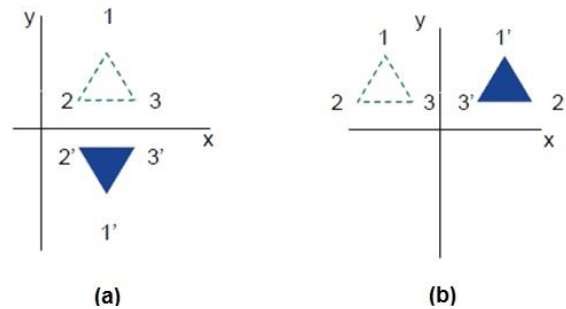
Il riflesso è l'immagine speculare dell'oggetto originale. In altre parole, possiamo dire che è un'operazione di rotazione di 180 °. Nella trasformazione della riflessione, la dimensione dell'oggetto non cambia.
Le figure seguenti mostrano le riflessioni rispetto agli assi X e Y e rispetto all'origine rispettivamente.
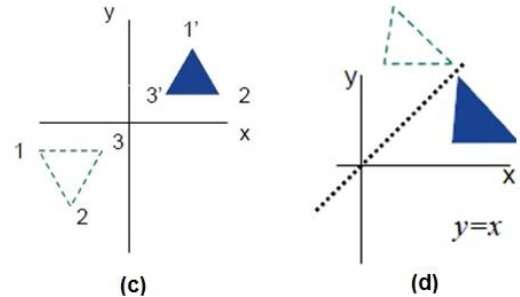
Shear
Una trasformazione che inclina la forma di un oggetto è chiamata trasformazione di taglio. Esistono due trasformazioni di taglioX-Shear e Y-Shear. Uno sposta i valori delle coordinate X e l'altro sposta i valori delle coordinate Y. Però; in entrambi i casi solo una coordinata cambia le sue coordinate e l'altra conserva i suoi valori. La tosatura è anche definita comeSkewing.
X-Shear
X-Shear preserva la coordinata Y e vengono apportate modifiche alle coordinate X, il che fa sì che le linee verticali si inclinino a destra oa sinistra come mostrato nella figura sotto.
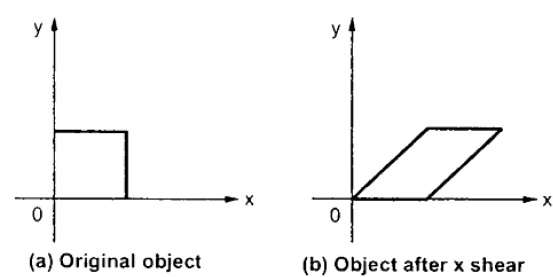
La matrice di trasformazione per X-Shear può essere rappresentata come:
$$X_{sh} = \begin{bmatrix} 1& shx& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$
Y '= Y + Sh y . X
X '= X
Y-Shear
Y-Shear preserva le coordinate X e cambia le coordinate Y che fa sì che le linee orizzontali si trasformino in linee che si inclinano verso l'alto o verso il basso come mostrato nella figura seguente.
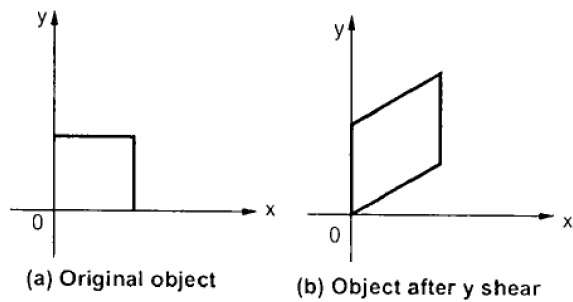
Y-Shear può essere rappresentato in matrice da come -
$$Y_{sh} \begin{bmatrix} 1& 0& 0\\ shy& 1& 0\\ 0& 0& 1 \end{bmatrix}$$
X '= X + Sh x . Y
Y '= Y
Trasformazione composita
Se una trasformazione del piano T1 è seguita da una seconda trasformazione del piano T2, allora il risultato stesso può essere rappresentato da un'unica trasformazione T che è la composizione di T1 e T2 presa in quell'ordine. Questo è scritto come T = T1 ∙ T2.
La trasformazione composita può essere ottenuta concatenando matrici di trasformazione per ottenere una matrice di trasformazione combinata.
Una matrice combinata -
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
Dove [Ti] è una qualsiasi combinazione di
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
Il cambiamento nell'ordine di trasformazione porterebbe a risultati diversi, poiché in generale la moltiplicazione di matrici non è cumulativa, cioè [A]. [B] ≠ [B]. [A] e l'ordine di moltiplicazione. Lo scopo fondamentale della composizione delle trasformazioni è ottenere efficienza applicando una singola trasformazione composta a un punto, piuttosto che applicare una serie di trasformazioni, una dopo l'altra.
Ad esempio, per ruotare un oggetto su un punto arbitrario (X p , Y p ), dobbiamo eseguire tre passaggi:
- Trasla il punto (X p , Y p ) all'origine.
- Ruotalo intorno all'origine.
- Infine, riporta il centro di rotazione al punto in cui apparteneva.
Nel sistema 2D, usiamo solo due coordinate X e Y ma in 3D viene aggiunta una coordinata Z extra. Le tecniche di grafica 3D e la loro applicazione sono fondamentali per i settori dell'intrattenimento, dei giochi e della progettazione assistita da computer. È un'area di ricerca continua nella visualizzazione scientifica.
Inoltre, i componenti grafici 3D fanno ormai parte di quasi tutti i personal computer e, sebbene tradizionalmente destinati a software ad alta intensità di grafica come i giochi, vengono sempre più utilizzati da altre applicazioni.
Proiezione parallela
La proiezione parallela scarta la coordinata Z e le linee parallele da ogni vertice dell'oggetto vengono estese fino a quando non intersecano il piano della vista. Nella proiezione parallela, specifichiamo una direzione di proiezione invece del centro di proiezione.
Nella proiezione parallela, la distanza dal centro di proiezione al piano di proiezione è infinita. In questo tipo di proiezione, colleghiamo i vertici proiettati mediante segmenti di linea che corrispondono alle connessioni sull'oggetto originale.
Le proiezioni parallele sono meno realistiche, ma vanno bene per misurazioni esatte. In questo tipo di proiezioni, le linee parallele rimangono parallele e gli angoli non vengono preservati. Vari tipi di proiezioni parallele sono mostrati nella seguente gerarchia.
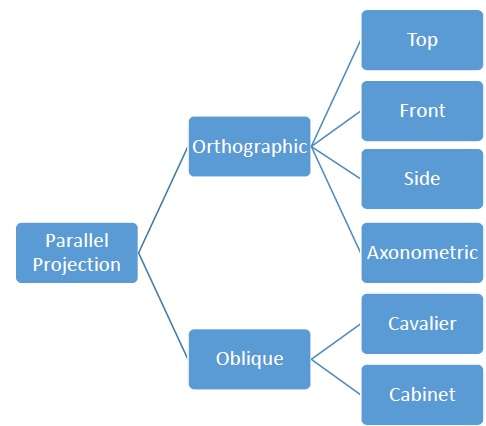
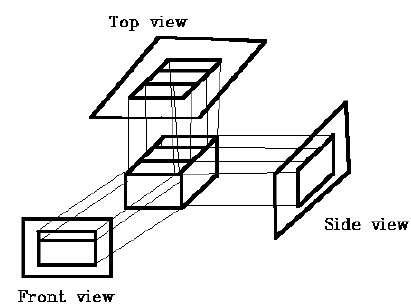
Proiezione ortogonale
Nella proiezione ortografica la direzione della proiezione è normale alla proiezione del piano. Esistono tre tipi di proiezioni ortografiche:
- Proiezione frontale
- Proiezione superiore
- Proiezione laterale
Proiezione obliqua
Nella proiezione obliqua, la direzione della proiezione non è normale alla proiezione dell'aereo. Nella proiezione obliqua, possiamo visualizzare l'oggetto meglio della proiezione ortografica.
Esistono due tipi di proiezioni oblique: Cavalier e Cabinet. La proiezione Cavalier fa un angolo di 45 ° con il piano di proiezione. La proiezione di una linea perpendicolare al piano della vista ha la stessa lunghezza della linea stessa nella proiezione di Cavalier. In una proiezione cavaliere, i fattori di scorcio per tutte e tre le direzioni principali sono uguali.
La proiezione del Cabinet fa un angolo di 63,4 ° con il piano di proiezione. Nella proiezione Cabinet, le linee perpendicolari alla superficie di visualizzazione vengono proiettate a ½ della loro lunghezza effettiva. Entrambe le proiezioni sono mostrate nella figura seguente:

Proiezioni isometriche
Vengono chiamate proiezioni ortografiche che mostrano più di un lato di un oggetto axonometric orthographic projections. La proiezione assonometrica più comune è unaisometric projectiondove il piano di proiezione interseca ogni asse di coordinate nel sistema di coordinate del modello a una distanza uguale. In questa proiezione il parallelismo delle linee viene preservato ma gli angoli non vengono preservati. La figura seguente mostra la proiezione isometrica:

Proiezione prospettica
Nella proiezione prospettica, la distanza dal centro di proiezione al piano di proiezione è finita e la dimensione dell'oggetto varia inversamente con la distanza che sembra più realistica.
La distanza e gli angoli non vengono preservati e le linee parallele non rimangono parallele. Invece, convergono tutti in un unico punto chiamatocenter of projection o projection reference point. Ci sono 3 tipi di proiezioni prospettiche che sono mostrate nella seguente tabella.
One point la proiezione prospettica è semplice da disegnare.
Two point la proiezione prospettica dà una migliore impressione di profondità.
Three point la proiezione prospettica è molto difficile da disegnare.
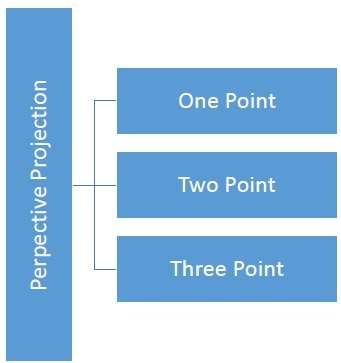
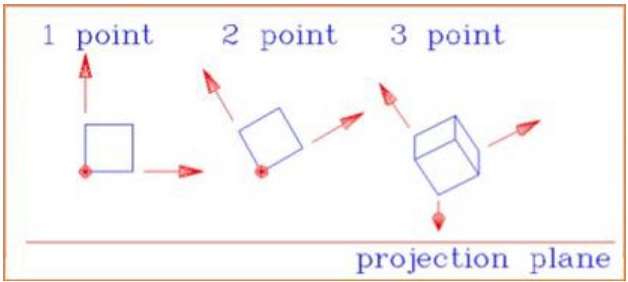
La figura seguente mostra tutti e tre i tipi di proiezione prospettica:
Traduzione
Nella traduzione 3D, trasferiamo la coordinata Z insieme alle coordinate X e Y. Il processo per la traduzione in 3D è simile alla traduzione 2D. Una traduzione sposta un oggetto in una posizione diversa sullo schermo.
La figura seguente mostra l'effetto della traduzione:
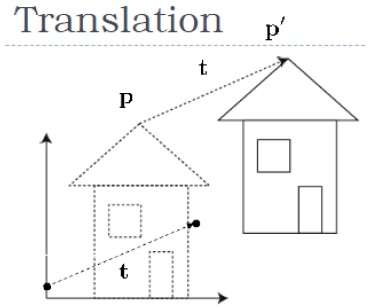
Un punto può essere tradotto in 3D aggiungendo coordinate di traslazione $(t_{x,} t_{y,} t_{z})$ alla coordinata originale (X, Y, Z) per ottenere la nuova coordinata (X ', Y', Z ').
$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$
P '= P ∙ T
$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$
$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$
Rotazione
La rotazione 3D non è la stessa della rotazione 2D. Nella rotazione 3D, dobbiamo specificare l'angolo di rotazione insieme all'asse di rotazione. Possiamo eseguire la rotazione 3D sugli assi X, Y e Z. Sono rappresentati nella forma a matrice come di seguito:
$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$
La figura seguente spiega la rotazione sui vari assi:
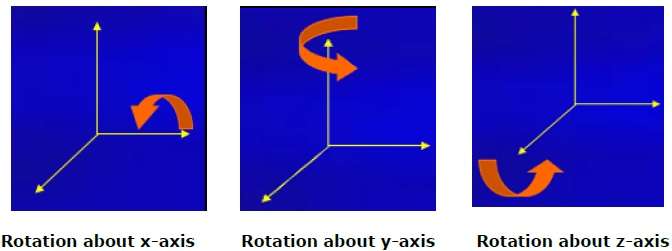
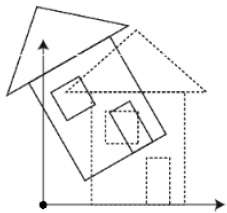
Ridimensionamento
È possibile modificare le dimensioni di un oggetto utilizzando la trasformazione in scala. Nel processo di ridimensionamento, espandi o comprimi le dimensioni dell'oggetto. Il ridimensionamento può essere ottenuto moltiplicando le coordinate originali dell'oggetto per il fattore di scala per ottenere il risultato desiderato. La figura seguente mostra l'effetto del ridimensionamento 3D:
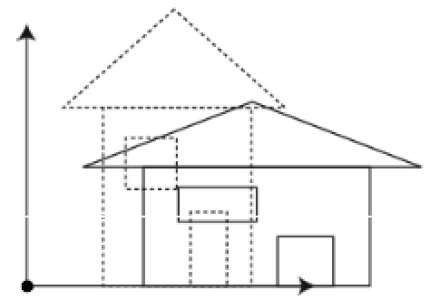
Nell'operazione di ridimensionamento 3D, vengono utilizzate tre coordinate. Supponiamo che le coordinate originali siano (X, Y, Z), i fattori di scala lo sono$(S_{X,} S_{Y,} S_{z})$rispettivamente, e le coordinate prodotte sono (X ', Y', Z '). Questo può essere rappresentato matematicamente come mostrato di seguito:
$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$
P '= P ∙ S
$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$
$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$
Shear
Una trasformazione che inclina la forma di un oggetto è chiamata shear transformation. Come nel taglio 2D, possiamo inclinare un oggetto lungo l'asse X, l'asse Y o l'asse Z in 3D.
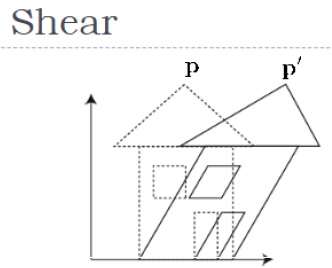
Come mostrato nella figura sopra, c'è una coordinata P. Puoi tranciarla per ottenere una nuova coordinata P ', che può essere rappresentata in forma di matrice 3D come di seguito -
$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$
P '= P ∙ Sh
$X’ = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$
$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$
$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$
Matrici di trasformazione
La matrice di trasformazione è uno strumento di base per la trasformazione. Una matrice con dimensioni nxm viene moltiplicata per la coordinata degli oggetti. Di solito per la trasformazione vengono utilizzate matrici 3 x 3 o 4 x 4. Ad esempio, considera la seguente matrice per varie operazioni.
| $T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$ | $S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$ | $Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$ |
| Translation Matrix | Scaling Matrix | Shear Matrix |
| $R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$ | $R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$ | $R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$ |
| Rotation Matrix | ||
Nella computer grafica, spesso abbiamo bisogno di disegnare diversi tipi di oggetti sullo schermo. Gli oggetti non sono sempre piatti e abbiamo bisogno di disegnare curve molte volte per disegnare un oggetto.
Tipi di curve
Una curva è un insieme infinitamente grande di punti. Ogni punto ha due vicini eccetto gli endpoint. Le curve possono essere classificate in tre categorie:explicit, implicit, e parametric curves.
Curve implicite
Le rappresentazioni implicite della curva definiscono l'insieme di punti su una curva impiegando una procedura che può verificare se un punto si trova sulla curva. Di solito, una curva implicita è definita da una funzione implicita della forma -
f (x, y) = 0
Può rappresentare curve multivalore (più valori y per un valore x). Un esempio comune è il cerchio, la cui rappresentazione implicita è
x2 + y2 - R2 = 0
Curve esplicite
Una funzione matematica y = f (x) può essere tracciata come una curva. Tale funzione è la rappresentazione esplicita della curva. La rappresentazione esplicita non è generale, poiché non può rappresentare linee verticali ed è anche monivalore. Per ogni valore di x, solo un singolo valore di y viene normalmente calcolato dalla funzione.
Curve parametriche
Le curve di forma parametrica sono chiamate curve parametriche. Le rappresentazioni della curva esplicita e implicita possono essere utilizzate solo quando la funzione è nota. In pratica vengono utilizzate le curve parametriche. Una curva parametrica bidimensionale ha la seguente forma:
P (t) = f (t), g (t) o P (t) = x (t), y (t)
Le funzioni feg diventano le coordinate (x, y) di qualsiasi punto della curva, ei punti si ottengono quando il parametro t viene variato su un certo intervallo [a, b], normalmente [0, 1].
Curve di Bézier
La curva di Bézier viene scoperta dall'ingegnere francese Pierre Bézier. Queste curve possono essere generate sotto il controllo di altri punti. Le tangenti approssimative utilizzando i punti di controllo vengono utilizzate per generare la curva. La curva di Bézier può essere rappresentata matematicamente come:
$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$
Dove $p_{i}$ è l'insieme di punti e ${B_{i}^{n}}(t)$ rappresenta i polinomi di Bernstein che sono dati da -
$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i}$$
Dove n è il grado polinomiale, i è l'indice e t è la variabile.
La curva di Bézier più semplice è la linea retta dal punto $P_{0}$ per $P_{1}$. Una curva di Bézier quadratica è determinata da tre punti di controllo. Una curva di Bézier cubica è determinata da quattro punti di controllo.
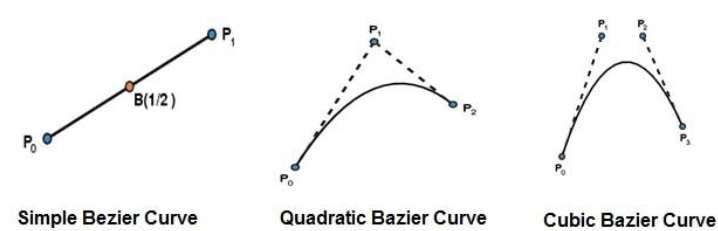
Proprietà delle curve di Bézier
Le curve di Bézier hanno le seguenti proprietà:
Generalmente seguono la forma del poligono di controllo, che consiste dei segmenti che uniscono i punti di controllo.
Passano sempre attraverso il primo e l'ultimo punto di controllo.
Sono contenuti nello scafo convesso dei loro punti di controllo che definiscono.
Il grado del polinomio che definisce il segmento della curva è uno in meno del numero del punto del poligono che definisce. Pertanto, per 4 punti di controllo, il grado del polinomio è 3, cioè polinomio cubico.
Una curva di Bézier generalmente segue la forma del poligono di definizione.
La direzione del vettore tangente nei punti finali è uguale a quella del vettore determinata dal primo e dall'ultimo segmento.
La proprietà convessa dello scafo per una curva di Bézier garantisce che il polinomio segua uniformemente i punti di controllo.
Nessuna linea retta interseca una curva di Bézier più volte di quanto interseca il suo poligono di controllo.
Sono invarianti sotto una trasformazione affine.
Le curve di Bézier mostrano un controllo globale: lo spostamento di un punto di controllo altera la forma dell'intera curva.
Una data curva di Bézier può essere suddivisa in un punto t = t0 in due segmenti di Bézier che si uniscono nel punto corrispondente al valore del parametro t = t0.
Curve B-Spline
La curva di Bezier prodotta dalla funzione di base di Bernstein ha una flessibilità limitata.
Innanzitutto, il numero di vertici poligonali specificati fissa l'ordine del polinomio risultante che definisce la curva.
La seconda caratteristica limitante è che il valore della funzione di fusione è diverso da zero per tutti i valori dei parametri sull'intera curva.
La base B-spline contiene la base Bernstein come caso speciale. La base B-spline non è globale.
Una curva B-spline è definita come una combinazione lineare di punti di controllo Pi e funzione base B-spline $N_{i,}$ k (t) dato da
$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$
Dove,
{$p_{i}$: i = 0, 1, 2… .n} sono i punti di controllo
k è l'ordine dei segmenti polinomiali della curva B-spline. Ordine k significa che la curva è composta da segmenti polinomiali a tratti di grado k - 1,
il $N_{i,k}(t)$sono le "funzioni di fusione B-spline normalizzate". Sono descritti dall'ordine k e da una sequenza non decrescente di numeri reali normalmente chiamata “sequenza di nodi”.
$${t_{i}:i = 0, ... n + K}$$
Le funzioni N i , k sono descritte come segue:
$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& Otherwise \end{matrix}\right.$$
e se k> 1,
$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$
e
$$t \: \epsilon \: [t_{k-1},t_{n+1})$$
Proprietà della curva B-spline
Le curve B-spline hanno le seguenti proprietà:
La somma delle funzioni base B-spline per qualsiasi valore di parametro è 1.
Ogni funzione di base è positiva o zero per tutti i valori dei parametri.
Ogni funzione di base ha esattamente un valore massimo, ad eccezione di k = 1.
L'ordine massimo della curva è uguale al numero di vertici di definizione del poligono.
Il grado del polinomio B-spline è indipendente dal numero di vertici del poligono di definizione.
B-spline consente il controllo locale sulla superficie della curva poiché ogni vertice influisce sulla forma di una curva solo su un intervallo di valori dei parametri in cui la funzione di base associata è diversa da zero.
La curva mostra la proprietà di diminuzione della variazione.
La curva generalmente segue la forma del poligono di definizione.
Qualsiasi trasformazione affine può essere applicata alla curva applicandola ai vertici del poligono di definizione.
La linea curva all'interno dello scafo convesso del poligono che lo definisce.
Superfici poligonali
Gli oggetti sono rappresentati come una raccolta di superfici. La rappresentazione degli oggetti 3D è divisa in due categorie.
Boundary Representations (B-reps) - Descrive un oggetto 3D come un insieme di superfici che separa l'interno dell'oggetto dall'ambiente.
Space–partitioning representations - Viene utilizzato per descrivere le proprietà interne, partizionando la regione spaziale contenente un oggetto in un insieme di solidi piccoli, non sovrapposti e contigui (solitamente cubi).
La rappresentazione del contorno più comunemente usata per un oggetto grafico 3D è un insieme di poligoni di superficie che racchiudono l'interno dell'oggetto. Molti sistemi grafici utilizzano questo metodo. Set di poligoni vengono memorizzati per la descrizione dell'oggetto. Ciò semplifica e accelera il rendering della superficie e la visualizzazione dell'oggetto poiché tutte le superfici possono essere descritte con equazioni lineari.
Le superfici poligonali sono comuni nelle applicazioni di progettazione e modellazione solida, dal momento che la loro wireframe displaypuò essere eseguito rapidamente per fornire un'indicazione generale della struttura della superficie. Quindi vengono prodotte scene realistiche interpolando motivi di ombreggiatura sulla superficie del poligono per illuminarli.
Tabelle poligonali
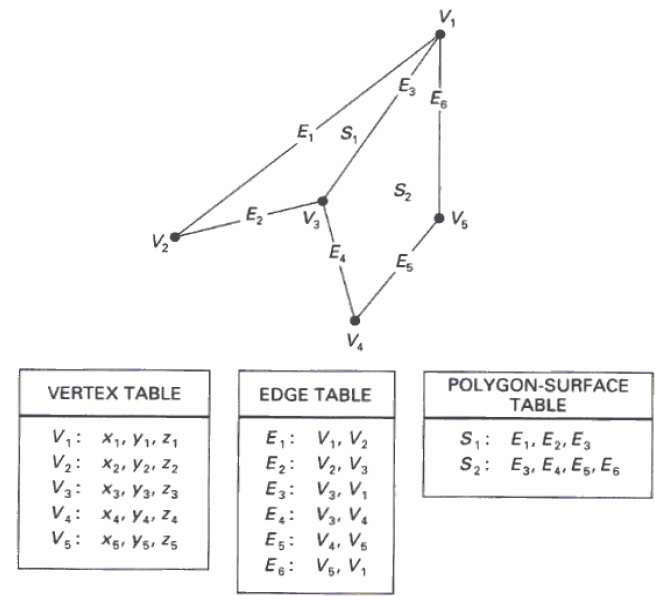
In questo metodo, la superficie è specificata dall'insieme di coordinate del vertice e attributi associati. Come mostrato nella figura seguente, ci sono cinque vertici, da v 1 a v 5 .
Ogni vertice memorizza le informazioni sulle coordinate x, yez rappresentate nella tabella come v 1 : x 1 , y 1 , z 1 .
La tabella Edge viene utilizzata per memorizzare le informazioni sul bordo del poligono. Nella figura seguente, il bordo E 1 si trova tra i vertici v 1 e v 2 che è rappresentato nella tabella come E 1 : v 1 , v 2 .
La tabella delle superfici poligonali memorizza il numero di superfici presenti nel poligono. Dalla figura seguente, la superficie S 1 è coperta dai bordi E 1 , E 2 ed E 3 che possono essere rappresentati nella tabella della superficie poligonale come S 1 : E 1 , E 2 ed E 3 .
Equazioni piane
L'equazione per la superficie piana può essere espressa come -
Ax + By + Cz + D = 0
Dove (x, y, z) è un punto qualsiasi del piano ei coefficienti A, B, C e D sono costanti che descrivono le proprietà spaziali del piano. Possiamo ottenere i valori di A, B, C e D risolvendo un insieme di tre equazioni piane utilizzando i valori delle coordinate per tre punti non collineari nel piano. Supponiamo che tre vertici del piano siano (x 1 , y 1 , z 1 ), (x 2 , y 2 , z 2 ) e (x 3 , y 3 , z 3 ).
Risolviamo le seguenti equazioni simultanee per i rapporti A / D, B / D e C / D. Ottieni i valori di A, B, C e D.
(A / D) x 1 + (B / D) y 1 + (C / D) z 1 = -1
(A / D) x 2 + (B / D) y 2 + (C / D) z 2 = -1
(A / D) x 3 + (B / D) y 3 + (C / D) z 3 = -1
Per ottenere le equazioni di cui sopra in forma determinante, applica la regola di Cramer alle equazioni di cui sopra.
$A = \begin{bmatrix} 1& y_{1}& z_{1}\\ 1& y_{2}& z_{2}\\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\\ x_{2}& 1& z_{2}\\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\\ x_{2}& y_{2}& 1\\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\\ x_{2}& y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$
Per qualsiasi punto (x, y, z) con parametri A, B, C e D, possiamo dire che -
Ax + By + Cz + D ≠ 0 significa che il punto non è sul piano.
Ax + By + Cz + D <0 significa che il punto è all'interno della superficie.
Ax + By + Cz + D> 0 significa che il punto è al di fuori della superficie.
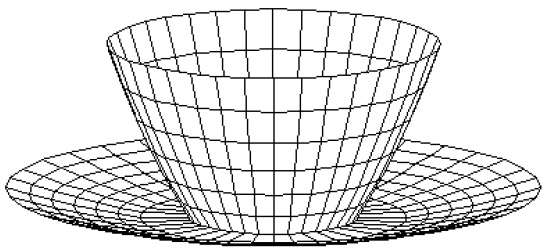
Mesh poligonali
Le superfici 3D e i solidi possono essere approssimati da un insieme di elementi poligonali e lineari. Tali superfici sono chiamatepolygonal meshes. Nella mesh poligonale, ogni bordo è condiviso da un massimo di due poligoni. L'insieme di poligoni o facce, insieme formano la "pelle" dell'oggetto.
Questo metodo può essere utilizzato per rappresentare un'ampia classe di solidi / superfici nella grafica. Una mesh poligonale può essere renderizzata utilizzando algoritmi di rimozione della superficie nascosta. La mesh poligonale può essere rappresentata in tre modi:
- Rappresentazione esplicita
- Puntatori a un elenco di vertici
- Puntatori a un elenco di bordi
Vantaggi
- Può essere utilizzato per modellare quasi tutti gli oggetti.
- Sono facili da rappresentare come una raccolta di vertici.
- Sono facili da trasformare.
- Sono facili da disegnare sullo schermo del computer.
Svantaggi
- Le superfici curve possono essere descritte solo approssimativamente.
- È difficile simulare alcuni tipi di oggetti come capelli o liquidi.
Quando guardiamo un'immagine contenente oggetti e superfici non trasparenti, non possiamo vedere quegli oggetti che si trovano dietro agli oggetti più vicini all'occhio. Dobbiamo rimuovere queste superfici nascoste per ottenere un'immagine realistica dello schermo. Viene chiamata l'identificazione e la rimozione di queste superficiHidden-surface problem.
Esistono due approcci per rimuovere i problemi di superficie nascosta: Object-Space method e Image-space method. Il metodo Object-space è implementato nel sistema di coordinate fisico e il metodo image-space è implementato nel sistema di coordinate dello schermo.
Quando vogliamo visualizzare un oggetto 3D su uno schermo 2D, dobbiamo identificare quelle parti di uno schermo che sono visibili da una posizione di visualizzazione scelta.
Metodo Depth Buffer (Z-Buffer)
Questo metodo è sviluppato da Cutmull. È un approccio spazio-immagine. L'idea di base è testare la profondità Z di ciascuna superficie per determinare la superficie (visibile) più vicina.
In questo metodo ogni superficie viene elaborata separatamente, una posizione pixel alla volta sulla superficie. I valori di profondità di un pixel vengono confrontati e la superficie più vicina (z più piccola) determina il colore da visualizzare nel frame buffer.
Si applica in modo molto efficiente sulle superfici del poligono. Le superfici possono essere lavorate in qualsiasi ordine. Per sovrascrivere i poligoni più vicini da quelli più lontani, due buffer denominatiframe buffer e depth buffer, sono usati.
Depth buffer viene utilizzato per memorizzare i valori di profondità per la posizione (x, y), mentre le superfici vengono elaborate (0 ≤ profondità ≤ 1).
Il frame buffer viene utilizzato per memorizzare il valore di intensità del valore del colore in ciascuna posizione (x, y).
Le coordinate z sono normalmente normalizzate nell'intervallo [0, 1]. Il valore 0 per la coordinata z indica il riquadro di ritaglio posteriore e il valore 1 per le coordinate z indica il riquadro di ritaglio anteriore.
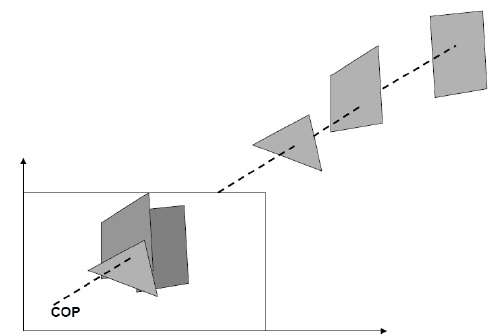
Algoritmo
Step-1 - Impostare i valori del tampone -
Buffer di profondità (x, y) = 0
Framebuffer (x, y) = colore di sfondo
Step-2 - Elabora ogni poligono (uno alla volta)
Per ogni posizione di pixel proiettata (x, y) di un poligono, calcolare la profondità z.
Se Z> buffer di profondità (x, y)
Calcola il colore della superficie,
imposta il buffer di profondità (x, y) = z,
framebuffer (x, y) = colore della superficie (x, y)
Vantaggi
- È facile da implementare.
- Riduce il problema di velocità se implementato nell'hardware.
- Elabora un oggetto alla volta.
Svantaggi
- Richiede una grande memoria.
- È un processo che richiede tempo.
Metodo linea di scansione
È un metodo dello spazio dell'immagine per identificare la superficie visibile. Questo metodo ha informazioni sulla profondità solo per una singola linea di scansione. Per richiedere una linea di scansione di valori di profondità, dobbiamo raggruppare ed elaborare tutti i poligoni che intersecano una data linea di scansione contemporaneamente prima di elaborare la successiva linea di scansione. Due tabelle importanti,edge table e polygon table, vengono mantenuti per questo.
The Edge Table - Contiene i punti finali delle coordinate di ciascuna linea nella scena, la pendenza inversa di ciascuna linea e i puntatori nella tabella dei poligoni per collegare i bordi alle superfici.
The Polygon Table - Contiene i coefficienti del piano, le proprietà del materiale della superficie, altri dati sulla superficie e può essere un puntatore alla tabella dei bordi.

Per facilitare la ricerca di superfici che attraversano una data linea di scansione, viene formato un elenco attivo di bordi. L'elenco attivo memorizza solo quei bordi che attraversano la linea di scansione in ordine crescente di x. Inoltre, una bandiera è impostata per ogni superficie per indicare se una posizione lungo una linea di scansione è all'interno o all'esterno della superficie.
Le posizioni dei pixel su ciascuna linea di scansione vengono elaborate da sinistra a destra. All'intersezione a sinistra con una superficie, la bandiera di superficie è attivata ea destra, la bandiera è disattivata. È necessario eseguire calcoli di profondità solo quando più superfici hanno i flag attivati in una determinata posizione della linea di scansione.
Metodo di suddivisione dell'area
Il metodo di suddivisione dell'area sfrutta l'individuazione di quelle aree di visualizzazione che rappresentano parte di una singola superficie. Dividere l'area di visualizzazione totale in rettangoli sempre più piccoli fino a quando ogni piccola area è la proiezione di una parte di una singola superficie visibile o nessuna superficie.
Continuare questo processo fino a quando le suddivisioni non vengono facilmente analizzate come appartenenti a una singola superficie o fino a quando non vengono ridotte alle dimensioni di un singolo pixel. Un modo semplice per farlo è dividere successivamente l'area in quattro parti uguali ad ogni passaggio. Esistono quattro possibili relazioni che una superficie può avere con un contorno di area specificato.
Surrounding surface - Uno che racchiuda completamente l'area.
Overlapping surface - Uno che è in parte all'interno e in parte all'esterno dell'area.
Inside surface - Uno che sia completamente all'interno dell'area.
Outside surface - Uno che è completamente al di fuori dell'area.
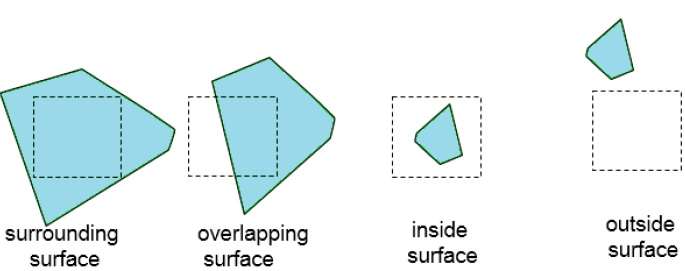
I test per determinare la visibilità della superficie all'interno di un'area possono essere stabiliti in base a queste quattro classificazioni. Non sono necessarie ulteriori suddivisioni di un'area specifica se si verifica una delle seguenti condizioni:
- Tutte le superfici sono superfici esterne rispetto all'area.
- Solo una superficie interna, sovrapposta o circostante si trova nell'area.
- Una superficie circostante oscura tutte le altre superfici all'interno dei confini dell'area.
Rilevamento faccia posteriore
Un metodo veloce e semplice dello spazio oggetto per identificare le facce posteriori di un poliedro si basa sui test "interno-esterno". Un punto (x, y, z) è "all'interno" di una superficie poligonale con parametri di piano A, B, C e D se Quando un punto interno si trova lungo la linea di vista verso la superficie, il poligono deve essere una faccia posteriore ( siamo all'interno di quella faccia e non possiamo vederne la parte anteriore dalla nostra posizione di visione).
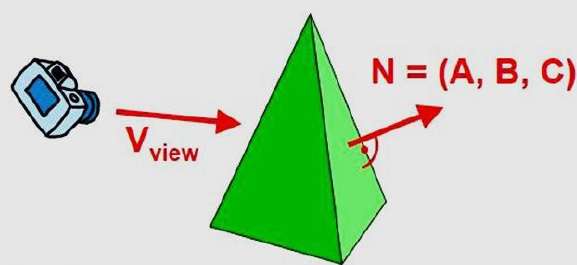
Possiamo semplificare questo test considerando il vettore normale N a una superficie poligonale, che ha componenti cartesiane (A, B, C).
In generale, se V è un vettore nella direzione di visione dalla posizione dell'occhio (o della "telecamera"), questo poligono è una faccia posteriore se
V.N > 0
Inoltre, se le descrizioni degli oggetti vengono convertite in coordinate di proiezione e la direzione di visualizzazione è parallela all'asse z di visualizzazione, allora:
V = (0, 0, V z ) e V.N = V Z C
Quindi dobbiamo solo considerare il segno di C la componente del vettore normale N.
In un sistema di visione destrorso con direzione di visione lungo il negativo $Z_{V}$asse, il poligono è una faccia posteriore se C <0. Inoltre, non possiamo vedere alcuna faccia la cui normale ha componente z C = 0, poiché la direzione di visualizzazione è verso quel poligono. Quindi, in generale, possiamo etichettare qualsiasi poligono come faccia posteriore se il suo vettore normale ha il valore del componente az -
C <= 0
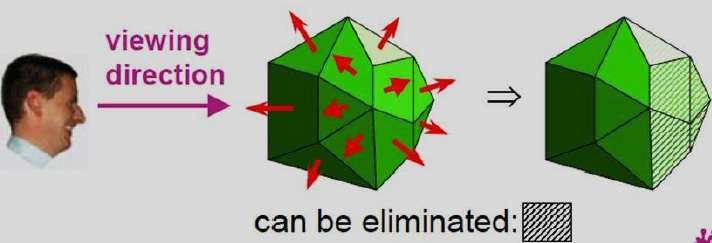
Metodi simili possono essere utilizzati in pacchetti che utilizzano un sistema di visualizzazione per mancini. In questi pacchetti, i parametri del piano A, B, C e D possono essere calcolati dalle coordinate del vertice del poligono specificate in senso orario (a differenza della direzione antioraria usata in un sistema destrorso).
Inoltre, le facce posteriori hanno vettori normali che puntano lontano dalla posizione di visualizzazione e sono identificate da C> = 0 quando la direzione di visualizzazione è lungo il positivo $Z_{v}$asse. Esaminando il parametro C per i diversi piani che definiscono un oggetto, possiamo immediatamente identificare tutte le facce posteriori.
Metodo A-Buffer
Il metodo A-buffer è un'estensione del metodo depth-buffer. Il metodo A-buffer è un metodo di rilevamento della visibilità sviluppato presso Lucas Film Studios per il sistema di rendering Renders Everything You Ever Saw (REYES).
Il buffer A espande il metodo del buffer di profondità per consentire le trasparenze. La struttura dei dati chiave nell'A-buffer è il buffer di accumulo.
Ogni posizione nell'A-buffer ha due campi:
Depth field - Memorizza un numero reale positivo o negativo
Intensity field - Memorizza le informazioni sull'intensità della superficie o un valore del puntatore

Se depth> = 0, il numero memorizzato in quella posizione è la profondità di una singola superficie che si sovrappone all'area pixel corrispondente. Il campo di intensità memorizza quindi i componenti RGB del colore della superficie in quel punto e la percentuale di copertura dei pixel.
Se la profondità è <0, indica contributi su più superfici all'intensità dei pixel. Il campo di intensità memorizza quindi un puntatore a un elenco collegato di dati di superficie. Il buffer di superficie nell'A-buffer include:
- Componenti dell'intensità RGB
- Parametro di opacità
- Depth
- Percentuale di copertura dell'area
- Identificatore di superficie
L'algoritmo procede proprio come l'algoritmo del buffer di profondità. I valori di profondità e opacità vengono utilizzati per determinare il colore finale di un pixel.
Metodo di ordinamento della profondità
Il metodo di ordinamento in profondità utilizza sia lo spazio immagine che le operazioni spazio oggetti. Il metodo di ordinamento in profondità esegue due funzioni di base:
Innanzitutto, le superfici vengono ordinate in ordine di profondità decrescente.
In secondo luogo, le superfici vengono convertite in scansione in ordine, a partire dalla superficie di maggiore profondità.
La conversione della scansione delle superfici poligonali viene eseguita nello spazio dell'immagine. Questo metodo per risolvere il problema della superficie nascosta è spesso indicato comepainter's algorithm. La figura seguente mostra l'effetto dell'ordinamento di profondità:
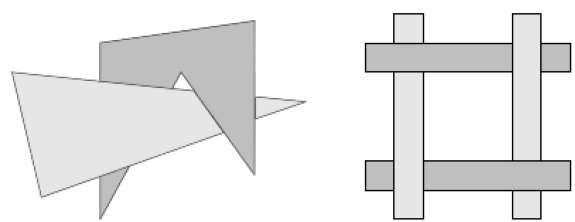
L'algoritmo inizia con l'ordinamento in base alla profondità. Ad esempio, la stima iniziale della "profondità" di un poligono può essere considerata il valore z più vicino a qualsiasi vertice del poligono.
Prendiamo il poligono P alla fine della lista. Considera tutti i poligoni Q le cui estensioni z si sovrappongono a quelle di P. Prima di disegnare P, eseguiamo i seguenti test. Se uno qualsiasi dei seguenti test è positivo, possiamo supporre che P possa essere disegnato prima di Q.
- Le estensioni x non si sovrappongono?
- Le estensioni y non si sovrappongono?
- P è interamente sul lato opposto del piano di Q dal punto di vista?
- Q è interamente sullo stesso lato del piano di P del punto di vista?
- Le proiezioni dei poligoni non si sovrappongono?
Se tutti i test falliscono, allora dividiamo P o Q usando il piano dell'altro. I nuovi poligoni tagliati vengono inseriti nell'ordine di profondità e il processo continua. Teoricamente, questo partizionamento potrebbe generare O (n 2 ) poligoni individuali, ma in pratica il numero di poligoni è molto inferiore.
Alberi di partizione spaziale binaria (BSP)
Il partizionamento binario dello spazio viene utilizzato per calcolare la visibilità. Per costruire gli alberi BSP, si dovrebbe iniziare con i poligoni ed etichettare tutti i bordi. Avendo a che fare con un solo bordo alla volta, estendi ciascun bordo in modo che divida il piano in due. Posiziona il primo bordo dell'albero come radice. Aggiungi i bordi successivi in base al fatto che siano interni o esterni. I bordi che si estendono sull'estensione di un bordo già presente nell'albero vengono divisi in due ed entrambi vengono aggiunti all'albero.

Dalla figura sopra, prima prendere A come radice.
Fai un elenco di tutti i nodi nella figura (a).
Metti tutti i nodi che si trovano davanti a root A sul lato sinistro del nodo A e metti tutti quei nodi che stanno dietro la radice A a destra come mostrato in figura (b).
Elaborare prima tutti i nodi anteriori e poi i nodi posteriori.
Come mostrato nella figura (c), elaboreremo prima il nodo B. Poiché non c'è nulla davanti al nodoB, abbiamo messo NIL. Tuttavia, abbiamo nodeC sul retro del nodo B, quindi nodo C andrà sul lato destro del nodo B.
Ripeti la stessa procedura per il nodo D.
Un matematico franco-americano, il dottor Benoit Mandelbrot, ha scoperto i frattali. La parola frattale deriva da una parola latina fractus che significa rotto.
Cosa sono i frattali?
I frattali sono immagini molto complesse generate da un computer da un'unica formula. Vengono creati utilizzando iterazioni. Ciò significa che una formula viene ripetuta con valori leggermente diversi più e più volte, tenendo conto dei risultati dell'iterazione precedente.
I frattali sono usati in molte aree come:
Astronomy - Per analizzare galassie, anelli di Saturno, ecc.
Biology/Chemistry - Per rappresentare colture batteriche, reazioni chimiche, anatomia umana, molecole, piante,
Others - Per rappresentare nuvole, coste e confini, compressione dei dati, diffusione, economia, arte frattale, musica frattale, paesaggi, effetti speciali, ecc.

Generazione di frattali
I frattali possono essere generati ripetendo la stessa forma più e più volte come mostrato nella figura seguente. Nella figura (a) mostra un triangolo equilatero. Nella figura (b), possiamo vedere che il triangolo viene ripetuto per creare una forma a stella. Nella figura (c), possiamo vedere che la forma a stella nella figura (b) viene ripetuta ancora e ancora per creare una nuova forma.
Possiamo fare un numero illimitato di iterazioni per creare una forma desiderata. In termini di programmazione, la ricorsione viene utilizzata per creare tali forme.

Frattali geometrici
I frattali geometrici si occupano di forme trovate in natura che hanno dimensioni non intere o frattali. Per costruire geometricamente un frattale auto-simile deterministico (non casuale), iniziamo con una data forma geometrica, chiamatainitiator. Le sottoparti dell'iniziatore vengono quindi sostituite con un modello, chiamatogenerator.

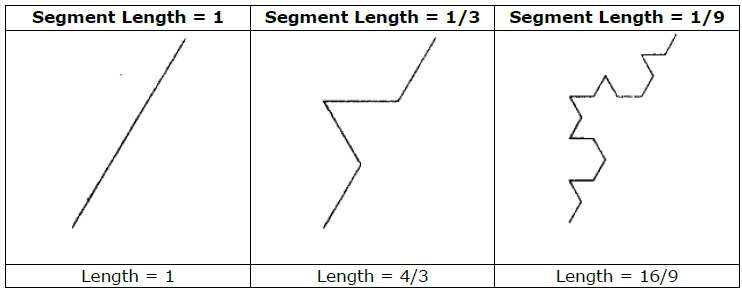
Ad esempio, se usiamo l'iniziatore e il generatore mostrati nella figura sopra, possiamo costruire un buon pattern ripetendolo. Ogni segmento di linea retta nell'iniziatore viene sostituito con quattro segmenti di linea di uguale lunghezza ad ogni passaggio. Il fattore di scala è 1/3, quindi la dimensione frattale è D = ln 4 / ln 3 ≈ 1,2619.
Inoltre, la lunghezza di ogni segmento di linea nell'iniziatore aumenta di un fattore 4/3 ad ogni passo, in modo che la lunghezza della curva frattale tenda all'infinito quando vengono aggiunti più dettagli alla curva come mostrato nella figura seguente -
Animare significa dare vita a qualsiasi oggetto in computer grafica. Ha il potere di iniettare energia ed emozioni negli oggetti apparentemente inanimati. L'animazione computerizzata e l'animazione generata dal computer sono due categorie di animazione al computer. Può essere presentato tramite film o video.
L'idea di base dietro l'animazione è riprodurre le immagini registrate a velocità sufficientemente veloci da indurre l'occhio umano a interpretarle come movimento continuo. L'animazione può dare vita a una serie di immagini morte. L'animazione può essere utilizzata in molte aree come l'intrattenimento, la progettazione assistita da computer, la visualizzazione scientifica, la formazione, l'istruzione, l'e-commerce e la computer art.
Tecniche di animazione
Gli animatori hanno inventato e utilizzato una varietà di diverse tecniche di animazione. Fondamentalmente ci sono sei tecniche di animazione che discuteremo una per una in questa sezione.
Animazione tradizionale (fotogramma per fotogramma)
Tradizionalmente la maggior parte dell'animazione veniva eseguita a mano. Tutti i fotogrammi di un'animazione dovevano essere disegnati a mano. Poiché ogni secondo di animazione richiede 24 fotogrammi (film), la quantità di sforzi necessari per creare anche il più breve dei filmati può essere enorme.
Keyframing
In questa tecnica, viene disposto uno storyboard e quindi gli artisti disegnano i principali fotogrammi dell'animazione. I frame principali sono quelli in cui avvengono cambiamenti importanti. Sono i punti chiave dell'animazione. Il keyframing richiede che l'animatore specifichi le posizioni critiche o chiave per gli oggetti. Il computer quindi riempie automaticamente i fotogrammi mancanti interpolando uniformemente tra quelle posizioni.
Procedurale
In un'animazione procedurale, gli oggetti sono animati da una procedura - un insieme di regole - non da keyframing. L'animatore specifica le regole e le condizioni iniziali ed esegue la simulazione. Le regole sono spesso basate su regole fisiche del mondo reale espresse da equazioni matematiche.
comportamentale
Nell'animazione comportamentale, un personaggio autonomo determina le proprie azioni, almeno in una certa misura. Questo dà al personaggio una certa capacità di improvvisare e libera l'animatore dalla necessità di specificare ogni dettaglio del movimento di ogni personaggio.
Basato sulle prestazioni (Motion Capture)
Un'altra tecnica è Motion Capture, in cui sensori magnetici o basati sulla visione registrano le azioni di un oggetto umano o animale in tre dimensioni. Un computer utilizza quindi questi dati per animare l'oggetto.
Questa tecnologia ha consentito a numerosi atleti famosi di fornire le azioni per i personaggi nei videogiochi sportivi. Il motion capture è piuttosto popolare tra gli animatori principalmente perché alcune delle azioni umane comuni possono essere catturate con relativa facilità. Tuttavia, possono esserci gravi discrepanze tra le forme o le dimensioni del soggetto e il carattere grafico e questo può portare a problemi di esatta esecuzione.
Basato fisicamente (dinamica)
A differenza dell'inquadratura chiave e delle immagini in movimento, la simulazione utilizza le leggi della fisica per generare il movimento di immagini e altri oggetti. Le simulazioni possono essere facilmente utilizzate per produrre sequenze leggermente diverse mantenendo il realismo fisico. In secondo luogo, le simulazioni in tempo reale consentono un più alto grado di interattività in cui la persona reale può manovrare le azioni del personaggio simulato.
Al contrario, le applicazioni basate sui fotogrammi chiave e sul movimento selezionano e modificano i movimenti formano una libreria di movimenti precalcolata. Uno degli svantaggi di cui soffre la simulazione è l'esperienza e il tempo necessari per realizzare a mano i sistemi di controllo appropriati.
Framing chiave
Un fotogramma chiave è un fotogramma in cui definiamo i cambiamenti nell'animazione. Ogni fotogramma è un fotogramma chiave quando creiamo un'animazione fotogramma per fotogramma. Quando qualcuno crea un'animazione 3D su un computer, di solito non specifica la posizione esatta di un dato oggetto su ogni singolo fotogramma. Creano fotogrammi chiave.
I fotogrammi chiave sono fotogrammi importanti durante i quali un oggetto cambia le sue dimensioni, direzione, forma o altre proprietà. Il computer quindi calcola tutti i fotogrammi intermedi e risparmia un'estrema quantità di tempo per l'animatore. Le seguenti illustrazioni raffigurano i frame disegnati dall'utente e i frame generati dal computer.


Morphing
La trasformazione delle forme degli oggetti da una forma all'altra è chiamata morphing. È una delle trasformazioni più complicate.

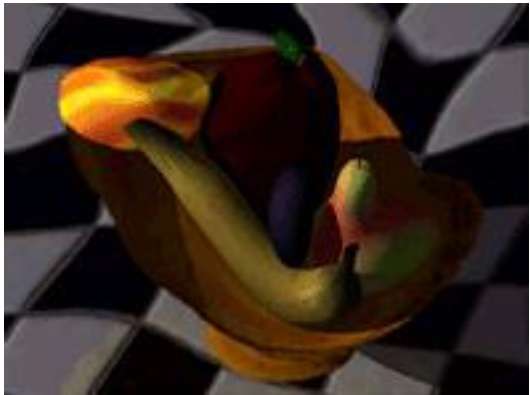
Una metamorfosi sembra come se due immagini si fondessero l'una nell'altra con un movimento molto fluido. In termini tecnici, due immagini sono distorte e si verifica una dissolvenza tra di loro.