Struttura dei dati e algoritmi - Alberi AVL
Cosa succede se l'input dell'albero di ricerca binario arriva in un modo ordinato (crescente o decrescente)? Sarà quindi simile a questo:

Si osserva che la prestazione nel caso peggiore di BST è la più vicina agli algoritmi di ricerca lineare, ovvero Ο (n). Nei dati in tempo reale, non possiamo prevedere il modello dei dati e le loro frequenze. Quindi, sorge la necessità di bilanciare la BST esistente.
Prende il nome dal loro inventore Adelson, Velski & Landis, AVL treessono l'albero di ricerca binario di bilanciamento dell'altezza. L'albero AVL controlla l'altezza dei sottoalberi sinistro e destro e assicura che la differenza non sia maggiore di 1. Questa differenza è chiamataBalance Factor.
Qui vediamo che il primo albero è bilanciato e i due alberi successivi non sono bilanciati -
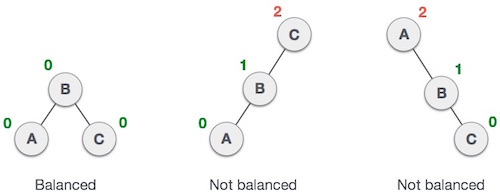
Nel secondo albero, la sottostruttura sinistra di C ha altezza 2 e il sottoalbero destro ha altezza 0, quindi la differenza è 2. Nel terzo albero, il sottoalbero destro di Aha altezza 2 e manca la sinistra, quindi è 0 e la differenza è di nuovo 2. L'albero AVL consente che la differenza (fattore di equilibrio) sia solo 1.
BalanceFactor = height(left-sutree) − height(right-sutree)Se la differenza di altezza tra i sottoalberi sinistro e destro è maggiore di 1, l'albero viene bilanciato utilizzando alcune tecniche di rotazione.
Rotazioni AVL
Per bilanciarsi, un albero AVL può eseguire i seguenti quattro tipi di rotazioni:
- Rotazione a sinistra
- Rotazione a destra
- Rotazione sinistra-destra
- Rotazione destra-sinistra
Le prime due rotazioni sono rotazioni singole e le due rotazioni successive sono rotazioni doppie. Per avere un albero sbilanciato, abbiamo bisogno almeno di un albero di altezza 2. Con questo albero semplice, capiamoli uno per uno.
Rotazione a sinistra
Se un albero diventa sbilanciato, quando un nodo viene inserito nella sottostruttura destra della sottostruttura destra, allora eseguiamo una singola rotazione sinistra -

Nel nostro esempio, node Aè diventato sbilanciato quando un nodo viene inserito nella sottostruttura destra della sottostruttura destra di A. Eseguiamo la rotazione sinistra facendoA la sottostruttura sinistra di B.
Rotazione a destra
L'albero AVL può diventare sbilanciato, se un nodo viene inserito nella sottostruttura sinistra della sottostruttura sinistra. L'albero ha quindi bisogno di una giusta rotazione.

Come illustrato, il nodo sbilanciato diventa il figlio destro del figlio sinistro eseguendo una rotazione a destra.
Rotazione sinistra-destra
Le doppie rotazioni sono versioni leggermente complesse delle versioni già spiegate delle rotazioni. Per capirli meglio, dovremmo prendere nota di ogni azione eseguita durante la rotazione. Controlliamo prima come eseguire la rotazione sinistra-destra. Una rotazione sinistra-destra è una combinazione di rotazione sinistra seguita da rotazione destra.
| Stato | Azione |
|---|---|

|
Un nodo è stato inserito nella sottostruttura destra della sottostruttura sinistra. Questo faCun nodo sbilanciato. Questi scenari fanno sì che l'albero AVL esegua la rotazione da sinistra a destra. |

|
Per prima cosa eseguiamo la rotazione sinistra sulla sottostruttura sinistra di C. Questo faA, la sottostruttura sinistra di B. |

|
Nodo C è ancora sbilanciato, tuttavia ora è a causa della sottostruttura sinistra della sottostruttura sinistra. |

|
Ora ruoteremo a destra l'albero, creando B il nuovo nodo radice di questa sottostruttura. C ora diventa la sottostruttura destra della propria sottostruttura sinistra. |

|
L'albero è ora equilibrato. |
Rotazione destra-sinistra
Il secondo tipo di doppia rotazione è la rotazione destra-sinistra. È una combinazione di rotazione a destra seguita da rotazione a sinistra.
| Stato | Azione |
|---|---|

|
Un nodo è stato inserito nella sottostruttura sinistra della sottostruttura destra. Questo faA, un nodo sbilanciato con fattore di equilibrio 2. |

|
Per prima cosa, eseguiamo la rotazione corretta C nodo, fabbricazione C la sottostruttura destra della propria sottostruttura sinistra B. Adesso,B diventa la sottostruttura destra di A. |

|
Nodo A è ancora sbilanciato a causa del sottoalbero destro del suo sottoalbero destro e richiede una rotazione sinistra. |

|
Una rotazione a sinistra viene eseguita facendo B il nuovo nodo radice della sottostruttura. A diventa la sottostruttura sinistra della relativa sottostruttura destra B. |

|
L'albero è ora equilibrato. |