Teoria dei grafi - Insiemi indipendenti

Gli insiemi indipendenti sono rappresentati in insiemi, in cui

• non dovrebbe esserci any edges adjacent to each other. Non dovrebbe esserci alcun vertice comune tra due spigoli.

• non dovrebbe esserci any vertices adjacent to each other. Non dovrebbe esserci alcun bordo comune tra due vertici.

Set di linee indipendenti

Sia 'G' = (V, E) un grafico. Un sottoinsieme L di E è chiamato insieme di linee indipendenti di 'G' se non ci sono due archi adiacenti in L. Tale insieme è chiamato insieme di linee indipendente.

Example

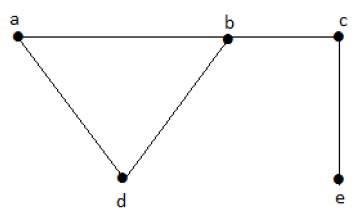
Consideriamo i seguenti sottoinsiemi:

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

In questo esempio, i sottoinsiemi L2 e L3 non sono chiaramente i bordi adiacenti nel grafico dato. Sono insiemi di linee indipendenti. Tuttavia L1 non è un insieme di linee indipendente, poiché per creare un insieme di linee indipendente dovrebbero esserci almeno due bordi.

Set massimo di linee indipendenti

Si dice che un insieme di linee indipendente sia il massimo insieme di linee indipendenti di un grafico "G" se nessun altro arco di "G" può essere aggiunto a "L".

Example

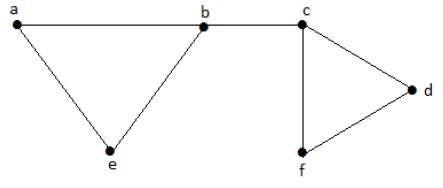
Consideriamo i seguenti sottoinsiemi:

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₂ e L ₃ sono insiemi di linee indipendenti massime / corrispondenza massima. Per quanto riguarda solo questi due sottoinsiemi, non c'è possibilità di aggiungere altri bordi che non siano adiacenti. Quindi questi due sottoinsiemi sono considerati come i massimi insiemi di linee indipendenti.

Numero massimo di linee indipendenti

Un insieme di linee indipendenti massimo di "G" con il numero massimo di bordi è chiamato insieme di linee indipendenti massimo di "G".

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

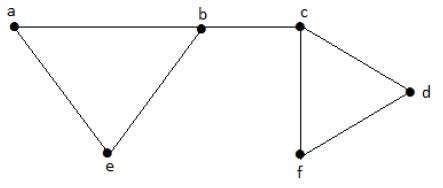
Consideriamo i seguenti sottoinsiemi:

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₃ è il massimo insieme di linee indipendenti di G con i bordi massimi che non sono i bordi adiacenti nel grafico ed è indicato con β1 = 3.

Note - Per qualsiasi grafo G senza vertice isolato,

α1 + β1 = numero di vertici in un grafo = | V |

Example

Numero di copertura linea di K _n / C _n / w _n ,

$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {cases} \ frac {n} {2} \: if \: n \: is \: even \\\ frac {n + 1} {2} \: if \: n \: is \: odd \ end {cases} $$

Numero indipendente dalla riga (numero corrispondente) = β ₁ = [n / 2] α ₁ + β ₁ = n.

Set di vertici indipendenti

Sia 'G' = (V, E) un grafico. Un sottoinsieme di "V" è chiamato un insieme indipendente di "G" se non ci sono due vertici in "S" adiacenti.

Example

Considera i seguenti sottoinsiemi dai grafici sopra:

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Chiaramente S ₁ non è un insieme di vertici indipendente, perché per ottenere un insieme di vertici indipendente, dovrebbero esserci almeno due vertici nel da un grafo. Ma qui non è così. I sottoinsiemi S ₂ , S ₃ e S ₄ sono gli insiemi di vertici indipendenti perché non vi è alcun vertice adiacente a uno qualsiasi dei vertici dei sottoinsiemi.

Maximal Independent Vertex Set

Sia "G" un grafo, allora un insieme di vertici indipendente di "G" si dice che sia massimo se nessun altro vertice di "G" può essere aggiunto a "S".

Example

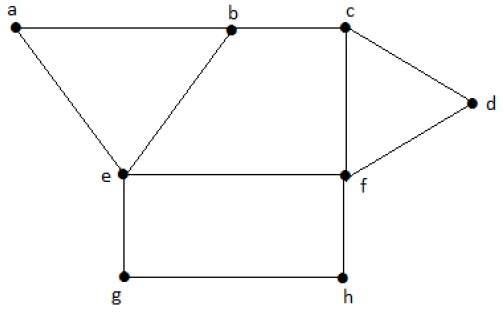
Considera i seguenti sottoinsiemi dai grafici sopra.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ e S ₃ sono i massimi insiemi di vertici indipendenti di "G". In S ₁ e S ₄ , possiamo aggiungere altri vertici; ma in S ₂ e S ₃ , non possiamo aggiungere nessun altro vertice.

Set massimo di vertici indipendenti

Un massimo insieme di vertici indipendenti di 'G' con il numero massimo di vertici è chiamato come il massimo insieme di vertici indipendenti.

Example

Considera i seguenti sottoinsiemi dal grafico sopra:

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Solo S ₃ è il massimo insieme di vertici indipendenti, poiché copre il numero più alto di vertici. Il numero di vertici in un massimo insieme di vertici indipendenti di 'G' è chiamato il numero di vertici indipendenti di G (β ₂ ).

Example

Per il grafico completo K _n ,

Numero di copertura del vertice = α ₂ = n − 1

Numero indipendente dal vertice = β ₂ = 1

Hai α ₂ + β ₂ = n

In un grafo completo, ogni vertice è adiacente ai suoi rimanenti (n - 1) vertici. Pertanto, un insieme massimo indipendente di K _n contiene solo un vertice.

Pertanto, β ₂ = 1

e α ₂ = | v | - β ₂ = n-1

Note - Per qualsiasi grafico 'G' = (V, E)

• α ₂ + β ₂ = | v |
• Se 'S' è un insieme di vertici indipendente di 'G', allora (V - S) è una copertura di vertici di G.