Teoria dei grafi - Guida rapida
Nel dominio della matematica e dell'informatica, la teoria dei grafi è lo studio dei grafi che riguarda la relazione tra archi e vertici . È un argomento popolare che ha le sue applicazioni in informatica, tecnologia dell'informazione, bioscienze, matematica e linguistica per citarne alcuni. Senza ulteriori indugi, iniziamo con la definizione di un grafico.
Cos'è un grafico?
Un grafico è una rappresentazione pittorica di un insieme di oggetti in cui alcune coppie di oggetti sono collegate da collegamenti. Gli oggetti interconnessi sono rappresentati da punti denominati comeverticese vengono chiamati i collegamenti che collegano i vertici edges.
Formalmente, un grafico è una coppia di insiemi (V, E), dove Vè l'insieme dei vertici ed E è l'insieme degli archi, che collega le coppie di vertici. Dai un'occhiata al grafico seguente:
Nel grafico sopra,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
Applicazioni della teoria dei grafi
La teoria dei grafi ha le sue applicazioni in diversi campi dell'ingegneria:
Electrical Engineering- I concetti della teoria dei grafi sono ampiamente utilizzati nella progettazione delle connessioni dei circuiti. I tipi o l'organizzazione delle connessioni sono denominati topologie. Alcuni esempi di topologie sono topologie a stella, bridge, serie e parallela.
Computer Science- La teoria dei grafi viene utilizzata per lo studio degli algoritmi. Per esempio,
- Algoritmo di Kruskal
- Algoritmo di Prim
- Algoritmo di Dijkstra
Computer Network - Le relazioni tra i computer interconnessi nella rete seguono i principi della teoria dei grafi.
Science - La struttura molecolare e chimica di una sostanza, la struttura del DNA di un organismo, ecc. Sono rappresentate da grafici.
Linguistics - L'albero di analisi di una lingua e la grammatica di una lingua utilizzano grafici.
General- I percorsi tra le città possono essere rappresentati utilizzando grafici. La rappresentazione di informazioni ordinate gerarchicamente come l'albero genealogico può essere utilizzata come un tipo speciale di grafico chiamato albero.
Un grafico è un diagramma di punti e linee collegati ai punti. Ha almeno una linea che unisce un insieme di due vertici senza vertici che si connettono. Il concetto di grafi nella teoria dei grafi si basa su alcuni termini di base come punto, linea, vertice, bordo, grado di vertici, proprietà dei grafi, ecc. Qui, in questo capitolo, tratteremo questi fondamenti della teoria dei grafi.
Punto
A pointè una posizione particolare in uno spazio unidimensionale, bidimensionale o tridimensionale. Per una migliore comprensione, un punto può essere indicato da un alfabeto. Può essere rappresentato con un punto.
Esempio

Qui, il punto è un punto chiamato "a".
Linea
UN Lineè una connessione tra due punti. Può essere rappresentato con una linea continua.
Example

Qui, "a" e "b" sono i punti. Il collegamento tra questi due punti è chiamato linea.
Vertice
Un vertice è un punto in cui si incontrano più linee. È anche chiamato anode. Analogamente ai punti, anche un vertice è indicato da un alfabeto.
Example

Qui, il vertice è denominato con un alfabeto "a".
Bordo
Un bordo è il termine matematico per una linea che collega due vertici. Molti bordi possono essere formati da un singolo vertice. Senza un vertice, un bordo non può essere formato. Deve esserci un vertice iniziale e un vertice finale per un bordo.
Example

Qui, "a" e "b" sono i due vertici e il collegamento tra di loro è chiamato bordo.
Grafico
Un grafo 'G' è definito come G = (V, E) dove V è un insieme di tutti i vertici ed E è un insieme di tutti gli archi nel grafico.
Example 1

Nell'esempio sopra, ab, ac, cd e bd sono i bordi del grafico. Allo stesso modo, a, b, c e d sono i vertici del grafo.
Example 2
In questo grafico, ci sono quattro vertici a, b, c, e d e quattro bordi ab, ac, ad e cd.
Ciclo continuo
In un grafico, se un bordo viene disegnato dal vertice a se stesso, viene chiamato loop.
Example 1

Nel grafico sopra, V è un vertice per il quale ha un bordo (V, V) che forma un anello.
Example 2

In questo grafico, ci sono due anelli che si formano al vertice a e al vertice b.
Grado di vertice
È il numero di vertici adiacenti a un vertice V.
Notation - gradi (V).
In un grafo semplice con n numero di vertici, il grado di ogni vertice è -
deg (v) ≤ n - 1 ∀ v ∈ G
Un vertice può formare un bordo con tutti gli altri vertici tranne che da solo. Quindi il grado di un vertice sarà fino anumber of vertices in the graph minus 1. Questo 1 è per l'auto-vertice in quanto non può formare un ciclo da solo. Se è presente un ciclo in uno qualsiasi dei vertici, non è un grafico semplice.
Il grado di vertice può essere considerato in due casi di grafici:
Grafico non diretto
Grafico diretto
Grado di vertice in un grafico non orientato
Un grafo non orientato non ha bordi diretti. Considera i seguenti esempi.
Example 1
Dai un'occhiata al grafico seguente:

Nel grafico non orientato sopra,
deg (a) = 2, poiché ci sono 2 archi che si incontrano al vertice 'a'.
deg (b) = 3, poiché ci sono 3 archi che si incontrano al vertice 'b'.
deg (c) = 1, in quanto vi è 1 bordo formato al vertice 'c'
Quindi "c" è un file pendent vertex.
deg (d) = 2, poiché ci sono 2 archi che si incontrano al vertice 'd'.
deg (e) = 0, poiché ci sono 0 archi formati al vertice 'e'.
Quindi "e" è un file isolated vertex.
Example 2
Dai un'occhiata al grafico seguente:

Nel grafico sopra,
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 e deg (e) = 0.
Il vertice "e" è un vertice isolato. Il grafico non ha vertici pendenti.
Grado di vertice in un grafico orientato
In un grafo diretto, ogni vertice ha un'estensione indegree e un outdegree.
Indegree of a Graph
L'indice del vertice V è il numero di bordi che entrano nel vertice V.
Notation - deg− (V).
Fuori grado di un grafico
Fuori grado del vertice V è il numero di archi che escono dal vertice V.
Notation - gradi + (V).
Considera i seguenti esempi.
Example 1
Dai un'occhiata al seguente grafico diretto. Il vertice "a" ha due bordi, "ad" e "ab", che vanno verso l'esterno. Quindi il suo grado esterno è 2. Allo stesso modo, c'è un bordo "ga", che viene verso il vertice "a". Quindi l'indice di "a" è 1.

L'indegree e il outdegree degli altri vertici sono mostrati nella tabella seguente:
| Vertice | Indegree | Outdegree |
|---|---|---|
| un | 1 | 2 |
| b | 2 | 0 |
| c | 2 | 1 |
| d | 1 | 1 |
| e | 1 | 1 |
| f | 1 | 1 |
| g | 0 | 2 |
Example 2
Dai un'occhiata al seguente grafico diretto. Il vertice "a" ha un bordo "ae" che va verso l'esterno dal vertice "a". Quindi il suo grado esterno è 1. Allo stesso modo, il grafico ha un bordo "ba" che va verso il vertice "a". Quindi l'indice di "a" è 1.

L'indegree e il outdegree degli altri vertici sono mostrati nella tabella seguente:
| Vertice | Indegree | Outdegree |
|---|---|---|
| un | 1 | 1 |
| b | 0 | 2 |
| c | 2 | 0 |
| d | 1 | 1 |
| e | 1 | 1 |
Vertice pendente
Usando il grado di un vertice, abbiamo due tipi speciali di vertici. Un vertice di grado uno è chiamato vertice pendente.
Example

Qui, in questo esempio, il vertice "a" e il vertice "b" hanno un bordo connesso "ab". Quindi rispetto al vertice "a" c'è un solo spigolo verso il vertice "b" e analogamente rispetto al vertice "b" c'è un solo spigolo verso il vertice "a". Infine, il vertice "a" e il vertice "b" hanno un grado che è anche chiamato vertice pendente.
Vertice isolato
Un vertice con grado zero è chiamato vertice isolato.
Example

Qui, il vertice "a" e il vertice "b" non hanno connettività tra loro e anche con altri vertici. Quindi il grado di entrambi i vertici "a" e "b" è zero. Questi sono anche chiamati vertici isolati.
Adiacenza
Ecco le norme di adiacenza -
In un grafo, si dice che siano due vertici adjacent, se è presente un bordo tra i due vertici. Qui, l'adiacenza dei vertici è mantenuta dal singolo bordo che collega quei due vertici.
In un grafico, si dice che due bordi sono adiacenti, se c'è un vertice comune tra i due bordi. Qui, l'adiacenza degli spigoli è mantenuta dal singolo vertice che collega due spigoli.
Example 1
Nel grafico sopra -
'a' e 'b' sono i vertici adiacenti, poiché tra di loro c'è un bordo comune 'ab'.
'a' e 'd' sono i vertici adiacenti, poiché tra di loro c'è un bordo comune 'ad'.
ab 'e' be 'sono i bordi adiacenti, poiché tra loro c'è un vertice comune' b '.
be 'e' de 'sono gli spigoli adiacenti, poiché tra loro c'è un vertice comune' e '.
Example 2
Nel grafico sopra -
'a' e 'd' sono i vertici adiacenti, poiché tra di loro c'è un bordo comune 'ad'.
"c" e "b" sono i vertici adiacenti, poiché tra loro c'è un bordo comune "cb".
"ad" e "cd" sono i bordi adiacenti, poiché tra di loro c'è un vertice comune "d".
"ac" e "cd" sono i bordi adiacenti, poiché tra di loro c'è un vertice comune "c".
Bordi paralleli
In un grafico, se una coppia di vertici è collegata da più di un bordo, questi sono chiamati bordi paralleli.
Nel grafico sopra, "a" e "b" sono i due vertici collegati tra loro da due spigoli "ab" e "ab". Quindi è chiamato come un bordo parallelo.
Multi grafico
Un grafico con bordi paralleli è noto come Multigraph.
Example 1

Nel grafico sopra, ci sono cinque bordi "ab", "ac", "cd", "cd" e "bd". Poiché "c" e "d" hanno due bordi paralleli tra loro, è un Multigraph.
Example 2
Nel grafico sopra, i vertici "b" e "c" hanno due bordi. Anche i vertici "e" e "d" hanno due bordi tra loro. Quindi è un Multigraph.
Sequenza dei gradi di un grafico
Se i gradi di tutti i vertici in un grafico sono disposti in ordine decrescente o crescente, la sequenza ottenuta è nota come sequenza di gradi del grafico.
Example 1

| Vertice | UN | b | c | d | e |
|---|---|---|---|---|---|
| Connessione a | avanti Cristo | anno Domini | anno Domini | c, b, e | d |
| Grado | 2 | 2 | 2 | 3 | 1 |
Nel grafico sopra, per i vertici {d, a, b, c, e}, la sequenza dei gradi è {3, 2, 2, 2, 1}.
Example 2

| Vertice | UN | b | c | d | e | f |
|---|---|---|---|---|---|---|
| Connessione a | essere | corrente alternata | b, d | c, e | anno Domini | - |
| Grado | 2 | 2 | 2 | 2 | 2 | 0 |
Nel grafico sopra, per i vertici {a, b, c, d, e, f}, la sequenza dei gradi è {2, 2, 2, 2, 2, 0}.
I grafici sono dotati di varie proprietà che vengono utilizzate per la caratterizzazione dei grafici a seconda delle loro strutture. Queste proprietà sono definite in termini specifici pertinenti al dominio della teoria dei grafi. In questo capitolo, discuteremo alcune proprietà di base comuni a tutti i grafici.
Distanza tra due vertici
È il numero di bordi in un percorso più breve tra il vertice U e il vertice V. Se sono presenti più percorsi che collegano due vertici, il percorso più breve è considerato come la distanza tra i due vertici.
Notazione - d (U, V)
Può essere presente un numero qualsiasi di percorsi da un vertice all'altro. Tra questi, devi scegliere solo quello più corto.
Example
Dai un'occhiata al grafico seguente:

Qui, la distanza dal vertice "d" al vertice "e" o semplicemente "de" è 1 poiché c'è un bordo tra di loro. Ci sono molti percorsi dal vertice 'd' al vertice 'e' -
- da, ab, be
- df, fg, ge
- de (è considerato per la distanza tra i vertici)
- df, fc, ca, ab, be
- da, ac, cf, fg, ge
Eccentricità di un vertice
La distanza massima tra un vertice e tutti gli altri vertici è considerata come l'eccentricità del vertice.
Notazione - e (V)
Viene presa la distanza da un particolare vertice a tutti gli altri vertici nel grafico e tra quelle distanze, l'eccentricità è la più alta delle distanze.
Example
Nel grafico sopra, l'eccentricità di "a" è 3.
La distanza da "a" a "b" è 1 ("ab"),
da 'a' a 'c' è 1 ('ac'),
da "a" a "d" è 1 ("annuncio"),
da 'a' a 'e' è 2 ('ab' - 'be') o ('ad' - 'de'),
da 'a' a 'f' è 2 ('ac' - 'cf') o ('ad' - 'df'),
da 'a' a 'g' è 3 ('ac' - 'cf' - 'fg') o ('ad' - 'df' - 'fg').
Quindi l'eccentricità è 3, che è un massimo dal vertice "a" dalla distanza tra "ag" che è massimo.
In altre parole,
e (b) = 3
e (c) = 3
e (d) = 2
e (e) = 3
e (f) = 3
e (g) = 3
Raggio di un grafico connesso
L'eccentricità minima da tutti i vertici è considerata come il raggio del grafico G. La minima tra tutte le distanze massime tra un vertice e tutti gli altri vertici è considerata come il raggio del grafico G.
Notazione - r (G)
Da tutte le eccentricità dei vertici in un grafo, il raggio del grafo connesso è il minimo di tutte quelle eccentricità.
Example
Nel grafico sopra r (G) = 2, che è l'eccentricità minima per 'd'.
Diametro di un grafico
L'eccentricità massima da tutti i vertici è considerata come il diametro del grafico G. Il massimo tra tutte le distanze tra un vertice e tutti gli altri vertici è considerato come il diametro del grafico G.
Notation − d(G) - Da tutte le eccentricità dei vertici in un grafo, il diametro del grafo connesso è il massimo di tutte quelle eccentricità.
Example
Nel grafico sopra, d (G) = 3; che è la massima eccentricità.
Punto centrale
Se l'eccentricità di un grafico è uguale al suo raggio, allora è noto come il punto centrale del grafico. Se
e (V) = r (V),
quindi "V" è il punto centrale del grafico "G".
Example
Nel grafico di esempio, "d" è il punto centrale del grafico.
e (d) = r (d) = 2
Centro
L'insieme di tutti i punti centrali di "G" è chiamato il centro del grafico.
Example
Nel grafico di esempio, {'d'} è il centro del grafico.
Circonferenza
Il number of edges in the longest cycle of ‘G’ è chiamato come la circonferenza di 'G'.
Example
Nel grafico di esempio, la circonferenza è 6, che abbiamo derivato dal ciclo più lungo acfgeba o acfdeba.
Circonferenza
Il numero di bordi nel ciclo più breve di "G" è chiamato circonferenza.
Notation: g (G).
Example - Nel grafico di esempio, la circonferenza del grafico è 4, che abbiamo derivato dal ciclo più breve acfda o dfged o abeda.
Teorema della somma dei gradi dei vertici
Se G = (V, E) è un grafo non diretto con vertici V = {V 1 , V 2 ,… V n } allora
Corollary 1
Se G = (V, E) è un grafo orientato con vertici V = {V 1 , V 2 ,… V n }, allora
Corollary 2
In qualsiasi grafo non diretto, il numero di vertici con grado dispari è pari.
Corollary 3
In un grafo non diretto, se il grado di ogni vertice è k, allora
Corollary 4
In un grafo non diretto, se il grado di ciascun vertice è almeno k, allora
| Corollary 5
In un grafo non diretto, se il grado di ogni vertice è al massimo k, allora
Esistono vari tipi di grafici a seconda del numero di vertici, del numero di bordi, dell'interconnettività e della loro struttura complessiva. In questo capitolo discuteremo solo alcuni importanti tipi di grafici.
Grafico nullo
A graph having no edges è chiamato un grafico nullo.
Esempio

Nel grafico sopra, ci sono tre vertici denominati "a", "b" e "c", ma non ci sono bordi tra di loro. Quindi è un grafico nullo.
Grafico banale
UN graph with only one vertex è chiamato Trivial Graph.
Esempio

Nel grafico mostrato sopra, c'è solo un vertice "a" senza altri bordi. Quindi è un grafico banale.
Grafico non orientato
Un grafo non diretto contiene bordi ma i bordi non sono quelli diretti.
Esempio
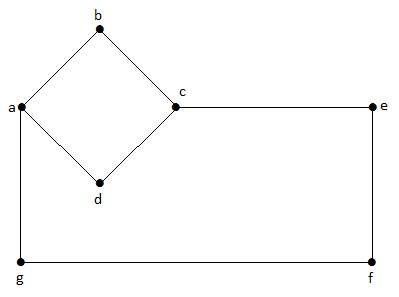
In questo grafico, "a", "b", "c", "d", "e", "f", "g" sono i vertici e "ab", "bc", "cd", "da ',' ag ',' gf ',' ef 'sono i bordi del grafico. Poiché si tratta di un grafico non orientato, i bordi "ab" e "ba" sono gli stessi. Allo stesso modo anche altri bordi considerati allo stesso modo.
Grafico diretto
In un grafico orientato, ogni bordo ha una direzione.
Esempio

Nel grafico sopra, abbiamo sette vertici "a", "b", "c", "d", "e", "f" e "g" e otto spigoli "ab", "cb", " dc "," ad "," ec "," fe "," gf "e" ga ". Trattandosi di un grafico orientato, ogni bordo reca una freccia che ne mostra la direzione. Notare che in un grafo orientato, "ab" è diverso da "ba".
Grafico semplice
Un grafico with no loops e no parallel edges è chiamato un semplice grafico.
Il numero massimo di archi possibile in un singolo grafo con 'n' vertici è n C 2 dove n C 2 = n (n - 1) / 2.
Il numero di grafi semplici possibili con 'n' vertici = 2 n c 2 = 2 n (n-1) / 2 .
Esempio
Nel grafico seguente, ci sono 3 vertici con 3 bordi che è il massimo escludendo i bordi paralleli e gli anelli. Ciò può essere dimostrato utilizzando le formule di cui sopra.
Il numero massimo di archi con n = 3 vertici -
Il numero massimo di grafici semplici con n = 3 vertici -
Questi 8 grafici sono come mostrato di seguito:
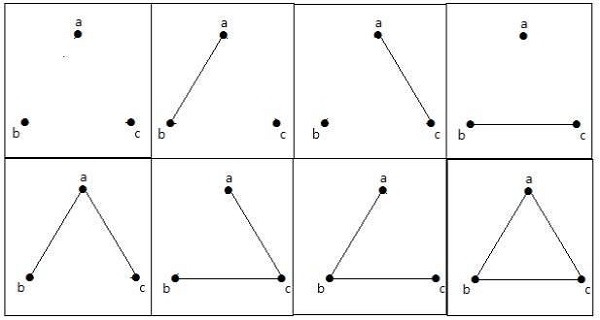
Grafico connesso
Si dice che un grafo G sia connesso if there exists a path between every pair of vertices. Dovrebbe esserci almeno un bordo per ogni vertice nel grafico. Quindi possiamo dire che è collegato a qualche altro vertice sull'altro lato del bordo.
Esempio
Nel grafico seguente, ogni vertice ha il proprio bordo connesso all'altro bordo. Quindi è un grafico connesso.

Grafico disconnesso
Un grafo G è disconnesso, se non contiene almeno due vertici collegati.
Esempio 1
Il grafico seguente è un esempio di un grafico disconnesso, in cui sono presenti due componenti, uno con vertici 'a', 'b', 'c', 'd' e un altro con 'e', 'f', 'g', vertici 'h'.
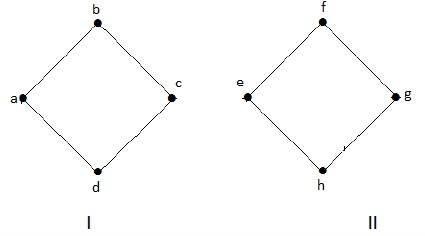
I due componenti sono indipendenti e non collegati tra loro. Quindi è chiamato grafico disconnesso.
Esempio 2

In questo esempio, ci sono due componenti indipendenti, abfe e cd, che non sono collegati tra loro. Quindi questo è un grafico disconnesso.
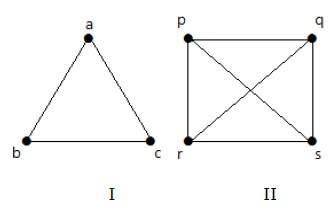
Grafico regolare
Si dice che un grafico G sia regolare, if all its vertices have the same degree. In un grafico, se il grado di ciascun vertice è "k", il grafico viene chiamato "grafo k-regolare".
Esempio
Nei grafici seguenti, tutti i vertici hanno lo stesso grado. Quindi questi grafici sono chiamati grafici regolari.
In entrambi i grafici, tutti i vertici hanno grado 2. Sono chiamati 2-Regular Graphs.
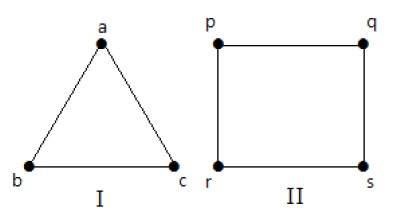
Grafico completo
Un semplice grafo con 'n' vertici reciproci è chiamato grafo completo e lo è denoted by ‘Kn’. Nel grafico,a vertex should have edges with all other vertices, quindi ha chiamato un grafico completo.
In altre parole, se un vertice è connesso a tutti gli altri vertici in un grafo, allora viene chiamato grafo completo.
Esempio
Nei grafici seguenti, ogni vertice del grafo è connesso a tutti i rimanenti vertici del grafo tranne che da solo.
Nel grafico I,
| un | b | c | |
|---|---|---|---|
| un | Non collegata | Collegato | Collegato |
| b | Collegato | Non collegata | Collegato |
| c | Collegato | Collegato | Non collegata |
Nel grafico II,
| p | q | r | S | |
|---|---|---|---|---|
| p | Non collegata | Collegato | Collegato | Collegato |
| q | Collegato | Non collegata | Collegato | Collegato |
| r | Collegato | Collegato | Non collegata | Collegato |
| S | Collegato | Collegato | Collegato | Non collegata |
Grafico del ciclo
Un grafo semplice con vertici "n" (n> = 3) e archi "n" è chiamato grafo a ciclo se tutti i suoi archi formano un ciclo di lunghezza "n".
Se il grado di ciascun vertice nel grafico è due, viene chiamato grafico del ciclo.
Notation- C n
Esempio
Dai un'occhiata ai seguenti grafici:
Il grafico I ha 3 vertici con 3 bordi che formano un ciclo "ab-bc-ca".
Il grafico II ha 4 vertici con 4 bordi che formano un ciclo 'pq-qs-sr-rp'.
Il grafico III ha 5 vertici con 5 bordi che formano un ciclo "ik-km-ml-lj-ji".

Quindi tutti i grafici dati sono grafici di ciclo.
Grafico ruota
Un grafico della ruota è ottenuto da un grafico del ciclo C n-1 aggiungendo un nuovo vertice. Quel nuovo vertice è chiamato aHubche è connesso a tutti i vertici di C n .
Notazione - W n
N. di spigoli in W n = N. di spigoli dal mozzo a tutti gli altri vertici +
Numero di bordi da tutti gli altri nodi nel grafico del ciclo senza hub.
= (n – 1) + (n – 1)
= 2 (n – 1)
Esempio
Dai un'occhiata ai grafici seguenti. Sono tutti grafici delle ruote.
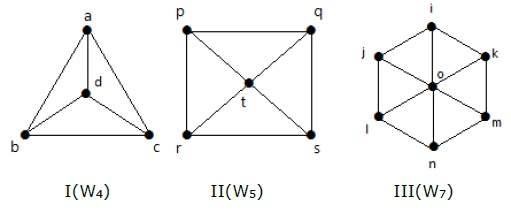
Nel grafico I, si ottiene da C 3 aggiungendo un vertice al centro denominato "d". È indicato come W 4 .
Numero di bordi in W4 = 2 (n-1) = 2 (3) = 6
Nel grafico II, si ottiene da C4 aggiungendo un vertice al centro denominato "t". È indicato come W 5 .
Numero di spigoli in W5 = 2 (n-1) = 2 (4) = 8
Nel grafico III, si ottiene da C 6 aggiungendo un vertice al centro denominato "o". È indicato come W 7 .
Numero di bordi in W4 = 2 (n-1) = 2 (6) = 12
Grafico ciclico
Un grafico with at least one ciclo è chiamato un grafico ciclico.
Esempio
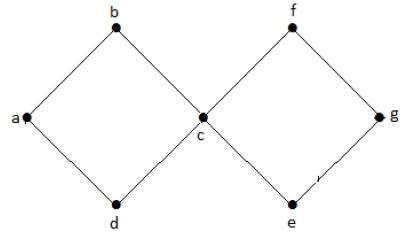
Nel grafico di esempio sopra, abbiamo due cicli abcda e cfgec. Quindi è chiamato un grafico ciclico.
Grafico aciclico
Un grafico with no cycles è chiamato grafo aciclico.
Esempio
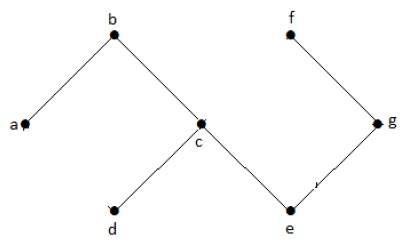
Nel grafico di esempio sopra, non abbiamo cicli. Quindi è un grafico non ciclico.
Grafico bipartito
Un semplice grafo G = (V, E) con partizione di vertice V = {V 1 , V 2 } è chiamato grafo bipartitoif every edge of E joins a vertex in V1 to a vertex in V2.
In generale, un grafo Bipertite ha due insiemi di vertici, diciamo V1 e V2, e se viene disegnato un bordo, dovrebbe connettere qualsiasi vertice nell'insieme V 1 a qualsiasi vertice nell'insieme V 2 .
Esempio
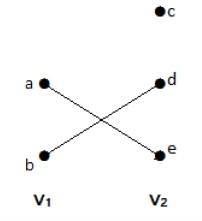
In questo grafico, puoi osservare due insiemi di vertici: V 1 e V 2 . Qui, due archi denominati "ae" e "bd" collegano i vertici di due insiemi V 1 e V 2 .
Grafico bipartito completo
Un grafo bipartito 'G', G = (V, E) con partizione V = {V 1 , V 2 } si dice che sia un grafo bipartito completo se ogni vertice in V 1 è connesso a ogni vertice di V 2 .
In generale, un grafo bipartito completo collega ogni vertice dell'insieme V 1 a ciascun vertice dell'insieme V 2 .
Esempio
Il seguente grafico è un grafo bipartito completo perché ha archi che collegano ogni vertice dell'insieme V 1 a ciascun vertice dell'insieme V 2 .
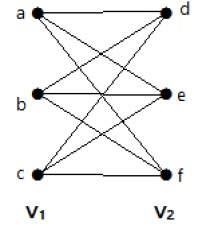
Se | V 1 | = me | V 2 | = n, allora il grafo bipartito completo è indicato con K m, n .
- K m, n ha (m + n) vertici e (mn) bordi.
- K m, n è un grafo regolare se m = n.
In generale, a complete bipartite graph is not a complete graph.
K m, n è un grafico completo se m = n = 1.
Il numero massimo di archi in un grafo bipartito con n vertici è -
[n 2 /4]
Se n = 10, k5, 5 = [n2 / 4] = [10 2 /4] = 25.
Allo stesso modo, K6, 4 = 24
K7, 3 = 21
K8, 2 = 16
K9, 1 = 9
Se n = 9, k5, 4 = [n2 / 4] = [92/4] = 20
Allo stesso modo, K6, 3 = 18
K7, 2 = 14
K8, 1 = 8
"G" è un grafo bipartito se "G" non ha cicli di lunghezza dispari. Un caso speciale di grafo bipartito è un grafo a stella.
Grafico a stella
Un grafo bipartito completo della forma K1, n-1 è un grafo stellare con n vertici. Un grafo a stella è un grafo bipartito completo se un singolo vertice appartiene a un insieme e tutti i vertici rimanenti appartengono all'altro insieme.
Esempio
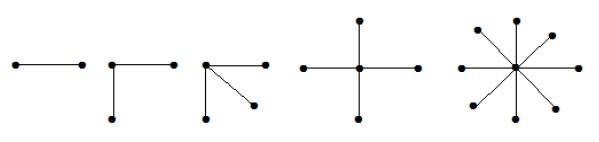
Nei grafici precedenti, su "n" vertici, tutti i vertici "n – 1" sono collegati a un singolo vertice. Quindi è nella forma di K 1 , n-1 che sono grafici stellari.
Complemento di un grafico
Sia 'G−' un grafo semplice con alcuni vertici come quello di 'G' e uno spigolo {U, V} è presente in 'G−', se lo spigolo non è presente in G. Significa che due vertici sono adiacenti in 'G−' se i due vertici non sono adiacenti in G.
Se gli archi che esistono nel grafico I sono assenti in un altro grafico II, e se sia il grafico I che il grafico II sono combinati insieme per formare un grafico completo, allora il grafico I e il grafico II sono chiamati complementi l'uno dell'altro.
Esempio
Nell'esempio seguente, graph-I ha due bordi "cd" e "bd". Il suo grafo del complemento-II ha quattro bordi.
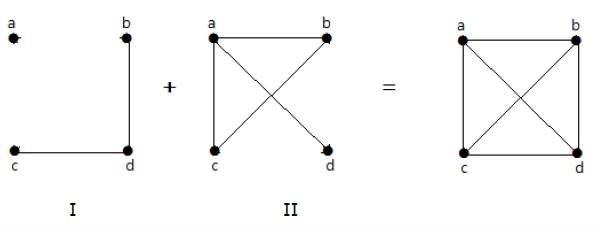
Si noti che gli archi nel grafo-I non sono presenti nel grafo-II e viceversa. Quindi, la combinazione di entrambi i grafici fornisce un grafo completo di "n" vertici.
Note - Una combinazione di due grafici complementari fornisce un grafico completo.
Se "G" è un grafico semplice, allora
| E (G) | + | E ('G -') | = | E (Kn) |, dove n = numero di vertici nel grafo.
Esempio
Sia "G" un grafo semplice con nove vertici e dodici archi, trova il numero di archi in "G-".
Hai, | E (G) | + | E ('G -') | = | E (Kn) |
12 + | E ('Sol -') | =
9 (9-1) / 2 = 9 C 2
12 + | E ('Sol -') | = 36
| E ('G -') | = 24
"G" è un grafico semplice con 40 archi e il suo complemento "G−" ha 38 archi. Trova il numero di vertici nel grafo G o 'G−'.
Lascia che il numero di vertici nel grafo sia "n".
Abbiamo, | E (G) | + | E ('G -') | = | E (Kn) |
40 + 38 = n (n-1) / 2
156 = n (n-1)
13 (12) = n (n-1)
n = 13
Gli alberi sono grafici che non contengono nemmeno un singolo ciclo. Rappresentano la struttura gerarchica in forma grafica. Gli alberi appartengono alla classe di grafici più semplice. Nonostante la loro semplicità, hanno una struttura ricca.
Gli alberi forniscono una gamma di applicazioni utili da semplici come un albero genealogico a complesse come alberi nelle strutture dati dell'informatica.
Albero
UN connected acyclic graphsi chiama albero. In altre parole, un grafo connesso senza cicli è chiamato albero.
I bordi di un albero sono noti come branches. Gli elementi degli alberi sono chiamati i loro nodi. Vengono chiamati i nodi senza nodi figlioleaf nodes.
Un albero con vertici "n" ha bordi "n-1". Se ha un bordo in più rispetto a 'n-1', allora il bordo extra dovrebbe ovviamente accoppiarsi con due vertici che portano a formare un ciclo. Quindi, diventa un grafico ciclico che è una violazione per il grafico ad albero.
Example 1
Il grafico mostrato qui è un albero perché non ha cicli ed è connesso. Ha quattro vertici e tre bordi, cioè per 'n' vertici bordi 'n-1' come menzionato nella definizione.
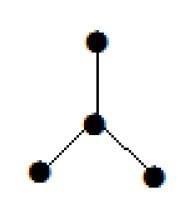
Note - Ogni albero ha almeno due vertici di primo grado.
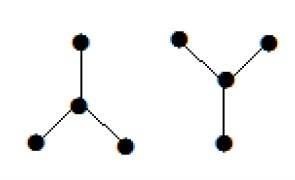
Example 2
Nell'esempio sopra, i vertici "a" e "d" hanno il grado uno. E gli altri due vertici "b" e "c" hanno il grado due. Ciò è possibile perché per non formare un ciclo, dovrebbero esserci almeno due bordi singoli ovunque nel grafico. Non è altro che due bordi con un grado di uno.
foresta
UN disconnected acyclic graphsi chiama foresta. In altre parole, una raccolta disgiunta di alberi è chiamata foresta.
Example
Il grafico seguente assomiglia a due sottografi; ma è un unico grafo disconnesso. Non ci sono cicli in questo grafico. Quindi, chiaramente è una foresta.
Spanning Trees
Sia G un grafo connesso, allora il sottografo H di G è chiamato spanning tree di G se -
- H è un albero
- H contiene tutti i vertici di G.
Uno spanning tree T di un grafo non orientato G è un sottografo che include tutti i vertici di G.
Example

Nell'esempio sopra, G è un grafo connesso e H è un sottografo di G.
Chiaramente, il grafo H non ha cicli, è un albero con sei spigoli che è uno in meno del numero totale di vertici. Quindi H è lo Spanning tree di G.
Classifica del circuito
Sia 'G' un grafo connesso con 'n' vertici e bordi 'm'. Uno spanning tree 'T' di G contiene (n-1) archi.
Pertanto, il numero di archi che è necessario eliminare da "G" per ottenere uno spanning tree = m- (n-1), che è chiamato rango del circuito di G.
Questa formula è vera, perché in uno spanning tree è necessario avere bordi "n-1". Fuori dagli archi 'm', è necessario mantenere gli archi 'n – 1' nel grafico.
Quindi, cancellando 'n – 1' archi da 'm' si ottengono gli archi da rimuovere dal grafico per ottenere uno spanning tree, che non dovrebbe formare un ciclo.
Example
Dai un'occhiata al grafico seguente:
Per il grafico dato nell'esempio sopra, hai m = 7 spigoli en = 5 vertici.
Quindi la classifica del circuito è -
Example
Sia 'G' un grafo connesso con sei vertici e il grado di ogni vertice è tre. Trova il rango del circuito "G".
Per la somma del teorema del grado dei vertici,
Teorema di Kirchoff
Il teorema di Kirchoff è utile per trovare il numero di spanning tree che possono essere formati da un grafo connesso.
Example
La matrice "A" deve essere riempita come se ci fosse un bordo tra due vertici, allora dovrebbe essere data come "1", altrimenti "0".
$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$Usando il teorema di Kirchoff, dovrebbe essere modificato sostituendo i valori diagonali principali con il grado dei vertici e tutti gli altri elementi con -1.A
$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$Pertanto, il numero di spanning tree = 8.
Se è possibile attraversare un grafico da un vertice all'altro è determinato dal modo in cui un grafico è connesso. La connettività è un concetto di base nella teoria dei grafi. La connettività definisce se un grafico è connesso o disconnesso. Ha argomenti secondari basati su bordo e vertice, noti come connettività edge e connettività vertice. Cerchiamo di discuterli in dettaglio.
Connettività
Si dice che sia un grafico connected if there is a path between every pair of vertex. Da ogni vertice a qualsiasi altro vertice, dovrebbe esserci un percorso da attraversare. Questa è chiamata connettività di un grafico. Si dice che un grafo con più vertici e bordi scollegati sia disconnesso.
Example 1
Nel grafico seguente, è possibile viaggiare da un vertice a qualsiasi altro vertice. Ad esempio, si può passare dal vertice "a" al vertice "e" utilizzando il percorso "ab-e".
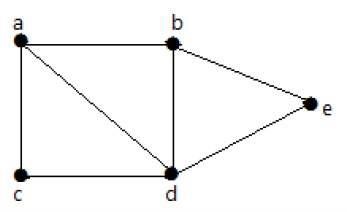
Example 2
Nell'esempio seguente, l'attraversamento dal vertice "a" al vertice "f" non è possibile perché non esiste alcun percorso tra di loro direttamente o indirettamente. Quindi è un grafico disconnesso.
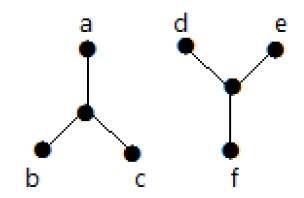
Cut Vertex
Sia "G" un grafo connesso. Un vertice V ∈ G è chiamato vertice tagliato di 'G', se 'G-V' (Elimina 'V' da 'G') risulta in un grafo disconnesso. La rimozione di un vertice tagliato da un grafico lo suddivide in due o più grafici.
Note - La rimozione di un vertice tagliato può rendere un grafico scollegato.
Un grafo connesso 'G' può avere al massimo (n – 2) vertici tagliati.
Example
Nel grafico seguente, i vertici "e" e "c" sono i vertici tagliati.

Rimuovendo "e" o "c", il grafico diventerà un grafico disconnesso.

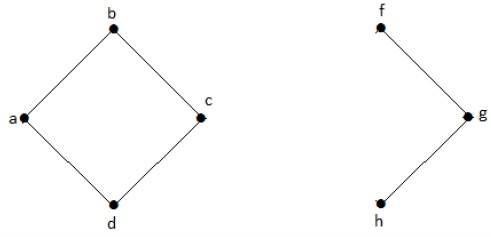
Senza 'g', non c'è percorso tra il vertice 'c' e il vertice 'h' e molti altri. Quindi è un grafo disconnesso con vertice tagliato come "e". Allo stesso modo, 'c' è anche un vertice tagliato per il grafico sopra.
Bordo tagliato (ponte)
Sia "G" un grafo connesso. Un arco 'e' ∈ G è detto bordo tagliato se 'G-e' risulta in un grafo disconnesso.
Se rimuovendo un bordo in un grafico si ottengono due o più grafici, quel bordo viene chiamato bordo tagliato.
Example
Nel grafico seguente, il bordo tagliato è [(c, e)].

Rimuovendo il bordo (c, e) dal grafico, diventa un grafico disconnesso.


Nel grafico sopra, la rimozione del bordo (c, e) spezza il grafico in due che non è altro che un grafico disconnesso. Quindi, il bordo (c, e) è un bordo tagliato del grafico.
Note - Sia 'G' un grafo connesso con 'n' vertici, quindi
un bordo tagliato e ∈ G se e solo se il bordo 'e' non fa parte di alcun ciclo in G.
il numero massimo di bordi tagliati possibile è 'n-1'.
ogniqualvolta esistono bordi tagliati, esistono anche vertici tagliati perché almeno un vertice di un bordo tagliato è un vertice tagliato.
se esiste un vertice tagliato, allora un bordo tagliato può o non può esistere.
Taglia insieme di un grafico
Sia 'G' = (V, E) un grafo connesso. Un sottoinsieme E 'di E è chiamato un insieme tagliato di G se la cancellazione di tutti gli archi di E' da G fa disconnettere G.
Se l'eliminazione di un certo numero di bordi da un grafico ne causa la disconnessione, tali bordi eliminati vengono chiamati il gruppo di tagli del grafico.
Example
Dai un'occhiata al grafico seguente. Il suo set di taglio è E1 = {e1, e3, e5, e8}.
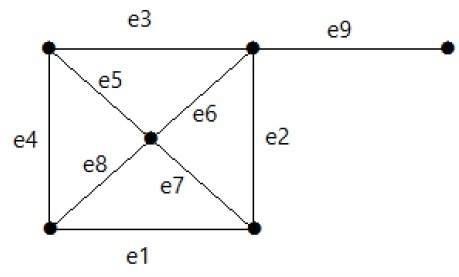
Dopo aver rimosso il set di taglio E1 dal grafico, apparirà come segue:
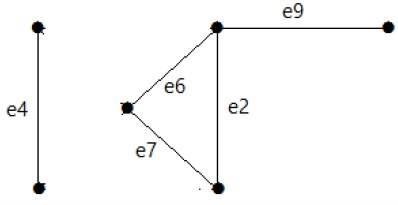
Allo stesso modo, ci sono altri gruppi di taglio che possono disconnettere il grafico -
E3 = {e9} - Il più piccolo insieme di sezioni del grafico.
E4 = {e3, e4, e5}
Connettività Edge
Sia "G" un grafo connesso. Il numero minimo di bordi la cui rimozione rende 'G' scollegato è chiamato connettività degli spigoli di G.
Notation - λ (G)
In altre parole, il file number of edges in a smallest cut set of G è chiamata la connettività edge di G.
Se 'G' ha un bordo tagliato, allora λ (G) è 1. (connettività del bordo di G.)
Example
Dai un'occhiata al grafico seguente. Rimuovendo due bordi minimi, il grafico connesso viene disconnesso. Quindi, la sua connettività di bordo (λ (G)) è 2.
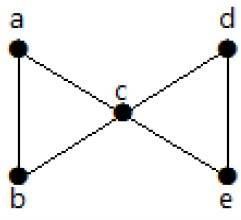
Ecco i quattro modi per scollegare il grafico rimuovendo due bordi:

Vertex Connectivity
Sia "G" un grafo connesso. Il numero minimo di vertici la cui rimozione rende "G" scollegato o riduce "G" a un grafo banale è chiamato la sua connettività di vertice.
Notation - K (G)
Example
Nel grafico sopra, la rimozione dei vertici "e" e "i" rende il grafico scollegato.

Se G ha un vertice tagliato, allora K (G) = 1.
Notation - Per qualsiasi grafo G connesso,
K (G) ≤ λ (G) ≤ δ (G)
Connettività al vertice (K (G)), connettività ai bordi (λ (G)), numero minimo di gradi di G (δ (G)).
Example
Calcola λ (G) e K (G) per il grafico seguente:
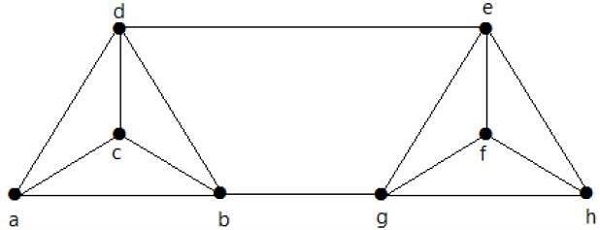
Solution
Dal grafico,
δ (Sol) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
Eliminando i bordi {d, e} e {b, h}, possiamo scollegare G.
Perciò,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
Da (2) e (3), la connettività dei vertici K (G) = 2
Un grafo coprente è un sottografo che contiene tutti i vertici o tutti i bordi corrispondenti a qualche altro grafo. Un sottografo che contiene tutti i vertici è chiamato aline/edge covering. Un sottografo che contiene tutti i bordi è chiamato avertex covering.
Linea di copertura
Sia G = (V, E) un grafico. Un sottoinsieme C (E) è chiamato copertura di linea di G se ogni vertice di G è incidente con almeno un arco in C, cioè,
gradi (V) ≥ 1 ∀ V ∈ G
perché ogni vertice è connesso con un altro vertice da un bordo. Quindi ha un grado minimo di 1.
Example
Dai un'occhiata al grafico seguente:
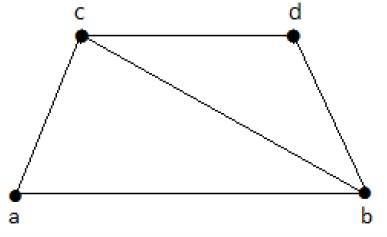
I suoi sottografi con copertura della linea sono i seguenti:
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
La copertura di linea di 'G' non esiste se e solo se 'G' ha un vertice isolato. La copertura di linea di un grafo con 'n' vertici ha almeno [n / 2] bordi.
Copertura minimale
Si dice che una linea che copre C di un grafo G sia minima if no edge can be deleted from C.
Example
Nel grafico sopra, i sottografi che coprono la linea sono i seguenti:
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
Qui, C 1 , C 2 , C 3 sono coperture di linea minime, mentre C 4 non lo è perché possiamo eliminare {b, c}.
Minimum Line Covering
It is also known as Smallest Minimal Line Covering. A minimal line covering with minimum number of edges is called a minimum line covering of ‘G’. The number of edges in a minimum line covering in ‘G’ is called the line covering number of ‘G’ (α1).
Example
In the above example, C1 and C2 are the minimum line covering of G and α1 = 2.
Every line covering contains a minimal line covering.
Every line covering does not contain a minimum line covering (C3 does not contain any minimum line covering.
No minimal line covering contains a cycle.
If a line covering ‘C’ contains no paths of length 3 or more, then ‘C’ is a minimal line covering because all the components of ‘C’ are star graph and from a star graph, no edge can be deleted.
Vertex Covering
Let ‘G’ = (V, E) be a graph. A subset K of V is called a vertex covering of ‘G’, if every edge of ‘G’ is incident with or covered by a vertex in ‘K’.
Example
Take a look at the following graph −
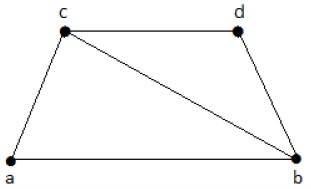
The subgraphs that can be derived from the above graph are as follows −
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
K4 = {a, d}
Here, K1, K2, and K3 have vertex covering, whereas K4 does not have any vertex covering as it does not cover the edge {bc}.
Minimal Vertex Covering
A vertex ‘K’ of graph ‘G’ is said to be minimal vertex covering if no vertex can be deleted from ‘K’.
Example
In the above graph, the subgraphs having vertex covering are as follows −
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
Here, K1 and K2 are minimal vertex coverings, whereas in K3, vertex ‘d’ can be deleted.
Minimum Vertex Covering
It is also known as the smallest minimal vertex covering. A minimal vertex covering of graph ‘G’ with minimum number of vertices is called the minimum vertex covering.
The number of vertices in a minimum vertex covering of ‘G’ is called the vertex covering number of G (α2).
Example
In the following graph, the subgraphs having vertex covering are as follows −
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}

Here, K1 is a minimum vertex cover of G, as it has only two vertices. α2 = 2.
A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Simply, there should not be any common vertex between any two edges.
Matching
Let ‘G’ = (V, E) be a graph. A subgraph is called a matching M(G), if each vertex of G is incident with at most one edge in M, i.e.,
deg(V) ≤ 1 ∀ V ∈ G
which means in the matching graph M(G), the vertices should have a degree of 1 or 0, where the edges should be incident from the graph G.
Notation − M(G)
Example
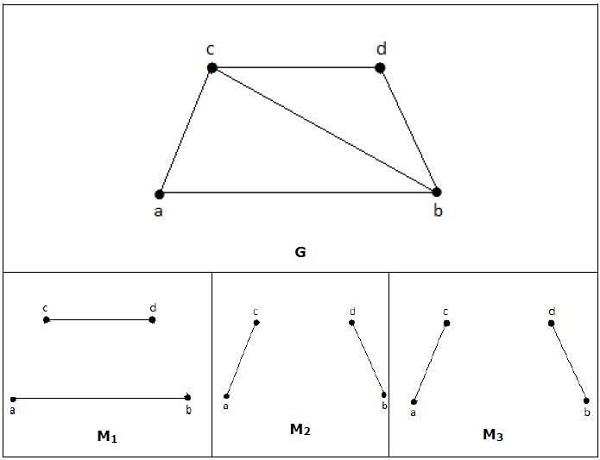

In a matching,
if deg(V) = 1, then (V) is said to be matched
if deg(V) = 0, then (V) is not matched.
In a matching, no two edges are adjacent. It is because if any two edges are adjacent, then the degree of the vertex which is joining those two edges will have a degree of 2 which violates the matching rule.
Maximal Matching
A matching M of graph ‘G’ is said to maximal if no other edges of ‘G’ can be added to M.
Example

M1, M2, M3 from the above graph are the maximal matching of G.
Maximum Matching
It is also known as largest maximal matching. Maximum matching is defined as the maximal matching with maximum number of edges.
The number of edges in the maximum matching of ‘G’ is called its matching number.
Example
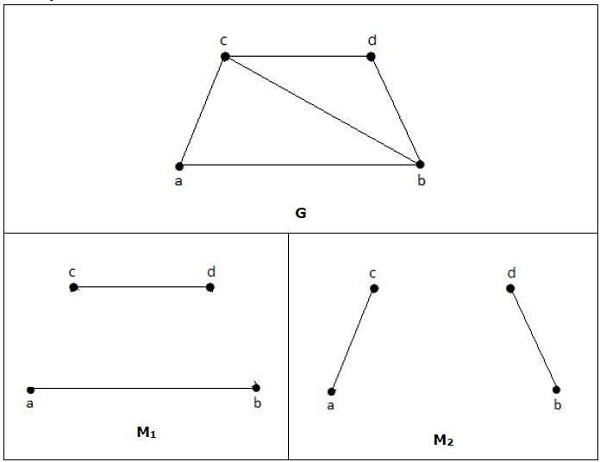
For a graph given in the above example, M1 and M2 are the maximum matching of ‘G’ and its matching number is 2. Hence by using the graph G, we can form only the subgraphs with only 2 edges maximum. Hence we have the matching number as two.
Perfect Matching
A matching (M) of graph (G) is said to be a perfect match, if every vertex of graph g (G) is incident to exactly one edge of the matching (M), i.e.,
deg(V) = 1 ∀ V
The degree of each and every vertex in the subgraph should have a degree of 1.
Example
In the following graphs, M1 and M2 are examples of perfect matching of G.
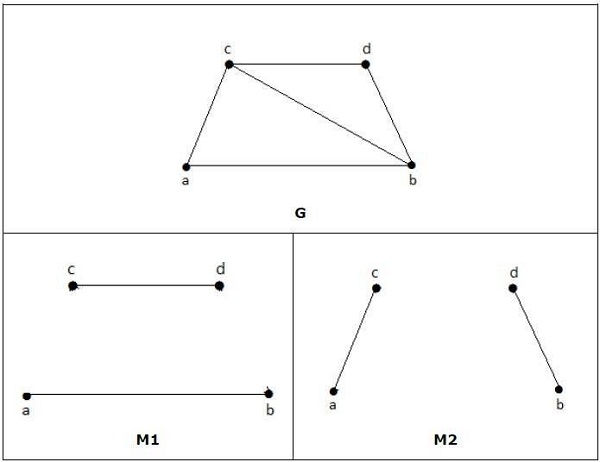
Note − Every perfect matching of graph is also a maximum matching of graph, because there is no chance of adding one more edge in a perfect matching graph.
A maximum matching of graph need not be perfect. If a graph ‘G’ has a perfect match, then the number of vertices |V(G)| is even. If it is odd, then the last vertex pairs with the other vertex, and finally there remains a single vertex which cannot be paired with any other vertex for which the degree is zero. It clearly violates the perfect matching principle.
Example
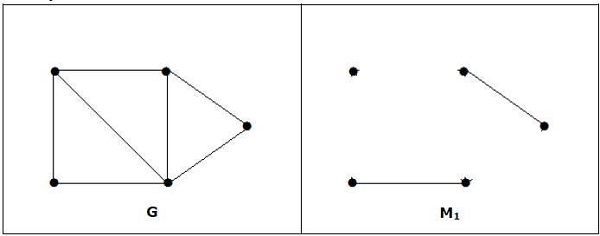
Note − The converse of the above statement need not be true. If G has even number of vertices, then M1 need not be perfect.
Example
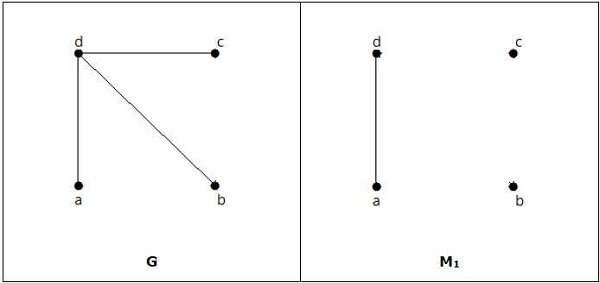
It is matching, but it is not a perfect match, even though it has even number of vertices.
Independent sets are represented in sets, in which
there should not be any edges adjacent to each other. There should not be any common vertex between any two edges.
there should not be any vertices adjacent to each other. There should not be any common edge between any two vertices.
Independent Line Set
Let ‘G’ = (V, E) be a graph. A subset L of E is called an independent line set of ‘G’ if no two edges in L are adjacent. Such a set is called an independent line set.
Example
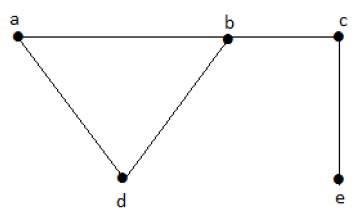
Let us consider the following subsets −
L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}In this example, the subsets L2 and L3 are clearly not the adjacent edges in the given graph. They are independent line sets. However L1 is not an independent line set, as for making an independent line set, there should be at least two edges.
Maximal Independent Line Set
An independent line set is said to be the maximal independent line set of a graph ‘G’ if no other edge of ‘G’ can be added to ‘L’.
Example
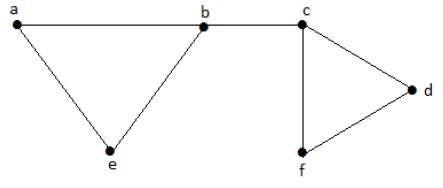
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L2 and L3 are maximal independent line sets/maximal matching. As for only these two subsets, there is no chance of adding any other edge which is not an adjacent. Hence these two subsets are considered as the maximal independent line sets.
Maximum Independent Line Set
A maximum independent line set of ‘G’ with maximum number of edges is called a maximum independent line set of ‘G’.
Number of edges in a maximum independent line set of G (β1)
= Line independent number of G
= Matching number of GExample
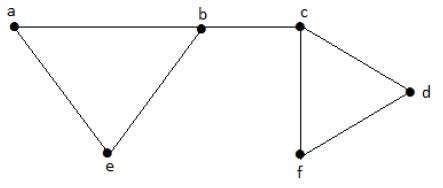
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L3 is the maximum independent line set of G with maximum edges which are not the adjacent edges in graph and is denoted by β1 = 3.
Note − For any graph G with no isolated vertex,
α1 + β1 = number of vertices in a graph = |V|
Example
Line covering number of Kn/Cn/wn,
$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:if\:n\:is\:even \\\frac{n+1}{2}\:if\:n\:is\:odd\end{cases}$$Line independent number (Matching number) = β1 = [n/2] α1 + β1 = n.
Independent Vertex Set
Let ‘G’ = (V, E) be a graph. A subset of ‘V’ is called an independent set of ‘G’ if no two vertices in ‘S’ are adjacent.
Example

Consider the following subsets from the above graphs −
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}Clearly S1 is not an independent vertex set, because for getting an independent vertex set, there should be at least two vertices in the from a graph. But here it is not that case. The subsets S2, S3, and S4 are the independent vertex sets because there is no vertex that is adjacent to any one vertex from the subsets.
Maximal Independent Vertex Set
Sia 'G' un grafo, allora un insieme di vertici indipendente di 'G' si dice che sia massimo se nessun altro vertice di 'G' può essere aggiunto a 'S'.
Example
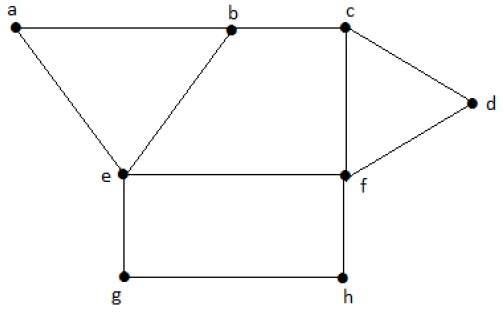
Considera i seguenti sottoinsiemi dai grafici sopra.
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}S 2 e S 3 sono i massimi insiemi di vertici indipendenti di "G". In S 1 e S 4 , possiamo aggiungere altri vertici; ma in S 2 e S 3 , non possiamo aggiungere nessun altro vertice.
Set massimo di vertici indipendenti
Un massimo insieme di vertici indipendenti di 'G' con il numero massimo di vertici è chiamato come il massimo insieme di vertici indipendenti.
Example

Considera i seguenti sottoinsiemi dal grafico sopra:
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}Solo S 3 è il massimo insieme di vertici indipendenti, poiché copre il numero più alto di vertici. Il numero di vertici in un massimo insieme di vertici indipendenti di 'G' è chiamato numero di vertici indipendenti di G (β 2 ).
Example
Per il grafico completo K n ,
Numero di copertura del vertice = α 2 = n − 1
Numero indipendente dal vertice = β 2 = 1
Hai α 2 + β 2 = n
In un grafo completo, ogni vertice è adiacente ai suoi rimanenti (n - 1) vertici. Pertanto, un insieme massimo indipendente di K n contiene solo un vertice.
Pertanto, β 2 = 1
e α 2 = | v | - β 2 = n-1
Note - Per qualsiasi grafico 'G' = (V, E)
- α 2 + β 2 = | v |
- Se 'S' è un insieme di vertici indipendente di 'G', allora (V - S) è una copertura di vertici di G.
La colorazione del grafico non è altro che un modo semplice per etichettare i componenti del grafico come vertici, bordi e regioni sotto alcuni vincoli. In un grafico, non ci sono due vertici adiacenti, bordi adiacenti o regioni adiacenti colorati con un numero minimo di colori. Questo numero è chiamatochromatic number e il grafico si chiama a properly colored graph.
Durante la colorazione del grafico, i vincoli impostati sul grafico sono i colori, l'ordine di colorazione, il modo di assegnare il colore, ecc. Viene data una colorazione a un vertice oa una particolare regione. Pertanto, i vertici o le regioni aventi gli stessi colori formano insiemi indipendenti.
Colorazione dei vertici
La colorazione dei vertici è un'assegnazione di colori ai vertici di un grafo 'G' in modo tale che non ci siano due vertici adiacenti dello stesso colore. In poche parole, non esistono due vertici di un bordo dello stesso colore.
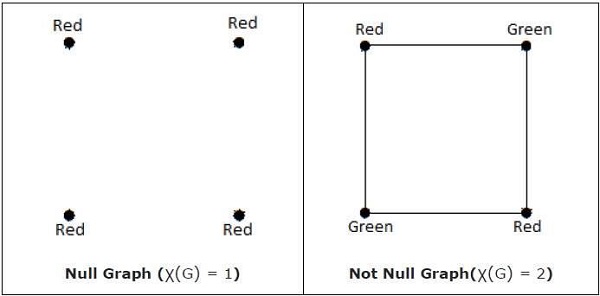
Numero cromatico
Il numero minimo di colori richiesto per la colorazione dei vertici del grafo "G" è chiamato come numero cromatico di G, indicato con X (G).
χ (G) = 1 se e solo se 'G' è un grafo nullo. Se 'G' non è un grafo nullo, allora χ (G) ≥ 2.
Example
Note - Un grafo 'G' si dice copribile con n se c'è una colorazione dei vertici che usa al massimo n colori, cioè X (G) ≤ n.
Colorazione della regione
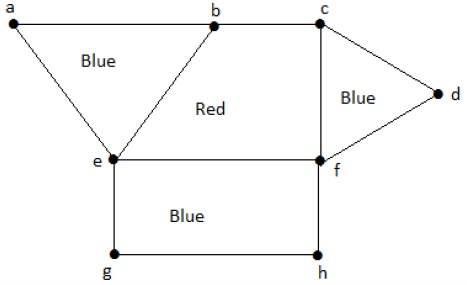
La colorazione della regione è un'assegnazione di colori alle regioni di un grafico planare in modo tale che non ci siano due regioni adiacenti dello stesso colore. Si dice che due regioni siano adiacenti se hanno un bordo comune.
Example
Dai un'occhiata al grafico seguente. Le regioni "aeb" e "befc" sono adiacenti, poiché esiste un confine comune "be" tra queste due regioni.
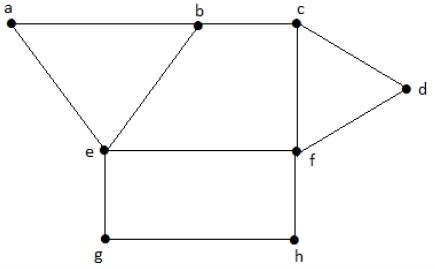
Allo stesso modo, anche le altre regioni sono colorate in base all'adiacenza. Questo grafico è colorato come segue:
Example
Il numero cromatico di Kn è
- n
- n–1
- [n/2]
- [n/2]
Considera questo esempio con K 4 .

Nel grafo completo, ogni vertice è adiacente ai rimanenti (n - 1) vertici. Quindi, ogni vertice richiede un nuovo colore. Da qui il numero cromatico di K n = n.
Applicazioni della colorazione dei grafici
La colorazione dei grafi è uno dei concetti più importanti nella teoria dei grafi. Viene utilizzato in molte applicazioni in tempo reale dell'informatica come:
- Clustering
- Estrazione dei dati
- Acquisizione di immagini
- Segmentazione delle immagini
- Networking
- Assegnazione delle risorse
- Pianificazione dei processi
Un grafo può esistere in forme diverse con lo stesso numero di vertici, bordi e anche la stessa connettività dei bordi. Tali grafici sono chiamati grafici isomorfi. Notare che etichettiamo i grafici in questo capitolo principalmente allo scopo di farvi riferimento e riconoscerli l'uno dall'altro.
Grafici isomorfi
Due grafici G 1 e G 2 si dicono isomorfi se -
Il loro numero di componenti (vertici e bordi) è lo stesso.
La loro connettività edge viene mantenuta.
Note- In breve, dei due grafici isomorfi, uno è una versione ottimizzata dell'altro. Un grafico senza etichetta può anche essere pensato come un grafico isomorfo.
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.Note
Se G 1 ≡ G 2 allora -
| V (Sol 1 ) | = | V (SOL 2 ) |
| E (G 1 ) | = | E (SOL 2 ) |
Le sequenze di gradi di G 1 e G 2 sono le stesse.
Se i vertici {V 1 , V 2 , .. Vk} formano un ciclo di lunghezza K in G 1 , allora i vertici {f (V 1 ), f (V 2 ),… f (Vk)} dovrebbero formare un ciclo di lunghezza K in G 2 .
Tutte le condizioni di cui sopra sono necessarie affinché i grafici G 1 e G 2 siano isomorfi, ma non sufficienti per dimostrare che i grafici sono isomorfi.
(G 1 ≡ G 2 ) se e solo se (G 1 - ≡ G 2 -) dove G 1 e G 2 sono grafici semplici.
(G 1 ≡ G 2 ) se le matrici di adiacenza di G 1 e G 2 sono uguali.
(G 1 ≡ G 2 ) se e solo se i corrispondenti sottografi di G 1 e G 2 (ottenuti cancellando alcuni vertici in G1 e le loro immagini nel grafo G 2 ) sono isomorfi.
Example
Quale dei seguenti grafici è isomorfo?
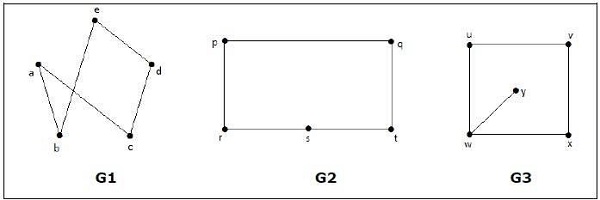
Nel grafo G 3 , il vertice "w" ha solo grado 3, mentre tutti gli altri vertici del grafo hanno grado 2. Quindi G3 non è isomorfo a G 1 o G 2 .
Prendendo i complementi di G 1 e G 2 , hai:
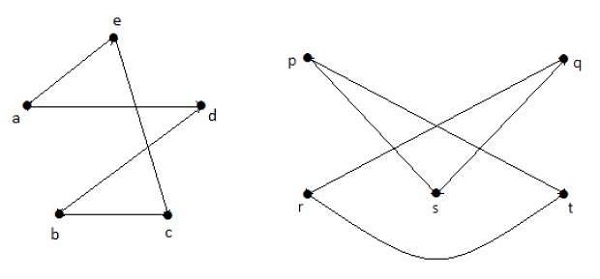
Qui, (G 1 - ≡ G 2 -), quindi (G 1 ≡ G 2 ).
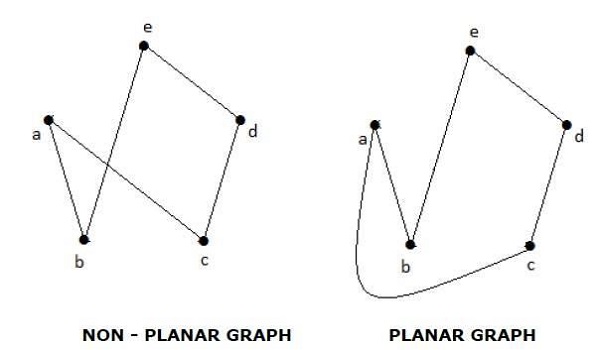
Grafici planari
Un grafico "G" si dice planare se può essere disegnato su un piano o una sfera in modo che non ci siano due bordi che si incrociano in un punto non vertice.
Example
Regioni
Ogni grafico planare divide il piano in aree collegate chiamate regioni.
Example
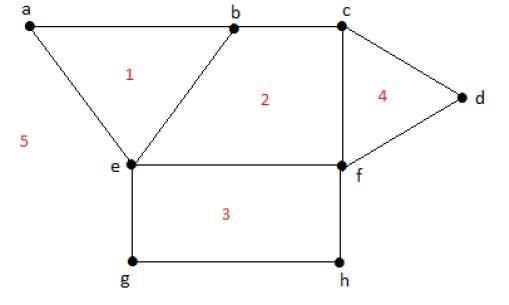
Grado di una regione delimitata r = deg(r) = Numero di bordi che racchiudono le regioni r.
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8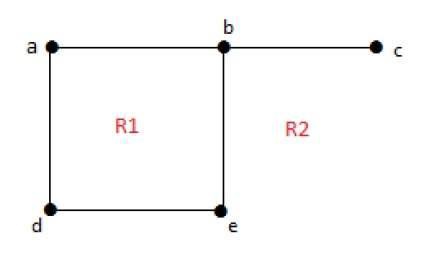
Grado di una regione illimitata r = deg(r) = Numero di bordi che racchiudono le regioni r.
deg(R1) = 4
deg(R2) = 6Nei grafici planari, le seguenti proprietà sono valide:
In un grafo planare con 'n' vertici, la somma dei gradi di tutti i vertici è -
Secondo Sum of Degrees of Regions/ Teorema, in un grafo planare con 'n' regioni, la somma dei gradi delle regioni è -
Sulla base del teorema di cui sopra, puoi trarre le seguenti conclusioni:
In un grafo planare,
Se il grado di ciascuna regione è K, la somma dei gradi delle regioni è -
Se il grado di ciascuna regione è almeno K (≥ K), allora
Se il grado di ciascuna regione è al massimo K (≤ K), allora
Note - Supponiamo che tutte le regioni abbiano lo stesso grado.
Secondo Euler’s Formulae su grafici planari,
Se un grafo 'G' è un planare connesso, allora
Se un grafico planare con componenti "K", allora
Dove, | V | è il numero di vertici, | E | è il numero di archi e | R | è il numero di regioni.
Disuguaglianza del vertice del bordo
Se 'G' è un grafo planare connesso con il grado di ciascuna regione almeno 'K', allora,
| E | ≤ k / (k-2) {| v | - 2}
Sai, | V | + | R | = | E | + 2
K. | R | ≤ 2 | E |
K (| E | - | V | + 2) ≤ 2 | E |
(K - 2) | E | ≤ K (| V | - 2)
| E | ≤ k / (k-2) {| v | - 2}
Se 'G' è un semplice grafo planare connesso, allora
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4Esiste almeno un vertice V • ∈ G, tale che deg (V) ≤ 5.
Se 'G' è un semplice grafo planare connesso (con almeno 2 bordi) e senza triangoli, allora
|E| ≤ {2|V| – 4}Teorema di Kuratowski
Un grafo "G" è non planare se e solo se "G" ha un sottografo omeomorfo a K 5 o K 3,3 .
Omomorfismo
Si dice che due grafi G 1 e G 2 siano omomorfi, se ciascuno di questi grafi può essere ottenuto dallo stesso grafo 'G' dividendo alcuni spigoli di G con più vertici. Dai un'occhiata al seguente esempio:

Dividi il bordo "rs" in due bordi aggiungendo un vertice.
I grafici mostrati di seguito sono omomorfi al primo grafico.
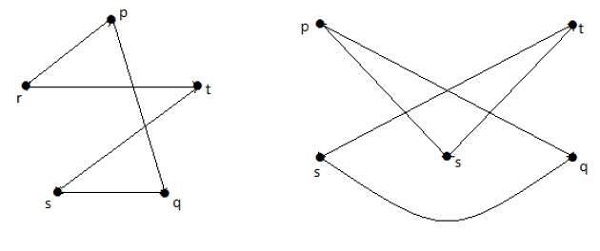
Se G 1 è isomorfo a G 2 , allora G è omeomorfo a G2 ma non è necessario che sia vero il contrario.
Qualsiasi grafo con 4 o meno vertici è planare.
Qualsiasi grafico con 8 o meno spigoli è planare.
Un grafo completo K n è planare se e solo se n ≤ 4.
Il grafo bipartito completo K m, n è planare se e solo se m ≤ 2 oppure n ≤ 2.
Un semplice grafo non planare con un numero minimo di vertici è il grafo completo K 5 .
Il grafo semplice non planare con un numero minimo di spigoli è K 3, 3 .
Grafico poliedrico
Un grafo planare connesso semplice è chiamato grafo poliedrico se il grado di ciascun vertice è ≥ 3, cioè deg (V) ≥ 3 ∀ V ∈ G.
3 | V | ≤ 2 | E |
3 | R | ≤ 2 | E |
Un grafo è attraversabile se è possibile disegnare un percorso tra tutti i vertici senza ripercorrere lo stesso percorso. Sulla base di questo percorso, ci sono alcune categorie come il percorso di Eulero e il circuito di Eulero che sono descritti in questo capitolo.
Sentiero di Eulero
Il percorso di Eulero contiene ogni lato di "G" esattamente una volta e ogni vertice di "G" almeno una volta. Si dice che un grafo connesso G sia attraversabile se contiene un percorso di Eulero.
Example
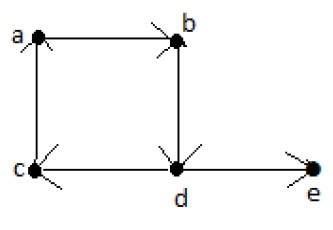
Sentiero di Eulero = dcabde.
Circuito di Eulero
Nel cammino di Eulero, se il vertice iniziale è uguale al vertice finale, allora è chiamato circuito di Eulero.
Example
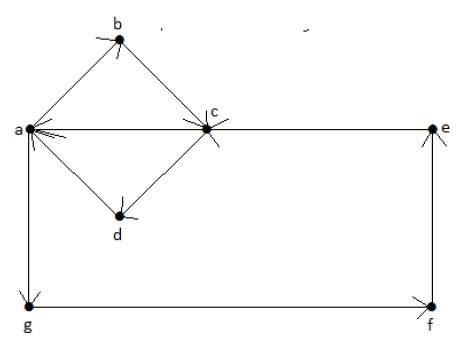
Euler’s Path = abcdagfeca.
Teorema del circuito di Eulero
Un grafo connesso 'G' è attraversabile se e solo se il numero di vertici con grado dispari in G è esattamente 2 o 0. Un grafo connesso G può contenere un percorso di Eulero, ma non un circuito di Eulero, se ha esattamente due vertici con un grado strano.
Note - Questo percorso di Eulero inizia con un vertice di grado dispari e termina con l'altro vertice di grado dispari.
Example
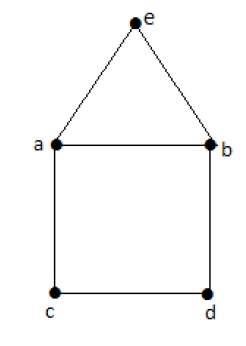
Euler’s Path- beabdca non è un circuito di Eulero, ma è un percorso di Eulero. Chiaramente ha esattamente 2 vertici di grado dispari.
Note - In un grafo connesso G, se il numero di vertici con grado dispari = 0, allora esiste il circuito di Eulero.
Grafico hamiltoniano
Si dice che un grafo connesso G sia un grafo hamiltoniano, se esiste un ciclo che contiene tutti i vertici di G.
Ogni ciclo è un circuito ma un circuito può contenere più cicli. Un tale ciclo è chiamato aHamiltonian cycle di G.
Sentiero Hamiltoniano
Un grafo connesso si dice hamiltoniano se contiene ogni vertice di G esattamente una volta. Tale percorso è chiamato aHamiltonian path.
Example
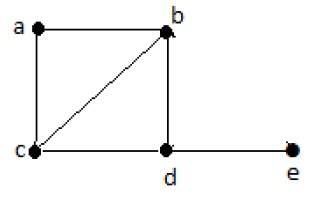
Hamiltonian Path- edbac.
Note
Il circuito di Eulero contiene ciascun bordo del grafico esattamente una volta.
In un ciclo hamiltoniano, alcuni bordi del grafico possono essere saltati.
Example
Dai un'occhiata al grafico seguente:
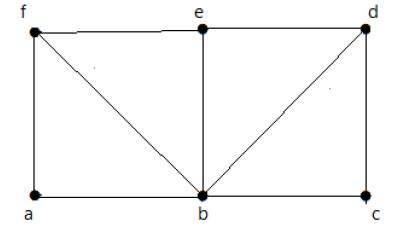
Per il grafico mostrato sopra -
Il sentiero di Eulero esiste - falso
Il circuito di Eulero esiste - falso
Il ciclo hamiltoniano esiste - vero
Il percorso hamiltoniano esiste - vero
G ha quattro vertici con grado dispari, quindi non è attraversabile. Saltando gli archi interni, il grafo ha un ciclo hamiltoniano passante per tutti i vertici.
In questo capitolo tratteremo alcuni esempi standard per dimostrare i concetti che abbiamo già discusso nei capitoli precedenti.
Esempio 1
Find the number of spanning trees in the following graph.
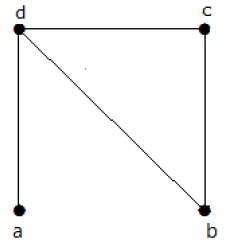
Soluzione
Il numero di spanning tree ottenuto dal grafico sopra è 3. Sono i seguenti:
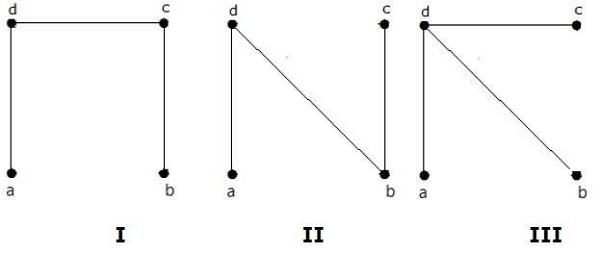
Questi tre sono gli spanning tree per i grafici dati. Qui i grafici I e II sono isomorfi tra loro. Chiaramente, il numero di spanning tree non isomorfi è due.
Esempio 2
How many simple non-isomorphic graphs are possible with 3 vertices?
Soluzione
Sono possibili 4 grafici non isomorfi con 3 vertici. Sono mostrati di seguito.
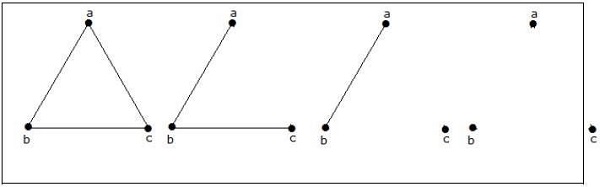
Esempio 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
Soluzione
Dalla somma dei gradi teorema,
20 Σ i = 1 deg (Vi) = 2 | E |
20 (3) = 2 | E |
| E | = 30
Secondo la formula di Eulero,
| V | + | R | = | E | + 2
20+ | R | = 30 + 2
| R | = 12
Quindi, il numero di regioni è 12.
Esempio 4
What is the chromatic number of complete graph Kn?
Soluzione
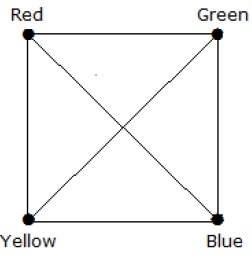
In un grafo completo, ogni vertice è adiacente ai rimanenti (n – 1) vertici. Quindi, ogni vertice richiede un nuovo colore. Da qui il numero cromatico K n = n.
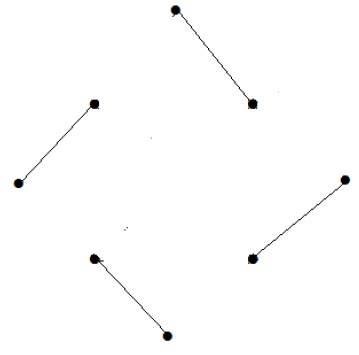
Esempio 5
What is the matching number for the following graph?
Soluzione
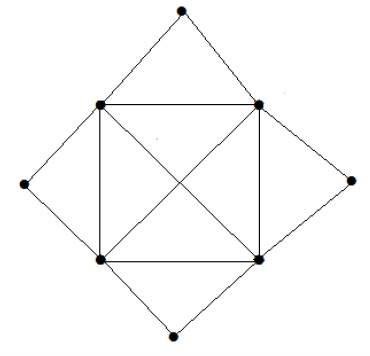
Numero di vertici = 9
Possiamo abbinare solo 8 vertici.
Il numero corrispondente è 4.
Esempio 6
What is the line covering number of for the following graph?
Soluzione
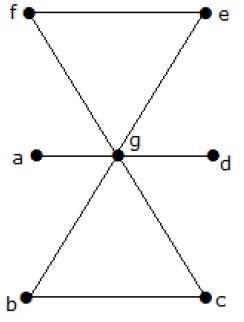
Numero di vertici = | V | = n = 7
Numero di copertura della linea = (α 1 ) ≥ [n / 2] = 3
α 1 ≥ 3
Usando 3 bordi, possiamo coprire tutti i vertici.
Quindi, il numero di copertura della linea è 3.