Teoria della rete - Guida rapida
Network theoryè lo studio per risolvere i problemi dei circuiti elettrici o delle reti elettriche. In questo capitolo introduttivo, discutiamo prima la terminologia di base dei circuiti elettrici e i tipi di elementi di rete.
Terminologia di base
In Network Theory, incontreremo spesso i seguenti termini:
- Circuito elettrico
- Rete elettrica
- Current
- Voltage
- Power
Quindi, è imperativo raccogliere alcune conoscenze di base su questi termini prima di procedere oltre. Cominciamo con Electric Circuit.
Circuito elettrico
Un circuito elettrico contiene un percorso chiuso per fornire un flusso di elettroni da una sorgente di tensione o una sorgente di corrente. Gli elementi presenti in un circuito elettrico saranno inseries connection, parallel connectiono in qualsiasi combinazione di collegamenti in serie e in parallelo.
Rete elettrica
Una rete elettrica non deve contenere un percorso chiuso per fornire un flusso di elettroni da una sorgente di tensione o una sorgente di corrente. Quindi, possiamo concludere che "tutti i circuiti elettrici sono reti elettriche", ma non è necessario che sia vero il contrario.
attuale
Il corrente "I"che scorre attraverso un conduttore non è altro che la velocità del flusso di carica. Matematicamente, può essere scritto come
$$I = \frac{dQ}{dt}$$
Dove,
Q è la carica e la sua unità è Coloumb.
t è il tempo e la sua unità è la seconda.
Per analogia, la corrente elettrica può essere considerata come il flusso dell'acqua attraverso un tubo. La corrente è misurata in termini diAmpere.
In generale, Electron current fluisce dal terminale negativo della sorgente al terminale positivo, mentre, Conventional current fluisce dal terminale positivo della sorgente al terminale negativo.
Electron current si ottiene grazie al movimento degli elettroni liberi, mentre, Conventional currentsi ottiene grazie alla circolazione di cariche positive gratuite. Entrambi sono chiamati comeelectric current.
Voltaggio
La tensione "V"non è altro che una forza elettromotrice che fa fluire la carica (elettroni). Matematicamente, può essere scritto come
$$V = \frac{dW}{dQ}$$
Dove,
W è l'energia potenziale e la sua unità è Joule.
Q è la carica e la sua unità è Coloumb.
Come analogia, la tensione può essere pensata come la pressione dell'acqua che fa fluire l'acqua attraverso un tubo. È misurato in termini diVolt.
Energia
Il potere "P"non è altro che la velocità del flusso di energia elettrica. Matematicamente, può essere scritto come
$$P = \frac{dW}{dt}$$
Dove,
W è l'energia elettrica e si misura in termini di Joule.
t è il tempo e si misura in secondi.
Possiamo riscrivere l'equazione precedente a
$$P = \frac{dW}{dt} = \frac{dW}{dQ} \times \frac{dQ}{dt} = VI$$
Perciò, power non è altro che il product di tensione V e attuale I. La sua unità èWatt.
Tipi di elementi di rete
Possiamo classificare gli elementi della Rete in varie tipologie in base ad alcuni parametri. Di seguito sono riportati i tipi di elementi di rete:
Elementi attivi ed elementi passivi
Elementi lineari ed elementi non lineari
Elementi bilaterali ed elementi unilaterali
Elementi attivi ed elementi passivi
Possiamo classificare gli elementi della rete in entrambi active o passive basato sulla capacità di fornire potere.
Active Elementsfornire potenza ad altri elementi, che sono presenti in un circuito elettrico. A volte, possono assorbire il potere come elementi passivi. Ciò significa che gli elementi attivi hanno la capacità di fornire e assorbire potenza.Examples: Fonti di tensione e sorgenti di corrente.
Passive Elementsnon possono fornire potenza (energia) ad altri elementi, tuttavia possono assorbire potenza. Ciò significa che questi elementi dissipano energia sotto forma di calore o immagazzinano energia sotto forma di campo magnetico o campo elettrico.Examples: Resistori, induttori e condensatori.
Elementi lineari ed elementi non lineari
Possiamo classificare gli elementi di rete come linear o non-linear in base alla loro caratteristica di obbedire alla proprietà della linearità.
Linear Elements sono gli elementi che mostrano una relazione lineare tra tensione e corrente. Examples: Resistori, induttori e condensatori.
Non-Linear Elements sono quelli che non mostrano una relazione lineare tra tensione e corrente. Examples: Fonti di tensione e sorgenti di corrente.
Elementi bilaterali ed elementi unilaterali
Gli elementi di rete possono anche essere classificati come entrambi bilateral o unilateral in base alla direzione dei flussi di corrente attraverso gli elementi della rete.
Bilateral Elements sono gli elementi che consentono la corrente in entrambe le direzioni e offrono la stessa impedenza in entrambe le direzioni del flusso di corrente. Examples: Resistori, induttori e condensatori.
Il concetto di elementi bilaterali è illustrato nelle figure seguenti.
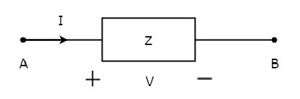
Nella figura sopra, la corrente (I) fluisce dai terminali A a B attraverso un elemento passivo avente impedenza Z Ω. È il rapporto della tensione (V) su quell'elemento tra i terminali A e B e la corrente (I).
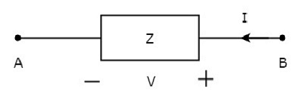
Nella figura sopra, la corrente (I) fluisce dai terminali B ad A attraverso un elemento passivo avente impedenza Z Ω. Ciò significa che la corrente (–I) fluisce dai terminali A verso B. Anche in questo caso si otterrà lo stesso valore di impedenza, poiché sia la corrente che la tensione hanno segno negativo rispetto ai terminali A e B.
Unilateral Elementssono quelli che permettono la corrente in una sola direzione. Quindi, offrono diverse impedenze in entrambe le direzioni.
Abbiamo discusso i tipi di elementi di rete nel capitolo precedente. Ora, identifichiamo il filenature of network elements dalle caratteristiche VI fornite negli esempi seguenti.
Esempio 1
Il V-I characteristics di un elemento di rete è mostrato di seguito.
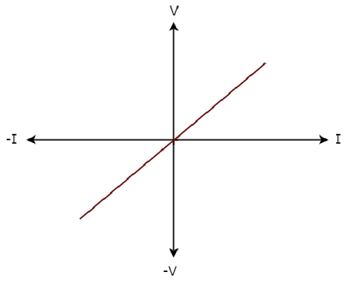
Step 1 - Verifica dell'elemento di rete come linear o non-linear.
Dalla figura sopra, le caratteristiche VI di un elemento di rete sono una linea retta passante per l'origine. Quindi, è un fileLinear element.
Step 2 - Verifica dell'elemento di rete come active o passive.
Le caratteristiche VI date di un elemento di rete si trovano nel primo e nel terzo quadrante.
Nel first quadrant, i valori di tensione (V) e corrente (I) sono positivi. Quindi, i rapporti di tensione (V) e corrente (I) danno valori di impedenza positivi.
Allo stesso modo, in third quadrant, i valori di tensione (V) e corrente (I) hanno valori negativi. Quindi, i rapporti di tensione (V) e corrente (I) producono valori di impedenza positivi.
Poiché le caratteristiche VI fornite offrono valori di impedenza positivi, l'elemento di rete è a Passive element.
Step 3 - Verifica dell'elemento di rete come bilateral o unilateral.
Per ogni punto (I, V) sulle caratteristiche, esiste un corrispondente punto (-I, -V) sulle caratteristiche date. Quindi, l'elemento di rete è un fileBilateral element.
Pertanto, le caratteristiche VI fornite mostrano che l'elemento di rete è un file Linear, Passive, e Bilateral element.
Esempio 2
Il V-I characteristics di un elemento di rete è mostrato di seguito.
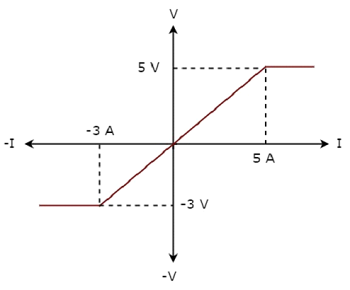
Step 1 - Verifica dell'elemento di rete come linear o non-linear.
Dalla figura sopra, le caratteristiche VI di un elemento di rete sono una linea retta solo tra i punti (-3A, -3V) e (5A, 5V). Al di là di questi punti, le caratteristiche del VI non seguono la relazione lineare. Quindi, è un fileNon-linear element.
Step 2 - Verifica dell'elemento di rete come active o passive.
Le caratteristiche VI date di un elemento di rete si trovano nel primo e nel terzo quadrante. In questi due quadranti, i rapporti di tensione (V) e corrente (I) producono valori di impedenza positivi. Quindi, l'elemento di rete è un filePassive element.
Step 3 - Verifica dell'elemento di rete come bilateral or unilateral.
Considera il punto (5A, 5V) sulle caratteristiche. Il punto corrispondente (-5A, -3V) esiste sulle caratteristiche date invece di (-5A, -5V). Quindi, l'elemento di rete è un fileUnilateral element.
Pertanto, le caratteristiche VI fornite mostrano che l'elemento di rete è un file Non-linear, Passive, e Unilateral element.
Active Elementssono gli elementi di rete che erogano potenza ad altri elementi presenti in un circuito elettrico. Quindi, gli elementi attivi sono anche chiamati come sorgenti di tensione o tipo di corrente. Possiamo classificare queste fonti nelle seguenti due categorie:
- Fonti indipendenti
- Fonti dipendenti
Fonti indipendenti
Come suggerisce il nome, sorgenti indipendenti producono valori fissi di tensione o corrente e questi non dipendono da nessun altro parametro. Le fonti indipendenti possono essere ulteriormente suddivise nelle seguenti due categorie:
- Fonti di tensione indipendenti
- Fonti correnti indipendenti
Fonti di tensione indipendenti
Una sorgente di tensione indipendente produce una tensione costante sui suoi due terminali. Questa tensione è indipendente dalla quantità di corrente che scorre attraverso i due terminali della sorgente di tensione.
Indipendente ideal voltage source e le sue caratteristiche VI sono mostrate nella figura seguente.
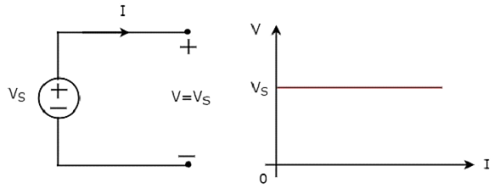
Il V-I characteristicsdi una sorgente di tensione ideale indipendente è una linea costante, che è sempre uguale alla tensione di sorgente (VS) indipendentemente dal valore di corrente (I). Quindi, la resistenza interna di una sorgente di tensione ideale indipendente è zero ohm.
Quindi, le sorgenti di tensione ideali indipendenti do not exist practically, perché ci sarà una certa resistenza interna.
Indipendente practical voltage source e le sue caratteristiche VI sono mostrate nella figura seguente.
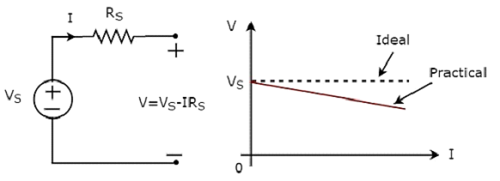
C'è una deviazione nelle caratteristiche VI di una sorgente di tensione pratica indipendente dalle caratteristiche VI di una sorgente di tensione ideale indipendente. Ciò è dovuto alla caduta di tensione attraverso la resistenza interna (R S ) di una sorgente di tensione pratica indipendente.
Fonti correnti indipendenti
Una sorgente di corrente indipendente produce una corrente costante. Questa corrente è indipendente dalla tensione ai suoi due terminali. Indipendenteideal current source e le sue caratteristiche VI sono mostrate nella figura seguente.

Il V-I characteristicsdi una sorgente di corrente ideale indipendente è una linea costante, che è sempre uguale alla corrente della sorgente (I S ) indipendentemente dal valore di tensione (V). Quindi, la resistenza interna di una sorgente di corrente ideale indipendente è infinita ohm.
Quindi, le sorgenti di corrente ideali indipendenti do not exist practically, perché ci sarà una certa resistenza interna.
Indipendente practical current source e le sue caratteristiche VI sono mostrate nella figura seguente.
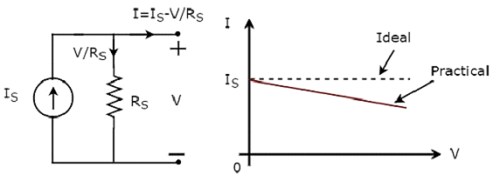
C'è una deviazione nelle caratteristiche VI di una sorgente di corrente pratica indipendente dalle caratteristiche VI di una sorgente di corrente ideale indipendente. Ciò è dovuto alla quantità di corrente che scorre attraverso la resistenza di shunt interna (R S ) di una sorgente di corrente pratica indipendente.
Fonti dipendenti
Come suggerisce il nome, le sorgenti dipendenti producono la quantità di tensione o corrente che dipende da un'altra tensione o corrente. Le fonti dipendenti sono anche chiamate comecontrolled sources. Le fonti dipendenti possono essere ulteriormente suddivise nelle seguenti due categorie:
- Fonti di tensione dipendenti
- Fonti correnti dipendenti
Fonti di tensione dipendenti
Una sorgente di tensione dipendente produce una tensione attraverso i suoi due terminali. La quantità di questa tensione dipende da qualche altra tensione o corrente. Quindi, le sorgenti di tensione dipendenti possono essere ulteriormente classificate nelle seguenti due categorie:
- Sorgente di tensione dipendente dalla tensione (VDVS)
- Fonte di tensione dipendente dalla corrente (CDVS)
Le sorgenti di tensione dipendenti sono rappresentate con i segni "+" e "-" all'interno di una forma a diamante. L'ampiezza della sorgente di tensione può essere rappresentata al di fuori della forma del diamante.
Fonti correnti dipendenti
Una sorgente di corrente dipendente produce una corrente. La quantità di questa corrente dipende da qualche altra tensione o corrente. Pertanto, le sorgenti di corrente dipendenti possono essere ulteriormente classificate nelle seguenti due categorie:
- Sorgente di corrente dipendente dalla tensione (VDCS)
- Current Dependent Current Source (CDCS)
Le sorgenti di corrente dipendenti sono rappresentate con una freccia all'interno di una forma di diamante. L'ampiezza della sorgente di corrente può essere rappresentata al di fuori della forma del diamante.
Possiamo osservare queste sorgenti dipendenti o controllate in modelli equivalenti di transistor.
Tecnica di trasformazione della sorgente
Sappiamo che ci sono due fonti pratiche, vale a dire, voltage source e current source. Possiamo trasformare (convertire) una sorgente nell'altra in base al requisito, risolvendo i problemi di rete.
La tecnica per trasformare una fonte nell'altra è chiamata come source transformation technique. Di seguito sono riportate le due possibili trasformazioni della sorgente:
- Pratica sorgente di tensione in una pratica sorgente di corrente
- Pratica sorgente di corrente in una pratica sorgente di tensione
Pratica sorgente di tensione in una pratica sorgente di corrente
La trasformazione della pratica sorgente di tensione in una pratica sorgente di corrente è mostrata nella figura seguente
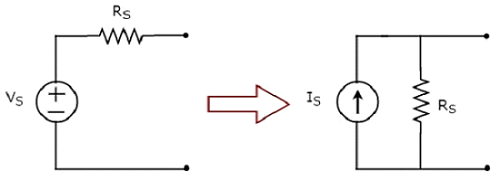
Practical voltage sourceè costituito da una sorgente di tensione (V S ) in serie con una resistenza (R S ). Questo può essere convertito in una pratica sorgente di corrente come mostrato in figura. Consiste in una sorgente di corrente (I S ) in parallelo con un resistore (R S ).
Il valore di IS sarà uguale al rapporto tra V S ed R S . Matematicamente, può essere rappresentato come
$$I_S = \frac{V_S}{R_S}$$
Pratica sorgente di corrente in una pratica sorgente di tensione
La trasformazione della pratica sorgente di corrente in una pratica sorgente di tensione è mostrata nella figura seguente.
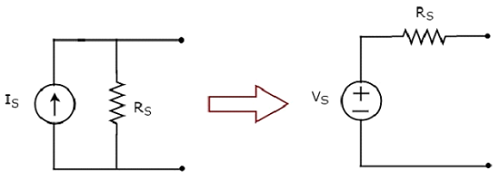
La pratica sorgente di corrente è costituita da una sorgente di corrente (I S ) in parallelo con un resistore (R S ). Questo può essere convertito in una pratica sorgente di tensione come mostrato in figura. Consiste in una sorgente di tensione (V S ) in serie con un resistore (R S ).
Il valore di V S sarà uguale al prodotto di I S e R S . Matematicamente, può essere rappresentato come
$$V_S = I_S R_S$$
In questo capitolo, discuteremo in dettaglio degli elementi passivi come resistore, induttore e condensatore. Cominciamo con le resistenze.
Resistore
La funzionalità principale del resistore è opporsi o limitare il flusso di corrente elettrica. Quindi, i resistori vengono utilizzati per limitare la quantità di flusso di corrente e / o la tensione di divisione (condivisione).
Lascia che la corrente che scorre attraverso il resistore sia I ampere e la tensione ai suoi capi sia V volt. Ilsymbol di resistenza insieme a corrente, I e tensione, V sono mostrati nella figura seguente.
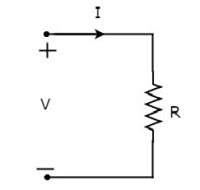
Secondo Ohm’s law, la tensione attraverso il resistore è il prodotto della corrente che scorre attraverso di esso e la resistenza di quel resistore. Mathematically, può essere rappresentato come
$V = IR$ Equation 1
$\Rightarrow I = \frac{V}{R}$Equation 2
Dove, R è la resistenza di un resistore.
Dall'equazione 2, possiamo concludere che la corrente che scorre attraverso il resistore è direttamente proporzionale alla tensione applicata attraverso il resistore e inversamente proporzionale alla resistenza del resistore.
Power in un circuito elettrico l'elemento può essere rappresentato come
$P = VI$Equation 3
Sostituisci, equazione 1 nell'equazione 3.
$P = (IR)I$
$\Rightarrow P = I^2 R$ Equation 4
Sostituisci, equazione 2 nell'equazione 3.
$P = V \lgroup \frac{V}{R} \rgroup$
$\Rightarrow P = \frac{V^2}{R}$ Equation 5
Quindi, possiamo calcolare la quantità di potenza dissipata nel resistore utilizzando una delle formule menzionate nelle equazioni da 3 a 5.
Induttore
In generale, gli induttori avranno un numero di giri. Quindi, producono un flusso magnetico quando la corrente scorre attraverso di esso. Quindi, la quantità di flusso magnetico totale prodotto da un induttore dipende dalla corrente, lo attraverso e hanno una relazione lineare.
Mathematically, può essere scritto come
$$\Psi \: \alpha \: I$$
$$\Rightarrow \Psi = LI$$
Dove,
Ψ è il flusso magnetico totale
L è l'induttanza di un induttore
Lascia che la corrente che scorre attraverso l'induttore sia I ampere e la tensione ai suoi capi sia V volt. Ilsymboldell'induttore insieme alla corrente I e alla tensione V sono mostrati nella figura seguente.
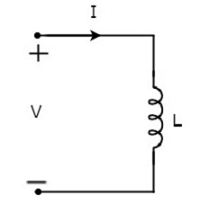
Secondo Faraday’s law, la tensione ai capi dell'induttore può essere scritta come
$$V = \frac{d\Psi}{dt}$$
Sostituisci Ψ = LI nell'equazione precedente.
$$V = \frac{d(LI)}{dt}$$
$$\Rightarrow V = L \frac{dI}{dt}$$
$$\Rightarrow I = \frac{1}{L} \int V dt$$
Dalle equazioni precedenti, possiamo concludere che esiste a linear relationship tra la tensione attraverso l'induttore e la corrente che lo attraversa.
Lo sappiamo power in un circuito elettrico l'elemento può essere rappresentato come
$$P = VI$$
Sostituto $V = L \frac{dI}{dt}$ nell'equazione precedente.
$$P = \lgroup L \frac{dI}{dt}\rgroup I$$
$$\Rightarrow P = LI \frac{dI}{dt}$$
Integrando l'equazione di cui sopra, otterremo il energy memorizzato in un induttore come
$$W = \frac{1}{2} LI^2$$
Quindi, l'induttore immagazzina l'energia sotto forma di campo magnetico.
Condensatore
In generale, un condensatore ha due piastre conduttive, separate da un mezzo dielettrico. Se viene applicata una tensione positiva attraverso il condensatore, memorizza la carica positiva. Allo stesso modo, se viene applicata una tensione negativa attraverso il condensatore, memorizza la carica negativa.
Quindi, la quantità di carica immagazzinata nel condensatore dipende dalla tensione applicata Vattraverso di essa e hanno una relazione lineare. Matematicamente, può essere scritto come
$$Q \: \alpha \: V$$
$$\Rightarrow Q = CV$$
Dove,
Q è la carica immagazzinata nel condensatore.
C è la capacità di un condensatore.
Lascia che la corrente che scorre attraverso il condensatore sia I ampere e la tensione ai suoi capi sia V volt. Il simbolo del condensatore insieme alla corrente I e alla tensione V sono mostrati nella figura seguente.
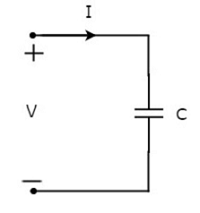
Sappiamo che il file current non è altro che il time rate of flow of charge. Matematicamente, può essere rappresentato come
$$I = \frac{dQ}{dt}$$
Sostituto $Q = CV$ nell'equazione precedente.
$$I = \frac{d(CV)}{dt}$$
$$\Rightarrow I = C \frac{dV}{dt}$$
$$\Rightarrow V = \frac{1}{C} \int I dt$$
Dalle equazioni precedenti, possiamo concludere che esiste a linear relationship tra la tensione attraverso il condensatore e la corrente che lo attraversa.
Lo sappiamo power in un circuito elettrico l'elemento può essere rappresentato come
$$P = VI$$
Sostituto $I = C \frac{dV}{dt}$ nell'equazione precedente.
$$P = V \lgroup C \frac{dV}{dt} \rgroup$$
$$\Rightarrow P = CV \frac{dV}{dt}$$
Integrando l'equazione di cui sopra, otterremo il energy memorizzato nel condensatore come
$$W = \frac{1}{2}CV^2$$
Quindi, il condensatore immagazzina l'energia sotto forma di campo elettrico.
Gli elementi di rete possono essere uno dei due active o passivegenere. Qualsiasi circuito o rete elettrica contiene uno di questi due tipi di elementi di rete o una combinazione di entrambi.
Ora, discutiamo delle seguenti due leggi, comunemente note come Kirchhoff’s laws.
- Legge attuale di Kirchhoff
- Legge di Kirchhoff sulla tensione
Legge attuale di Kirchhoff
La legge corrente di Kirchhoff (KCL) afferma che la somma algebrica delle correnti che escono (o entrano) da un nodo è uguale a zero.
UN Nodeè un punto in cui due o più elementi del circuito sono collegati ad esso. Se solo due elementi del circuito sono collegati a un nodo, si dice che sia un nodo semplice. Se tre o più elementi del circuito sono collegati a un nodo, si dice che lo siaPrincipal Node.
Mathematically, KCL può essere rappresentato come
$$\displaystyle\sum\limits_{m=1}^M I_m = 0$$
Dove,
Imè la m esima corrente di ramo che lascia il nodo.
M è il numero di rami collegati a un nodo.
La dichiarazione di cui sopra di KCLpuò anche essere espresso come "la somma algebrica delle correnti che entrano in un nodo è uguale alla somma algebrica delle correnti che escono da un nodo". Cerchiamo di verificare questa affermazione attraverso il seguente esempio.
Esempio
Scrivi KCL equation al nodo P della figura seguente.
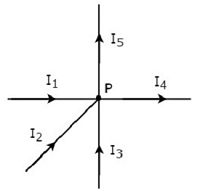
Nella figura sopra, le correnti di derivazione I 1 , I 2 e I 3 sonoentering al nodo P. Quindi, considera i segni negativi per queste tre correnti.
Nella figura sopra, le correnti di derivazione I 4 e I 5 sonoleaving dal nodo P. Quindi, considera i segni positivi per queste due correnti.
Il KCL equation al nodo P sarà
$$- I_1 - I_2 - I_3 + I_4 + I_5 = 0$$
$$\Rightarrow I_1 + I_2 + I_3 = I_4 + I_5$$
Nell'equazione precedente, il lato sinistro rappresenta la somma delle correnti in entrata, mentre il lato destro rappresenta la somma delle correnti in uscita.
In questo tutorial, considereremo il segno positivo quando la corrente lascia un nodo e il segno negativo quando entra in un nodo. Allo stesso modo, puoi considerare il segno negativo quando la corrente lascia un nodo e il segno positivo quando entra in un nodo. In entrambi i casi, ilresult will be same.
Note - KCL è indipendente dalla natura degli elementi di rete collegati a un nodo.
Legge di Kirchhoff sulla tensione
La legge della tensione di Kirchhoff (KVL) afferma che la somma algebrica delle tensioni attorno a un anello o una maglia è uguale a zero.
UN Loopè un percorso che termina nello stesso nodo da cui è partito. Al contrario, aMesh è un loop che non contiene altri loop al suo interno.
Matematicamente, KVL può essere rappresentato come
$$\displaystyle\sum\limits_{n=1}^N V_n = 0$$
Dove,
Vnè la tensione dell'elemento n- esimo in un loop (mesh).
N è il numero di elementi di rete nel loop (mesh).
La dichiarazione di cui sopra di KVLpuò anche essere espresso come "la somma algebrica delle sorgenti di tensione è uguale alla somma algebrica delle cadute di tensione presenti in un loop". Verifichiamo questa affermazione con l'aiuto del seguente esempio.
Esempio
Scrivi KVL equation intorno al ciclo del circuito seguente.
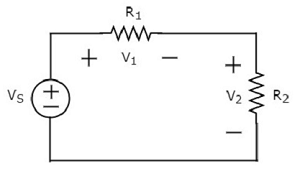
Lo schema circuitale sopra è costituito da una sorgente di tensione, V S in serie con due resistori R 1 e R 2 . Le cadute di tensione sui resistori R 1 e R 2 sono rispettivamente V 1 e V 2 .
Applicare KVL intorno al ciclo.
$$V_S - V_1 - V_2 = 0$$
$$\Rightarrow V_S = V_1 + V_2$$
Nell'equazione precedente, il termine a sinistra rappresenta la singola sorgente di tensione VS. Considerando che, il lato destro rappresenta ilsum of voltage drops. In questo esempio, abbiamo considerato solo una sorgente di tensione. Ecco perché il lato sinistro contiene un solo termine. Se consideriamo più sorgenti di tensione, il lato sinistro contiene la somma delle sorgenti di tensione.
In questo tutorial, consideriamo il segno della tensione di ogni elemento come la polarità del secondo terminale che è presente mentre si viaggia intorno al loop. Allo stesso modo, puoi considerare il segno di ogni tensione come la polarità del primo terminale che è presente mentre viaggi intorno al loop. In entrambi i casi, ilresult will be same.
Note - KVL è indipendente dalla natura degli elementi di rete presenti in un loop.
In questo capitolo, discutiamo i seguenti due principi di divisione delle grandezze elettriche.
- Principio di divisione attuale
- Principio della divisione della tensione
Principio di divisione attuale
Quando due o più elementi passivi sono collegati in parallelo, la quantità di corrente che scorre attraverso ogni elemento ottiene divided (condivisi) tra di loro dalla corrente che sta entrando nel nodo.
Considera quanto segue circuit diagram.
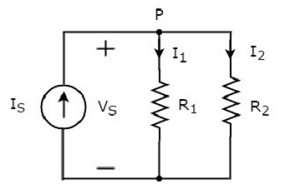
Lo schema circuitale sopra è costituito da una sorgente di corrente in ingresso IS in parallelo con due resistenze R1 e R2. La tensione su ogni elemento èVS. Le correnti che fluiscono attraverso le resistenzeR1 e R2 siamo I1 e I2 rispettivamente.
Il KCL equation al nodo P sarà
$$I_S = I_1 + I_2$$
Sostituto $I_1 = \frac{V_S}{R_1}$ e $I_2 = \frac{V_S}{R_2}$ nell'equazione precedente.
$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} = V_S \lgroup \frac {R_2 + R_1 }{R_1 R_2} \rgroup$$
$$\Rightarrow V_S = I_S \lgroup \frac{R_1R_2}{R_1 + R_2} \rgroup$$
Sostituisci il valore di V S in$I_1 = \frac{V_S}{R_1}$.
$$I_1 = \frac{I_S}{R_1}\lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$
$$\Rightarrow I_1 = I_S\lgroup \frac{R_2}{R_1 + R_2} \rgroup$$
Sostituisci il valore di V S in$I_2 = \frac{V_S}{R_2}$.
$$I_2 = \frac{I_S}{R_2} \lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$
$$\Rightarrow I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$
Dalle equazioni di I 1 e I 2 , possiamo generalizzare che la corrente che scorre attraverso qualsiasi elemento passivo può essere trovata usando la seguente formula.
$$I_N = I_S \lgroup \frac{Z_1\rVert Z_2 \rVert...\rVert Z_{N-1}}{Z_1 + Z_2 + ... + Z_N}\rgroup$$
Questo è noto come current division principle ed è applicabile, quando due o più elementi passivi sono collegati in parallelo e solo una corrente entra nel nodo.
Dove,
I N è la corrente che scorre attraverso l'elemento passivo del ramo N- esimo .
I S è la corrente di ingresso, che entra nel nodo.
Z 1 , Z 2 , ..., Z N sono le impedenze di 1 ° ramo, 2 ° ramo, ..., N ° ramo rispettivamente.
Principio della divisione della tensione
Quando due o più elementi passivi sono collegati in serie, la quantità di tensione presente su ogni elemento ottiene divided (condivisi) tra di loro dal voltaggio disponibile attraverso l'intera combinazione.
Considera quanto segue circuit diagram.
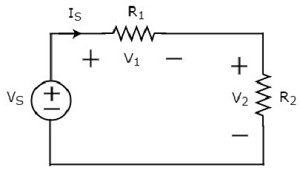
Lo schema circuitale sopra è costituito da una sorgente di tensione, V S in serie con due resistori R 1 e R 2 . La corrente che fluisce attraverso questi elementi è che S . Le cadute di tensione sui resistori R 1 e R 2 sono rispettivamente V 1 e V 2 .
Il KVL equation intorno al ciclo sarà
$$V_S = V_1 + V_2$$
Sostituisci V 1 = I S R 1 e V 2 = I S R 2 nell'equazione precedente
$$V_S = I_S R_1 + I_S R_2 = I_S(R_1 + R_2)$$
$$I_S = \frac{V_S}{R_1 + R_2}$$
Sostituisci il valore di I S in V 1 = I S R 1 .
$$V_1 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_1$$
$$\Rightarrow V_1 = V_S \lgroup \frac {R_1}{R_1 + R_2} \rgroup$$
Sostituisci il valore di I S in V 2 = I S R 2 .
$$V_2 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_2$$
$$\Rightarrow V_2 = V_S \lgroup \frac {R_2}{R_1 + R_2} \rgroup$$
Dalle equazioni di V 1 e V 2 , possiamo generalizzare che la tensione attraverso qualsiasi elemento passivo può essere trovata usando la seguente formula.
$$V_N = V_S \lgroup \frac {Z_N}{Z_1 + Z_2 +....+ Z_N}\rgroup$$
Questo è noto come voltage division principle ed è applicabile quando due o più elementi passivi sono collegati in serie e una sola tensione è disponibile sull'intera combinazione.
Dove,
V N è la tensione attraverso N- esimo elemento passivo.
V S è la tensione di ingresso, che è presente nell'intera combinazione di elementi passivi in serie.
Z 1 , Z 2 , ..., Z 3 sono le impedenze di 1 ° elemento passivo, 2 ° elemento passivo, ..., N ° elemento passivo, rispettivamente.
Esistono due metodi di base utilizzati per risolvere qualsiasi rete elettrica: Nodal analysis e Mesh analysis. In questo capitolo, parliamo diNodal analysis metodo.
Nell'analisi nodale, considereremo le tensioni di nodo rispetto a Ground. Quindi, l'analisi nodale è anche chiamata comeNode-voltage method.
Procedura di analisi nodale
Seguire questi passaggi durante la risoluzione di qualsiasi rete o circuito elettrico utilizzando l'analisi nodale.
Step 1 - Identifica il file principal nodes e scegli uno di loro come reference node. Tratteremo quel nodo di riferimento come Ground.
Step 2 - Etichetta il file node voltages rispetto a Ground da tutti i nodi principali tranne il nodo di riferimento.
Step 3 - Scrivi nodal equationsa tutti i nodi principali tranne il nodo di riferimento. L'equazione nodale si ottiene applicando prima KCL e poi la legge di Ohm.
Step 4 - Risolvi le equazioni nodali ottenute nel passaggio 3 per ottenere le tensioni dei nodi.
Ora, possiamo trovare la corrente che scorre attraverso qualsiasi elemento e la tensione attraverso qualsiasi elemento presente nella rete data utilizzando le tensioni dei nodi.
Esempio
Trova la corrente che scorre attraverso la resistenza da 20 Ω del seguente circuito usando Nodal analysis.
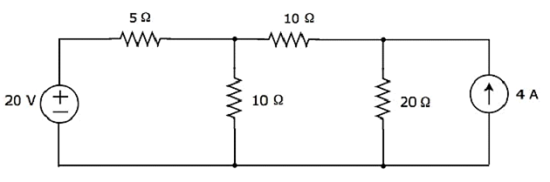
Step 1 - Ci sono three principle nodesnel circuito sopra. Questi sono etichettati come 1, 2 e 3 nella figura seguente.
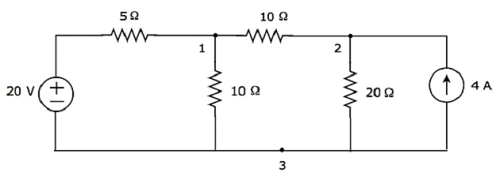
Nella figura sopra, considera node 3 come nodo di riferimento (Ground).
Step 2- Le tensioni dei nodi, V 1 e V 2 , sono indicate nella figura seguente.
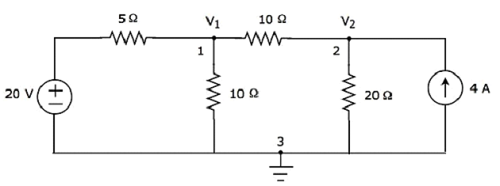
Nella figura sopra, V 1 è la tensione dal nodo 1 rispetto a massa e V 2 è la tensione dal nodo 2 rispetto a massa.
Step 3 - In questo caso, otterremo two nodal equations, poiché ci sono due nodi principali, 1 e 2, diversi da Ground. Quando scriviamo le equazioni nodali in un nodo, assumiamo che tutte le correnti stiano partendo dal nodo per il quale la direzione della corrente non è menzionata e la tensione di quel nodo sia maggiore delle altre tensioni di nodo nel circuito.
Il nodal equation al nodo 1 è
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1 - V_2}{10} = 0$$
$$\Rightarrow \frac{2 V_1 - 40 + V_1 + V_1 - V_2}{10} = 0$$
$$\Rightarrow 4V_1 - 40 - V_2 = 0$$
$\Rightarrow V_2 = 4V_1 - 40$ Equation 1
Il nodal equation al nodo 2 è
$$-4 + \frac{V_2}{20} + \frac{V_2 - V_1}{10} = 0$$
$$\Rightarrow \frac{-80 + V_2 + 2V_2 - 2V_2}{20} = 0$$
$\Rightarrow 3V_2 − 2V_1 = 80$ Equation 2
Step 4- Trovare le tensioni dei nodi, V 1 e V 2 risolvendo l'Equazione 1 e l'Equazione 2.
Sostituisci l'equazione 1 nell'equazione 2.
$$3(4 V_1 - 40) - 2 V_1 = 80$$
$$\Rightarrow 12 V_1 - 120 - 2V_1 =80$$
$$\Rightarrow 10 V_1 = 200$$
$$\Rightarrow V_1 = 20V$$
Sostituisci V 1 = 20 V nell'equazione 1.
$$V_2 = 4(20) - 40$$
$$\Rightarrow V_2 = 40V$$
Quindi, abbiamo ottenuto le tensioni di nodo V 1 e V 2 come20 V e 40 V rispettivamente.
Step 5- La tensione sul resistore da 20 Ω non è altro che la tensione del nodo V 2 ed è uguale a 40 V. Ora, possiamo trovare la corrente che scorre attraverso il resistore da 20 Ω usando la legge di Ohm.
$$I_{20 \Omega} = \frac{V_2}{R}$$
Sostituisci i valori di V 2 e R nell'equazione precedente.
$$I_{20 \Omega} = \frac{40}{20}$$
$$\Rightarrow I_{20 \Omega} = 2A$$
Pertanto, la corrente che scorre attraverso il resistore da 20 Ω di un dato circuito è 2 A.
Note- Dall'esempio sopra, possiamo concludere che dobbiamo risolvere 'n' equazioni nodali, se il circuito elettrico ha 'n' nodi principali (eccetto il nodo di riferimento). Pertanto, possiamo scegliere l'analisi nodale quando ilnumber of principal nodes (tranne il nodo di riferimento) è inferiore al numero di maglie di qualsiasi circuito elettrico.
Nell'analisi Mesh, considereremo le correnti che fluiscono attraverso ciascuna mesh. Quindi, l'analisi della mesh è anche chiamata comeMesh-current method.
UN branchè un percorso che unisce due nodi e contiene un elemento di circuito. Se un ramo appartiene a una sola maglia, la corrente del ramo sarà uguale alla corrente della maglia.
Se un ramo è comune a due maglie, la corrente del ramo sarà uguale alla somma (o differenza) di due correnti di maglia, quando sono nella stessa (o opposta) direzione.
Procedura di analisi della mesh
Segui questi passaggi durante la risoluzione di qualsiasi rete o circuito elettrico utilizzando l'analisi Mesh.
Step 1 - Identifica il file meshes ed etichettare le correnti di maglia in senso orario o antiorario.
Step 2 - Osservare la quantità di corrente che scorre attraverso ogni elemento in termini di correnti di maglia.
Step 3 - Scrivi mesh equationsa tutte le maglie. L'equazione della mesh si ottiene applicando prima KVL e poi la legge di Ohm.
Step 4 - Risolvi le equazioni della mesh ottenute nel passaggio 3 per ottenere il file mesh currents.
Ora, possiamo trovare la corrente che scorre attraverso qualsiasi elemento e la tensione attraverso qualsiasi elemento presente nella rete data utilizzando correnti di maglia.
Esempio
Trova la tensione attraverso il resistore da 30 Ω usando Mesh analysis.
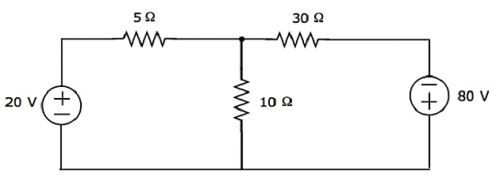
Step 1- Ci sono due maglie nel circuito sopra. Ilmesh currentsI 1 e I 2 sono considerati in senso orario. Queste correnti di maglia sono mostrate nella figura seguente.
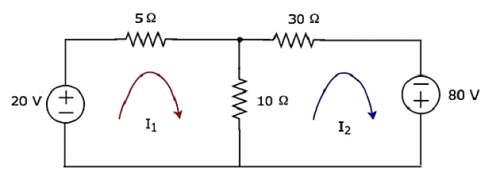
Step 2- La corrente di maglia I 1 scorre attraverso una sorgente di tensione da 20 V e una resistenza da 5 Ω. Allo stesso modo, la corrente di maglia I 2 scorre attraverso un resistore da 30 Ω e una sorgente di tensione di -80 V. Ma la differenza di due correnti di maglia, I 1 e I 2 , scorre attraverso un resistore da 10 Ω, poiché è il ramo comune di due maglie.
Step 3 - In questo caso, otterremo two mesh equationspoiché ci sono due maglie nel circuito dato. Quando scriviamo le equazioni di mesh, assumiamo che la corrente di mesh di quella particolare mesh sia maggiore di tutte le altre correnti di mesh del circuito.
Il mesh equation della prima maglia è
$$20 - 5I_1 -10(I_1 - I_2) = 0$$
$$\Rightarrow 20 - 15I_1 + 10I_2 = 0$$
$$\Rightarrow 10I_2 = 15I_1 - 20$$
Dividi l'equazione precedente per 5.
$$2I_2 = 3I_1 - 4$$
Moltiplica l'equazione precedente per 2.
$4I_2 = 6I_1 - 8$ Equation 1
Il mesh equation della seconda maglia è
$$-10(I_2 - I_1) - 30I_2 + 80 = 0$$
Dividi l'equazione precedente per 10.
$$-(I_2 - I_1) - 3I_2 + 8 = 0$$
$$\Rightarrow -4I_2 + I_1 + 8 = 0$$
$4I_2 = I_1 + 8$ Equation 2
Step 4- Trovare le correnti di maglia I 1 e I 2 risolvendo l'Equazione 1 e l'Equazione 2.
I termini a sinistra dell'equazione 1 e dell'equazione 2 sono gli stessi. Quindi, equipara i termini a destra dell'equazione 1 e dell'equazione 2 per trovare il valore di I 1 .
$$6I_1 - 8 = I_1 + 8$$
$$\Rightarrow 5I_1 = 16$$
$$\Rightarrow I_1 = \frac{16}{5} A$$
Sostituisci il valore I 1 nell'equazione 2.
$$4I_2 = \frac{16}{5} + 8$$
$$\Rightarrow 4I_2 = \frac{56}{5}$$
$$\Rightarrow I_2 = \frac{14}{5} A$$
Quindi, abbiamo le correnti di maglia I 1 e I 2 come$\mathbf{\frac{16}{5}}$ A e $\mathbf{\frac{14}{5}}$ A rispettivamente.
Step 5- La corrente che scorre attraverso la resistenza da 30 Ω non è altro che la corrente di maglia I 2 ed è uguale a$\frac{14}{5}$ R. Ora, possiamo trovare la tensione su un resistore da 30 Ω usando la legge di Ohm.
$$V_{30 \Omega} = I_2 R$$
Sostituisci i valori di I 2 e R nell'equazione precedente.
$$V_{30 \Omega} = \lgroup \frac{14}{5} \rgroup 30$$
$$\Rightarrow V_{30 \Omega} = 84V$$
Pertanto, la tensione attraverso il resistore da 30 Ω del circuito dato è 84 V.
Note 1- Dall'esempio sopra, possiamo concludere che dobbiamo risolvere equazioni di maglia "m", se il circuito elettrico ha maglie "m". Ecco perché possiamo scegliere Analisi mesh quando il numero di mesh è inferiore al numero di nodi principali (eccetto il nodo di riferimento) di qualsiasi circuito elettrico.
Note 2 - Possiamo scegliere Analisi Nodale o Analisi Mesh, quando il numero di mesh è uguale al numero di nodi principali (eccetto il nodo di riferimento) in un qualsiasi circuito elettrico.
Se un circuito è costituito da due o più elementi passivi simili e sono collegati esclusivamente in serie o in parallelo, allora possiamo sostituirli con un unico elemento passivo equivalente. Quindi, questo circuito è chiamato come fileequivalent circuit.
In questo capitolo, discutiamo dei seguenti due circuiti equivalenti.
- Circuito equivalente in serie
- Circuito equivalente parallelo
Circuito equivalente in serie
Se elementi passivi simili sono collegati in series, quindi la stessa corrente scorrerà attraverso tutti questi elementi. Ma la tensione viene divisa tra ogni elemento.
Considera quanto segue circuit diagram.
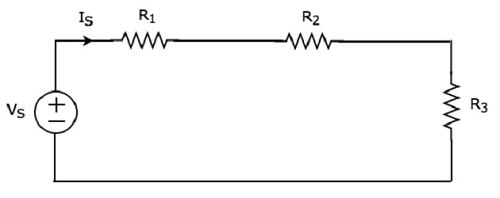
Ha un'unica sorgente di tensione (V S ) e tre resistori con resistenze R 1 , R 2 e R 3 . Tutti questi elementi sono collegati in serie. L'attuale IS scorre attraverso tutti questi elementi.
Il circuito sopra ha una sola mesh. IlKVL equation intorno a questa maglia c'è
$$V_S = V_1 + V_2 + V_3$$
Sostituto $V_1 = I_S R_1, \: V_2 = I_S R_2$ e $V_3 = I_S R_3$ nell'equazione precedente.
$$V_S = I_S R_1 + I_S R_2 + I_S R_3$$
$$\Rightarrow V_S = I_S(R_1 + R_2 + R_3)$$
L'equazione di cui sopra ha la forma di $V_S = I_S R_{Eq}$ dove,
$$R_{Eq} = R_1 + R_2 + R_3$$
Il equivalent circuit diagram del circuito dato è mostrato nella figura seguente.
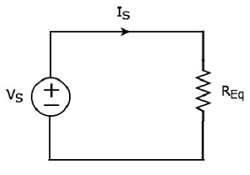
Ciò significa che se più resistori sono collegati in serie, è possibile sostituirli con un equivalent resistor. La resistenza di questo resistore equivalente è uguale alla somma delle resistenze di tutti quei resistori multipli.
Note 1- Se 'N' induttori con induttanze di L 1 , L 2 , ..., L N sono collegati in serie, allora ilequivalent inductance sarà
$$L_{Eq} = L_1 + L_2 + ... + L_N$$
Note 2- Se sono collegati in serie condensatori 'N' con capacità C 1 , C 2 , ..., C N , ilequivalent capacitance sarà
$$\frac{1}{C_{Eq}} = \frac{1}{C_1} + \frac{1}{C_2} + ... + \frac{1}{C_N}$$
Circuito equivalente parallelo
Se elementi passivi simili sono collegati in parallel, quindi la stessa tensione verrà mantenuta su ogni elemento. Ma la corrente che scorre attraverso ogni elemento viene divisa.
Considera quanto segue circuit diagram.

Ha un'unica sorgente di corrente (I S ) e tre resistori con resistenze R 1 , R 2 e R 3 . Tutti questi elementi sono collegati in parallelo. La tensione (V S ) è disponibile su tutti questi elementi.
Il circuito sopra ha un solo nodo principale (P) eccetto il nodo di massa. IlKCL equation a questo nodo principale (P) è
$$I_S = I_1 + I_2 + I_3$$
Sostituto $I_1 = \frac{V_S}{R_1}, \: I_2 = \frac{V_S}{R_2}$ e $I_3 = \frac{V_S}{R_3}$ nell'equazione precedente.
$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} + \frac{V_S}{R_3}$$
$$\Rightarrow I_S = V_S \lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup$$
$$\Rightarrow V_S = I_S\left [ \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup} \right ]$$
L'equazione di cui sopra è nella forma di V S = I S R Eq dove,
$$R_{Eq} = \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup}$$
$$\frac{1}{R_{Eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$
The equivalent circuit diagram of the given circuit is shown in the following figure.
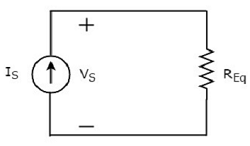
That means, if multiple resistors are connected in parallel, then we can replace them with an equivalent resistor. The resistance of this equivalent resistor is equal to the reciprocal of sum of reciprocal of each resistance of all those multiple resistors.
Note 1 − If ‘N’ inductors having inductances of L1, L2, ..., LN are connected in parallel, then the equivalent inductance will be
$$\frac{1}{L_{Eq}} = \frac{1}{L_1} + \frac{1}{L_2} + ... + \frac{1}{L_N}$$
Note 2 − If ‘N’ capacitors having capacitances of C1, C2, ..., CN are connected in parallel, then the equivalent capacitance will be
$$C_{Eq} = C_1 + C_2 + ... + C_N$$
In the previous chapter, we discussed about the equivalent circuits of series combination and parallel combination individually. In this chapter, let us solve an example problem by considering both series and parallel combinations of similar passive elements.
Example
Let us find the equivalent resistance across the terminals A & B of the following electrical network.

We will get the equivalent resistance across terminals A & B by minimizing the above network into a single resistor between those two terminals. For this, we have to identify the combination of resistors that are connected in series form and parallel form and then find the equivalent resistance of the respective form in every step.
The given electrical network is modified into the following form as shown in the following figure.
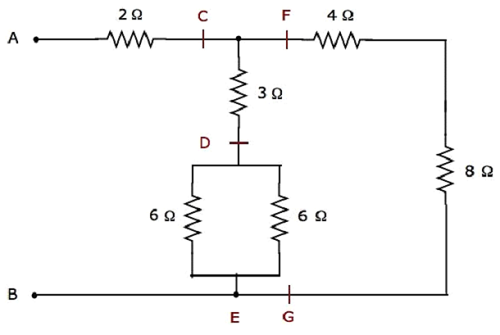
In the above figure, the letters, C to G, are used for labelling various terminals.
Step 1 − In the above network, two 6 Ω resistors are connected in parallel. So, the equivalent resistance between D & E will be 3 Ω. This can be obtained by doing the following simplification.
$$R_{DE} = \frac{6 \times 6}{6 + 6} = \frac{36}{12} = 3 \Omega$$
In the above network, the resistors 4 Ω and 8 Ω are connected in series. So, the equivalent resistance between F & G will be 12 Ω. This can be obtained by doing the following simplification.
$$R_{FG} = 4 + 8 = 12 \Omega$$
Step 2 − The simplified electrical network after Step 1 is shown in the following figure.
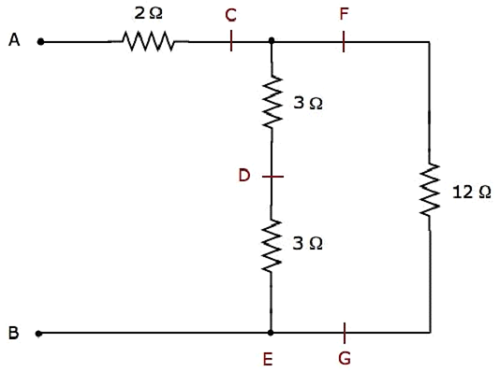
In the above network, two 3 Ω resistors are connected in series. So, the equivalent resistance between C & E will be 6 Ω. This can be obtained by doing the following simplification.
$$R_{CE} = 3 + 3 = 6 \Omega$$
Step 3 − The simplified electrical network after Step 2 is shown in the following figure.

In the above network, the resistors 6 Ω and 12 Ω are connected in parallel. So, the equivalent resistance between C & B will be 4 Ω. This can be obtained by doing the following simplification.
$$R_{CB} = \frac{6 \times 12}{6 + 12} = \frac{72}{18} = 4 \Omega$$
Step 4 − The simplified electrical network after Step 3 is shown in the following figure.
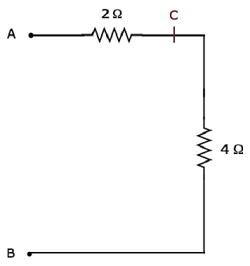
In the above network, the resistors 2 Ω and 4 Ω are connected in series between the terminals A & B. So, the equivalent resistance between A & B will be 6 Ω. This can be obtained by doing the following simplification.
$$R_{AB} = 2 + 4 = 6 \Omega$$
Therefore, the equivalent resistance between terminals A & B of the given electrical network is 6 Ω.
In the previous chapter, we discussed an example problem related equivalent resistance. There, we calculated the equivalent resistance between the terminals A & B of the given electrical network easily. Because, in every step, we got the combination of resistors that are connected in either series form or parallel form.
However, in some situations, it is difficult to simplify the network by following the previous approach. For example, the resistors connected in either delta (δ) form or star form. In such situations, we have to convert the network of one form to the other in order to simplify it further by using series combination or parallel combination. In this chapter, let us discuss about the Delta to Star Conversion.
Delta Network
Consider the following delta network as shown in the following figure.
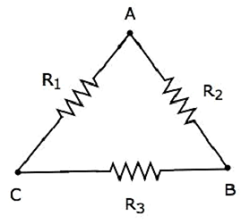
The following equations represent the equivalent resistance between two terminals of delta network, when the third terminal is kept open.
$$R_{AB} = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$$
$$R_{BC} = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$$
$$R_{CA} = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$$
Star Network
La figura seguente mostra il file equivalent star network corrispondente alla rete delta di cui sopra.
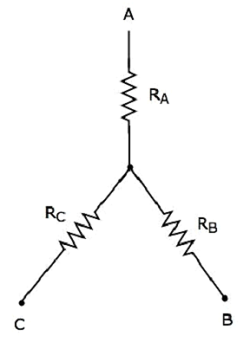
Le seguenti equazioni rappresentano il equivalent resistance tra due terminali della rete a stella, quando il terzo terminale è tenuto aperto.
$$R_{AB} = R_A + R_B$$
$$R_{BC} = R_B + R_C$$
$$R_{CA} = R_C + R_A$$
Resistenze della rete a stella in termini di resistenze della rete delta
Otterremo le seguenti equazioni equiparando i termini del lato destro delle equazioni precedenti per le quali i termini del lato sinistro sono gli stessi.
$R_A + R_B = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$ Equation 1
$R_B + R_C = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$ Equation 2
$R_C + R_A = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$ Equation 3
Aggiungendo le tre equazioni precedenti, otterremo
$$2(R_A + R_B + R_C) = \frac{2(R_1 R_2 + R_2 R_3 + R_3 R_1)}{R_1 + R_2 + R_3}$$
$\Rightarrow R_A + R_B + R_C = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3}$ Equation 4
Sottrai l'equazione 2 dall'equazione 4.
$R_A + R_B + R_C - (R_B + R_C) = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3} - \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$
$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$
Sottraendo l'equazione 3 dall'equazione 4, otterremo
$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$
Sottraendo l'equazione 1 dall'equazione 4, otterremo
$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$
Utilizzando le relazioni di cui sopra, possiamo trovare le resistenze della rete a stella dalle resistenze della rete delta. In questo modo, possiamo convertire un filedelta network in un star network.
Esempio
Calcoliamo il resistances of star network, che sono equivalenti a quella della rete delta come mostrato nella figura seguente.
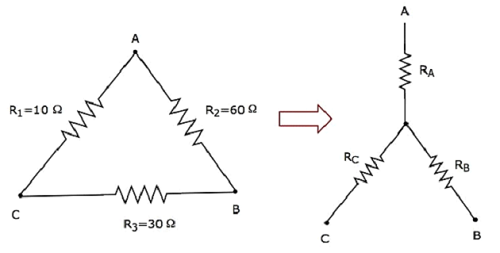
dato che resistances of delta networkcome R 1 = 10 Ω, R 2 = 60 Ω e R 3 = 30 Ω.
Conosciamo le seguenti relazioni delle resistenze della rete a stella in termini di resistenze della rete delta.
$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$
$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$
$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$
Sostituisci i valori di R 1 , R 2 e R 3 nelle equazioni precedenti.
$$R_A = \frac{10 \times 60}{10 +60+30} = \frac{600}{100} = 6\Omega$$
$$R_B = \frac{60 \times 30}{10 +60+30} = \frac{1800}{100} = 18\Omega$$
$$R_C = \frac{30 \times 10}{10 +60+30} = \frac{300}{100} = 3\Omega$$
Quindi, abbiamo le resistenze della rete stellare come RA = 6 Ω, RB = 18 Ω e RC = 3 Ω, che sono equivalenti alle resistenze della rete delta data.
Nel capitolo precedente, abbiamo discusso della conversione della rete delta in una rete a stella equivalente. Ora, parliamo della conversione della rete a stella in una rete delta equivalente. Questa conversione è chiamata comeStar to Delta Conversion.
Nel capitolo precedente, abbiamo ottenuto il file resistances of star network dalla rete delta come
$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ Equation 1
$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ Equation 2
$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ Equation 3
Resistenze della rete Delta in termini di resistenze della rete a stella
Manipoliamo le equazioni precedenti per ottenere le resistenze della rete delta in termini di resistenze della rete a stella.
Multiply ogni insieme di due equazioni e poi add.
$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$
$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$
$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ Equation 4
Dividendo l'equazione 4 per l'equazione 2, otterremo
$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$
$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
Dividendo l'equazione 4 per l'equazione 3, otterremo
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
Dividendo l'equazione 4 per l'equazione 1, otterremo
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
Utilizzando le relazioni di cui sopra, possiamo trovare le resistenze della rete delta dalle resistenze della rete a stella. In questo modo possiamo convertircistar network into delta network.
Esempio
Calcoliamo il resistances of delta network, che sono equivalenti a quella della rete a stella come mostrato nella figura seguente.
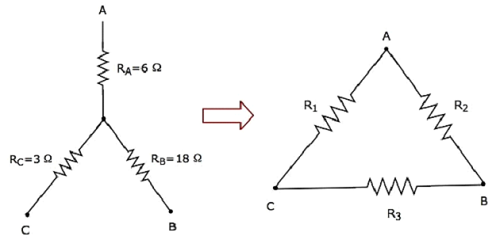
dato che resistances of star networkcome R A = 6 Ω, R B = 18 Ω e R C = 3 Ω .
Conosciamo le seguenti relazioni di resistances of delta network in termini di resistenze della rete a stella.
$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
Sostituisci i valori di R A , R B e R C nelle equazioni precedenti.
$$R_1 = 3 + 6 + \frac{3 \times 6}{18} = 9 + 1 = 10 \Omega$$
$$R_2 = 6 + 18 + \frac{6 \times 18}{3} = 24 + 36 = 60 \Omega$$
$$R_3 = 18 + 3 + \frac{18 \times 3}{6} = 21 + 9 = 30 \Omega$$
Quindi, abbiamo le resistenze della rete delta come R1 = 10 Ω, R2 = 60 Ω e R3 = 30 Ω, che sono equivalenti alle resistenze della rete a stella data.
La topologia di rete è una rappresentazione grafica dei circuiti elettrici. È utile per analizzare circuiti elettrici complessi convertendoli in grafici di rete. La topologia di rete è anche chiamataGraph theory.
Terminologia di base della topologia di rete
Ora, parliamo della terminologia di base coinvolta in questa topologia di rete.
Grafico
Il grafo di rete è chiamato semplicemente come graph. Consiste in un insieme di nodi collegati da rami. Nei grafici, un nodo è un punto comune di due o più rami. A volte, solo un singolo ramo può connettersi al nodo. Un ramo è un segmento di linea che collega due nodi.
Qualsiasi circuito elettrico o rete può essere convertito nel suo equivalente graphsostituendo gli elementi passivi e le sorgenti di tensione con cortocircuiti e le sorgenti di corrente con circuiti aperti. Ciò significa che i segmenti di linea nel grafico rappresentano i rami corrispondenti agli elementi passivi o alle sorgenti di tensione del circuito elettrico.
Esempio
Consideriamo quanto segue electric circuit.
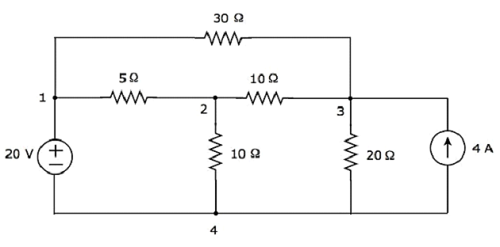
Nel circuito sopra, ci sono four principal nodes e quelli sono etichettati con 1, 2, 3 e 4. Ci sono seven branches nel circuito sopra, tra cui un ramo contiene una sorgente di tensione a 20 V, un altro ramo contiene una sorgente di corrente da 4 A e i restanti cinque rami contengono resistenze con resistenze rispettivamente di 30 Ω, 5 Ω, 10 Ω, 10 Ω e 20 Ω.
Un equivalente graph corrispondente al circuito elettrico di cui sopra è mostrato nella figura seguente.
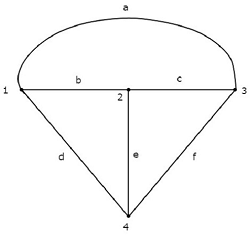
Nel grafico sopra, ci sono four nodese quelli sono etichettati rispettivamente con 1, 2, 3 e 4. Questi sono gli stessi dei nodi principali del circuito elettrico. Ci sonosix branches nel grafico sopra e quelli sono etichettati con a, b, c, d, e & f rispettivamente.
In questo caso, abbiamo one branch less nel grafico perché la sorgente di corrente da 4 A è realizzata come circuito aperto, convertendo il circuito elettrico nel suo grafico equivalente.
Da questo esempio, possiamo concludere i seguenti punti:
Il number of nodes presente in un grafo sarà uguale al numero di nodi principali presenti in un circuito elettrico.
Il number of branches presente in un grafico sarà minore o uguale al numero di rami presenti in un circuito elettrico.
Tipi di grafici
Di seguito sono riportati i tipi di grafici:
- Grafico connesso
- Grafico non connesso
- Grafico diretto
- Grafico non diretto
Ora, discutiamo questi grafici uno per uno.
Grafico connesso
Se esiste almeno un ramo tra uno qualsiasi dei due nodi di un grafo, viene chiamato come file connected graph. Ciò significa che ogni nodo nel grafo connesso avrà uno o più rami ad esso collegati. Quindi, nessun nodo si presenterà come isolato o separato.
Il grafico mostrato nell'esempio precedente è un connected graph. Qui, tutti i nodi sono collegati da tre rami.
Grafico non connesso
Se esiste almeno un nodo nel grafo che rimane scollegato anche da un singolo ramo, viene chiamato come file unconnected graph. Quindi, ci saranno uno o più nodi isolati in un grafo non connesso.
Considera il grafico mostrato nella figura seguente.
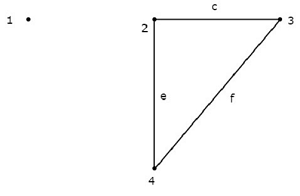
In questo grafico, i nodi 2, 3 e 4 sono collegati da due rami ciascuno. Ma nemmeno un singolo ramo è stato collegato alnode 1. Quindi, il nodo 1 diventa un fileisolated node. Quindi, il grafico sopra è un fileunconnected graph.
Grafico diretto
Se tutti i rami di un grafico sono rappresentati con frecce, quel grafico viene chiamato come un file directed graph. Queste frecce indicano la direzione del flusso di corrente in ogni ramo. Quindi, questo grafico è anche chiamato comeoriented graph.
Considera il grafico mostrato nella figura seguente.
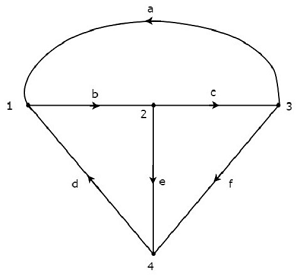
Nel grafico sopra, la direzione del flusso di corrente è rappresentata con una freccia in ogni ramo. Quindi, è un filedirected graph.
Grafico non diretto
Se i rami di un grafico non sono rappresentati con frecce, il grafico viene chiamato come file undirected graph. Poiché non ci sono direzioni del flusso di corrente, questo grafico è anche chiamato come fileunoriented graph.
Il grafico che è stato mostrato nel primo esempio di questo capitolo è un file unoriented graph, perché non ci sono frecce sui rami di quel grafico.
Sottografo e suoi tipi
Una parte del grafico è chiamata come file subgraph. Otteniamo sottografi rimuovendo alcuni nodi e / o rami di un dato grafo. Quindi, il numero di rami e / o nodi di un sottografo sarà inferiore a quello del grafico originale. Quindi, possiamo concludere che un sottografo è un sottoinsieme di un grafico.
Di seguito sono riportati i file two types di sottografi.
- Tree
- Co-Tree
Albero
L'albero è un sottografo connesso di un dato grafo, che contiene tutti i nodi di un grafo. Ma non dovrebbe esserci alcun loop in quel sottografo. I rami di un albero sono chiamati cometwigs.
Considera quanto segue connected subgraph del grafico, che è mostrato nell'esempio all'inizio di questo capitolo.
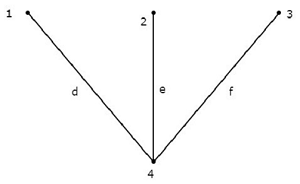
Questo sottografo connesso contiene tutti i quattro nodi del grafo dato e non c'è loop. Quindi, è un fileTree.
Questo albero ha solo tre rami su sei rami di un dato grafico. Perché, se consideriamo anche un singolo ramo dei restanti rami del grafico, ci sarà un ciclo nel sottografo connesso sopra. Quindi, il sottografo connesso risultante non sarà un albero.
Dall'albero sopra, possiamo concludere che il file number of branches che sono presenti in un albero dovrebbero essere uguali a n - 1 dove 'n' è il numero di nodi del grafo dato.
Co-Tree
Co-Tree è un sottografo, che si forma con i rami che vengono rimossi durante la formazione di un albero. Quindi, è chiamato comeComplementdi un albero. Per ogni albero, ci sarà un Co-albero corrispondente ei suoi rami saranno chiamati comelinkso accordi. In generale, i collegamenti sono rappresentati con linee tratteggiate.
Il Co-Tree corrispondente all'albero di cui sopra è mostrato nella figura seguente.
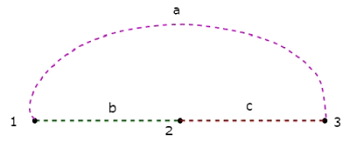
Questo Co-Tree ha solo tre nodi invece di quattro nodi del grafico dato, perché il Nodo 4 è isolato dal Co-Tree sopra. Pertanto, il Co-Tree non deve essere un sottografo connesso. Questo Co-Tree ha tre rami e formano un anello.
Il number of branchesche sono presenti in un co-albero saranno uguali alla differenza tra il numero di rami di un dato grafo e il numero di ramoscelli. Matematicamente, può essere scritto come
$$l = b - (n - 1)$$
$$l = b - n + 1$$
Dove,
- l è il numero di collegamenti.
- b è il numero di rami presenti in un dato grafico.
- n è il numero di nodi presenti in un dato grafo.
Se combiniamo un albero e il suo corrispondente Co-albero, otterremo il original graph come mostrato di seguito.
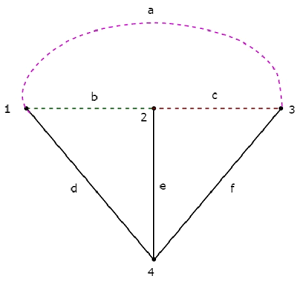
I rami dell'albero d, e & f sono rappresentati con linee continue. I rami del co-albero a, b e c sono rappresentati con linee tratteggiate.
Nel capitolo precedente, abbiamo discusso come convertire un circuito elettrico in un grafico equivalente. Ora, parliamo delle matrici della topologia di rete che sono utili per risolvere qualsiasi circuito elettrico o problema di rete utilizzando i loro grafici equivalenti.
Matrici associate a grafici di rete
Di seguito sono riportate le tre matrici utilizzate nella teoria dei grafi.
- Matrice di incidenza
- Matrice del ciclo fondamentale
- Matrice del set di taglio fondamentale
Matrice di incidenza
Una matrice di incidenza rappresenta il grafico di un dato circuito o rete elettrica. Quindi, è possibile disegnare il grafico di quello stesso circuito o rete elettrica dalincidence matrix.
Sappiamo che il grafico è costituito da un insieme di nodi e questi sono collegati da alcuni rami. Quindi, il collegamento di rami a un nodo è chiamato come incidenza. La matrice di incidenza è rappresentata con la lettera A. Viene anche chiamata matrice di incidenza da nodo a ramo onode incidence matrix.
Se sono presenti "n" nodi e rami "b" sono presenti in a directed graph, quindi la matrice di incidenza avrà "n" righe e "b" colonne. Qui, righe e colonne corrispondono ai nodi e ai rami di un grafo diretto. Quindi ilorder della matrice di incidenza sarà n × b.
Il elements of incidence matrix avrà uno di questi tre valori, +1, -1 e 0.
Se la corrente del ramo esce da un nodo selezionato, il valore dell'elemento sarà +1.
Se la corrente del ramo sta entrando verso un nodo selezionato, il valore dell'elemento sarà -1.
Se la corrente del ramo non entra in un nodo selezionato né esce da un nodo selezionato, il valore dell'elemento sarà 0.
Procedura per trovare la matrice di incidenza
Seguire questi passaggi per trovare la matrice di incidenza del grafico diretto.
Seleziona un nodo alla volta del dato grafico diretto e inserisci i valori degli elementi della matrice di incidenza corrispondenti a quel nodo in una riga.
Ripetere il passaggio precedente per tutti i nodi del dato grafico diretto.
Esempio
Considera quanto segue directed graph.

Il incidence matrix corrispondente al grafico sopra indicato sarà
$$A = \begin{bmatrix}-1 & 1 & 0 & -1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \\0 & 0 & 0 & 1 & -1 & -1 \end{bmatrix}$$
Le righe e le colonne della matrice di cui sopra rappresentano i nodi e i rami di un dato grafo diretto. L'ordine di questa matrice di incidenza è 4 × 6.
Osservando la matrice di incidenza di cui sopra, possiamo concludere che il summationdegli elementi di colonna della matrice di incidenza è uguale a zero. Ciò significa che una corrente di ramo parte da un nodo ed entra solo in un altro nodo singolo.
Note- Se il grafico dato è di tipo non diretto, convertilo in un grafico diretto rappresentando le frecce su ogni suo ramo. Possiamo considerare la direzione arbitraria del flusso di corrente in ogni ramo.
Matrice del ciclo fondamentale
Ciclo fondamentale o f-loopè un ciclo, che contiene solo un collegamento e uno o più ramoscelli. Quindi, il numero di f-loop sarà uguale al numero di collegamenti. La matrice del ciclo fondamentale è rappresentata con la lettera B. È anche chiamata comefundamental circuit matrixe matrice tie-set. Questa matrice fornisce la relazione tra le correnti di ramo e le correnti di collegamento.
Se sono presenti "n" nodi e rami "b" sono presenti in a directed graph, quindi il numero di collegamenti presenti in un co-albero, che corrisponde all'albero selezionato di un dato grafo, sarà b-n + 1.
Quindi, la matrice del ciclo fondamentale avrà righe "b-n + 1" e colonne "b". Qui, righe e colonne corrispondono ai collegamenti del co-albero e dei rami di un dato grafico. Quindi, l'ordine della matrice del ciclo fondamentale sarà(b - n + 1) × b.
Il elements of fundamental loop matrix avrà uno di questi tre valori, +1, -1 e 0.
Il valore dell'elemento sarà +1 per il collegamento dell'f-loop selezionato.
Il valore degli elementi sarà 0 per i collegamenti e ramoscelli rimanenti, che non fanno parte dell'f-loop selezionato.
Se la direzione della corrente del ramoscello del loop f selezionato è uguale a quella della corrente del link f-loop, il valore dell'elemento sarà +1.
Se la direzione della corrente di twig del loop f selezionato è opposta a quella della corrente del link f-loop, il valore dell'elemento sarà -1.
Procedura per trovare la matrice del ciclo fondamentale
Seguire questi passaggi per trovare la matrice del ciclo fondamentale di un dato grafo diretto.
Seleziona un albero di un dato grafico diretto.
Includendo un collegamento alla volta, otterremo un f-loop. Riempi i valori degli elementi corrispondenti a questo f-loop in una riga della matrice del loop fondamentale.
Ripetere il passaggio precedente per tutti i collegamenti.
Esempio
Dai un'occhiata al seguente albero di directed graph, che è considerato per la matrice di incidenza.

L'albero sopra contiene tre rami d, e & f. Quindi, i rami a, b e c saranno i collegamenti del Co-Albero corrispondente all'Albero sopra. Includendo un collegamento alla volta all'albero sopra, ne otterremo unof-loop. Quindi, ce ne saranno tref-loops, poiché sono presenti tre collegamenti. Questi tre f-loop sono mostrati nella figura seguente.
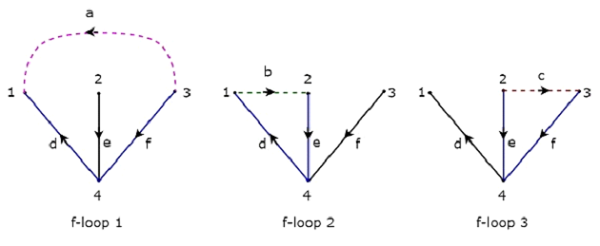
Nella figura sopra, i rami, che sono rappresentati con linee colorate, formano f-loop. Otterremo i valori degli elementi per riga della matrice Tie-set da ogni f-loop. Così laTieset matrix dell'Albero sopra considerato sarà
$$B = \begin{bmatrix}1 & 0 & 0 & -1 & 0 & -1\\0 & 1 & 0 & 1 & 1 & 0\\0 & 0 & 1 & 0 & -1 & 1 \end{bmatrix}$$
Le righe e le colonne della matrice sopra rappresentano i collegamenti e le diramazioni di un dato grafico diretto. L'ordine di questa matrice di incidenza è 3 × 6.
Il number of Fundamental loop matricesdi un grafo orientato sarà uguale al numero di alberi di quel grafo orientato. Perché ogni albero avrà una matrice del ciclo fondamentale.
Matrice di set di taglio fondamentale
Taglio fondamentale impostato o f-cut setè il numero minimo di rami che vengono rimossi da un grafico in modo tale che il grafico originale diventi due sottografi isolati. Il set f-cut contiene solo fileone twige uno o più link. Quindi, il numero di set f-cut sarà uguale al numero di ramoscelli.
Fundamental cut set matrix è rappresentato con la lettera C. Questa matrice fornisce la relazione tra le tensioni di diramazione e le tensioni di ramoscello.
Se sono presenti "n" nodi e rami "b" sono presenti in a directed graph, quindi il numero di ramoscelli presenti in un albero selezionato di un dato grafico sarà n-1. Quindi, la matrice del set di taglio fondamentale avrà righe "n-1" e colonne "b". Qui, righe e colonne corrispondono ai ramoscelli dell'albero selezionato e ai rami di un dato grafico. Quindi ilorder della matrice del set di taglio fondamentale sarà (n-1) × b.
Il elements of fundamental cut set matrix avrà uno di questi tre valori, +1, -1 e 0.
Il valore dell'elemento sarà +1 per il ramoscello dell'f-cutset selezionato.
Il valore degli elementi sarà 0 per i rimanenti ramoscelli e collegamenti, che non fanno parte dell'f-cutset selezionato.
Se la direzione della corrente di collegamento dell'insieme f-cut selezionato è uguale a quella della corrente del ramoscello f-cutset, il valore dell'elemento sarà +1.
Se la direzione della corrente di collegamento dell'insieme f-cut selezionato è opposta a quella della corrente del ramoscello f-cutset, il valore dell'elemento sarà -1.
Procedura per trovare la matrice del set di taglio fondamentale
Seguire questi passaggi per trovare la matrice dell'insieme di taglio fondamentale di un dato grafico diretto.
Selezionare un albero di un dato grafico diretto e rappresentare i collegamenti con le linee tratteggiate.
Rimuovendo un ramoscello e i collegamenti necessari alla volta, otterremo un set f-cut. Riempi i valori degli elementi corrispondenti a questo set di f-cut in una riga della matrice del set di tagli fondamentali.
Ripeti il passaggio precedente per tutti i ramoscelli.
Esempio
Considera lo stesso directed graph , di cui abbiamo discusso nella sezione della matrice di incidenza. Seleziona i rami d, e & f di questo grafico orientato come ramoscelli. Quindi, i rimanenti rami a, b & c di questo grafo diretto saranno i collegamenti.
Il twigs d, e & f sono rappresentati con linee continue e links a, b e c sono rappresentati con linee tratteggiate nella figura seguente.
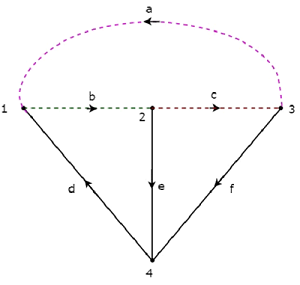
Rimuovendo un ramoscello e i collegamenti necessari alla volta, otterremo un set f-cut. Quindi, ci saranno tre set f-cut, poiché ci sono tre ramoscelli. Questi tref-cut sets sono mostrati nella figura seguente.

Avremo tre set f-cut rimuovendo un set di ramoscelli e collegamenti di C 1 , C 2 e C 3 . Otterremo i valori degli elementi di riga della matrice del set di taglio fondamentale da ciascun set di f-cut. Così lafundamental cut set matrix dell'Albero sopra considerato sarà
$$C = \begin{bmatrix}1 & -1 & 0 & 1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \end{bmatrix}$$
Le righe e le colonne della matrice precedente rappresentano i ramoscelli e i rami di un dato grafico diretto. L'ordine di questa matrice fondamentale del set di tagli è 3 × 6.
Il number of Fundamental cut set matricesdi un grafo orientato sarà uguale al numero di alberi di quel grafo orientato. Perché, ogni albero avrà una matrice di set di taglio fondamentale.
Superposition theoremsi basa sul concetto di linearità tra la risposta e l'eccitazione di un circuito elettrico. Afferma che la risposta in un particolare ramo di un circuito lineare quando più sorgenti indipendenti agiscono contemporaneamente è equivalente alla somma delle risposte dovute a ciascuna sorgente indipendente che agisce alla volta.
In questo metodo, considereremo solo one independent sourceAl tempo. Quindi, dobbiamo eliminare le rimanenti fonti indipendenti dal circuito. Possiamo eliminare le sorgenti di tensione cortocircuitando i loro due terminali e, analogamente, le sorgenti di corrente aprendo i loro due terminali.
Pertanto, dobbiamo trovare la risposta in un ramo particolare ‘n’ timesse ci sono "n" fonti indipendenti. La risposta in un particolare ramo potrebbe essere la corrente che scorre attraverso quel ramo o la tensione attraverso quel ramo.
Procedura del teorema di sovrapposizione
Segui questi passaggi per trovare la risposta in un particolare ramo usando il teorema di sovrapposizione.
Step 1 - Trova la risposta in un particolare ramo considerando una fonte indipendente ed eliminando le restanti fonti indipendenti presenti nella rete.
Step 2 - Ripetere il passaggio 1 per tutte le sorgenti indipendenti presenti nella rete.
Step 3 - Aggiungi tutte le risposte per ottenere la risposta complessiva in un particolare ramo quando tutte le fonti indipendenti sono presenti nella rete.
Esempio
Trova la corrente che scorre attraverso la resistenza da 20 Ω del seguente circuito usando superposition theorem.
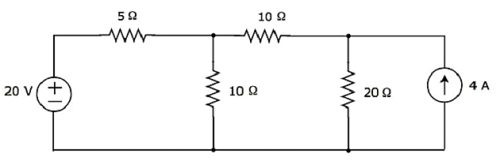
Step 1 - Troviamo la corrente che scorre attraverso la resistenza da 20 Ω considerando solo 20 V voltage source. In questo caso, possiamo eliminare la sorgente di corrente da 4 A rendendola a circuito aperto. Lo schema elettrico modificato è mostrato nella figura seguente.

C'è solo un nodo principale eccetto Ground nel circuito sopra. Quindi, possiamo usarenodal analysismetodo. La tensione del nodo V 1 è etichettata nella figura seguente. Qui, V 1 è la tensione dal nodo 1 rispetto a terra.
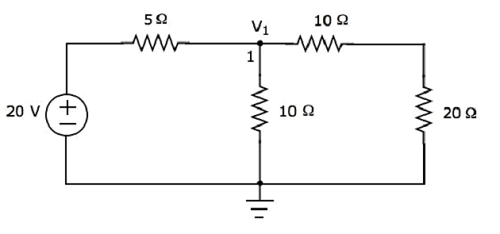
Il nodal equation al nodo 1 è
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1}{10 + 20} = 0$$
$$\Rightarrow \frac{6V_1 - 120 + 3V_1 + V_1}{30} = 0$$
$$\Rightarrow 10V_1 = 120$$
$$\Rightarrow V_1 = 12V$$
Il current flowing through 20 Ω resistor può essere trovato facendo la seguente semplificazione.
$$I_1 = \frac{V_1}{10 + 20}$$
Sostituisci il valore di V 1 nell'equazione precedente.
$$I_1 = \frac{12}{10 + 20} = \frac{12}{30} = 0.4 A$$
Pertanto, la corrente che scorre attraverso il resistore da 20 Ω è 0.4 A, quando si considera solo una sorgente di tensione di 20 V.
Step 2 - Troviamo la corrente che scorre attraverso la resistenza da 20 Ω considerando solo 4 A current source. In questo caso possiamo eliminare la sorgente di tensione a 20 V facendola cortocircuitare. Lo schema elettrico modificato è mostrato nella figura seguente.
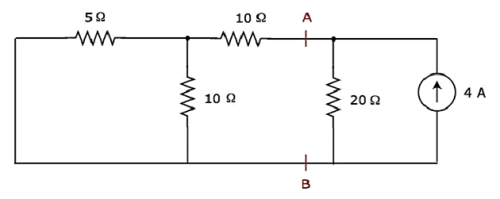
Nel circuito sopra, ci sono tre resistori a sinistra dei terminali A e B. Possiamo sostituire questi resistori con uno singolo equivalent resistor. Qui, i resistori da 5 Ω e 10 Ω sono collegati in parallelo e l'intera combinazione è in serie con il resistore da 10 Ω.
Il equivalent resistance a sinistra dei terminali A e B.
$$R_{AB} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$
Lo schema circuitale semplificato è mostrato nella figura seguente.
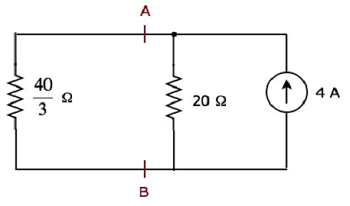
Possiamo trovare la corrente che scorre attraverso la resistenza da 20 Ω, usando current division principle.
$$I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$
Sostituto $I_S = 4A,\: R_1 = \frac{40}{3} \Omega$ e $R_2 = 20 \Omega$ nell'equazione precedente.
$$I_2 = 4 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup = 4 \lgroup \frac{40}{100} \rgroup = 1.6 A$$
Pertanto, la corrente che scorre attraverso il resistore da 20 Ω è 1.6 A, quando viene considerata solo la sorgente di corrente 4 A.
Step 3 - Otterremo la corrente che scorre attraverso la resistenza da 20 Ω del circuito dato eseguendo il addition of two currents che abbiamo ottenuto al passaggio 1 e al passaggio 2. Matematicamente, può essere scritto come
$$I = I_1 + I_2$$
Sostituisci i valori di I 1 e I 2 nell'equazione precedente.
$$I = 0.4 + 1.6 = 2 A$$
Pertanto, la corrente che scorre attraverso il resistore da 20 Ω di un dato circuito è 2 A.
Note - Non possiamo applicare direttamente il teorema di sovrapposizione per trovare la quantità di powererogato a qualsiasi resistore presente in un circuito lineare, semplicemente aggiungendo le potenze erogate a quel resistore dovute a ciascuna sorgente indipendente. Piuttosto, possiamo calcolare la corrente totale che scorre o la tensione attraverso quel resistore usando il teorema di sovrapposizione e da questo, possiamo calcolare la quantità di potenza fornita a quel resistore usando$I^2 R$ o $\frac{V^2}{R}$.
Thevenin’s theoremafferma che qualsiasi rete o circuito lineare a due terminali può essere rappresentato con una rete o circuito equivalente, che consiste in una sorgente di tensione in serie con un resistore. È noto come il circuito equivalente di Thevenin. Un circuito lineare può contenere sorgenti indipendenti, sorgenti dipendenti e resistori.
Se il circuito contiene più sorgenti indipendenti, sorgenti dipendenti e resistori, la risposta in un elemento può essere facilmente trovata sostituendo l'intera rete a sinistra di quell'elemento con un Thevenin’s equivalent circuit.
Il response in an element può essere la tensione attraverso quell'elemento, la corrente che fluisce attraverso quell'elemento o la potenza dissipata attraverso quell'elemento.
Questo concetto è illustrato nelle figure seguenti.
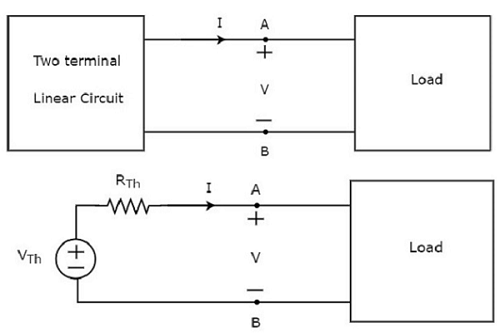
Thevenin’s equivalent circuitassomiglia a una pratica sorgente di tensione. Quindi, ha una sorgente di tensione in serie con un resistore.
La sorgente di tensione presente nel circuito equivalente di Thevenin è chiamata tensione equivalente di Thevenin o semplicemente Thevenin’s voltage, VTh.
Il resistore presente nel circuito equivalente di Thevenin è chiamato resistore equivalente di Thevenin o semplicemente Thevenin’s resistor, RTh.
Metodi per trovare il circuito equivalente di Thevenin
Esistono tre metodi per trovare un circuito equivalente di Thevenin. Basato sultype of sourcespresenti nella rete, possiamo scegliere uno di questi tre metodi. Ora, discutiamo due metodi uno per uno. Discuteremo il terzo metodo nel prossimo capitolo.
Metodo 1
Segui questi passaggi per trovare il circuito equivalente di Thevenin, quando solo il sources of independent type sono presenti.
Step 1 - Considerare lo schema elettrico aprendo i terminali rispetto ai quali si trova il circuito equivalente di Thevenin.
Step 2 - Trova il voltaggio di Thevenin VTh attraverso i terminali aperti del circuito di cui sopra.
Step 3 - Trova la resistenza di Thevenin RTh attraverso i terminali aperti del circuito suddetto eliminando le sorgenti indipendenti in esso presenti.
Step 4 - Disegna il file Thevenin’s equivalent circuitcollegando una tensione di Thevenin V Th in serie con una resistenza di Thevenin R Th .
Ora, possiamo trovare la risposta in un elemento che si trova sul lato destro del circuito equivalente di Thevenin.
Esempio
Trova la corrente che scorre attraverso il resistore da 20 Ω trovando prima a Thevenin’s equivalent circuit a sinistra dei terminali A e B.
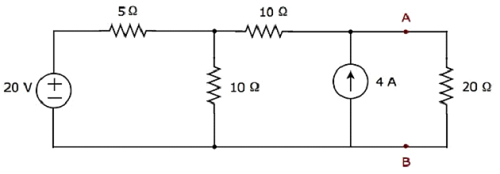
Step 1 - Per trovare il circuito equivalente di Thevenin sul lato sinistro dei terminali A e B, dovremmo rimuovere la resistenza da 20 Ω dalla rete opening the terminals A & B. Lo schema elettrico modificato è mostrato nella figura seguente.
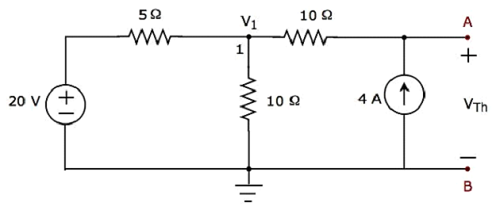
Step 2 - Calcolo di Thevenin’s voltage VTh.
C'è solo un nodo principale eccetto Ground nel circuito sopra. Quindi, possiamo usarenodal analysismetodo. La tensione del nodo V 1 e la tensione di Thevenin V Th sono indicate nella figura sopra. Qui, V 1 è la tensione dal nodo 1 rispetto a Ground e V Th è la tensione attraverso la sorgente di corrente 4 A.
Il nodal equation al nodo 1 è
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} - 4 = 0$$
$$\Rightarrow \frac{2V_1 - 40 + V_1 - 40}{10} = 0$$
$$\Rightarrow 3V_1 - 80 = 0$$
$$\Rightarrow V_1 = \frac{80}{3}V$$
La tensione sul resistore da 10 Ω del ramo in serie è
$$V_{10 \Omega} = (-4)(10) = -40V$$
Ci sono due maglie nel circuito sopra. IlKVL equation intorno alla seconda maglia è
$$V_1 - V_{10 \Omega} - V_{Th} = 0$$
Sostituisci i valori di $V_1$ e $V_{10 \Omega}$ nell'equazione precedente.
$$\frac{80}{3} - (-40) - V_{Th} = 0$$
$$V_{Th} = \frac{80 + 120}{3} = \frac{200}{3}V$$
Pertanto, il voltaggio di Thevenin è $V_{Th} = \frac{200}{3}V$
Step 3 - Calcolo di Thevenin’s resistance RTh.
Cortocircuitare la sorgente di tensione e aprire il circuito della sorgente di corrente del circuito di cui sopra per calcolare la resistenza di Thevenin R Th attraverso i terminali A e B.modified circuit diagram è mostrato nella figura seguente.
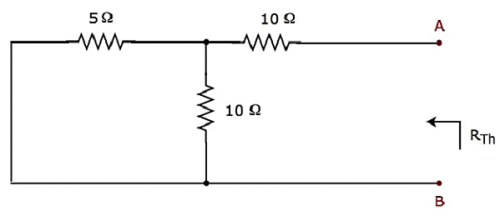
La resistenza di Thevenin sui terminali A e B sarà
$$R_{Th} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$
Pertanto, la resistenza di Thevenin è $\mathbf {R_{Th} = \frac{40}{3} \Omega}$.
Step 4- Il circuito equivalente di Thevenin è posto a sinistra dei terminali A e B nel circuito dato. Questo schema elettrico è mostrato nella figura seguente.

La corrente che scorre attraverso il resistore da 20 Ω può essere trovata sostituendo i valori di V Th , R Th e R nella seguente equazione.
$$l = \frac{V_{Th}}{R_{Th} + R}$$
$$l = \frac{\frac{200}{3}}{\frac{40}{3} + 20} = \frac{200}{100} = 2A$$
Pertanto, la corrente che scorre attraverso il resistore da 20 Ω è 2 A.
Metodo 2
Segui questi passaggi per trovare il circuito equivalente di Thevenin, quando il file sources of both independent type and dependent type sono presenti.
Step 1 - Considerare lo schema elettrico aprendo i terminali rispetto ai quali si trova il circuito equivalente di Thevenin.
Step 2 - Trova il voltaggio di Thevenin VTh attraverso i terminali aperti del circuito di cui sopra.
Step 3 - Trova la corrente di cortocircuito ISC cortocircuitando i due terminali aperti del circuito di cui sopra.
Step 4 - Trova la resistenza di Thevenin RTh utilizzando la seguente formula.
$$R_{Th} = \frac{V_{Th}}{I_{SC}}$$
Step 5 - Disegna il file Thevenin’s equivalent circuitcollegando una tensione di Thevenin V Th in serie con una resistenza di Thevenin R Th .
Ora, possiamo trovare la risposta in un elemento che si trova sul lato destro del circuito equivalente di Thevenin.
Norton’s theoremè simile al teorema di Thevenin. Afferma che qualsiasi rete o circuito lineare a due terminali può essere rappresentato con una rete o circuito equivalente, che consiste in una sorgente di corrente in parallelo con un resistore. È noto comeNorton’s equivalent circuit. Un circuito lineare può contenere sorgenti indipendenti, sorgenti dipendenti e resistori.
Se un circuito ha più sorgenti indipendenti, sorgenti dipendenti e resistori, la risposta in un elemento può essere facilmente trovata sostituendo l'intera rete a sinistra di quell'elemento con un Norton’s equivalent circuit.
Il response in an element può essere la tensione attraverso quell'elemento, la corrente che scorre attraverso quell'elemento o la potenza dissipata attraverso quell'elemento.
Questo concetto è illustrato nelle figure seguenti.
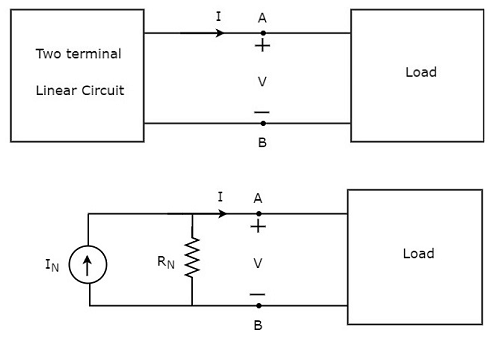
Norton’s equivalent circuitassomiglia a una pratica sorgente di corrente. Quindi, ha una sorgente di corrente in parallelo con un resistore.
La sorgente di corrente presente nel circuito equivalente di Norton è chiamata corrente equivalente di Norton o semplicemente Norton’s current IN.
Il resistore presente nel circuito equivalente di Norton è chiamato resistore equivalente di Norton o semplicemente Norton’s resistor RN.
Metodi per trovare il circuito equivalente di Norton
Ci sono three methodsper trovare un circuito equivalente di Norton. In base al tipo di sorgenti presenti nella rete, possiamo scegliere uno di questi tre metodi. Ora, discutiamo questi tre metodi uno per uno.
Metodo 1
Segui questi passaggi per trovare il circuito equivalente di Norton, quando solo il sources of independent type sono presenti.
Step 1 - Considerare lo schema elettrico aprendo i terminali rispetto ai quali si trova il circuito equivalente del Norton.
Step 2 - Trova la corrente del Norton IN cortocircuitando i due terminali aperti del circuito di cui sopra.
Step 3 - Trova la resistenza del Norton RNattraverso i terminali aperti del circuito considerato nella Fase 1 eliminando le sorgenti indipendenti in esso presenti. La resistenza di NortonRN sarà lo stesso della resistenza di Thevenin RTh.
Step 4 - Disegna il file Norton’s equivalent circuitcollegando IN attuale di un Norton in parallelo con la resistenza di Norton R N .
Ora, possiamo trovare la risposta in un elemento che si trova sul lato destro del circuito equivalente di Norton.
Metodo 2
Segui questi passaggi per trovare il circuito equivalente di Norton, quando il file sources of both independent type and dependent type sono presenti.
Step 1 - Considerare lo schema elettrico aprendo i terminali rispetto ai quali si trova il circuito equivalente del Norton.
Step 2 - Trova la tensione del circuito aperto VOC attraverso i terminali aperti del circuito di cui sopra.
Step 3 - Trova la corrente del Norton IN cortocircuitando i due terminali aperti del circuito di cui sopra.
Step 4 - Trova la resistenza di Norton RN utilizzando la seguente formula.
$$R_N = \frac{V_{OC}}{I_N}$$
Step 5- Disegna il circuito equivalente di Norton collegando la corrente di Norton I N in parallelo con la resistenza R N di Norton .
Ora, possiamo trovare la risposta in un elemento che si trova sul lato destro del circuito equivalente di Norton.
Metodo 3
Questo è un metodo alternativo per trovare il circuito equivalente di un Norton.
Step 1 - Trova un file Thevenin’s equivalent circuittra i due terminali desiderati. Sappiamo che consiste in una sorgente di tensione di Thevenin, V Th e un resistore di Thevenin, R Th .
Step 2 - Applica source transformation techniqueal circuito equivalente di Thevenin sopra. Otterremo il circuito equivalente di Norton. Qui,
L'attuale di Norton,
$$I_N = \frac{V_{Th}}{R_{Th}}$$
La resistenza di Norton,
$$R_N = R_{Th}$$
Questo concetto è illustrato nella figura seguente.
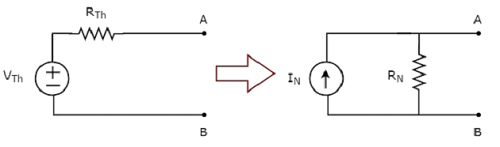
Ora, possiamo trovare la risposta in un elemento posizionando il circuito equivalente di Norton a sinistra di quell'elemento.
Note- Allo stesso modo, possiamo trovare il circuito equivalente di Thevenin trovando prima il circuito equivalente di Norton e quindi applicandovi la tecnica di trasformazione della sorgente. Questo concetto è illustrato nella figura seguente.
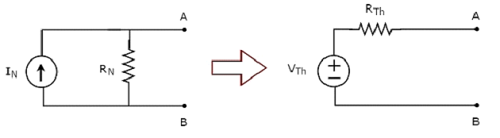
Questo è il metodo 3 per trovare un circuito equivalente di Thevenin.
Esempio
Trova la corrente che scorre attraverso il resistore da 20 Ω trovando prima a Norton’s equivalent circuit a sinistra dei terminali A e B.
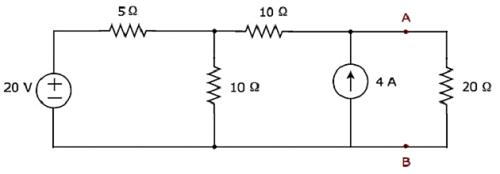
Cerchiamo di risolvere questo problema utilizzando Method 3.
Step 1- Nel capitolo precedente, abbiamo calcolato il circuito equivalente di Thevenin sul lato sinistro dei terminali A e B. Ora possiamo usare questo circuito. È mostrato nella figura seguente.
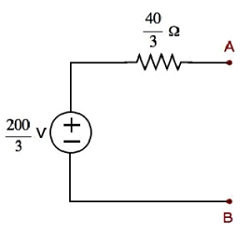
Qui, la tensione di Thevenin, $V_{Th} = \frac{200}{3} V$ e la resistenza di Thevenin, $R_{Th} = \frac{40}{3} \Omega$
Step 2 - Applica source transformation techniqueal circuito equivalente di Thevenin sopra. Sostituisci i valori di V Th e R Th nella seguente formula diNorton’s current.
$$I_N = \frac{V_{Th}}{R_{Th}}$$
$$I_N = \frac{\frac{200}{3}}{\frac{40}{3}} = 5A$$
Pertanto, l'attuale I N di Norton è5 A.
Sappiamo che la resistenza di Norton, R N è la stessa di quella di Thevenin R Th .
$$\mathbf {R_N = \frac{40}{3} \Omega}$$
Il circuito equivalente di Norton corrispondente al circuito equivalente di Thevenin di cui sopra è mostrato nella figura seguente.
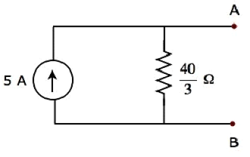
Ora, posiziona il circuito equivalente di Norton a sinistra dei terminali A e B del circuito dato.
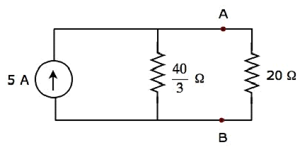
Usando current division principle, la corrente che scorre attraverso il resistore da 20 Ω sarà
$$I_{20 \Omega} = 5 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup$$
$$I_{20 \Omega} = 5 \lgroup \frac{40}{100} \rgroup = 2A$$
Pertanto, la corrente che scorre attraverso il resistore da 20 Ω è 2 A.
La quantità di potenza ricevuta da un carico è un parametro importante nelle applicazioni elettriche ed elettroniche. Nei circuiti DC, possiamo rappresentare il carico con un resistore avente una resistenza di R L ohm. Allo stesso modo, nei circuiti AC, possiamo rappresentarlo con un carico complesso avente un'impedenza di Z L ohm.
Maximum power transfer theorem afferma che la sorgente di tensione CC fornirà la massima potenza al resistore di carico variabile solo quando la resistenza di carico è uguale alla resistenza della sorgente.
Allo stesso modo, Maximum power transfer theorem afferma che la sorgente di tensione CA fornirà la massima potenza al carico complesso variabile solo quando l'impedenza di carico è uguale al coniugato complesso dell'impedenza della sorgente.
In questo capitolo, discutiamo del teorema del trasferimento di potenza massima per i circuiti CC.
Dimostrazione del teorema del trasferimento di potenza massima
Sostituire qualsiasi rete o circuito lineare a due terminali sul lato sinistro del resistore a carico variabile avente una resistenza di R L ohm con un circuito equivalente di Thevenin. Sappiamo che il circuito equivalente di Thevenin assomiglia a una pratica sorgente di tensione.
Questo concetto è illustrato nelle figure seguenti.
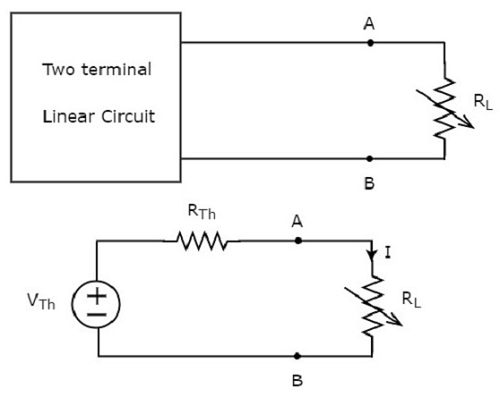
La quantità di potenza dissipata attraverso il resistore di carico è
$$P_L = I^2 R_L$$
Sostituto $I = \frac{V_{Th}}{R_{Th} + R_L}$ nell'equazione precedente.
$$P_L = \lgroup \frac{V_{Th}}{(R_{Th} + R_L)} \rgroup ^2 R_L$$
$\Rightarrow P_L = {V_{Th}}^2 \lbrace \frac{R_L}{(R_{Th} + R_L)^2} \rbrace$ Equation 1
Condizione per il massimo trasferimento di potenza
Per il massimo o il minimo, la derivata prima sarà zero. Quindi, differenziare l'equazione 1 rispetto a R L e renderla uguale a zero.
$$\frac{dP_L}{dR_L} = {V_{Th}}^2 \lbrace \frac{(R_{Th} + R_L)^2 \times 1 - R_L \times 2(R_{Th} + R_L)}{(R_{Th} + R_L)^4} \rbrace = 0$$
$$\Rightarrow (R_{Th} + R_L)^2 -2R_L(R_{Th} + R_L) = 0$$
$$\Rightarrow (R_{Th} + R_L)(R_{Th} + R_L - 2R_L) = 0$$
$$\Rightarrow (R_{Th} - R_L) = 0$$
$$\Rightarrow R_{Th} = R_L\:or\:R_L = R_{Th}$$
quindi, il condition for maximum power la dissipazione attraverso il carico è $R_L = R_{Th}$. Ciò significa che se il valore della resistenza di carico è uguale al valore della resistenza della sorgente, cioè la resistenza di Thevenin, la potenza dissipata attraverso il carico sarà del valore massimo.
Il valore di Maximum Power Transfer
Sostituto $R_L = R_{Th}\:\&\:P_L = P_{L, Max}$ nell'equazione 1.
$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{(R_{Th} + R_{Th})^2} \rbrace$$
$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{4 {R_{Th}}^2} \rbrace$$
$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$
$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{L}}, \: since \: R_{L} = R_{Th}$$
quindi, il maximum amount of power trasferito al carico è
$$P_{L, Max} = \frac{{V_{Th}}^2}{4R_{L}} = \frac{{V_{Th}}^2}{4R_{Th}}$$
Efficienza del massimo trasferimento di potenza
Possiamo calcolare l'efficienza del massimo trasferimento di potenza, $\eta_{Max}$ utilizzando la seguente formula.
$\eta_{Max} = \frac{P_{L, Max}}{P_S}$ Equation 2
Dove,
$P_{L, Max}$ è la quantità massima di potenza trasferita al carico.
$P_S$ è la quantità di energia generata dalla sorgente.
Il amount of power generated dalla fonte è
$$P_S = I^2 R_{Th} + I^2 R_L$$
$$\Rightarrow P_S = 2 I^2 R_{Th},\:since\:R_{L} = R_{Th}$$
Sostituto $I = \frac{V_{Th}}{2 R_{Th}}$ nell'equazione precedente.
$$P_S = 2\lgroup \frac{V_{Th}}{2 R_{Th}} \rgroup ^2 R_{Th}$$
$$\Rightarrow P_S = 2\lgroup \frac{{V_{Th}}^2}{4 {R_{Th}}^2} \rgroup R_{Th}$$
$$\Rightarrow P_S = \frac{{V_{Th}}^2}{2 R_{Th}}$$
Sostituisci i valori di $P_{L, Max}$ e $P_S$ nell'equazione 2.
$$\eta_{Max} = \frac{\lgroup \frac{{V_{Th}}^2}{4R_{Th}} \rgroup}{\lgroup \frac{{V_{Th}}^2}{2R_{Th}}\rgroup}$$
$$\Rightarrow \eta_{Max} = \frac{1}{2}$$
Possiamo rappresentare l'efficienza del massimo trasferimento di potenza in termini di percentage come segue -
$$\% \eta_{Max} = \eta_{Max} \times 100\%$$
$$\Rightarrow \% \eta_{Max} = \lgroup \frac{1}{2} \rgroup \times 100\%$$
$$\Rightarrow \% \eta_{Max} = 50\%$$
Pertanto, l'efficienza del massimo trasferimento di potenza è 50 %.
Esempio
Trovare la maximum powererogabile al resistore di carico R L del circuito mostrato nella figura seguente.
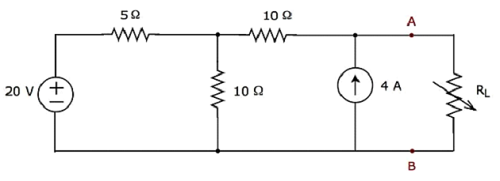
Step 1- Nel capitolo Teorema di Thevenin, abbiamo calcolato il circuito equivalente di Thevenin sul lato sinistro dei terminali A e B. Ora possiamo usare questo circuito. È mostrato nella figura seguente.
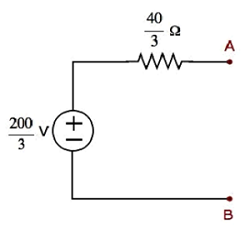
Ecco, il voltaggio di Thevenin $V_{Th} = \frac{200}{3}V$ e la resistenza di Thevenin $R_{Th} = \frac{40}{3} \Omega$
Step 2- Sostituire la parte del circuito, che si trova sul lato sinistro dei terminali A e B del circuito dato, con il circuito equivalente di Thevenin di cui sopra. Lo schema circuitale risultante è mostrato nella figura seguente.

Step 3- Possiamo trovare la potenza massima che verrà erogata al resistore di carico, R L utilizzando la seguente formula.
$$P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$
Sostituto $V_{Th} = \frac{200}{3}V$ e $R_{Th} = \frac{40}{3} \Omega$ nella formula sopra.
$$P_{L, Max} = \frac{\lgroup \frac{200}{3} \rgroup ^ 2}{4 \lgroup \frac{40}{3}\rgroup } $$
$$P_{L, Max} = \frac{250}{3} W$$
quindi, il maximum power che sarà fornito al resistore di carico RL del circuito dato è $\mathbf {\frac{250}{3}}$ W
Se l'uscita di un circuito elettrico per un ingresso varia rispetto al tempo, si chiama come time response. Il tempo di risposta consiste nel seguire due parti.
- Risposta transitoria
- Risposta allo stato stazionario
In questo capitolo, discutiamo prima di queste due risposte e poi osserviamo queste due risposte in un circuito RL in serie, quando è eccitato da una sorgente di tensione CC.
Risposta transitoria
Dopo aver applicato un ingresso a un circuito elettrico, l'uscita impiega un certo tempo per raggiungere lo stato stazionario. Quindi, l'uscita sarà in uno stato transitorio fino a quando non passa a uno stato stabile. Pertanto, la risposta del circuito elettrico durante lo stato transitorio è nota cometransient response.
La risposta transitoria sarà zero per grandi valori di "t". Idealmente, questo valore di "t" dovrebbe essere infinito. Ma praticamentefive time constants sono sufficienti.
Presenza o assenza di transitori
Transitori si verificano nella risposta a causa di sudden changenelle sorgenti che vengono applicate al circuito elettrico e / o per azione di commutazione. Sono possibili due azioni di commutazione. Quelli sono interruttore di apertura e interruttore di chiusura.
Il transient parte lo farà not presentnella risposta di un circuito elettrico o di una rete, se contiene solo resistenze. Perchéresistor sta avendo la capacità di regolare qualsiasi quantità di tensione e corrente.
Il transient part occurs nella risposta di un circuito elettrico o di una rete a causa della presenza di elementi di accumulo di energia come inductor and capacitor. Perché non possono cambiare istantaneamente l'energia immagazzinata in quegli elementi.
Comportamento dell'induttore
Supponiamo che l'azione di commutazione avvenga a t = 0.Inductor currentnon cambia istantaneamente quando avviene l'azione di commutazione. Ciò significa che il valore della corrente dell'induttore subito dopo l'azione di commutazione sarà uguale a quello appena prima dell'azione di commutazione.
Matematicamente, può essere rappresentato come
$$i_L (0^+) = i_L (0^-)$$
Comportamento del condensatore
Il capacitor voltagenon cambia istantaneamente come la corrente dell'induttore, quando ha luogo l'azione di commutazione. Ciò significa che il valore della tensione del condensatore subito dopo l'azione di commutazione sarà uguale a quello appena prima dell'azione di commutazione.
Matematicamente, può essere rappresentato come
$$v_c (0^+) = v_c (0^-)$$
Risposta allo stato stazionario
La parte della risposta temporale che rimane anche dopo che la risposta transitoria è diventata valore zero per valori grandi di 't' è nota come steady state response. Ciò significa che non ci sarà alcuna parte transitoria nella risposta durante lo stato stazionario.
Comportamento dell'induttore
Se la sorgente indipendente è collegata al circuito elettrico o alla rete avente uno o più induttori e resistori (opzionali) per un lungo periodo, si dice che quel circuito elettrico o rete sia in stato stazionario. Pertanto, l'energia immagazzinata negli induttori di quel circuito elettrico è massima e costante.
Matematicamente, può essere rappresentato come
$W_L = \frac{L {i_L}^2}{2} = $ Massimo e costante
$\Rightarrow i_L = $ Massimo e costante
Pertanto, l'induttore funge da constant current source in stato stazionario.
La tensione attraverso l'induttore sarà
$$V_L = L \frac{di_{L}}{dt} = 0V$$
Quindi, l'induttore funge da short circuit in stato stazionario.
Comportamento del condensatore
Se la sorgente indipendente è collegata al circuito elettrico o alla rete avente uno o più condensatori e resistenze (opzionali) per un lungo periodo, si dice che quel circuito elettrico o rete sia in stato stazionario. Pertanto, l'energia immagazzinata nei condensatori di quel circuito elettrico è massima e costante.
Matematicamente, può essere rappresentato come
$W_c = \frac{C{v_c}^2}{2} = $ Massimo e costante
$\Rightarrow v_c = $Massimo e costante
Pertanto, il condensatore funge da constant voltage source in stato stazionario.
La corrente che scorre attraverso il condensatore sarà
$$i_c = C\frac{dv_c}{dt} = 0A$$
Quindi, il condensatore agisce come un file open circuit in stato stazionario.
Trovare la risposta del circuito serie RL
Considera quanto segue series RL circuit diagramma.
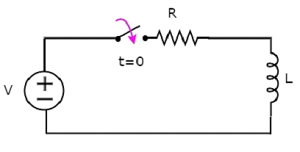
Nel circuito sopra, il switch Era tenuto openfino a t = 0 ed era chiusa a t = 0. Quindi, la sorgente di tensione continua avente V volt non è collegata al circuito della serie RL fino a questo istante. Quindi c'èno initial current scorre attraverso l'induttore.
Lo schema del circuito, quando il switch è dentro closed la posizione è mostrata nella figura seguente.
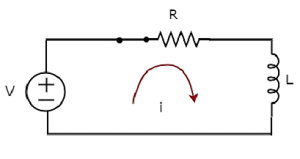
Ora, la corrente i fluisce nell'intero circuito, poiché la sorgente di tensione CC ha V volt è collegato al circuito della serie RL.
Ora, applica KVL intorno al ciclo.
$$V = Ri + L \frac{di}{dt}$$
$\frac{di}{dt} + \lgroup \frac{R}{L} \rgroup i = \frac{V}{L}$Equation 1
L'equazione di cui sopra è un'equazione differenziale del primo ordine ed è nella forma di
$\frac{dy}{dt} + Py = Q$Equation 2
Di comparing Equazione 1 ed Equazione 2, otterremo le seguenti relazioni.
$$x = t$$
$$y = i$$
$$P = \frac{R}{L}$$
$$Q = \frac{V}{L}$$
Il solution dell'equazione 2 sarà
$ye^{\int p dx} = \int Q e^{\int p dx} dx + k$Equation 3
Dove, k è la costante.
Sostituisci, i valori di x, y, P & Q nell'equazione 3.
$ie^{\int {\lgroup \frac{R}{L} \rgroup}dt} = \int (\frac{V}{L}) \lgroup e^{\int {\lgroup \frac{R}{L} \rgroup}dt} \rgroup dt + k$
$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \int e^{\lgroup \frac{R}{L} \rgroup t} dt + k$
$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \lbrace \frac{e^{\lgroup \frac{R}{L} \rgroup}t}{\frac{R}{L}} \rbrace + k$
$\Rightarrow i = \frac{V}{R} + k e^{-\lgroup \frac{R}{L} \rgroup}t$Equation 4
Sappiamo che non c'è corrente iniziale nel circuito. Quindi, sostituire, t = 0 e = 0 nell'equazione 4 per trovare il valore della costante k.
$$0 = \frac{V}{R} + ke^{-\lgroup \frac{R}{L} \rgroup(0)}$$
$$0 = \frac{V}{R} + k(1)$$
$$k = - \frac{V}{R}$$
Sostituisci il valore di k nell'equazione 4.
$$i = \frac{V}{R} + \lgroup - \frac{V}{R} \rgroup e^{-\lgroup \frac{R}{L} \rgroup t}$$
$$i = \frac{V}{R} - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$$
quindi, il current che scorre attraverso il circuito è
$i = - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t} + \frac{V}{R}$Equation 5
Quindi, la risposta del circuito della serie RL, quando è eccitato da una sorgente di tensione CC, ha i seguenti due termini.
Il primo termine $-\frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$ corrisponde con il transient response.
Il secondo termine $\frac{V}{R}$ corrisponde con il steady state response. Queste due risposte sono mostrate nella figura seguente.
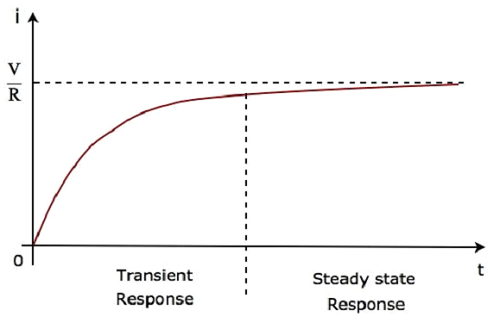
Possiamo riscrivere l'equazione 5 come segue:
$i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{R}{L} \rgroup t} \rgroup$
$\Rightarrow i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{t}{\tau} \rgroup} \rgroup$Equation 6
Dove, τ è il time constant e il suo valore è uguale a $\frac{L}{R}$.
Sia l'equazione 5 che l'equazione 6 sono uguali. Tuttavia, possiamo facilmente comprendere la forma d'onda di cui sopra della corrente che fluisce attraverso il circuito dall'equazione 6 sostituendo alcuni valori dit come 0, τ, 2τ, 5τ, ecc.
Nella suddetta forma d'onda della corrente che fluisce attraverso il circuito, la risposta transitoria presenterà fino a cinque costanti di tempo da zero, mentre la risposta di stato stazionario sarà presente da cinque costanti di tempo in poi.
Nel capitolo precedente, abbiamo discusso la risposta ai transienti e la risposta allo stato stazionario del circuito CC. In questo capitolo, discutiamo diresponse of AC circuit. Anche qui saranno utili i concetti sia di risposta transitoria che di risposta allo stato stazionario, che abbiamo discusso nel capitolo precedente.
Trovare la risposta del circuito serie RL
Considera quanto segue series RL circuit diagramma.

Nel circuito sopra, il switch Era tenuto openfino a t = 0 ed era chiuso a t = 0 . Quindi, la sorgente di tensione AC avente una tensione di picco di V m volt non è collegata al circuito della serie RL fino a questo istante. Quindi c'èno initial current scorre attraverso l'induttore.
Lo schema del circuito, quando il switch è dentro closed posizione, è mostrato nella figura seguente.
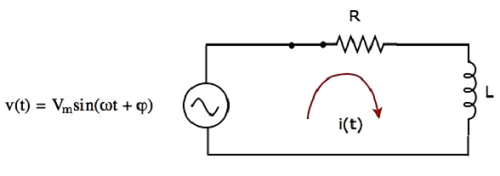
Ora, la corrente i (t) scorre nell'intero circuito, poiché la sorgente di tensione CA con una tensione di picco di V m volt è collegata al circuito della serie RL.
Sappiamo che la corrente i (t) che scorre attraverso il circuito di cui sopra avrà due termini, uno che rappresenta la parte transitoria e l'altro termine rappresenta lo stato stazionario.
Matematicamente, può essere rappresentato come
$i(t) = i_{Tr}(t) + i_{ss}(t)$Equation 1
Dove,
$i_{Tr}(t)$ è la risposta transitoria della corrente che scorre attraverso il circuito.
$i_{ss}(t)$ è la risposta allo stato stazionario della corrente che scorre attraverso il circuito.
Nel capitolo precedente, abbiamo ottenuto la risposta transitoria della corrente che scorre attraverso il circuito della serie RL. È sotto forma di$Ke^{-\lgroup \frac{t}{\tau} \rgroup}$.
Sostituto $i_{Tr}(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup}$ nell'equazione 1.
$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + i_{ss}(t)$Equation 2
Calcolo della corrente allo stato stazionario
Se un segnale sinusoidale viene applicato come ingresso a un circuito elettrico lineare, allora produce un'uscita di stato stazionario, che è anche un sinusoidal signal. Entrambi i segnali sinusoidali in ingresso e in uscita avranno la stessa frequenza, ma ampiezze e angoli di fase differenti.
Possiamo calcolare la risposta allo stato stazionario di un circuito elettrico, quando è eccitato da una sorgente di tensione sinusoidale utilizzando Laplace Transform approach.
Lo schema circuitale del dominio s, quando il switch è dentro closed posizione, è mostrato nella figura seguente.
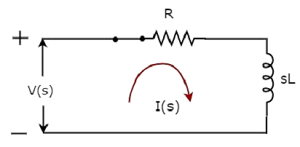
Nel circuito sopra, tutte le quantità e i parametri sono rappresentati in s-domain. Queste sono le trasformate di Laplace di grandezze e parametri nel dominio del tempo.
Il Transfer function del circuito sopra è
$$H(s) = \frac{I(s)}{V(s)}$$
$$\Rightarrow H(s) = \frac{1}{Z(s)}$$
$$\Rightarrow H(s) = \frac{1}{R + sL}$$
Sostituto $s = j \omega$ nell'equazione precedente.
$$H(j \omega) = \frac{1}{R + j \omega L}$$
Magnitude of $\mathbf{\mathit{H(j \omega)}}$ è
$$|H(j \omega)| = \frac{1}{\sqrt{R^2 + {\omega}^2}L^2}$$
Phase angle of $\mathbf{\mathit{H(j \omega)}}$ è
$$\angle H(j \omega) = -tan^{-1} \lgroup \frac{\omega L}{R} \rgroup$$
Otterremo il file steady state current $i_{ss}(t)$ eseguendo i due passaggi seguenti:
Moltiplicare la tensione di picco della tensione sinusoidale di ingresso e l'ampiezza di $H(j \omega)$.
Aggiungere gli angoli di fase della tensione sinusoidale di ingresso e $H(j \omega)$.
Il steady state current $i_{ss}(t)$ sarà
$$i_{ss}(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Sostituisci il valore di $i_{ss}(t)$ nell'equazione 2.
$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 3
Sappiamo che non c'è corrente iniziale nel circuito. Quindi, sostituire t = 0 & i (t) = 0 nell'equazione 3 per trovare il valore della costante K.
$$0 = Ke^{-\lgroup \frac{0}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega (0) + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
$$\Rightarrow 0 = K + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
$$\Rightarrow K = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Sostituisci il valore di K nell'equazione 3.
$i(t) = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup e^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 4
L'equazione 4 rappresenta la corrente che scorre attraverso il circuito della serie RL, quando è eccitata da una sorgente di tensione sinusoidale. Ha due termini. Il primo e il secondo termine rappresentano rispettivamente la risposta transitoria e la risposta allo stato stazionario della corrente.
Noi possiamo neglect the first termdell'equazione 4 perché il suo valore sarà molto inferiore a uno. Quindi, la corrente risultante che scorre attraverso il circuito sarà
$$i(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Contiene solo il file steady state term. Quindi, possiamo trovare solo la risposta allo stato stazionario dei circuiti CA e trascurarne la risposta transitoria.
Resonancesi verifica nei circuiti elettrici a causa della presenza di elementi che immagazzinano energia come induttore e condensatore. È il concetto fondamentale su cui i ricevitori radio e TV sono progettati in modo tale da poter selezionare solo la frequenza della stazione desiderata.
Ci sono two typesdi risonanze, vale a dire risonanza in serie e risonanza parallela. Questi sono classificati in base agli elementi di rete collegati in serie o in parallelo. In questo capitolo, discutiamo della risonanza in serie.
Schema del circuito di risonanza in serie
Se la risonanza si verifica nel circuito RLC in serie, viene chiamata come Series Resonance. Considera quanto segueseries RLC circuit, che è rappresentato nel dominio dei fasori.
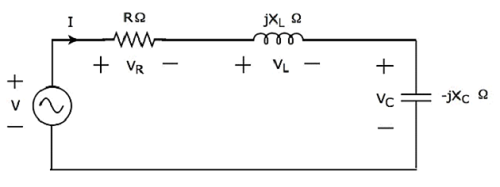
Qui, gli elementi passivi come resistenza, induttore e condensatore sono collegati in serie. Questa intera combinazione è dentroseries con la sorgente di tensione sinusoidale in ingresso.
Applicare KVL intorno al ciclo.
$$V - V_R - V_L - V_C = 0$$
$$\Rightarrow V - IR - I(j X_L) - I(-j X_C) = 0$$
$$\Rightarrow V = IR + I(j X_L) + I(-j X_C)$$
$\Rightarrow V = I[R + j(X_L - X_C)]$Equation 1
L'equazione di cui sopra ha la forma di V = IZ.
quindi, il impedance Z del circuito di serie RLC sarà
$$Z = R + j(X_L - X_C)$$
Parametri e grandezze elettriche in risonanza
Ora, deriviamo i valori dei parametri e delle grandezze elettriche alla risonanza del circuito RLC in serie uno per uno.
Frequenza di risonanza
La frequenza alla quale si verifica la risonanza è chiamata come resonant frequency fr. Nella serie RLC la risonanza del circuito si verifica quando il termine immaginario di impedenza Z è zero, cioè il valore di$X_L - X_C$ dovrebbe essere uguale a zero.
$$\Rightarrow X_L = X_C$$
Sostituto $X_L = 2 \pi f L$ e $X_C = \frac{1}{2 \pi f C}$ nell'equazione precedente.
$$2 \pi f L = \frac{1}{2 \pi f C}$$
$$\Rightarrow f^2 = \frac{1}{(2 \pi)^2 L C}$$
$$\Rightarrow f = \frac{1}{(2 \pi) \sqrt{LC}}$$
quindi, il resonant frequency fr del circuito RLC serie è
$$f_r = \frac{1}{(2 \pi) \sqrt{LC}}$$
Dove, L è l'induttanza di un induttore e C è la capacità di un condensatore.
Il resonant frequency fr del circuito della serie RLC dipende solo dall'induttanza L e capacità C. Ma è indipendente dalla resistenzaR.
Impedenza
Abbiamo il file impedance Z del circuito di serie RLC come
$$Z = R + j(X_L - X_C)$$
Sostituto $X_L = X_C$ nell'equazione precedente.
$$Z = R + j(X_C - X_C)$$
$$\Rightarrow Z = R + j(0)$$
$$\Rightarrow Z = R$$
Alla risonanza, il impedance Z del circuito della serie RLC è uguale al valore della resistenza R, cioè Z = R.
Corrente che scorre attraverso il circuito
Sostituto $X_L - X_C = 0$ nell'equazione 1.
$$V = I[R + j(0)]$$
$$\Rightarrow V = IR$$
$$\Rightarrow I = \frac{V}{R}$$
Perciò, current che scorre attraverso il circuito RLC serie a risonanza è $\mathbf{\mathit{I = \frac{V}{R}}}$.
Alla risonanza, l'impedenza del circuito RLC in serie raggiunge il valore minimo. Quindi ilmaximum current scorre attraverso questo circuito in risonanza.
Tensione attraverso il resistore
La tensione attraverso il resistore è
$$V_R = IR$$
Sostituisci il valore di I nell'equazione precedente.
$$V_R = \lgroup \frac{V}{R} \rgroup R$$
$$\Rightarrow V_R = V$$
quindi, il voltage across resistor alla risonanza è VR = V.
Tensione attraverso l'induttore
La tensione attraverso l'induttore è
$$V_L = I(jX_L)$$
Sostituisci il valore di I nell'equazione precedente.
$$V_L = \lgroup \frac{V}{R} \rgroup (jX_L)$$
$$\Rightarrow V_L = j \lgroup \frac{X_L}{R} \rgroup V$$
$$\Rightarrow V_L = j QV$$
quindi, il voltage across inductor alla risonanza è $V_L = j QV$.
Così la magnitude di tensione attraverso l'induttore alla risonanza sarà
$$|V_L| = QV$$
Dove Q è il Quality factor e il suo valore è uguale a $\frac{X_L}{R}$
Tensione attraverso il condensatore
La tensione ai capi del condensatore è
$$V_C = I(-j X_C)$$
Sostituisci il valore di I nell'equazione precedente.
$$V_C = \lgroup \frac{V}{R} \rgroup (-j X_C)$$
$$\Rightarrow V_C = -j \lgroup \frac{X_C}{R} \rgroup V$$
$$\Rightarrow V_C = -jQV$$
quindi, il voltage across capacitor alla risonanza è $\mathbf{\mathit{V_C = -jQV}}$.
Così la magnitude di tensione attraverso il condensatore alla risonanza sarà
$$|V_C| = QV$$
Dove Q è il Quality factor e il suo valore è uguale a $\frac{X_{C}}{R}$
Note - Il circuito RLC di risonanza in serie è chiamato come voltage magnificationcircuito, perché l'ampiezza della tensione ai capi dell'induttore e del condensatore è uguale a Q volte la tensione di ingresso sinusoidale V .
Nel capitolo precedente, abbiamo discusso l'importanza della risonanza in serie. Ora, parliamo della risonanza parallela nei circuiti RLC.
Schema del circuito di risonanza parallela
Se la risonanza si verifica in un circuito RLC parallelo, viene chiamata come Parallel Resonance. Considera quanto segueparallel RLC circuit, che è rappresentato nel dominio dei fasori.
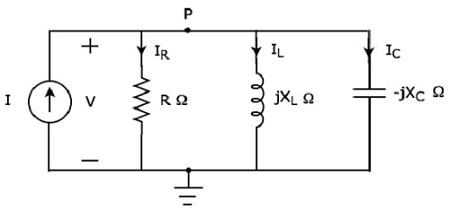
Qui, gli elementi passivi come resistenza, induttore e condensatore sono collegati in parallelo. Questa intera combinazione è dentroparallel con la sorgente di corrente sinusoidale in ingresso.
Scrivi nodal equation al nodo P.
$$- I + I_R + I_L + I_C = 0$$
$$\Rightarrow - I + \frac{V}{R} + \frac{V}{j X_L} + \frac{V}{-j X_C} = 0$$
$$\Rightarrow I = \frac{V}{R} - \frac{jV}{X_L} + \frac{jV}{X_C}$$
$\Rightarrow I = V[\frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup]$Equation 1
L'equazione di cui sopra ha la forma di I = VY.
quindi, il admittance Y del circuito RLC parallelo sarà
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$
Parametri e grandezze elettriche in risonanza
Ora, deriviamo i valori dei parametri e delle grandezze elettriche alla risonanza del circuito RLC parallelo uno per uno.
Frequenza di risonanza
Sappiamo che il file resonant frequency, frè la frequenza alla quale si verifica la risonanza. In parallelo si verifica la risonanza del circuito RLC, quando il termine immaginario di ammettenza, Y è zero. cioè il valore di$\frac{1}{X_C} - \frac{1}{X_L}$ dovrebbe essere uguale a zero
$$\Rightarrow \frac{1}{X_C} = \frac{1}{X_L}$$
$$\Rightarrow X_L = X_C$$
La condizione di risonanza sopra è uguale a quella del circuito RLC in serie. Così laresonant frequency, fr sarà lo stesso sia nel circuito RLC serie che nel circuito RLC parallelo.
quindi, il resonant frequency, fr del circuito RLC parallelo è
$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$
Dove,
- L è l'induttanza di un induttore.
- C è la capacità di un condensatore.
Il resonant frequency, fr del circuito RLC parallelo dipende solo dall'induttanza L e capacità C. Ma è indipendente dalla resistenzaR.
Ammissione
Abbiamo il file admittance Y del circuito RLC parallelo come
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$
Sostituto, $X_L = X_C$ nell'equazione precedente.
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_C} \rgroup$$
$$\Rightarrow Y = \frac{1}{R} + j(0)$$
$$\Rightarrow Y = \frac{1}{R}$$
Alla risonanza, il admittance, Y del circuito RLC parallelo è uguale al reciproco della resistenza, R. cioè, $\mathbf{\mathit{Y = \frac{1}{R}}}$
Tensione su ogni elemento
Sostituto, $\frac{1}{X_C} - \frac{1}{X_L} = 0$ nell'equazione 1
$$I = V [\frac{1}{R} + j(0)]$$
$$\Rightarrow I = \frac{V}{R}$$
$$\Rightarrow V = IR$$
quindi, il voltage attraverso tutti gli elementi del circuito RLC parallelo alla risonanza è V = IR.
Alla risonanza, l'ammettenza del circuito RLC parallelo raggiunge il valore minimo. Quindi,maximum voltage è presente in ogni elemento di questo circuito alla risonanza.
Corrente che scorre attraverso il resistore
La corrente che scorre attraverso il resistore è
$$I_R = \frac{V}{R}$$
Sostituisci il valore di V nell'equazione precedente.
$$I_R = \frac{IR}{R}$$
$$\Rightarrow I_R = I$$
quindi, il current flowing through resistor alla risonanza è $\mathbf{\mathit{I_R = I}}$.
Corrente che scorre attraverso l'induttore
La corrente che scorre attraverso l'induttore è
$$I_L = \frac{V}{j X_L}$$
Sostituisci il valore di V nell'equazione precedente.
$$I_L = \frac{IR}{j X_L}$$
$$\Rightarrow I_L = -j \lgroup \frac{R}{X_L} \rgroup I$$
$$\Rightarrow I_L = -jQI$$
quindi, il current flowing through inductor alla risonanza è $I_L = -jQI$.
Così la magnitude della corrente che fluisce attraverso l'induttore alla risonanza sarà
$$|I_L| = QI$$
Dove, Q è il file Quality factor e il suo valore è uguale a $\frac{R}{X_L}$
Corrente che scorre attraverso il condensatore
La corrente che scorre attraverso il condensatore è
$$I_C = \frac{V}{-j X_C}$$
Sostituisci il valore di V nell'equazione precedente.
$$I_C = \frac{IR}{-j X_C}$$
$$\Rightarrow I_C = j \lgroup \frac{R}{X_C} \rgroup I$$
$$\Rightarrow I_C = jQI$$
quindi, il current flowing through capacitor alla risonanza è $I_C = jQI$
Così la magnitude della corrente che fluisce attraverso il condensatore alla risonanza sarà
$$|I_C| = QI$$
Dove, Q è il file Quality factor e il suo valore è uguale a $\frac{R}{X_C}$
Note - Il circuito RLC a risonanza parallela è chiamato come current magnificationcircuito. Poiché, la grandezza della corrente che fluisce attraverso l'induttore e condensatore è uguale a Q volte la corrente di ingresso sinusoidale I .
Si dice che un circuito elettrico sia un coupled circuit, quando esiste una mutua induttanza tra le bobine (o induttori) presenti in quel circuito. La bobina non è altro che la combinazione in serie di resistore e induttore. In assenza di resistore, la bobina diventa induttore. A volte, i termini bobina e induttore sono usati in modo intercambiabile.
In questo capitolo, discuteremo prima della convenzione del punto e poi discuteremo della classificazione dell'accoppiamento.
Convenzione punto
La convenzione del punto è una tecnica che fornisce i dettagli sulla polarità della tensione al terminale tratteggiato. Questa informazione è utile durante la scrittura di equazioni KVL.
Se la corrente entra nel terminale tratteggiato di una bobina (o induttore), allora induce una tensione su un'altra bobina (o induttore), che sta avendo positive polarity al terminale tratteggiato.
Se la corrente parte dal terminale tratteggiato di una bobina (o induttore), allora induce una tensione su un'altra bobina (o induttore), che sta avendo negative polarity al terminale tratteggiato.
Classificazione dell'accoppiamento
Possiamo classificare coupling nelle seguenti due categorie.
- Accoppiamento elettrico
- Accoppiamento magnetico
Ora, parliamo di ogni tipo di accoppiamento uno per uno.
Accoppiamento elettrico
L'accoppiamento elettrico si verifica, quando esiste un physical connectiontra due bobine (o induttori). Questo accoppiamento può essere di tipo ausiliario o di tipo opposto. Si basa sul fatto che la corrente entri dal terminale tratteggiato o esca dal terminale tratteggiato.
Accoppiamento di tipo aiutante
Considera il seguente circuito elettrico, che ha due induttori collegati series.
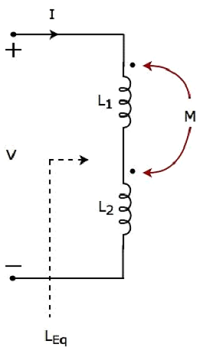
Poiché i due induttori sono collegati in serie, il same current Ifluiscono attraverso entrambi gli induttori aventi autoinduttanze L 1 e L 2 .
In questo caso, la corrente, la inserisco al terminale tratteggiato di ogni induttore. Quindi, la tensione indotta in ciascun induttore avràpositive polarity al terminale tratteggiato a causa della corrente che scorre in un'altra bobina.
Applicare KVL attorno al circuito del circuito o della rete elettrica di cui sopra.
$$V - L_1 \frac{dI}{dt} - M \frac{dI}{dt} - L_2 \frac{dI}{dt} - M \frac{dI}{dt} = 0$$
$$V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + 2M \frac{dI}{dt}$$
$$V = (L_1 + L_2 + 2M)\frac{dI}{dt}$$
L'equazione di cui sopra ha la forma di $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$
quindi, il equivalent inductance della combinazione in serie di induttori mostrati nella figura sopra è
$$L_{Eq} = L_1 + L_2 + 2M$$
In questo caso, l'induttanza equivalente è stata aumentata di 2M. Quindi, il circuito elettrico sopra è un esempio dielectrical accoppiamento che è di aiding genere.
Accoppiamento di tipo opposto
Considera il seguente circuito elettrico, che ha due induttori collegati series.
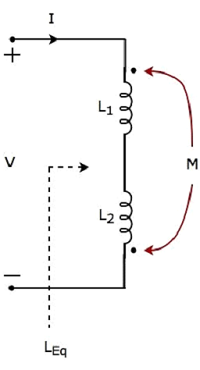
Nel circuito sopra, la corrente I entra nel terminale tratteggiato dell'induttore avente un'induttanza di L1. Quindi, induce una tensione nell'altro induttore avente un'induttanza diL2. Così,positive polarity della tensione indotta è presente al terminale tratteggiato di questo induttore.
Nel circuito sopra, la corrente I parte dal terminale tratteggiato dell'induttore avente un'induttanza di L2. Quindi, induce una tensione nell'altro induttore avente un'induttanza diL1. Così,negative polarity della tensione indotta è presente al terminale tratteggiato di questo induttore.
Applicare KVL attorno al circuito del circuito o della rete elettrica di cui sopra.
$$V - L_1 \frac{dI}{dt} + M \frac{dI}{dt} - L_2 \frac{dI}{dt} + M \frac{dI}{dt} = 0$$
$$\Rightarrow V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} - 2M \frac{dI}{dt}$$
$$\Rightarrow V = (L_1 + L_2 - 2M)\frac{dI}{dt}$$
L'equazione di cui sopra ha la forma di $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$
quindi, il equivalent inductance della combinazione in serie di induttori mostrati nella figura sopra è
$$L_{Eq} = L_1 + L_2 - 2M$$
In questo caso, l'induttanza equivalente è stata ridotta di 2M. Quindi, il circuito elettrico sopra è un esempio dielectrical accoppiamento che è di opposing genere.
Accoppiamento magnetico
L'accoppiamento magnetico si verifica, quando c'è no physical connectiontra due bobine (o induttori). Questo accoppiamento può essere di tipo ausiliario o di tipo opposto. Si basa sul fatto che la corrente entri dal terminale tratteggiato o esca dal terminale tratteggiato.
Accoppiamento di tipo aiutante
Considerare il seguente equivalente elettrico circuit of transformer. Ha due bobine e queste sono chiamate bobine primarie e secondarie.
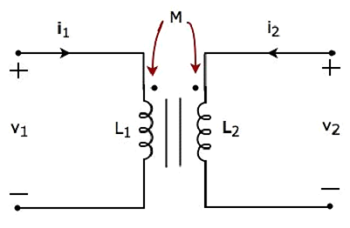
Le correnti che fluiscono attraverso le bobine primaria e secondaria sono rispettivamente i 1 e i 2 . In questo caso, queste correntienteral terminale tratteggiato della rispettiva bobina. Quindi, la tensione indotta in ciascuna bobina avrà polarità positiva al terminale tratteggiato a causa della corrente che scorre in un'altra bobina.
Applicare KVL attorno alla bobina primaria.
$$v_1 - L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt} = 0$$
$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt}$Equation 1
Applicare KVL attorno alla bobina secondaria.
$$v_2 - L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt} = 0$$
$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt}$Equation 2
Nell'equazione 1 e nell'equazione 2, la tensione autoindotta e la tensione mutuamente indotta hanno la stessa polarità. Quindi, il circuito del trasformatore sopra è un esempio dimagnetic coupling, che è di aiding genere.
Accoppiamento di tipo opposto
Considerare il seguente equivalente elettrico circuit of transformer.

Le correnti che fluiscono attraverso le bobine primaria e secondaria sono rispettivamente i 1 e i 2 . In questo caso, la corrente, i 1 entra nel terminale tratteggiato della bobina primaria. Quindi, induce una tensione nella bobina secondaria. Così,positive polarity della tensione indotta è presente al terminale tratteggiato di questa bobina secondaria.
Nel circuito sopra, la corrente, i 2 parte dal terminale tratteggiato della bobina secondaria. Quindi, induce una tensione nella bobina primaria. Così,negative polarity della tensione indotta è presente al terminale tratteggiato di questa bobina primaria.
Applicare KVL attorno alla bobina primaria.
$$v_1 - L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt} = 0$$
$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt}$Equation 3
Applicare KVL attorno alla bobina secondaria.
$$v_2 - L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt} = 0$$
$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt}$Equation 4
Nell'equazione 3 e nell'equazione 4, la tensione autoindotta e la tensione mutuamente indotta hanno polarità opposta. Quindi, il circuito del trasformatore sopra è un esempio dimagnetic coupling, che è di opposing genere.
In generale, è facile analizzare qualsiasi rete elettrica, se rappresentata con un modello equivalente, che fornisce la relazione tra le variabili di ingresso e di uscita. Per questo, possiamo usaretwo port networkrappresentazioni. Come suggerisce il nome, due port network contengono due porte. Tra queste, una porta viene utilizzata come porta di input e l'altra porta viene utilizzata come porta di output. La prima e la seconda porta sono chiamate rispettivamente port1 e port2.
One port networkè una rete elettrica a due terminali in cui la corrente entra da un terminale e esce da un altro terminale. Resistori, induttori e condensatori sono gli esempi di una rete di porte perché ognuno ha due terminali. Una rappresentazione della Port Network è mostrata nella figura seguente.
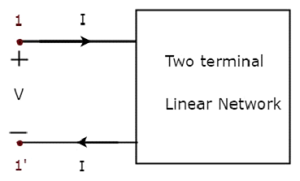
Qui, la coppia di terminali, 1 e 1 'rappresenta una porta. In questo caso, abbiamo solo una porta poiché è una rete a una porta.
Allo stesso modo, two port networkè una coppia di due terminali di rete elettrica in cui la corrente entra da un terminale ed esce da un altro terminale di ciascuna porta. La rappresentazione della rete a due porte è mostrata nella figura seguente.
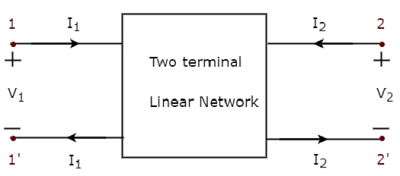
Qui, una coppia di terminali, 1 e 1 'rappresenta una porta, chiamata port1 e l'altra coppia di terminali, 2 e 2 'rappresenta un'altra porta, chiamata come port2.
Ci sono four variablesV 1 , V 2 , I 1 e I 2 in una rete a due porte come mostrato in figura. Da cui, possiamo scegliere due variabili come indipendenti e altre due variabili come dipendenti. Quindi, otterremo sei possibili coppie di equazioni. Queste equazioni rappresentano le variabili dipendenti in termini di variabili indipendenti. I coefficienti delle variabili indipendenti sono chiamati comeparameters. Quindi, ogni coppia di equazioni darà un insieme di quattro parametri.
Parametri di rete a due porte
I parametri di una rete a due porte sono chiamati come two port network parameterso semplicemente, due parametri di porta. Di seguito sono riportati i tipi di due parametri di Port Network.
- Parametri Z.
- Parametri Y.
- Parametri T.
- Parametri T '
- h-parameters
- g-parameters
Ora, parliamo di questi due parametri di port network uno per uno.
Parametri Z.
Otterremo il seguente insieme di due equazioni considerando le variabili V 1 & V 2 come dipendenti e I 1 & I 2 come indipendenti. I coefficienti delle variabili indipendenti, I 1 e I 2 sono chiamati comeZ parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Il Z parameters siamo
$$Z_{11} = \frac{V_1}{I_1}, \: when \: I_2 = 0$$
$$Z_{12} = \frac{V_1}{I_2}, \: when \: I_1 = 0$$
$$Z_{21} = \frac{V_2}{I_1}, \: when \: I_2 = 0$$
$$Z_{22} = \frac{V_2}{I_2}, \: when \: I_1 = 0$$
I parametri Z sono chiamati come impedance parametersperché questi sono semplicemente i rapporti di tensioni e correnti. Le unità dei parametri Z sono Ohm (Ω).
Possiamo calcolare due parametri Z, Z 11 e Z 21 , aprendo il circuito di port2. Allo stesso modo, possiamo calcolare gli altri due parametri Z, Z 12 e Z 22, aprendo il circuito di port1. Quindi, i parametri Z sono anche chiamati comeopen-circuit impedance parameters.
Parametri Y.
Otterremo il seguente insieme di due equazioni considerando le variabili I 1 & I 2 come dipendenti e V 1 & V 2 come indipendenti. I coefficienti delle variabili indipendenti, V 1 e V 2 sono chiamati comeY parameters.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
Il Y parameters siamo
$$Y_{11} = \frac{I_1}{V_1}, \: when \: V_2 = 0$$
$$Y_{12} = \frac{I_1}{V_2}, \: when \: V_1 = 0$$
$$Y_{21} = \frac{I_2}{V_1}, \: when \: V_2 = 0$$
$$Y_{22} = \frac{I_2}{V_2}, \: when \: V_1 = 0$$
I parametri Y sono chiamati come admittance parametersperché questi sono semplicemente i rapporti di correnti e tensioni. Le unità dei parametri Y sono mho.
Possiamo calcolare due parametri Y, Y 11 e Y 21, cortocircuitando la porta 2. Allo stesso modo, possiamo calcolare gli altri due parametri Y, Y 12 e Y 22, cortocircuitando la porta 1. Quindi, i parametri Y sono anche chiamati comeshort-circuit admittance parameters.
Parametri T.
Otterremo il seguente insieme di due equazioni considerando le variabili V 1 & I 1 come dipendenti e V 2 & I 2 come indipendenti. I coefficienti di V 2 e -I 2 sono chiamati comeT parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
Il T parameters siamo
$$A = \frac{V_1}{V_2}, \: when \: I_2 = 0$$
$$B = -\frac{V_1}{I_2}, \: when \: V_2 = 0$$
$$C = \frac{I_1}{V_2}, \: when \: I_2 = 0$$
$$D = -\frac{I_1}{I_2}, \: when \: V_2 = 0$$
I parametri T sono chiamati come parametri di trasmissione o ABCD parameters. I parametri, A e D non hanno unità, poiché sono di dimensioni inferiori. Le unità dei parametri, B e C sono rispettivamente ohm e mho.
Possiamo calcolare due parametri, A e C, aprendo il circuito di port2. Allo stesso modo, possiamo calcolare gli altri due parametri, B e D, cortocircuitando la porta2.
Parametri T '
Otterremo il seguente insieme di due equazioni considerando le variabili V 2 & I 2 come dipendenti e V 1 & I 1 come indipendenti. I coefficienti di V 1 e -I 1 sono chiamati comeT’ parameters.
$$V_2 = A' V_1 - B' I_1$$
$$I_2 = C' V_1 - D' I_1$$
Il T’ parameters siamo
$$A' = \frac{V_2}{V_1}, \: when\: I_1 = 0$$
$$B' = -\frac{V_2}{I_1}, \: when\: V_1 = 0$$
$$C' = \frac{I_2}{V_1}, \: when\: I_1 = 0$$
$$D' = -\frac{I_2}{I_1}, \: when \: V_1 = 0$$
I parametri T 'sono chiamati come parametri di trasmissione inversa o A’B’C’D’ parameters. I parametri A 'e D' non hanno unità, poiché sono meno dimensionali. Le unità dei parametri, B 'e C', sono rispettivamente Ohm e Mho.
Possiamo calcolare due parametri, A 'e C', facendo un circuito aperto di port1. Allo stesso modo, possiamo calcolare gli altri due parametri, B 'e D', eseguendo un cortocircuito su port1.
parametri h
Otterremo il seguente insieme di due equazioni considerando le variabili V 1 & I 2 come dipendenti e I 1 & V 2 come indipendenti. I coefficienti delle variabili indipendenti, I 1 e V 2 , sono chiamati comeh-parameters.
$$V_1 = h_{11} I_1 + h_{12} V_2$$
$$I_2 = h_{21} I_1 + h_{22} V_2$$
I parametri h sono
$$h_{11} = \frac{V_1}{I_1},\: when\: V_2 = 0$$
$$h_{12} = \frac{V_1}{V_2},\: when\: I_1 = 0$$
$$h_{21} = \frac{I_2}{I_1},\: when\: V_2 = 0$$
$$h_{22} = \frac{I_2}{V_2},\: when\: I_1 = 0$$
I parametri h sono chiamati come hybrid parameters. I parametri, h 12 e h 21 , non hanno unità, poiché sono privi di dimensione. Le unità dei parametri, h 11 e h 22 , sono rispettivamente Ohm e Mho.
Possiamo calcolare due parametri, h 11 e h 21 facendo cortocircuito di port2. Allo stesso modo, possiamo calcolare gli altri due parametri, h 12 e h 22, aprendo il circuito di port1.
I parametri h oi parametri ibridi sono utili nei circuiti di modellazione dei transistor (reti).
parametri g
Otterremo il seguente insieme di due equazioni considerando le variabili I 1 & V 2 come dipendenti e V 1 & I 2 come indipendenti. I coefficienti delle variabili indipendenti, V 1 e I 2 sono chiamati comeg-parameters.
$$I_1 = g_{11} V_1 + g_{12} I_2$$
$$V_2 = g_{21} V_1 + g_{22} I_2$$
Il g-parameters siamo
$$g_{11} = \frac{I_1}{V_1},\: when\: I_2 = 0$$
$$g_{12} = \frac{I_1}{I_2},\: when\: V_1 = 0$$
$$g_{21} = \frac{V_2}{V_1},\: when\: I_2 = 0$$
$$g_{22} = \frac{V_2}{I_2},\: when \: V_1 = 0$$
I parametri g sono chiamati come inverse hybrid parameters. I parametri, g 12 e g 21 non hanno unità, poiché sono di dimensione inferiore. Le unità dei parametri, g 11 e g 22 sono rispettivamente mho e ohm.
Possiamo calcolare due parametri, g 11 eg 21, aprendo il circuito di port2. Allo stesso modo, possiamo calcolare gli altri due parametri, g 12 e g 22, cortocircuitando la porta 1.
Nel capitolo precedente, abbiamo discusso di sei tipi di parametri di rete a due porte. Ora, convertiamo un set di parametri di rete a due porte in un altro set di parametri di rete a due porte. Questa conversione è nota come conversione dei parametri di rete a due porte o semplicemente,two-port parameters conversion.
A volte, è facile trovare facilmente un insieme di parametri di una data rete elettrica. In queste situazioni, possiamo convertire questi parametri nel set di parametri richiesto invece di calcolare questi parametri direttamente con maggiore difficoltà.
Ora, discutiamo di alcune delle due conversioni dei parametri di porta.
Procedura di conversione di due parametri di porta
Seguire questi passaggi, mentre si converte un set di due parametri di Port Network nell'altro set di due parametri di Port Network.
Step 1 - Scrivere le equazioni di una rete a due porte in termini di parametri desiderati.
Step 2 - Scrivere le equazioni di una rete a due porte in termini di parametri dati.
Step 3 - Riorganizzare le equazioni di Step2 in modo che siano simili alle equazioni di Step1.
Step 4- Uguagliando le simili equazioni di Step1 e Step3, otterremo i parametri desiderati in termini di parametri dati. Possiamo rappresentare questi parametri in forma di matrice.
Da parametri Z a parametri Y.
Qui dobbiamo rappresentare i parametri Y in termini di parametri Z. Quindi, in questo caso i parametri Y sono i parametri desiderati e i parametri Z sono i parametri dati.
Step 1 - Sappiamo che il seguente insieme di due equazioni, che rappresenta una rete a due porte in termini di Y parameters.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
Possiamo rappresentare le due equazioni precedenti in matrix forma come
$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 1
Step 2 - Sappiamo che il seguente insieme di due equazioni, che rappresenta una rete a due porte in termini di Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Possiamo rappresentare le due equazioni precedenti in matrix forma come
$$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$$
Step 3 - Possiamo modificarlo come
$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 2
Step 4 - Uguagliando l'equazione 1 e l'equazione 2, otterremo
$$\begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} $$
$$\Rightarrow \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \frac{\begin{bmatrix}Z_{22} & -Z_{12} \\-Z_{21} & Z_{11} \end{bmatrix}}{\Delta Z}$$
Dove,
$$\Delta Z = Z_{11} Z_{22} - Z_{12} Z_{21}$$
Quindi, semplicemente eseguendo il file inverse of Z parameters matrix, otterremo la matrice dei parametri Y.
Da parametri Z a parametri T.
Qui dobbiamo rappresentare i parametri T in termini di parametri Z. Quindi, in questo caso i parametri T sono i parametri desiderati e i parametri Z sono i parametri dati.
Step 1 - Sappiamo che, il seguente insieme di due equazioni, che rappresenta una rete a due porte in termini di T parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
Step 2 - Sappiamo che il seguente insieme di due equazioni, che rappresenta una rete a due porte in termini di Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Step 3 - Possiamo modificare l'equazione di cui sopra come
$$\Rightarrow V_2 - Z_{22} I_2 = Z_{21} I_1$$
$$\Rightarrow I_1 = \lgroup \frac{1}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{22}}{Z_{21}} \rgroup I_2$$
Step 4 - L'equazione di cui sopra ha la forma di $I_1 = CV_2 − DI_2$. Qui,
$$C = \frac{1}{Z_{21}}$$
$$D = \frac{Z_{22}}{Z_{21}}$$
Step 5 - Sostituto $I_1$ valore del passaggio 3 in $V_1$ equazione del passaggio 2.
$$V_1 = Z_{11} \lbrace \lgroup \frac {1}{Z_{12}} \rgroup V_2 - \lgroup \frac {Z_{22}}{Z_{21}} \rgroup I_2 \rbrace + Z_{12} I_2$$
$$\Rightarrow V_1 = \lgroup \frac {Z_{11}}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}} \rgroup I_2$$
Step 6 - L'equazione di cui sopra ha la forma di $V_1 = AV_2 − BI_2$. Qui,
$$A = \frac{Z_{11}}{Z_{21}}$$
$$B = \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}}$$
Step 7 - Pertanto, il file T parameters matrix è
$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{Z_{11}}{Z_{21}} & \frac{Z_{11}Z_{22} - Z_{12}Z_{21}}{Z_{21}} \\\frac{1}{Z_{21}} & \frac{Z_{22}}{Z_{21}} \end{bmatrix}$$
Parametri Y ai parametri Z.
Qui dobbiamo rappresentare i parametri Z in termini di parametri Y. Quindi, in questo caso i parametri Z sono i parametri desiderati e i parametri Y sono i parametri dati.
Step 1 - Sappiamo che, la seguente equazione di matrice di due port network per quanto riguarda i parametri Z come
$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 3
Step 2 - Sappiamo che, la seguente equazione di matrice di due port network per quanto riguarda i parametri Y come
$$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$$
Step 3 - Possiamo modificarlo come
$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 4
Step 4 - Uguagliando l'equazione 3 e l'equazione 4, otterremo
$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1}$$
$$\Rightarrow \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \frac{\begin{bmatrix}Y_{22} & - Y_{12} \\- Y_{21} & Y_{11} \end{bmatrix}}{\Delta Y}$$
Dove,
$$\Delta Y = Y_{11} Y_{22} - Y_{12} Y_{21}$$
Quindi, semplicemente eseguendo il file inverse of Y parameters matrix, otterremo la matrice dei parametri Z.
Parametri Y ai parametri T.
Qui, dobbiamo rappresentare i parametri T in termini di parametri Y. Quindi, in questo caso, i parametri T sono i parametri desiderati e i parametri Y sono i parametri dati.
Step 1 - Sappiamo che, il seguente insieme di due equazioni, che rappresenta una rete a due porte in termini di T parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
Step 2 - Sappiamo che il seguente insieme di due equazioni di due port network riguardanti i parametri Y.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
Step 3 - Possiamo modificare l'equazione di cui sopra come
$$\Rightarrow I_2 - Y_{22} V_2 = Y_{21} V_1$$
$$\Rightarrow V_1 = \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2$$
Step 4 - L'equazione di cui sopra ha la forma di $V_1 = AV_2 − BI_2$. Qui,
$$A = \frac{- Y_{22}}{Y_{21}}$$
$$B = \frac{-1}{Y_{21}}$$
Step 5 - Sostituto $V_1$ valore del passaggio 3 in $I_1$ equazione del passaggio 2.
$$I_1 = Y_{11} \lbrace \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2 \rbrace + Y_{12} V_2$$
$$\Rightarrow I_1 = \lgroup \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{- Y_{11}} {Y_{21}} \rgroup I_2$$
Step 6 - L'equazione di cui sopra ha la forma di $I_1 = CV_2 − DI_2$. Qui,
$$C = \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}}$$
$$D = \frac{- Y_{11}} {Y_{21}}$$
Step 7 - Pertanto, il file T parameters matrix è
$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{-Y_{22}}{Y_{21}} & \frac{-1}{Y_{21}} \\\frac{Y_{12}Y_{21} - Y_{11}Y_{22}}{Y_{21}} & \frac{-Y_{11}}{Y_{21}} \end{bmatrix}$$
Da parametri T a parametri h
Qui, dobbiamo rappresentare i parametri h in termini di parametri T. Quindi, in questo caso hparameters sono i parametri desiderati e parametri T sono i parametri dati.
Step 1 - Lo sappiamo, quanto segue h-parameters di una rete a due porte.
$$h_{11} = \frac{V_1}{I_1}, \: when \: V_2 = 0$$
$$h_{12} = \frac{V_1}{V_2}, \: when \: I_1 = 0$$
$$h_{21} = \frac{I_2}{I_1}, \: when \: V_2 = 0$$
$$h_{22} = \frac{I_2}{V_2}, \: when \: I_1 = 0$$
Step 2 - Sappiamo che il seguente insieme di due equazioni di due port network per quanto riguarda T parameters.
$V_1 = A V_2 - B I_2$Equation 5
$I_1 = C V_2 - D I_2$Equation 6
Step 3 - Sostituto $V_2 = 0$ nelle equazioni precedenti per trovare i due parametri h, $h_{11}$ e $h_{21}$.
$$\Rightarrow V_1 = -B I_2$$
$$\Rightarrow I_1 = -D I_2$$
Sostituto, $V_1$ e $I_1$ valori nel parametro h, $h_{11}$.
$$h_{11} = \frac{-B I_2}{-D I_2}$$
$$\Rightarrow h_{11} = \frac{B}{D}$$
Sostituto $I_1$ valore nel parametro h $h_{21}$.
$$h_{21} = \frac{I_2}{- D I_2}$$
$$\Rightarrow h_{21} = - \frac{1}{D}$$
Step 4 - Sostituto $I_1 = 0$ nella seconda equazione del passaggio 2 per trovare il parametro h $h_{22}$.
$$0 = C V_2 - D I_2$$
$$\Rightarrow C V_2 = D I_2$$
$$\Rightarrow \frac{I_2}{V_2} = \frac{C}{D}$$
$$\Rightarrow h_{22} = \frac{C}{D}$$
Step 5 - Sostituto $I_2 = \lgroup \frac{C}{D} \rgroup V_2$ nella prima equazione del passaggio 2 per trovare il parametro h, $h_{12}$.
$$V_1 = A V_2 - B \lgroup \frac{C}{D} \rgroup V_2$$
$$\Rightarrow V_1 = \lgroup \frac{AD - BC}{D} \rgroup V_2$$
$$\Rightarrow \frac{V_1}{V_2} = \frac{AD - BC}{D}$$
$$\Rightarrow h_{12} = \frac{AD - BC}{D}$$
Step 6 - Pertanto, la matrice dei parametri h è
$$\begin{bmatrix}h_{11} & h_{12} \\h_{21} & h_{22} \end{bmatrix} = \begin{bmatrix}\frac{B}{D} & \frac{AD - BC}{D} \\-\frac{1}{D} & \frac{C}{D} \end{bmatrix}$$
parametri h ai parametri Z.
Qui dobbiamo rappresentare i parametri Z in termini di parametri h. Quindi, in questo caso i parametri Z sono i parametri desiderati e i parametri h sono i parametri dati.
Step 1 - Sappiamo che, il seguente insieme di due equazioni di due port network per quanto riguarda Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Step 2 - Sappiamo che, il seguente insieme di due equazioni di rete a due porte per quanto riguarda h-parameters.
$$V_1 = h_{11} I_1 + h_{12} V_2$$
$$I_2 = h_{21} I_1 + h_{22} V_2$$
Step 3 - Possiamo modificare l'equazione di cui sopra come
$$\Rightarrow I_2 - h_{21} I_1 = h_{22} V_2$$
$$\Rightarrow V_2 = \frac{I_2 - h_{21} I_1}{h_{22}}$$
$$\Rightarrow V_2 = \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2$$
L'equazione di cui sopra ha la forma di $V_2 = Z_{21} I_1 + Z_{22} I_2. Here,$
$$Z_{21} = \frac{-h_{21}}{h_{22}}$$
$$Z_{22} = \frac{1}{h_{22}}$$
Step 4- Sostituire il valore V 2 nella prima equazione del passaggio 2.
$$V_1 = h_{11} I_1 + h_{21} \lbrace \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2 \rbrace$$
$$\Rightarrow V_1 = \lgroup \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{h_{12}}{h_{22}} \rgroup I_2$$
L'equazione di cui sopra ha la forma di $V_1 = Z_{11}I_1 + Z_{12}I_2$. Qui,
$$Z_{11} = \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}}$$
$$Z_{12} = \frac{h_{12}}{h_{22}}$$
Step 5 - Pertanto, la matrice dei parametri Z è
$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}\frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} & \frac{h_{12}}{h_{22}} \\\frac{-h_{21}}{h_{22}} & \frac{1}{h_{22}} \end{bmatrix}$$
In questo modo, possiamo convertire un insieme di parametri in un altro insieme di parametri.
Filtri come suggerisce il nome, filtrano i componenti della frequenza. Ciò significa che consentono determinati componenti di frequenza e / o rifiutano altri componenti di frequenza.
In questo capitolo, parliamo di passive filters. Questi sono i circuiti elettrici o le reti che hanno elementi passivi come resistore, induttore e condensatore.
Tipi di filtri
I filtri sono principalmente classificati in four typesin base alla banda di frequenze consentite e / o alla banda di frequenze rifiutate. Di seguito sono riportati i tipi di filtri.
- Filtro passa basso
- Filtro passa alto
- Filtro passa banda
- Filtro Band Stop
Filtro passa basso
Filtro passa basso come suggerisce il nome, consente solo (passa) low frequencycomponenti. Ciò significa che rifiuta (blocca) tutti gli altri componenti ad alta frequenza.
Il dominio s circuit diagram (rete) del filtro passa basso è mostrato nella figura seguente.
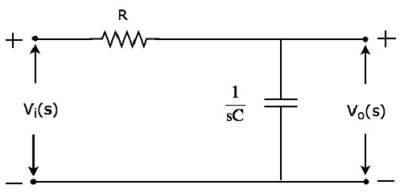
Consiste di due elementi passivi resistore e condensatore, che sono collegati in series. La tensione di ingresso viene applicata all'intera combinazione e l'uscita è considerata come la tensione ai capi del condensatore.
Qui, $V_i(s)$ e $V_o(s)$ sono le trasformate di Laplace della tensione di ingresso, $v_i(t)$ e tensione di uscita, $v_o(t)$ rispettivamente.
Il transfer function della rete di cui sopra è
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{\frac{1}{sC}}{R + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{1}{1 + sCR}$$
Sostituto, $s = j \omega$ nell'equazione precedente.
$$H(j \omega) = \frac{1}{1 + j \omega CR}$$
L'entità della funzione di trasferimento è
$$|H(j \omega)| = \frac{1}{\sqrt{(1 + (\omega CR)^2}}$$
A ω = 0, l'ampiezza della funzione di trasferimento è uguale a 1.
A $\omega = \frac{1}{CR}$, l'ampiezza della funzione di trasferimento è pari a 0,707.
A ω = ∞, l'ampiezza della funzione di trasferimento è uguale a 0.
Pertanto, l'entità della funzione di trasferimento di Low pass filtervarierà da 1 a 0 poiché ω varia da 0 a ∞.
Filtro passa alto
Filtro passa alto come suggerisce il nome, consente solo (passa) high frequencycomponenti. Ciò significa che rifiuta (blocca) tutti i componenti a bassa frequenza.
Il dominio s circuit diagram (rete) del filtro passa-alto è mostrato nella figura seguente.
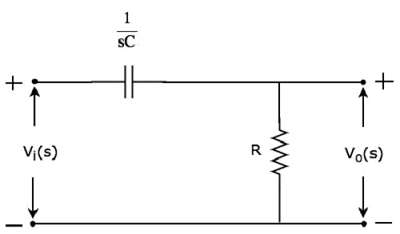
Consiste di due elementi passivi condensatore e resistore, che sono collegati in series. La tensione di ingresso viene applicata a tutta questa combinazione e l'uscita è considerata come la tensione attraverso il resistore.
Qui, $V_i(s)$ e $V_o(s)$ sono le trasformate di Laplace della tensione di ingresso, $v_i(t)$ e tensione di uscita, $v_o(t)$ rispettivamente.
Il transfer function della rete di cui sopra è
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{sCR}{1 + sCR}$$
Sostituto, $s = j \omega$ nell'equazione precedente.
$$H(j \omega) = \frac{j \omega CR}{1 + j \omega CR}$$
L'entità della funzione di trasferimento è
$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 + (\omega CR)^2}}$$
A ω = 0, l'ampiezza della funzione di trasferimento è uguale a 0.
A $\omega = \frac{1}{CR}$, l'ampiezza della funzione di trasferimento è pari a 0,707.
A ω = ∞, l'ampiezza della funzione di trasferimento è uguale a 1.
Pertanto, l'entità della funzione di trasferimento di High pass filtervarierà da 0 a 1 poiché ω varia da 0 a ∞.
Filtro passa banda
Filtro passa banda come suggerisce il nome, esso allows (passa) solo one banddelle frequenze. In generale, questa banda di frequenza si trova tra la gamma delle basse frequenze e la gamma delle alte frequenze. Ciò significa che questo filtro rifiuta (blocca) sia i componenti a bassa che ad alta frequenza.
Il dominio s circuit diagram (rete) del filtro passa banda è mostrato nella figura seguente.
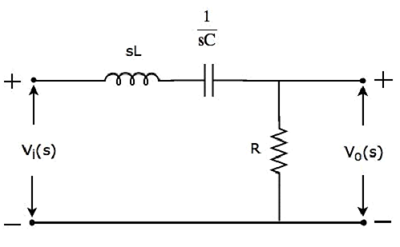
Consiste di tre elementi passivi induttore, condensatore e resistore, che sono collegati in series. La tensione di ingresso viene applicata a tutta questa combinazione e l'uscita è considerata come la tensione attraverso il resistore.
Qui, $V_i(s)$ e $V_o(s)$ sono le trasformate di Laplace della tensione di ingresso, $v_i(t)$ e tensione di uscita, $v_o(t)$ rispettivamente.
Il transfer function della rete di cui sopra è
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC} + sL}$$
$$\Rightarrow H(s) = \frac{s CR}{s^2 LC + sCR + 1}$$
Sostituto $s = j \omega$ nell'equazione precedente.
$$H(j \omega) = \frac{j \omega CR}{1 - \omega^2 LC + j \omega CR}$$
L'entità della funzione di trasferimento è
$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$
A ω = 0, l'ampiezza della funzione di trasferimento è uguale a 0.
A $\omega = \frac{1}{\sqrt{LC}}$, l'ampiezza della funzione di trasferimento è uguale a 1.
A ω = ∞, l'ampiezza della funzione di trasferimento è uguale a 0.
Pertanto, l'entità della funzione di trasferimento di Band pass filtervarierà da 0 a 1 e da 1 a 0 poiché ω varia da 0 a ∞.
Filtro Band Stop
Filtro Band Stop come suggerisce il nome, rifiuta (blocca) solo una banda di frequenze. In generale, questa banda di frequenza si trova tra la gamma delle basse frequenze e la gamma delle alte frequenze. Ciò significa che questo filtro consente (passa) componenti sia a bassa che ad alta frequenza.
Il dominio s (rete) di circuit diagrame il filtro di arresto è mostrato nella figura seguente.
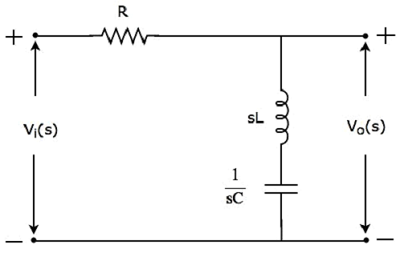
Consiste di tre elementi passivi resistore, induttore e condensatore, che sono collegati in series. La tensione di ingresso viene applicata a tutta questa combinazione e l'uscita è considerata come la tensione attraverso la combinazione di induttore e condensatore.
Qui, $V_i(s)$ e $V_o(s)$ sono le trasformate di Laplace della tensione di ingresso, $v_i(t)$ e tensione di uscita, $v_o(t)$ rispettivamente.
Il transfer function della rete di cui sopra è
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{sL + \frac{1}{sC}}{R + sL + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{s^2 LC + 1}{s^2 LC + sCR + 1}$$
Sostituto, $s = j \omega$ nell'equazione precedente.
$$H(j \omega) = \frac{1 - \omega^2 LC}{1 - \omega^2 LC + j \omega CR}$$
L'entità della funzione di trasferimento è
$$|H(j \omega)| = \frac{1 - \omega^2 LC}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$
A ω = 0, l'ampiezza della funzione di trasferimento è uguale a 1.
A $\omega = \frac{1}{\sqrt{LC}}$, l'ampiezza della funzione di trasferimento è uguale a 0.
A ω = ∞, l'ampiezza della funzione di trasferimento è uguale a 1.
Pertanto, l'entità della funzione di trasferimento di Band stop filtervarierà da 1 a 0 e da 0 a 1 poiché ω varia da 0 a ∞.