SciPy - Guida rapida
SciPy, pronunciato come Sigh Pi, è un python scientifico open source, distribuito sotto la libreria con licenza BSD per eseguire calcoli matematici, scientifici e ingegneristici.
La libreria SciPy dipende da NumPy, che fornisce una manipolazione di array N-dimensionale comoda e veloce. La libreria SciPy è costruita per funzionare con gli array NumPy e fornisce molte pratiche numeriche facili da usare ed efficienti come routine per l'integrazione e l'ottimizzazione numerica. Insieme, funzionano su tutti i sistemi operativi più diffusi, sono veloci da installare e sono gratuiti. NumPy e SciPy sono facili da usare, ma abbastanza potenti da poter dipendere da alcuni dei principali scienziati e ingegneri del mondo.
Pacchetti secondari SciPy
SciPy è organizzato in sotto-pacchetti che coprono diversi domini di calcolo scientifico. Questi sono riassunti nella tabella seguente:
| scipy.cluster | Quantizzazione vettoriale / Kmeans |
| scipy.constants | Costanti fisiche e matematiche |
| scipy.fftpack | trasformata di Fourier |
| scipy.integrate | Routine di integrazione |
| scipy.interpolate | Interpolazione |
| scipy.io | Input e output dei dati |
| scipy.linalg | Routine di algebra lineare |
| scipy.ndimage | Pacchetto di immagini n-dimensionali |
| scipy.odr | Regressione ortogonale della distanza |
| scipy.optimize | Ottimizzazione |
| scipy.signal | Elaborazione del segnale |
| scipy.sparse | Matrici sparse |
| scipy.spatial | Strutture e algoritmi di dati spaziali |
| scipy.special | Eventuali funzioni matematiche speciali |
| scipy.stats | Statistiche |
Struttura dati
La struttura dati di base utilizzata da SciPy è un array multidimensionale fornito dal modulo NumPy. NumPy fornisce alcune funzioni per l'algebra lineare, le trasformate di Fourier e la generazione di numeri casuali, ma non con la generalità delle funzioni equivalenti in SciPy.
La distribuzione standard di Python non viene fornita in bundle con alcun modulo SciPy. Un'alternativa leggera è installare SciPy utilizzando il popolare programma di installazione del pacchetto Python,
pip install pandasSe installiamo il file Anaconda Python package, Pandas verrà installato per impostazione predefinita. Di seguito sono riportati i pacchetti e i collegamenti per installarli in diversi sistemi operativi.
finestre
Anaconda (a partire dal https://www.continuum.io) è una distribuzione Python gratuita per lo stack SciPy. È disponibile anche per Linux e Mac.
Canopy (https://www.enthought.com/products/canopy/) è disponibile gratuitamente, così come per la distribuzione commerciale con uno stack SciPy completo per Windows, Linux e Mac.
Python (x,y)- È una distribuzione Python gratuita con stack SciPy e Spyder IDE per il sistema operativo Windows. (Scaricabile dahttps://python-xy.github.io/)
Linux
I gestori di pacchetti delle rispettive distribuzioni Linux vengono utilizzati per installare uno o più pacchetti nello stack SciPy.
Ubuntu
Possiamo usare il seguente percorso per installare Python in Ubuntu.
sudo apt-get install python-numpy python-scipy
python-matplotlibipythonipython-notebook python-pandas python-sympy python-noseFedora
Possiamo usare il seguente percorso per installare Python in Fedora.
sudo yum install numpyscipy python-matplotlibipython python-pandas
sympy python-nose atlas-develPer impostazione predefinita, tutte le funzioni NumPy erano disponibili tramite lo spazio dei nomi SciPy. Non è necessario importare esplicitamente le funzioni NumPy, quando SciPy viene importato. L'oggetto principale di NumPy è l'array multidimensionale omogeneo. È una tabella di elementi (solitamente numeri), tutti dello stesso tipo, indicizzati da una tupla di interi positivi. In NumPy, le dimensioni sono chiamate assi. Il numero diaxes è chiamato come rank.
Ora, rivediamo le funzionalità di base di vettori e matrici in NumPy. Poiché SciPy è basato sugli array NumPy, è necessaria la comprensione delle basi di NumPy. Poiché la maggior parte delle parti dell'algebra lineare si occupa solo di matrici.
NumPy vettore
Un vettore può essere creato in diversi modi. Alcuni di loro sono descritti di seguito.
Conversione di oggetti simili ad array Python in NumPy
Consideriamo il seguente esempio.
import numpy as np
list = [1,2,3,4]
arr = np.array(list)
print arrL'output del programma di cui sopra sarà il seguente.
[1 2 3 4]Creazione intrinseca di array NumPy
NumPy ha funzioni integrate per creare array da zero. Alcune di queste funzioni sono spiegate di seguito.
Utilizzando zeri ()
La funzione zeri (forma) creerà un array riempito con 0 valori con la forma specificata. Il dtype predefinito è float64. Consideriamo il seguente esempio.
import numpy as np
print np.zeros((2, 3))L'output del programma di cui sopra sarà il seguente.
array([[ 0., 0., 0.],
[ 0., 0., 0.]])Usando quelli ()
La funzione ones (forma) creerà un array riempito con 1 valori. È identico agli zeri sotto tutti gli altri aspetti. Consideriamo il seguente esempio.
import numpy as np
print np.ones((2, 3))L'output del programma di cui sopra sarà il seguente.
array([[ 1., 1., 1.],
[ 1., 1., 1.]])Usare arange ()
La funzione arange () creerà array con valori che aumentano regolarmente. Consideriamo il seguente esempio.
import numpy as np
print np.arange(7)Il programma precedente genererà il seguente output.
array([0, 1, 2, 3, 4, 5, 6])Definizione del tipo di dati dei valori
Consideriamo il seguente esempio.
import numpy as np
arr = np.arange(2, 10, dtype = np.float)
print arr
print "Array Data Type :",arr.dtypeIl programma precedente genererà il seguente output.
[ 2. 3. 4. 5. 6. 7. 8. 9.]
Array Data Type : float64Usare linspace ()
La funzione linspace () creerà array con un numero specificato di elementi, che saranno equidistanti tra i valori di inizio e fine specificati. Consideriamo il seguente esempio.
import numpy as np
print np.linspace(1., 4., 6)Il programma precedente genererà il seguente output.
array([ 1. , 1.6, 2.2, 2.8, 3.4, 4. ])Matrice
Una matrice è un array 2-D specializzato che mantiene la sua natura 2-D attraverso le operazioni. Ha alcuni operatori speciali, come * (moltiplicazione della matrice) e ** (potenza della matrice). Consideriamo il seguente esempio.
import numpy as np
print np.matrix('1 2; 3 4')Il programma precedente genererà il seguente output.
matrix([[1, 2],
[3, 4]])Trasposizione coniugata di Matrix
Questa funzione restituisce la trasposizione coniugata (complessa) di self. Consideriamo il seguente esempio.
import numpy as np
mat = np.matrix('1 2; 3 4')
print mat.HIl programma precedente genererà il seguente output.
matrix([[1, 3],
[2, 4]])Trasposizione di Matrix
Questa caratteristica restituisce la trasposizione del sé. Consideriamo il seguente esempio.
import numpy as np
mat = np.matrix('1 2; 3 4')
mat.TIl programma precedente genererà il seguente output.
matrix([[1, 3],
[2, 4]])Quando trasponiamo una matrice, creiamo una nuova matrice le cui righe sono le colonne dell'originale. Una trasposizione coniugata, invece, scambia l'indice di riga e di colonna per ogni elemento della matrice. L'inverso di una matrice è una matrice che, se moltiplicata con la matrice originale, si traduce in una matrice identità.
K-means clusteringè un metodo per trovare cluster e centri di cluster in un set di dati senza etichetta. Intuitivamente, potremmo pensare a un cluster come - composto da un gruppo di punti dati, le cui distanze tra i punti sono piccole rispetto alle distanze dai punti esterni al cluster. Dato un insieme iniziale di centri K, l'algoritmo K-mean itera i seguenti due passaggi:
Per ogni centro, viene identificato il sottoinsieme di punti di formazione (il suo cluster) più vicino ad esso rispetto a qualsiasi altro centro.
Viene calcolata la media di ciascuna caratteristica per i punti dati in ogni cluster e questo vettore medio diventa il nuovo centro per quel cluster.
Questi due passaggi vengono ripetuti fino a quando i centri non si spostano più o le assegnazioni non cambiano più. Quindi, un nuovo puntoxpuò essere assegnato al cluster del prototipo più vicino. La libreria SciPy fornisce una buona implementazione dell'algoritmo K-Means attraverso il pacchetto cluster. Facci capire come usarlo.
Implementazione di K-Means in SciPy
Capiremo come implementare K-Means in SciPy.
Importa K-Means
Vedremo l'implementazione e l'utilizzo di ogni funzione importata.
from SciPy.cluster.vq import kmeans,vq,whitenGenerazione dei dati
Dobbiamo simulare alcuni dati per esplorare il clustering.
from numpy import vstack,array
from numpy.random import rand
# data generation with three features
data = vstack((rand(100,3) + array([.5,.5,.5]),rand(100,3)))Ora dobbiamo controllare i dati. Il programma precedente genererà il seguente output.
array([[ 1.48598868e+00, 8.17445796e-01, 1.00834051e+00],
[ 8.45299768e-01, 1.35450732e+00, 8.66323621e-01],
[ 1.27725864e+00, 1.00622682e+00, 8.43735610e-01],
…………….Normalizza un gruppo di osservazioni in base alle caratteristiche. Prima di eseguire K-Means, è utile riscalare ogni dimensione caratteristica del set di osservazione con lo sbiancamento. Ogni caratteristica è divisa per la sua deviazione standard in tutte le osservazioni per dargli una varianza unitaria.
Sbianca i dati
Dobbiamo usare il seguente codice per sbiancare i dati.
# whitening of data
data = whiten(data)Calcola le medie K con tre cluster
Calcoliamo ora K-Means con tre cluster utilizzando il codice seguente.
# computing K-Means with K = 3 (2 clusters)
centroids,_ = kmeans(data,3)Il codice sopra esegue K-Means su un insieme di vettori di osservazione che formano K cluster. L'algoritmo K-Means regola i centroidi fino a quando non è possibile ottenere un progresso sufficiente, ovvero il cambiamento nella distorsione, poiché l'ultima iterazione è inferiore a una certa soglia. Qui, possiamo osservare il centroide del cluster stampando la variabile centroidi utilizzando il codice fornito di seguito.
print(centroids)Il codice precedente genererà il seguente output.
print(centroids)[ [ 2.26034702 1.43924335 1.3697022 ]
[ 2.63788572 2.81446462 2.85163854]
[ 0.73507256 1.30801855 1.44477558] ]Assegna ogni valore a un cluster utilizzando il codice fornito di seguito.
# assign each sample to a cluster
clx,_ = vq(data,centroids)Il vq la funzione confronta ogni vettore di osservazione nella 'M' con 'N' obsarray con i centroidi e assegna l'osservazione al cluster più vicino. Restituisce il cluster di ogni osservazione e la distorsione. Possiamo controllare anche la distorsione. Controlliamo il cluster di ciascuna osservazione utilizzando il codice seguente.
# check clusters of observation
print clxIl codice precedente genererà il seguente output.
array([1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 2, 0, 2, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0,
0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0,
2, 2, 2, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)I valori distinti 0, 1, 2 della matrice precedente indicano i cluster.
Il pacchetto delle costanti SciPy fornisce un'ampia gamma di costanti, che vengono utilizzate nell'area scientifica generale.
Pacchetto costanti SciPy
Il scipy.constants packagefornisce varie costanti. Dobbiamo importare le costanti richieste e usarle secondo il requisito. Vediamo come queste variabili costanti vengono importate e utilizzate.
Per cominciare, confrontiamo il valore "pi" considerando il seguente esempio.
#Import pi constant from both the packages
from scipy.constants import pi
from math import pi
print("sciPy - pi = %.16f"%scipy.constants.pi)
print("math - pi = %.16f"%math.pi)Il programma precedente genererà il seguente output.
sciPy - pi = 3.1415926535897931
math - pi = 3.1415926535897931Elenco delle costanti disponibili
Le tabelle seguenti descrivono brevemente le varie costanti.
Costanti matematiche
| Sr. No. | Costante | Descrizione |
|---|---|---|
| 1 | pi | pi |
| 2 | d'oro | Rapporto aureo |
Costanti fisiche
La tabella seguente elenca le costanti fisiche più comunemente utilizzate.
| Sr. No. | Costante e descrizione |
|---|---|
| 1 | c Velocità della luce nel vuoto |
| 2 | speed_of_light Velocità della luce nel vuoto |
| 3 | h Costante di Planck |
| 4 | Planck Costante di Planck h |
| 5 | G Costante gravitazionale di Newton |
| 6 | e Carica elementare |
| 7 | R Costante molare dei gas |
| 8 | Avogadro Costante di Avogadro |
| 9 | k Costante di Boltzmann |
| 10 | electron_mass(OR) m_e Massa elettronica |
| 11 | proton_mass (OR) m_p Massa protonica |
| 12 | neutron_mass(OR)m_n Massa di neutroni |
Unità
La tabella seguente contiene l'elenco delle unità SI.
| Sr. No. | Unità | Valore |
|---|---|---|
| 1 | milli | 0.001 |
| 2 | micro | 1e-06 |
| 3 | chilo | 1000 |
Queste unità vanno da yotta, zetta, exa, peta, tera …… kilo, hector,… nano, pico,… a zepto.
Altre costanti importanti
La tabella seguente elenca altre importanti costanti utilizzate in SciPy.
| Sr. No. | Unità | Valore |
|---|---|---|
| 1 | grammo | 0,001 kg |
| 2 | massa atomica | Costante di massa atomica |
| 3 | grado | Laurea in radianti |
| 4 | minuto | Un minuto in secondi |
| 5 | giorno | Un giorno in pochi secondi |
| 6 | pollice | Un pollice in metri |
| 7 | micron | Un micron in metri |
| 8 | anno luce | Un anno luce in metri |
| 9 | ATM | Atmosfera standard in pascal |
| 10 | acro | Un acro in metri quadrati |
| 11 | litro | Un litro in metri cubi |
| 12 | gallone | Un gallone in metri cubi |
| 13 | kmh | Chilometri orari in metri al secondo |
| 14 | grado_Fahrenheit | Un Fahrenheit in kelvin |
| 15 | eV | Un elettronvolt in joule |
| 16 | hp | Una potenza in watt |
| 17 | dyn | Un dyne in newton |
| 18 | lambda2nu | Converti la lunghezza d'onda in frequenza ottica |
Ricordare tutto questo è un po 'difficile. Il modo più semplice per ottenere quale chiave è per quale funzione è conscipy.constants.find()metodo. Consideriamo il seguente esempio.
import scipy.constants
res = scipy.constants.physical_constants["alpha particle mass"]
print resIl programma precedente genererà il seguente output.
[
'alpha particle mass',
'alpha particle mass energy equivalent',
'alpha particle mass energy equivalent in MeV',
'alpha particle mass in u',
'electron to alpha particle mass ratio'
]Questo metodo restituisce l'elenco delle chiavi, altrimenti nulla se la parola chiave non corrisponde.
Fourier Transformationviene calcolato su un segnale nel dominio del tempo per verificarne il comportamento nel dominio della frequenza. La trasformazione di Fourier trova la sua applicazione in discipline come l'elaborazione del segnale e del rumore, l'elaborazione delle immagini, l'elaborazione del segnale audio, ecc. SciPy offre il modulo fftpack, che consente all'utente di calcolare rapide trasformate di Fourier.
Di seguito è riportato un esempio di una funzione seno, che verrà utilizzata per calcolare la trasformata di Fourier utilizzando il modulo fftpack.
Trasformata di Fourier veloce
Cerchiamo di capire in dettaglio cos'è la trasformata di Fourier veloce.
Trasformata di Fourier discreta unidimensionale
La FFT y [k] di lunghezza N della sequenza di lunghezza N x [n] viene calcolata da fft () e la trasformata inversa viene calcolata utilizzando ifft (). Consideriamo il seguente esempio
#Importing the fft and inverse fft functions from fftpackage
from scipy.fftpack import fft
#create an array with random n numbers
x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
#Applying the fft function
y = fft(x)
print yIl programma precedente genererà il seguente output.
[ 4.50000000+0.j 2.08155948-1.65109876j -1.83155948+1.60822041j
-1.83155948-1.60822041j 2.08155948+1.65109876j ]Vediamo un altro esempio
#FFT is already in the workspace, using the same workspace to for inverse transform
yinv = ifft(y)
print yinvIl programma precedente genererà il seguente output.
[ 1.0+0.j 2.0+0.j 1.0+0.j -1.0+0.j 1.5+0.j ]Il scipy.fftpackil modulo consente di calcolare trasformate di Fourier veloci. A titolo illustrativo, un segnale di ingresso (rumoroso) può apparire come segue:
import numpy as np
time_step = 0.02
period = 5.
time_vec = np.arange(0, 20, time_step)
sig = np.sin(2 * np.pi / period * time_vec) + 0.5 *np.random.randn(time_vec.size)
print sig.sizeStiamo creando un segnale con un passo temporale di 0,02 secondi. L'ultima istruzione stampa la dimensione del segnale sig. L'output sarebbe il seguente:
1000Non conosciamo la frequenza del segnale; conosciamo solo il passo del tempo di campionamento del segnale sig. Il segnale dovrebbe provenire da una funzione reale, quindi la trasformata di Fourier sarà simmetrica. Ilscipy.fftpack.fftfreq() la funzione genererà le frequenze di campionamento e scipy.fftpack.fft() calcolerà la trasformata veloce di Fourier.
Cerchiamo di capirlo con l'aiuto di un esempio.
from scipy import fftpack
sample_freq = fftpack.fftfreq(sig.size, d = time_step)
sig_fft = fftpack.fft(sig)
print sig_fftIl programma precedente genererà il seguente output.
array([
25.45122234 +0.00000000e+00j, 6.29800973 +2.20269471e+00j,
11.52137858 -2.00515732e+01j, 1.08111300 +1.35488579e+01j,
…….])Trasformata discreta del coseno
UN Discrete Cosine Transform (DCT)esprime una sequenza finita di punti dati in termini di una somma di funzioni del coseno che oscillano a frequenze diverse. SciPy fornisce un DCT con la funzionedct e un IDCT corrispondente con la funzione idct. Consideriamo il seguente esempio.
from scipy.fftpack import dct
print dct(np.array([4., 3., 5., 10., 5., 3.]))Il programma precedente genererà il seguente output.
array([ 60., -3.48476592, -13.85640646, 11.3137085, 6., -6.31319305])La trasformata inversa del coseno discreto ricostruisce una sequenza dai suoi coefficienti di trasformata discreta del coseno (DCT). La funzione idct è l'inverso della funzione dct. Cerchiamo di capirlo con il seguente esempio.
from scipy.fftpack import dct
print idct(np.array([4., 3., 5., 10., 5., 3.]))Il programma precedente genererà il seguente output.
array([ 39.15085889, -20.14213562, -6.45392043, 7.13341236,
8.14213562, -3.83035081])Quando una funzione non può essere integrata analiticamente, o è molto difficile da integrare analiticamente, si ricorre generalmente a metodi di integrazione numerica. SciPy ha una serie di routine per eseguire l'integrazione numerica. La maggior parte di loro si trovano nello stessoscipy.integratebiblioteca. La tabella seguente elenca alcune funzioni di uso comune.
| Suor No. | Descrizione della funzione |
|---|---|
| 1 | quad Integrazione unica |
| 2 | dblquad Doppia integrazione |
| 3 | tplquad Tripla integrazione |
| 4 | nquad n -fold integrazione multipla |
| 5 | fixed_quad Quadratura gaussiana, ordine n |
| 6 | quadrature Quadratura gaussiana alla tolleranza |
| 7 | romberg Integrazione di Romberg |
| 8 | trapz Regola trapezoidale |
| 9 | cumtrapz Regola trapezoidale per calcolare cumulativamente l'integrale |
| 10 | simps La regola di Simpson |
| 11 | romb Integrazione di Romberg |
| 12 | polyint Integrazione polinomiale analitica (NumPy) |
| 13 | poly1d Funzione di aiuto per polyint (NumPy) |
Integrali singoli
La funzione Quad è il cavallo di battaglia delle funzioni di integrazione di SciPy. A volte viene chiamata integrazione numericaquadrature, da qui il nome. Normalmente è la scelta predefinita per eseguire singoli integrali di una funzione f (x) su un dato intervallo fisso da a a b.
$$\int_{a}^{b} f(x)dx$$
La forma generale del quad è scipy.integrate.quad(f, a, b), Dove "f" è il nome della funzione da integrare. Mentre "a" e "b" sono rispettivamente i limiti inferiore e superiore. Vediamo un esempio della funzione gaussiana, integrata su un intervallo di 0 e 1.
Dobbiamo prima definire la funzione → $f(x) = e^{-x^2}$ , questo può essere fatto usando un'espressione lambda e quindi chiama il metodo quad su quella funzione.
import scipy.integrate
from numpy import exp
f= lambda x:exp(-x**2)
i = scipy.integrate.quad(f, 0, 1)
print iIl programma precedente genererà il seguente output.
(0.7468241328124271, 8.291413475940725e-15)La funzione quad restituisce i due valori, in cui il primo numero è il valore dell'integrale e il secondo valore è la stima dell'errore assoluto nel valore dell'integrale.
Note- Poiché quad richiede la funzione come primo argomento, non possiamo passare direttamente exp come argomento. La funzione Quad accetta l'infinito positivo e negativo come limiti. La funzione Quad può integrare funzioni NumPy standard predefinite di una singola variabile, come exp, sin e cos.
Integrali multipli
La meccanica per la doppia e tripla integrazione è stata racchiusa nelle funzioni dblquad, tplquad e nquad. Queste funzioni integrano rispettivamente quattro o sei argomenti. I limiti di tutti gli integrali interni devono essere definiti come funzioni.
Doppi integrali
La forma generale di dblquadè scipy.integrate.dblquad (func, a, b, gfun, hfun). Dove, func è il nome della funzione da integrare, 'a' e 'b' sono i limiti inferiore e superiore della variabile x, rispettivamente, mentre gfun e hfun sono i nomi delle funzioni che definiscono i limiti inferiore e superiore della variabile y.
Ad esempio, eseguiamo il metodo del doppio integrale.
$$\int_{0}^{1/2} dy \int_{0}^{\sqrt{1-4y^2}} 16xy \:dx$$
Definiamo le funzioni f, g e h, utilizzando le espressioni lambda. Si noti che anche se g e h sono costanti, come possono essere in molti casi, devono essere definite come funzioni, come abbiamo fatto qui per il limite inferiore.
import scipy.integrate
from numpy import exp
from math import sqrt
f = lambda x, y : 16*x*y
g = lambda x : 0
h = lambda y : sqrt(1-4*y**2)
i = scipy.integrate.dblquad(f, 0, 0.5, g, h)
print iIl programma precedente genererà il seguente output.
(0.5, 1.7092350012594845e-14)Oltre alle routine descritte sopra, scipy.integrate ha una serie di altre routine di integrazione, tra cui nquad, che esegue un'integrazione multipla n-fold, così come altre routine che implementano vari algoritmi di integrazione. Tuttavia, quad e dblquad soddisferanno la maggior parte delle nostre esigenze di integrazione numerica.
In questo capitolo, discuteremo di come l'interpolazione aiuta in SciPy.
Cos'è l'interpolazione?
L'interpolazione è il processo per trovare un valore tra due punti su una linea o una curva. Per aiutarci a ricordare cosa significa, dovremmo pensare alla prima parte della parola, "inter", che significa "entrare", che ci ricorda di guardare "dentro" i dati che avevamo originariamente. Questo strumento, l'interpolazione, non è solo utile nelle statistiche, ma è anche utile nella scienza, negli affari o quando è necessario prevedere valori che rientrano in due punti dati esistenti.
Creiamo alcuni dati e vediamo come questa interpolazione può essere eseguita utilizzando il scipy.interpolate pacchetto.
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
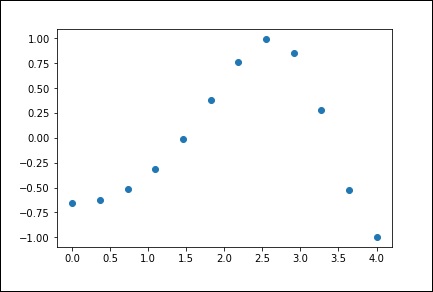
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print x,yIl programma precedente genererà il seguente output.
(
array([0., 0.36363636, 0.72727273, 1.09090909, 1.45454545, 1.81818182,
2.18181818, 2.54545455, 2.90909091, 3.27272727, 3.63636364, 4.]),
array([-0.65364362, -0.61966189, -0.51077021, -0.31047698, -0.00715476,
0.37976236, 0.76715099, 0.99239518, 0.85886263, 0.27994201,
-0.52586509, -0.99582185])
)Ora abbiamo due array. Supponendo che questi due array siano le due dimensioni dei punti nello spazio, tracciamo utilizzando il seguente programma e vediamo come appaiono.
plt.plot(x, y,’o’)
plt.show()Il programma precedente genererà il seguente output.
Interpolazione 1-D
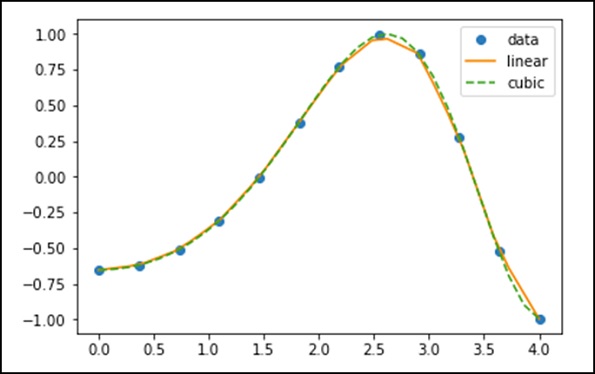
La classe interp1d in scipy.interpolate è un metodo conveniente per creare una funzione basata su punti dati fissi, che possono essere valutati ovunque all'interno del dominio definito dai dati forniti utilizzando l'interpolazione lineare.
Utilizzando i dati precedenti, creiamo una funzione di interpolazione e disegniamo un nuovo grafico interpolato.
f1 = interp1d(x, y,kind = 'linear')
f2 = interp1d(x, y, kind = 'cubic')Utilizzando la funzione interp1d, abbiamo creato due funzioni f1 e f2. Queste funzioni, per un dato input, x restituisce y. Il terzo tipo di variabile rappresenta il tipo di tecnica di interpolazione. "Linear", "Nearest", "Zero", "Slinear", "Quadratic", "Cubic" sono alcune tecniche di interpolazione.
Ora, creiamo un nuovo input di maggiore lunghezza per vedere la chiara differenza di interpolazione. Useremo la stessa funzione dei vecchi dati sui nuovi dati.
xnew = np.linspace(0, 4,30)
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')
plt.show()Il programma precedente genererà il seguente output.
Spline
Per disegnare curve morbide attraverso i punti dati, i disegnatori una volta usavano sottili strisce flessibili di legno, gomma dura, metallo o plastica chiamate spline meccaniche. Per utilizzare una spline meccanica, i perni sono stati posizionati in una selezione giudiziosa di punti lungo una curva in un disegno, quindi la spline è stata piegata, in modo che toccasse ciascuno di questi perni.
Chiaramente, con questa costruzione, la spline interpola la curva in corrispondenza di questi pin. Può essere utilizzato per riprodurre la curva in altri disegni. I punti in cui si trovano i perni sono chiamati nodi. Possiamo cambiare la forma della curva definita dalla spline regolando la posizione dei nodi.
Spline univariata
La spline di levigatura unidimensionale si adatta a un determinato insieme di punti dati. La classe UnivariateSpline in scipy.interpolate è un metodo conveniente per creare una funzione, basata sulla classe di punti dati fissi: scipy.interpolate.UnivariateSpline (x, y, w = None, bbox = [None, None], k = 3, s = Nessuno, ext = 0, check_finite = False).
Parameters - Di seguito sono riportati i parametri di una spline univariata.
Ciò adatta una spline y = spl (x) di grado k ai dati x, y forniti.
'w' - Specifica i pesi per l'adattamento della spline. Deve essere positivo. Se nessuno (impostazione predefinita), i pesi sono tutti uguali.
's' - Specifica il numero di nodi specificando una condizione di smussatura.
'k' - Grado della scanalatura di levigatura. Deve essere <= 5. L'impostazione predefinita è k = 3, una spline cubica.
Ext - Controlla la modalità di estrapolazione per gli elementi non nell'intervallo definito dalla sequenza di nodi.
se ext = 0 o 'estrapolare', restituisce il valore estrapolato.
se ext = 1 o 'zero', restituisce 0
se ext = 2 o 'raise', solleva un'eccezione ValueError
se ext = 3 di 'const', restituisce il valore limite.
check_finite - Indica se controllare che gli array di input contengano solo numeri finiti.
Consideriamo il seguente esempio.
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()Usa il valore predefinito per il parametro smoothing.
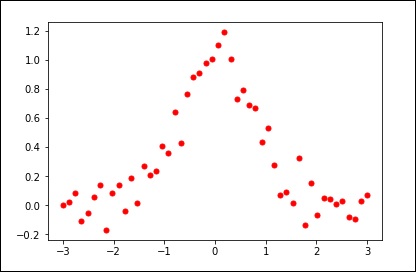
spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()Modificare manualmente la quantità di levigatura.
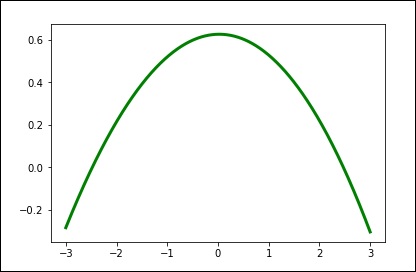
spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()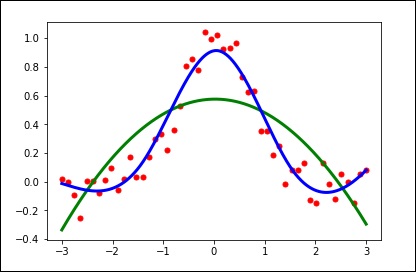
Il pacchetto Scipy.io (Input and Output) fornisce un'ampia gamma di funzioni per lavorare con diversi formati di file. Alcuni di questi formati sono:
- Matlab
- IDL
- Mercato Matrix
- Wave
- Arff
- Netcdf, ecc.
Parliamo in dettaglio dei formati di file più comunemente usati -
MATLAB
Di seguito sono riportate le funzioni utilizzate per caricare e salvare un file .mat.
| Sr. No. | Descrizione della funzione |
|---|---|
| 1 | loadmat Carica un file MATLAB |
| 2 | savemat Salva un file MATLAB |
| 3 | whosmat Elenca le variabili all'interno di un file MATLAB |
Consideriamo il seguente esempio.
import scipy.io as sio
import numpy as np
#Save a mat file
vect = np.arange(10)
sio.savemat('array.mat', {'vect':vect})
#Now Load the File
mat_file_content = sio.loadmat(‘array.mat’)
Print mat_file_contentIl programma precedente genererà il seguente output.
{
'vect': array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]), '__version__': '1.0',
'__header__': 'MATLAB 5.0 MAT-file Platform: posix, Created on: Sat Sep 30
09:49:32 2017', '__globals__': []
}Possiamo vedere l'array insieme alle informazioni Meta. Se vogliamo ispezionare il contenuto di un file MATLAB senza leggere i dati in memoria, usa l'estensionewhosmat command come mostrato di seguito.
import scipy.io as sio
mat_file_content = sio.whosmat(‘array.mat’)
print mat_file_contentIl programma precedente genererà il seguente output.
[('vect', (1, 10), 'int64')]SciPy è costruito utilizzando il file ottimizzato ATLAS LAPACK e BLASbiblioteche. Ha capacità di algebra lineare molto veloci. Tutte queste routine di algebra lineare prevedono un oggetto che può essere convertito in un array bidimensionale. Anche l'output di queste routine è un array bidimensionale.
SciPy.linalg contro NumPy.linalg
Un scipy.linalg contiene tutte le funzioni che sono in numpy.linalg. Inoltre, scipy.linalg ha anche altre funzioni avanzate che non sono in numpy.linalg. Un altro vantaggio dell'utilizzo di scipy.linalg su numpy.linalg è che è sempre compilato con il supporto BLAS / LAPACK, mentre per NumPy questo è opzionale. Pertanto, la versione SciPy potrebbe essere più veloce a seconda di come è stato installato NumPy.
Equazioni lineari
Il scipy.linalg.solve risolve l'equazione lineare a * x + b * y = Z, per i valori x, y sconosciuti.
Ad esempio, supponiamo che si desideri risolvere le seguenti equazioni simultanee.
x + 3y + 5z = 10
2x + 5y + z = 8
2x + 3y + 8z = 3
Per risolvere l'equazione precedente per i valori x, y, z, possiamo trovare il vettore della soluzione usando una matrice inversa come mostrato di seguito.
$$\begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8 \end{bmatrix}^{-1} \begin{bmatrix} 10\\ 8\\ 3 \end{bmatrix} = \frac{1}{25} \begin{bmatrix} -232\\ 129\\ 19 \end{bmatrix} = \begin{bmatrix} -9.28\\ 5.16\\ 0.76 \end{bmatrix}.$$
Tuttavia, è meglio usare l'estensione linalg.solve comando, che può essere più veloce e numericamente più stabile.
La funzione di risoluzione accetta due input "a" e "b" in cui "a" rappresenta i coefficienti e "b" rappresenta il rispettivo valore a destra e restituisce la matrice della soluzione.
Consideriamo il seguente esempio.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy arrays
a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])
b = np.array([2, 4, -1])
#Passing the values to the solve function
x = linalg.solve(a, b)
#printing the result array
print xIl programma precedente genererà il seguente output.
array([ 2., -2., 9.])Trovare un determinante
Il determinante di una matrice quadrata A è spesso indicato come | A | ed è una quantità spesso usata in algebra lineare. In SciPy, questo viene calcolato utilizzando ildet()funzione. Prende una matrice come input e restituisce un valore scalare.
Consideriamo il seguente esempio.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the det function
x = linalg.det(A)
#printing the result
print xIl programma precedente genererà il seguente output.
-2.0Autovalori e autovettori
Il problema autovalore-autovettore è una delle operazioni di algebra lineare più comunemente impiegate. Possiamo trovare i valori Eigen (λ) e i corrispondenti vettori Eigen (v) di una matrice quadrata (A) considerando la seguente relazione -
Av = λv
scipy.linalg.eigcalcola gli autovalori da un problema di autovalori ordinario o generalizzato. Questa funzione restituisce i valori Eigen e i vettori Eigen.
Consideriamo il seguente esempio.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the eig function
l, v = linalg.eig(A)
#printing the result for eigen values
print l
#printing the result for eigen vectors
print vIl programma precedente genererà il seguente output.
array([-0.37228132+0.j, 5.37228132+0.j]) #--Eigen Values
array([[-0.82456484, -0.41597356], #--Eigen Vectors
[ 0.56576746, -0.90937671]])Scomposizione di un valore singolo
Una decomposizione di valori singolari (SVD) può essere pensata come un'estensione del problema degli autovalori a matrici che non sono quadrate.
Il scipy.linalg.svd fattorizza la matrice 'a' in due matrici unitarie 'U' e 'Vh' e una matrice 1-D 's' di valori singolari (reali, non negativi) tali che a == U * S * Vh, dove 'S 'è una matrice di zeri di forma adeguata con la diagonale principale' s '.
Consideriamo il seguente esempio.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2)
#Passing the values to the eig function
U, s, Vh = linalg.svd(a)
# printing the result
print U, Vh, sIl programma precedente genererà il seguente output.
(
array([
[ 0.54828424-0.23329795j, -0.38465728+0.01566714j,
-0.18764355+0.67936712j],
[-0.27123194-0.5327436j , -0.57080163-0.00266155j,
-0.39868941-0.39729416j],
[ 0.34443818+0.4110186j , -0.47972716+0.54390586j,
0.25028608-0.35186815j]
]),
array([ 3.25745379, 1.16150607]),
array([
[-0.35312444+0.j , 0.32400401+0.87768134j],
[-0.93557636+0.j , -0.12229224-0.33127251j]
])
)Il sottomodulo SciPy ndimage è dedicato all'elaborazione delle immagini. Qui, ndimage significa un'immagine n-dimensionale.
Alcune delle attività più comuni nell'elaborazione delle immagini sono le seguenti & miuns;
- Input / Output, visualizzazione di immagini
- Manipolazioni di base: ritaglio, capovolgimento, rotazione, ecc.
- Filtro delle immagini: riduzione del rumore, nitidezza, ecc.
- Segmentazione dell'immagine: etichettatura dei pixel corrispondenti a oggetti diversi
- Classification
- Estrazione delle caratteristiche
- Registration
Parliamo di come alcuni di questi possono essere ottenuti utilizzando SciPy.
Apertura e scrittura su file immagine
Il misc packagein SciPy viene fornito con alcune immagini. Usiamo quelle immagini per imparare le manipolazioni delle immagini. Consideriamo il seguente esempio.
from scipy import misc
f = misc.face()
misc.imsave('face.png', f) # uses the Image module (PIL)
import matplotlib.pyplot as plt
plt.imshow(f)
plt.show()Il programma precedente genererà il seguente output.

Qualsiasi immagine nel suo formato grezzo è la combinazione di colori rappresentata dai numeri nel formato matrice. Una macchina comprende e manipola le immagini solo in base a quei numeri. RGB è un modo popolare di rappresentazione.
Vediamo le informazioni statistiche dell'immagine sopra.
from scipy import misc
face = misc.face(gray = False)
print face.mean(), face.max(), face.min()Il programma precedente genererà il seguente output.
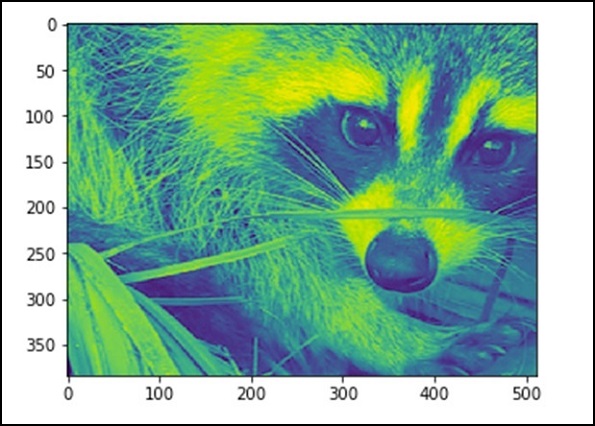
110.16274388631184, 255, 0Ora, sappiamo che l'immagine è composta da numeri, quindi qualsiasi cambiamento nel valore del numero altera l'immagine originale. Eseguiamo alcune trasformazioni geometriche sull'immagine. L'operazione geometrica di base è il ritaglio
from scipy import misc
face = misc.face(gray = True)
lx, ly = face.shape
# Cropping
crop_face = face[lx / 4: - lx / 4, ly / 4: - ly / 4]
import matplotlib.pyplot as plt
plt.imshow(crop_face)
plt.show()Il programma precedente genererà il seguente output.
Possiamo anche eseguire alcune operazioni di base come capovolgere l'immagine come descritto di seguito.
# up <-> down flip
from scipy import misc
face = misc.face()
flip_ud_face = np.flipud(face)
import matplotlib.pyplot as plt
plt.imshow(flip_ud_face)
plt.show()Il programma precedente genererà il seguente output.

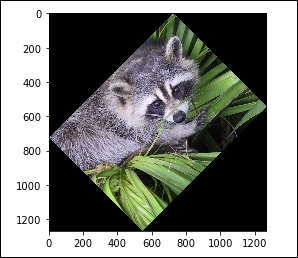
Oltre a questo, abbiamo il file rotate() function, che ruota l'immagine con un angolo specificato.
# rotation
from scipy import misc,ndimage
face = misc.face()
rotate_face = ndimage.rotate(face, 45)
import matplotlib.pyplot as plt
plt.imshow(rotate_face)
plt.show()Il programma precedente genererà il seguente output.
Filtri
Parliamo di come i filtri aiutano nell'elaborazione delle immagini.
Che cos'è il filtraggio nell'elaborazione delle immagini?
Il filtraggio è una tecnica per modificare o migliorare un'immagine. Ad esempio, puoi filtrare un'immagine per enfatizzare determinate caratteristiche o rimuovere altre caratteristiche. Le operazioni di elaborazione delle immagini implementate con il filtro includono Smoothing, Sharpening e Edge Enhancement.
Il filtraggio è un'operazione di vicinato, in cui il valore di un dato pixel nell'immagine di output viene determinato applicando un algoritmo ai valori dei pixel nelle vicinanze del pixel di input corrispondente. Eseguiamo ora alcune operazioni utilizzando SciPy ndimage.
Sfocatura
La sfocatura è ampiamente utilizzata per ridurre il rumore nell'immagine. Possiamo eseguire un'operazione di filtro e vedere la modifica nell'immagine. Consideriamo il seguente esempio.
from scipy import misc
face = misc.face()
blurred_face = ndimage.gaussian_filter(face, sigma=3)
import matplotlib.pyplot as plt
plt.imshow(blurred_face)
plt.show()Il programma precedente genererà il seguente output.

Il valore sigma indica il livello di sfocatura su una scala di cinque. Possiamo vedere il cambiamento sulla qualità dell'immagine regolando il valore sigma. Per maggiori dettagli sulla sfocatura, fare clic su → Tutorial DIP (Digital Image Processing).
Rilevamento dei bordi
Parliamo di come il rilevamento dei bordi aiuta nell'elaborazione delle immagini.
Cos'è Edge Detection?
Il rilevamento dei bordi è una tecnica di elaborazione delle immagini per trovare i confini degli oggetti all'interno delle immagini. Funziona rilevando discontinuità nella luminosità. Il rilevamento dei bordi viene utilizzato per la segmentazione delle immagini e l'estrazione dei dati in aree quali elaborazione di immagini, visione artificiale e visione artificiale.
Gli algoritmi di rilevamento dei bordi più comunemente utilizzati includono
- Sobel
- Canny
- Prewitt
- Roberts
- Metodi di logica fuzzy
Consideriamo il seguente esempio.
import scipy.ndimage as nd
import numpy as np
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
import matplotlib.pyplot as plt
plt.imshow(im)
plt.show()Il programma precedente genererà il seguente output.

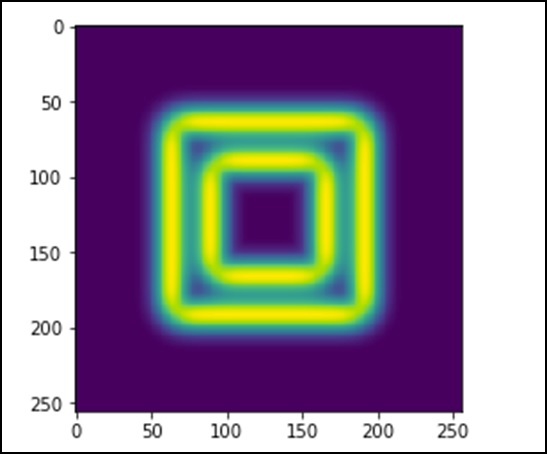
L'immagine sembra un blocco quadrato di colori. Ora rileveremo i bordi di quei blocchi colorati. Qui, ndimage fornisce una funzione chiamataSobelper eseguire questa operazione. Considerando che NumPy fornisce l'estensioneHypot funzione per combinare le due matrici risultanti in una.
Consideriamo il seguente esempio.
import scipy.ndimage as nd
import matplotlib.pyplot as plt
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
sx = ndimage.sobel(im, axis = 0, mode = 'constant')
sy = ndimage.sobel(im, axis = 1, mode = 'constant')
sob = np.hypot(sx, sy)
plt.imshow(sob)
plt.show()Il programma precedente genererà il seguente output.
Il scipy.optimize packagefornisce diversi algoritmi di ottimizzazione comunemente usati. Questo modulo contiene i seguenti aspetti:
Minimizzazione non vincolata e vincolata di funzioni scalari multivariate (minimizzare ()) utilizzando una varietà di algoritmi (ad esempio BFGS, Nelder-Mead simplex, Newton Conjugate Gradient, COBYLA o SLSQP)
Routine di ottimizzazione globale (forza bruta) (ad esempio, anneal (), bacinohopping ())
Algoritmi di minimizzazione dei minimi quadrati (leastsq ()) e adattamento della curva (curve_fit ())
Funzioni scalari univariate minimizzatori (minimizzare_scalar ()) e cercatori di radici (newton ())
Risolutori di sistemi di equazioni multivariati (root ()) che utilizzano una varietà di algoritmi (ad esempio Powell ibrido, Levenberg-Marquardt o metodi su larga scala come Newton-Krylov)
Minimizzazione non vincolata e vincolata di funzioni scalari multivariate
Il minimize() function fornisce un'interfaccia comune per algoritmi di minimizzazione non vincolati e vincolati per funzioni scalari multivariate in scipy.optimize. Per dimostrare la funzione di minimizzazione, si consideri il problema di minimizzare la funzione di Rosenbrock delle variabili NN -
$$f(x) = \sum_{i = 1}^{N-1} \:100(x_i - x_{i-1}^{2})$$
Il valore minimo di questa funzione è 0, che si ottiene quando xi = 1.
Algoritmo nelder – Mead simplex
Nell'esempio seguente, la routine minimum () viene utilizzata con il Nelder-Mead simplex algorithm (method = 'Nelder-Mead')(selezionato tramite il parametro del metodo). Consideriamo il seguente esempio.
import numpy as np
from scipy.optimize import minimize
def rosen(x):
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead')
print(res.x)Il programma precedente genererà il seguente output.
[7.93700741e+54 -5.41692163e+53 6.28769150e+53 1.38050484e+55 -4.14751333e+54]L'algoritmo simplex è probabilmente il modo più semplice per ridurre al minimo una funzione abbastanza ben comportata. Richiede solo valutazioni di funzione ed è una buona scelta per semplici problemi di minimizzazione. Tuttavia, poiché non utilizza valutazioni del gradiente, potrebbe essere necessario più tempo per trovare il minimo.
Un altro algoritmo di ottimizzazione che necessita solo di chiamate di funzione per trovare il minimo è il file Powell‘s method, disponibile impostando method = 'powell' nella funzione reduce ().
Minimi quadrati
Risolvi un problema dei minimi quadrati non lineari con limiti sulle variabili. Dati i residui f (x) (una funzione reale m-dimensionale di n variabili reali) e la funzione di perdita rho (s) (una funzione scalare), i minimi_quadrati trovano un minimo locale della funzione di costo F (x). Consideriamo il seguente esempio.
In questo esempio, troviamo un minimo della funzione di Rosenbrock senza limiti sulle variabili indipendenti.
#Rosenbrock Function
def fun_rosenbrock(x):
return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(fun_rosenbrock, input)
print resSi noti che forniamo solo il vettore dei residui. L'algoritmo costruisce la funzione di costo come somma dei quadrati dei residui, che dà la funzione di Rosenbrock. Il minimo esatto è x = [1.0,1.0].
Il programma precedente genererà il seguente output.
active_mask: array([ 0., 0.])
cost: 9.8669242910846867e-30
fun: array([ 4.44089210e-15, 1.11022302e-16])
grad: array([ -8.89288649e-14, 4.44089210e-14])
jac: array([[-20.00000015,10.],[ -1.,0.]])
message: '`gtol` termination condition is satisfied.'
nfev: 3
njev: 3
optimality: 8.8928864934219529e-14
status: 1
success: True
x: array([ 1., 1.])Ricerca delle radici
Facci capire come la ricerca delle radici aiuta in SciPy.
Funzioni scalari
Se si ha un'equazione a variabile singola, ci sono quattro diversi algoritmi di ricerca delle radici, che possono essere provati. Ciascuno di questi algoritmi richiede gli endpoint di un intervallo in cui è prevista una radice (poiché la funzione cambia segno). In generale,brentq è la scelta migliore, ma gli altri metodi possono essere utili in determinate circostanze o per scopi accademici.
Risoluzione a virgola fissa
Un problema strettamente correlato alla ricerca degli zeri di una funzione è il problema di trovare un punto fisso di una funzione. Un punto fisso di una funzione è il punto in cui la valutazione della funzione restituisce il punto: g (x) = x. Chiaramente il punto fermo diggè la radice di f (x) = g (x) −x. Allo stesso modo, la radice diffè il punto_fisso di g (x) = f (x) + x. La routine fixed_point fornisce un semplice metodo iterativo utilizzando ilAitkens sequence acceleration stimare il punto fisso di gg, se viene fornito un punto di partenza.
Insiemi di equazioni
Trovare una radice di un insieme di equazioni non lineari può essere ottenuto utilizzando il root() function. Sono disponibili diversi metodi, tra cuihybr (il valore predefinito) e lm, usano rispettivamente il hybrid method of Powell e il Levenberg-Marquardt method dal MINPACK.
L'esempio seguente considera l'equazione trascendentale a variabile singola.
x2 + 2cos(x) = 0
Una radice di cui può essere trovata come segue -
import numpy as np
from scipy.optimize import root
def func(x):
return x*2 + 2 * np.cos(x)
sol = root(func, 0.3)
print solIl programma precedente genererà il seguente output.
fjac: array([[-1.]])
fun: array([ 2.22044605e-16])
message: 'The solution converged.'
nfev: 10
qtf: array([ -2.77644574e-12])
r: array([-3.34722409])
status: 1
success: True
x: array([-0.73908513])Tutte le funzioni statistiche si trovano nel sottopacchetto scipy.stats e un elenco abbastanza completo di queste funzioni può essere ottenuto utilizzando info(stats)funzione. È inoltre possibile ottenere un elenco di variabili casuali disponibili daldocstringper il sottopacchetto delle statistiche. Questo modulo contiene un gran numero di distribuzioni di probabilità e una crescente libreria di funzioni statistiche.
Ogni distribuzione univariata ha la propria sottoclasse come descritto nella tabella seguente:
| Sr. No. | Classe e descrizione |
|---|---|
| 1 | rv_continuous Una classe di variabile casuale continua generica destinata alla sottoclasse |
| 2 | rv_discrete Una classe di variabile casuale discreta generica destinata alla sottoclasse |
| 3 | rv_histogram Genera una distribuzione data da un istogramma |
Variabile casuale continua normale
Una distribuzione di probabilità in cui la variabile casuale X può assumere qualsiasi valore è una variabile casuale continua. La parola chiave location (loc) specifica la media. La parola chiave scale (scale) specifica la deviazione standard.
Come istanza di rv_continuous classe, norm object eredita da esso una raccolta di metodi generici e li completa con dettagli specifici per questa particolare distribuzione.
Per calcolare il CDF in un certo numero di punti, possiamo passare un elenco o un array NumPy. Consideriamo il seguente esempio.
from scipy.stats import norm
import numpy as np
print norm.cdf(np.array([1,-1., 0, 1, 3, 4, -2, 6]))Il programma precedente genererà il seguente output.
array([ 0.84134475, 0.15865525, 0.5 , 0.84134475, 0.9986501 ,
0.99996833, 0.02275013, 1. ])Per trovare la mediana di una distribuzione, possiamo usare la funzione del punto percentuale (PPF), che è l'inverso della CDF. Facci capire usando il seguente esempio.
from scipy.stats import norm
print norm.ppf(0.5)Il programma precedente genererà il seguente output.
0.0Per generare una sequenza di variabili casuali, dovremmo usare l'argomento della parola chiave size, mostrato nell'esempio seguente.
from scipy.stats import norm
print norm.rvs(size = 5)Il programma precedente genererà il seguente output.
array([ 0.20929928, -1.91049255, 0.41264672, -0.7135557 , -0.03833048])L'output di cui sopra non è riproducibile. Per generare gli stessi numeri casuali, usa la funzione seed.
Distribuzione uniforme
Una distribuzione uniforme può essere generata utilizzando la funzione uniform. Consideriamo il seguente esempio.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)Il programma precedente genererà il seguente output.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])Crea una distribuzione discreta
Generiamo un campione casuale e confrontiamo le frequenze osservate con le probabilità.
Distribuzione binomiale
Come istanza di rv_discrete class, il binom objecteredita da esso una raccolta di metodi generici e li completa con dettagli specifici per questa particolare distribuzione. Consideriamo il seguente esempio.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)Il programma precedente genererà il seguente output.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])Statistiche descrittive
Le statistiche di base come Min, Max, Mean e Variance prendono l'array NumPy come input e restituiscono i rispettivi risultati. Alcune funzioni statistiche di base disponibili inscipy.stats package sono descritti nella tabella seguente.
| Sr. No. | Descrizione della funzione |
|---|---|
| 1 | describe() Calcola diverse statistiche descrittive dell'array passato |
| 2 | gmean() Calcola la media geometrica lungo l'asse specificato |
| 3 | hmean() Calcola la media armonica lungo l'asse specificato |
| 4 | kurtosis() Calcola la curtosi |
| 5 | mode() Restituisce il valore modale |
| 6 | skew() Verifica l'asimmetria dei dati |
| 7 | f_oneway() Esegue un'ANOVA a 1 via |
| 8 | iqr() Calcola l'intervallo interquartile dei dati lungo l'asse specificato |
| 9 | zscore() Calcola il punteggio z di ciascun valore nel campione, relativo alla media del campione e alla deviazione standard |
| 10 | sem() Calcola l'errore standard della media (o errore standard di misurazione) dei valori nella matrice di input |
Molte di queste funzioni hanno una versione simile in scipy.stats.mstats, che funzionano per array mascherati. Cerchiamo di capire questo con l'esempio fornito di seguito.
from scipy import stats
import numpy as np
x = np.array([1,2,3,4,5,6,7,8,9])
print x.max(),x.min(),x.mean(),x.var()Il programma precedente genererà il seguente output.
(9, 1, 5.0, 6.666666666666667)T-test
Cerchiamo di capire come T-test è utile in SciPy.
ttest_1samp
Calcola il test T per la media di UN gruppo di punteggi. Questo è un test bilaterale per l'ipotesi nulla che il valore atteso (media) di un campione di osservazioni indipendenti 'a' sia uguale alla media della popolazione data,popmean. Consideriamo il seguente esempio.
from scipy import stats
rvs = stats.norm.rvs(loc = 5, scale = 10, size = (50,2))
print stats.ttest_1samp(rvs,5.0)Il programma precedente genererà il seguente output.
Ttest_1sampResult(statistic = array([-1.40184894, 2.70158009]),
pvalue = array([ 0.16726344, 0.00945234]))Confrontando due campioni
Negli esempi seguenti, ci sono due campioni, che possono provenire dalla stessa o da una distribuzione diversa, e vogliamo verificare se questi campioni hanno le stesse proprietà statistiche.
ttest_ind- Calcola il test T per la media di due campioni indipendenti di punteggi. Questo è un test bilaterale per l'ipotesi nulla che due campioni indipendenti abbiano valori medi (attesi) identici. Questo test presume che le popolazioni abbiano varianze identiche per impostazione predefinita.
Possiamo usare questo test, se osserviamo due campioni indipendenti della stessa o diversa popolazione. Consideriamo il seguente esempio.
from scipy import stats
rvs1 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
rvs2 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
print stats.ttest_ind(rvs1,rvs2)Il programma precedente genererà il seguente output.
Ttest_indResult(statistic = -0.67406312233650278, pvalue = 0.50042727502272966)Puoi testare lo stesso con un nuovo array della stessa lunghezza, ma con una media varia. Utilizza un valore diverso inloc e prova lo stesso.
CSGraph sta per Compressed Sparse Graph, che si concentra su algoritmi di grafi veloci basati su rappresentazioni di matrici sparse.
Rappresentazioni grafiche
Per cominciare, cerchiamo di capire cos'è un grafo sparse e come aiuta nelle rappresentazioni grafiche.
Cos'è esattamente un grafico sparse?
Un grafico è solo una raccolta di nodi, che hanno collegamenti tra di loro. I grafici possono rappresentare quasi tutto: connessioni di social network, in cui ogni nodo è una persona ed è connesso a conoscenti; immagini, dove ogni nodo è un pixel ed è connesso ai pixel vicini; punti in una distribuzione ad alta dimensione, dove ogni nodo è connesso ai suoi vicini più prossimi; e praticamente qualsiasi altra cosa tu possa immaginare.
Un modo molto efficiente per rappresentare i dati del grafo è in una matrice sparsa: chiamiamola G. La matrice G è di dimensione N x N, e G [i, j] fornisce il valore della connessione tra il nodo 'i' e il nodo 'j'. Un grafo sparso contiene principalmente zeri, ovvero la maggior parte dei nodi ha solo poche connessioni. Questa proprietà risulta essere vera nella maggior parte dei casi di interesse.
La creazione del sottomodulo del grafo sparse è stata motivata da diversi algoritmi utilizzati in scikit-learn che includevano quanto segue:
Isomap - Un algoritmo di apprendimento molteplice, che richiede di trovare i percorsi più brevi in un grafico.
Hierarchical clustering - Un algoritmo di clustering basato su uno spanning tree minimo.
Spectral Decomposition - Un algoritmo di proiezione basato su laplaciani di grafi sparsi.
Come esempio concreto, immagina di voler rappresentare il seguente grafico non orientato:
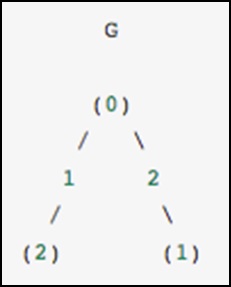
Questo grafico ha tre nodi, dove i nodi 0 e 1 sono collegati da un bordo di peso 2, ei nodi 0 e 2 sono collegati da un bordo di peso 1. Possiamo costruire le rappresentazioni dense, mascherate e sparse come mostrato nell'esempio seguente , tenendo presente che un grafo non orientato è rappresentato da una matrice simmetrica.
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.dataIl programma precedente genererà il seguente output.
array([2, 1, 2, 1])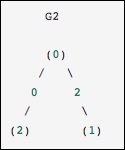
Questo è identico al grafico precedente, tranne per il fatto che i nodi 0 e 2 sono collegati da un bordo di peso zero. In questo caso, la rappresentazione densa sopra porta ad ambiguità: come possono essere rappresentati i non bordi, se zero è un valore significativo. In questo caso, è necessario utilizzare una rappresentazione mascherata o sparsa per eliminare l'ambiguità.
Consideriamo il seguente esempio.
from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
[np.inf, 2, 0 ],
[2, np.inf, np.inf],
[0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.dataIl programma precedente genererà il seguente output.
array([ 2., 0., 2., 0.])Scale di parole che utilizzano grafici sparsi
Word ladders è un gioco inventato da Lewis Carroll, in cui le parole sono collegate cambiando una singola lettera ad ogni passaggio. Ad esempio:
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
Qui, siamo passati da "APE" a "MAN" in sette passaggi, cambiando ogni volta una lettera. La domanda è: possiamo trovare un percorso più breve tra queste parole usando la stessa regola? Questo problema è naturalmente espresso come un problema di grafi sparsi. I nodi corrisponderanno a singole parole e creeremo connessioni tra parole che differiscono al massimo di una lettera.
Ottenere un elenco di parole
Innanzitutto, ovviamente, dobbiamo ottenere un elenco di parole valide. Sto eseguendo Mac e Mac ha un dizionario di parole nella posizione indicata nel seguente blocco di codice. Se utilizzi un'architettura diversa, potresti dover cercare un po 'per trovare il dizionario di sistema.
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)Il programma precedente genererà il seguente output.
235886Ora vogliamo esaminare le parole di lunghezza 3, quindi selezioniamo solo quelle parole della lunghezza corretta. Elimineremo anche le parole che iniziano con lettere maiuscole (nomi propri) o contengono caratteri non alfanumerici come apostrofi e trattini. Infine, ci assicureremo che tutto sia in minuscolo per un confronto in seguito.
word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)Il programma precedente genererà il seguente output.
1135Ora, abbiamo un elenco di 1135 parole di tre lettere valide (il numero esatto può cambiare a seconda del particolare elenco utilizzato). Ognuna di queste parole diventerà un nodo nel nostro grafico e creeremo bordi che collegano i nodi associati a ciascuna coppia di parole, che differisce di una sola lettera.
import numpy as np
word_list = np.asarray(word_list)
word_list.dtype
word_list.sort()
word_bytes = np.ndarray((word_list.size, word_list.itemsize),
dtype = 'int8',
buffer = word_list.data)
print word_bytes.shapeIl programma precedente genererà il seguente output.
(1135, 3)Useremo la distanza di Hamming tra ogni punto per determinare quali coppie di parole sono collegate. La distanza di Hamming misura la frazione di voci tra due vettori, che differiscono: due parole qualsiasi con una distanza di martellamento uguale a 1 / N1 / N, dove NN è il numero di lettere, che sono collegate nella scala di parole.
from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))Quando confrontiamo le distanze, non usiamo l'uguaglianza perché può essere instabile per i valori in virgola mobile. La disuguaglianza produce il risultato desiderato purché non ci siano due voci dell'elenco di parole identiche. Ora che il nostro grafico è impostato, useremo la ricerca del percorso più breve per trovare il percorso tra due parole qualsiasi nel grafico.
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]Il programma precedente genererà il seguente output.
ape, manDobbiamo controllare che queste corrispondano, perché se le parole non sono nell'elenco ci sarà un errore nell'output. Ora, tutto ciò di cui abbiamo bisogno è trovare il percorso più breve tra questi due indici nel grafico. Noi useremodijkstra’s algoritmo, perché ci permette di trovare il percorso per un solo nodo.
from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]Il programma precedente genererà il seguente output.
5.0Quindi, vediamo che il percorso più breve tra "ape" e "man" contiene solo cinque passaggi. Possiamo usare i predecessori restituiti dall'algoritmo per ricostruire questo percorso.
path = []
i = i2
while i != i1:
path.append(word_list[i])
i = predecessors[i]
path.append(word_list[i1])
print path[::-1]i2]Il programma precedente genererà il seguente output.
['ape', 'ope', 'opt', 'oat', 'mat', 'man']Il scipy.spatial package può calcolare triangolazioni, diagrammi di Voronoi e scafi convessi di un insieme di punti, sfruttando il Qhull library. Inoltre, contieneKDTree implementations per le query del punto più vicino e le utilità per i calcoli della distanza in varie metriche.
Triangolazioni di Delaunay
Cerchiamo di capire cosa sono le triangolazioni di Delaunay e come vengono utilizzate in SciPy.
Cosa sono le triangolazioni di Delaunay?
In matematica e geometria computazionale, una triangolazione di Delaunay per un dato insieme P di punti discreti in un piano è una triangolazione DT(P) tale che non ha senso P è all'interno del circumcircle di qualsiasi triangolo in DT (P).
Possiamo calcolare lo stesso tramite SciPy. Consideriamo il seguente esempio.
from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()Il programma precedente genererà il seguente output.

Punti complanari
Cerchiamo di capire cosa sono i punti complanari e come vengono utilizzati in SciPy.
Cosa sono i punti complanari?
I punti complanari sono tre o più punti che giacciono sullo stesso piano. Ricorda che un piano è una superficie piatta, che si estende senza fine in tutte le direzioni. Di solito è mostrato nei libri di testo di matematica come una figura a quattro lati.
Vediamo come possiamo trovarlo usando SciPy. Consideriamo il seguente esempio.
from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanarIl programma precedente genererà il seguente output.
array([[4, 0, 3]], dtype = int32)Ciò significa che il punto 4 risiede vicino al triangolo 0 e al vertice 3, ma non è incluso nella triangolazione.
Scafi convessi
Cerchiamo di capire cosa sono gli scafi convessi e come vengono utilizzati in SciPy.
Cosa sono gli scafi convessi?
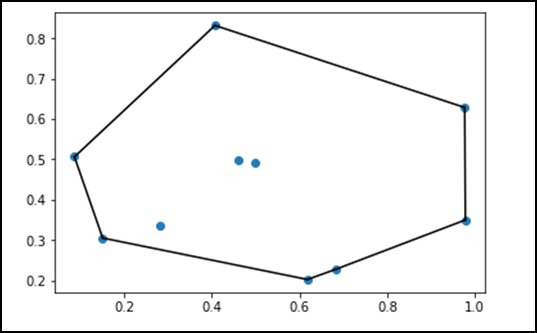
In matematica, il convex hull o convex envelope di un insieme di punti X nel piano euclideo o in uno spazio euclideo (o, più in generale, in uno spazio affine sui reali) è il più piccolo convex set che contiene X.
Consideriamo il seguente esempio per capirlo in dettaglio.
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()Il programma precedente genererà il seguente output.
ODR sta per Orthogonal Distance Regression, utilizzato negli studi di regressione. La regressione lineare di base viene spesso utilizzata per stimare la relazione tra le due variabiliy e x tracciando la linea che meglio si adatta al grafico.
Il metodo matematico utilizzato per questo è noto come Least Squarese mira a ridurre al minimo la somma dell'errore al quadrato per ogni punto. La domanda chiave qui è come si calcola l'errore (noto anche come residuo) per ogni punto?
In una regressione lineare standard, l'obiettivo è quello di prevedere il valore Y dal valore X, quindi la cosa sensata da fare è calcolare l'errore nei valori Y (mostrati come linee grigie nell'immagine seguente). Tuttavia, a volte è più sensato prendere in considerazione l'errore sia in X che in Y (come mostrato dalle linee rosse tratteggiate nell'immagine seguente).
Ad esempio: quando sai che le tue misurazioni di X sono incerte o quando non vuoi concentrarti sugli errori di una variabile rispetto a un'altra.
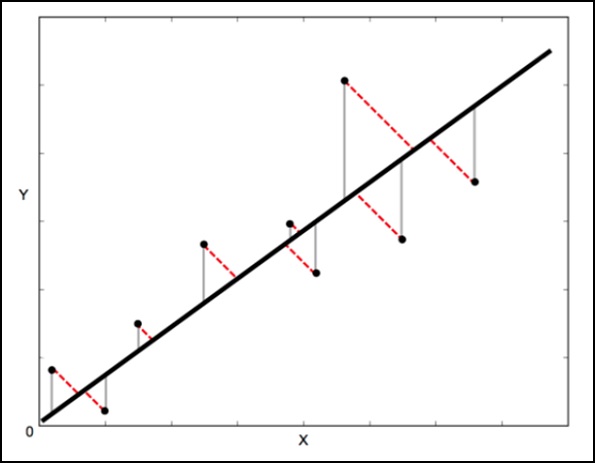
Orthogonal Distance Regression (ODR) è un metodo che può farlo (ortogonale in questo contesto significa perpendicolare, quindi calcola gli errori perpendicolari alla linea, piuttosto che solo "verticalmente").
Scipy.odr Implementazione per la regressione univariata
L'esempio seguente mostra l'implementazione di scipy.odr per la regressione univariata.
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()Il programma precedente genererà il seguente output.
Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [ 0.7786442 2.33126407]
Beta Covariance: [
[ 1.93150969 -4.82877433]
[ -4.82877433 17.31417201
]]
Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
Sum of squares convergenceLe funzioni disponibili nel pacchetto speciale sono funzioni universali, che seguono la trasmissione e il looping automatico dell'array.
Esaminiamo alcune delle funzioni speciali utilizzate più di frequente:
- Funzione radice cubica
- Funzione esponenziale
- Funzione esponenziale errore relativo
- Funzione esponenziale della somma dei registri
- Funzione di Lambert
- Funzione di permutazioni e combinazioni
- Funzione gamma
Vediamo ora di comprendere brevemente ciascuna di queste funzioni.
Funzione radice cubica
La sintassi di questa funzione radice cubica è - scipy.special.cbrt (x). Questo recupererà la radice cubica per elemento dix.
Consideriamo il seguente esempio.
from scipy.special import cbrt
res = cbrt([10, 9, 0.1254, 234])
print resIl programma precedente genererà il seguente output.
[ 2.15443469 2.08008382 0.50053277 6.16224015]Funzione esponenziale
La sintassi della funzione esponenziale è - scipy.special.exp10 (x). Questo calcolerà 10 ** x elemento saggio.
Consideriamo il seguente esempio.
from scipy.special import exp10
res = exp10([2, 9])
print resIl programma precedente genererà il seguente output.
[1.00000000e+02 1.00000000e+09]Funzione esponenziale errore relativo
La sintassi per questa funzione è: scipy.special.exprel (x). Genera l'errore relativo esponenziale, (exp (x) - 1) / x.
quando xè vicino a zero, exp (x) è vicino a 1, quindi il calcolo numerico di exp (x) - 1 può subire una perdita catastrofica di precisione. Quindi viene implementato exprel (x) per evitare la perdita di precisione, che si verifica quandox è vicino allo zero.
Consideriamo il seguente esempio.
from scipy.special import exprel
res = exprel([-0.25, -0.1, 0, 0.1, 0.25])
print resIl programma precedente genererà il seguente output.
[0.88479687 0.95162582 1. 1.05170918 1.13610167]Funzione esponenziale della somma dei registri
La sintassi per questa funzione è: scipy.special.logsumexp (x). Aiuta a calcolare il registro della somma degli esponenziali degli elementi di input.
Consideriamo il seguente esempio.
from scipy.special import logsumexp
import numpy as np
a = np.arange(10)
res = logsumexp(a)
print resIl programma precedente genererà il seguente output.
9.45862974443Funzione di Lambert
La sintassi per questa funzione è: scipy.special.lambertw (x). È anche chiamata funzione Lambert W. La funzione W di Lambert W (z) è definita come la funzione inversa di w * exp (w). In altre parole, il valore di W (z) è tale che z = W (z) * exp (W (z)) per qualsiasi numero complesso z.
La funzione Lambert W è una funzione multivalore con infiniti rami. Ogni ramo fornisce una soluzione separata dell'equazione z = w exp (w). Qui, i rami sono indicizzati dall'intero k.
Consideriamo il seguente esempio. Qui, la funzione W di Lambert è l'inversa di w exp (w).
from scipy.special import lambertw
w = lambertw(1)
print w
print w * np.exp(w)Il programma precedente genererà il seguente output.
(0.56714329041+0j)
(1+0j)Permutazioni e combinazioni
Parliamo di permutazioni e combinazioni separatamente per comprenderle chiaramente.
Combinations- La sintassi per la funzione di combinazione è - scipy.special.comb (N, k). Consideriamo il seguente esempio:
from scipy.special import comb
res = comb(10, 3, exact = False,repetition=True)
print resIl programma precedente genererà il seguente output.
220.0Note- Gli argomenti della matrice sono accettati solo per il caso esatto = Falso. Se k> N, N <0 o k <0, viene restituito uno 0.
Permutations- La sintassi per la funzione di combinazione è - scipy.special.perm (N, k). Permutazioni di N cose prese k alla volta, cioè k-permutazioni di N. Questo è anche noto come "permutazioni parziali".
Consideriamo il seguente esempio.
from scipy.special import perm
res = perm(10, 3, exact = True)
print resIl programma precedente genererà il seguente output.
720Funzione gamma
La funzione gamma viene spesso definita fattoriale generalizzata poiché z * gamma (z) = gamma (z + 1) e gamma (n + 1) = n !, per un numero naturale 'n'.
La sintassi per la funzione di combinazione è - scipy.special.gamma (x). Permutazioni di N cose prese k alla volta, cioè k-permutazioni di N. Questo è anche noto come "permutazioni parziali".
La sintassi per la funzione di combinazione è - scipy.special.gamma (x). Permutazioni di N cose prese k alla volta, cioè k-permutazioni di N. Questo è anche noto come "permutazioni parziali".
from scipy.special import gamma
res = gamma([0, 0.5, 1, 5])
print resIl programma precedente genererà il seguente output.
[inf 1.77245385 1. 24.]