非決定性有限オートマトン
NDFAでは、特定の入力シンボルに対して、マシンはマシン内の状態の任意の組み合わせに移行できます。つまり、機械が移動する正確な状態を特定することはできません。したがって、それは呼ばれますNon-deterministic Automaton。状態の数が有限であるため、マシンはと呼ばれますNon-deterministic Finite Machine または Non-deterministic Finite Automaton。
NDFAの正式な定義
NDFAは、5タプル(Q、∑、δ、q 0、F)で表すことができます。
Q は有限の状態のセットです。
∑ アルファベットと呼ばれる記号の有限集合です。
δは遷移関数です。ここで、δ:Q×∑→2 Q
(ここでは、Q(2 Q)のべき集合が採用されています。これは、NDFAの場合、状態からQ状態の任意の組み合わせに遷移する可能性があるためです)
q0任意の入力が処理されるから初期状態である(Q 0 ∈Q)。
F Qの最終状態/状態のセットです(F⊆Q)。
NDFAのグラフィック表現:(DFAと同じ)
NDFAは、状態図と呼ばれる有向グラフで表されます。
- 頂点は状態を表します。
- 入力アルファベットでラベル付けされた円弧は、遷移を示します。
- 初期状態は、空の単一の入力アークによって示されます。
- 最終状態は二重丸で示されます。
Example
非決定性有限オートマトンを→
- Q = {a、b、c}
- ∑ = {0、1}
- q 0 = {a}
- F = {c}
以下に示す遷移関数δ-
| 現状 | 入力0の次の状態 | 入力1の次の状態 |
|---|---|---|
| A | a、b | b |
| b | c | 交流 |
| c | b、c | c |
そのグラフィック表現は次のようになります-
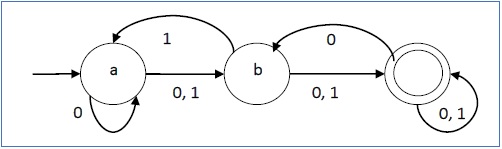
DFAとNDFA
次の表に、DFAとNDFAの違いを示します。
| DFA | NDFA |
|---|---|
| 状態からの遷移は、入力シンボルごとに1つの特定の次の状態になります。したがって、それは決定論的と呼ばれます。 | ある状態からの遷移は、入力シンボルごとに複数の次の状態になる可能性があります。したがって、それは非決定論的と呼ばれます。 |
| 空の文字列遷移はDFAでは見られません。 | NDFAは、空の文字列遷移を許可します。 |
| DFAではバックトラックが許可されています | NDFAでは、バックトラックが常に可能であるとは限りません。 |
| より多くのスペースが必要です。 | 必要なスペースが少なくて済みます。 |
| 文字列は、最終状態に移行する場合、DFAによって受け入れられます。 | すべての可能な遷移の少なくとも1つが最終状態で終了する場合、文字列はNDFAによって受け入れられます。 |
アクセプター、分類子、およびトランスデューサー
アクセプター(レコグナイザー)
ブール関数を計算するオートマトンは、 acceptor。アクセプターのすべての状態は、与えられた入力を受け入れるか拒否するかのいずれかです。
分類子
A classifier 3つ以上の最終状態があり、終了時に単一の出力を提供します。
トランスデューサー
現在の入力および/または前の状態に基づいて出力を生成するオートマトンは、 transducer。トランスデューサーには2つのタイプがあります-
Mealy Machine −出力は、現在の状態と現在の入力の両方に依存します。
Moore Machine −出力は現在の状態のみに依存します。
DFAおよびNDFAによる受容性
文字列を完全に読み取った後、初期状態で開始するDFA / NDFAが受け入れ状態(最終状態のいずれか)で終了する場合、文字列はDFA / NDFAによって受け入れられます。
文字列Sは、DFA / NDFA(Q、∑、δ、q 0、F)によって受け入れられます。
δ*(q0, S) ∈ F
言語 L DFA / NDFAによって受け入れられます
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
文字列S 'はDFA / NDFA(Q、∑、δ、q 0、F)によって受け入れられません。
δ*(q0, S′) ∉ F
DFA / NDFAによって受け入れられない言語L '(受け入れられた言語Lの補集合)は
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
Example
図1.3に示すDFAについて考えてみましょう。DFAから、許容可能な文字列を導出できます。

上記のDFAで受け入れられる文字列:{0、00、11、010、101、...........}
上記のDFAで受け入れられない文字列:{1、011、111、........}