抵抗器の回路接続
回路に接続されている場合の抵抗器。その接続は直列または並列のいずれかです。並列に接続した場合、直列に接続した場合、電流、電圧、抵抗の合計値がどうなるかを教えてください。
直列の抵抗器
直列に接続されている抵抗が少ない場合に何が起こるかを観察してみましょう。次の図に示すように、値が異なる3つの抵抗を考えてみましょう。
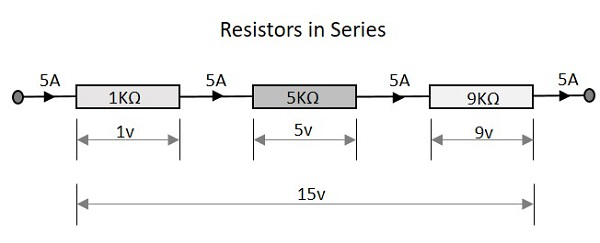
抵抗
直列抵抗を備えた回路の総抵抗は、個々の抵抗の合計に等しくなります。つまり、上の図には、それぞれ1KΩ、5KΩ、9KΩの値を持つ3つの抵抗があります。
抵抗器ネットワークの総抵抗値は−です。
$$ R \:\:= \:\:R_ {1} \:+ \:R_ {2} \:+ \:R_ {3} $$
つまり、1 + 5 + 9 =15KΩが総抵抗です。
Rここで、1は1つの抵抗である番目の抵抗は、R 2は、 2の抵抗であるND抵抗とR 3が3の抵抗であるRDの上記抵抗ネットワークにおける抵抗器。
電圧
直列抵抗ネットワークの両端に現れる合計電圧は、個々の抵抗での電圧降下の加算です。上の図には、各ステージで3つの異なる値の電圧降下を持つ3つの異なる抵抗があります。
回路の両端に現れる総電圧-
$$ V \:\:= \:\:V_ {1} \:+ \:V_ {2} \:+ \:V_ {3} $$
つまり、1v + 5v + 9v = 15vが合計電圧です。
Vここで、1は1つの電圧降下である番目の抵抗、V 2は2の電圧降下ND抵抗器及びV 3は3の電圧降下であるRDの上記抵抗ネットワークにおける抵抗器。
電流
直列に接続された抵抗器のセットを流れる電流の総量は、抵抗器ネットワーク全体のすべてのポイントで同じです。したがって、入力、抵抗間の任意のポイント、または出力で測定した場合、電流は同じ5Aになります。
ネットワークを流れる電流-
$$ I \:\:= \:\:I_ {1} \:= \:I_ {2} \:= \:I_ {3} $$
これは、すべてのポイントでの電流が5Aであることを意味します。
Iここで、1は1つのを流れる電流である番目の抵抗、I 2は2を通る電流であり、ND抵抗とI 3は3を流れる電流である番目の上記抵抗ネットワークにおける抵抗器。
並列の抵抗器
並列に接続されている抵抗が少ない場合に何が起こるかを観察してみましょう。次の図に示すように、値が異なる3つの抵抗を考えてみましょう。
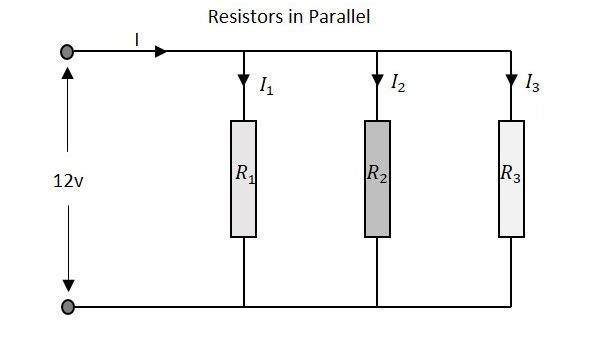
抵抗
並列抵抗を備えた回路の総抵抗は、直列抵抗ネットワーク方式とは異なる方法で計算されます。ここでは、個々の抵抗の逆数(1 / R)値に代数和の逆数を加算して、合計抵抗値を取得します。
抵抗器ネットワークの総抵抗値は−です。
$$ \ frac {1} {R} \:\:= \:\:\ frac {1} {R_ {1}} \:\:+ \:\:\ frac {1} {R_ {2}} \:\:+ \ frac {1} {R_ {3}} $$
Rここで、1は1つの抵抗である番目の抵抗は、R 2は、 2の抵抗であるND抵抗とR 3が3の抵抗であるRDの上記抵抗ネットワークにおける抵抗器。
たとえば、前の例の抵抗値を考慮すると、R 1 =1KΩ、R 2 =5KΩ、R 3 =9KΩを意味します。並列抵抗ネットワークの総抵抗は次のようになります-
$$ \ frac {1} {R} \:\:= \:\:\ frac {1} {1} \:\:+ \:\:\ frac {1} {5} \:\:+ \ frac {1} {9} $$
$$ = \:\:\ frac {45 \:\:+ \:\:9 \:\:+ \:\:5} {45} \:\:= \:\:\ frac {59} { 45} $$
$$ R \:\:= \:\:\ frac {45} {59} \:\:= \:\:0.762K \ Omega \:\:= \:\:76.2 \ Omega $$
並列抵抗の計算方法から、2抵抗並列ネットワークの簡単な式を導き出すことができます。−です
$$ R \:\:= \:\:\ frac {R_ {1} \:\:\ times \:\:R_ {2}} {R_ {1} \:\:+ \:\:R_ { 2}} \:$$
電圧
並列抵抗ネットワークの両端に現れる合計電圧は、個々の抵抗での電圧降下と同じです。
回路の両端に現れる電圧-
$$ V \:\:= \:\:V_ {1} \:= \:V_ {2} \:= \:V_ {3} $$
Vここで、1は1つの電圧降下である番目の抵抗、V 2は2の電圧降下ND抵抗器及びV 3は3の電圧降下であるRDの上記抵抗ネットワークにおける抵抗器。したがって、電圧は並列抵抗ネットワークのすべてのポイントで同じです。
電流
並列抵抗ネットワークに入る電流の合計量は、すべての並列分岐に流れるすべての個々の電流の合計です。各分岐の抵抗値によって、分岐を流れる電流の値が決まります。ネットワークを流れる総電流は
$$ I \:\:= \:\:I_ {1} \:+ \:I_ {2} \:+ \:I_ {3} $$
Iここで、1は1つのを流れる電流である番目の抵抗、I 2は2を通る電流であり、ND抵抗とI 3は3を流れる電流である番目の上記抵抗ネットワークにおける抵抗器。したがって、異なるブランチの個々の電流の合計は、並列抵抗ネットワークの合計電流を取得します。
抵抗器は、多くの回路の出力の負荷として特に使用されます。抵抗負荷をまったく使用しない場合は、負荷の前に抵抗を配置します。抵抗器は通常、どの回路でも基本的なコンポーネントです。