Pythonによる機械学習-クイックガイド
私たちは、より優れた計算能力とより多くのストレージリソースで強化された「データの時代」に生きています。このデータや情報は日々増加していますが、本当の課題はすべてのデータを理解することです。企業や組織は、データサイエンス、データマイニング、機械学習の概念と方法論を使用してインテリジェントなシステムを構築することで、これに対処しようとしています。その中で、機械学習はコンピュータサイエンスの最もエキサイティングな分野です。機械学習を、データに意味を与えるアルゴリズムのアプリケーションと科学と呼んでも間違いではありません。
機械学習とは何ですか?
機械学習(ML)は、コンピューターシステムが人間とほぼ同じ方法でデータに意味を与えることができる、コンピューターサイエンスの分野です。
簡単に言うと、MLは、アルゴリズムまたは方法を使用して生データからパターンを抽出する人工知能の一種です。MLの主な焦点は、コンピュータシステムが明示的にプログラムされたり、人間の介入を受けたりすることなく、経験から学習できるようにすることです。
機械学習の必要性
人間は、複雑な問題を考え、評価し、解決することができるため、現時点では、地球上で最も知的で先進的な種です。一方、AIはまだ初期段階にあり、多くの面で人間の知性を上回っていません。次に、問題は、機械に学習させる必要があるのかということです。これを行う最も適切な理由は、「データに基づいて、効率と規模で意思決定を行う」ことです。
最近、組織は、人工知能、機械学習、ディープラーニングなどの新しいテクノロジーに多額の投資を行って、データから重要な情報を取得し、いくつかの実際のタスクを実行して問題を解決しています。これは、特にプロセスを自動化するために、マシンによって行われるデータ主導の意思決定と呼ぶことができます。これらのデータ駆動型の決定は、プログラミングロジックを使用する代わりに、本質的にプログラムできない問題で使用できます。人間の知性がなければできないのは事実ですが、他の側面としては、現実世界の問題を大規模に効率的に解決する必要があります。そのため、機械学習が必要になります。
機械学習を行う理由と時期
機械学習の必要性についてはすでに説明しましたが、どのシナリオで機械学習を行わなければならないのかという別の疑問が生じます。データ主導の意思決定を効率的かつ大規模に行うためのマシンが必要な状況がいくつかあります。以下は、機械学習をより効果的にするような状況の一部です。
人間の専門知識の欠如
マシンにデータ主導の意思決定を学習させて実行させたい最初のシナリオは、人間の専門知識が不足しているドメインである可能性があります。例としては、未知の領域や空間惑星でのナビゲーションがあります。
動的シナリオ
本質的に動的なシナリオがいくつかあります。つまり、時間の経過とともに変化し続けます。これらのシナリオと動作の場合、マシンがデータ主導の意思決定を学習して実行する必要があります。例としては、ネットワーク接続や組織内のインフラストラクチャの可用性などがあります。
専門知識を計算タスクに変換することの難しさ
人間が専門知識を持っているさまざまな領域が存在する可能性があります。ただし、この専門知識を計算タスクに変換することはできません。このような状況では、機械学習が必要です。例としては、音声認識、認知タスクなどのドメインがあります。
機械学習モデル
機械学習モデルについて説明する前に、ミッチェル教授によって与えられたMLの次の正式な定義を理解する必要があります。
「コンピュータプログラムは、Pによって測定されたTのタスクでのパフォーマンスが、経験Eによって向上する場合、あるクラスのタスクTおよびパフォーマンス測定値Pに関して経験Eから学習すると言われています。」
上記の定義は、基本的に3つのパラメーターに焦点を当てています。また、学習アルゴリズムの主要コンポーネントであるTask(T)、Performance(P)、およびExperience(E)にも焦点を当てています。このコンテキストでは、この定義を次のように簡略化できます。
MLは、次のような学習アルゴリズムで構成されるAIの分野です。
パフォーマンスを向上させる(P)
あるタスクの実行時(T)
時間の経過とともに経験(E)
上記に基づいて、次の図は機械学習モデルを表しています-

それらについて今より詳細に議論しましょう-
タスク(T)
問題の観点から、タスクTを解決すべき現実の問題として定義することができます。問題は、特定の場所で最高の住宅価格を見つけることや、最高のマーケティング戦略を見つけることなどです。一方、機械学習について話す場合、MLベースのタスクを解決するのは難しいため、タスクの定義は異なります。従来のプログラミングアプローチ。
タスクTは、プロセスに基づいており、システムがデータポイントを操作するために従う必要がある場合、MLベースのタスクであると言われます。MLベースのタスクの例は、分類、回帰、構造化アノテーション、クラスタリング、文字起こしなどです。
経験(E)
名前が示すように、それはアルゴリズムまたはモデルに提供されるデータポイントから得られる知識です。データセットが提供されると、モデルは繰り返し実行され、いくつかの固有のパターンを学習します。このようにして得られた学習を経験(E)と呼びます。人間の学習に例えると、この状況は、人間が状況や関係などのさまざまな属性から学習または経験を積んでいる状況と考えることができます。監視付き、監視なし、強化学習は、学習または経験を積む方法の1つです。MLモデルまたはアルゴリズムから得られた経験は、タスクTを解決するために使用されます。
パフォーマンス(P)
MLアルゴリズムは、タスクを実行し、時間の経過とともに経験を積むことになっています。MLアルゴリズムが期待どおりに実行されているかどうかを判断する尺度は、そのパフォーマンス(P)です。Pは基本的に、モデルがタスクをどのように実行しているかを示す定量的メトリックTであり、その経験Eを使用します。精度スコア、F1スコア、混同行列、適合率、再現率など、MLパフォーマンスの理解に役立つ多くのメトリックがあります。 、感度など。
機械学習の課題
機械学習は急速に進化しており、サイバーセキュリティと自動運転車で大きな進歩を遂げていますが、AIのこのセグメントは、全体としてまだ長い道のりがあります。背後にある理由は、MLが多くの課題を克服できていないためです。MLが現在直面している課題は次のとおりです。
Quality of data− MLアルゴリズムの高品質なデータを持つことは、最大の課題の1つです。低品質のデータを使用すると、データの前処理と特徴抽出に関連する問題が発生します。
Time-Consuming task − MLモデルが直面するもう1つの課題は、特にデータの取得、特徴の抽出、検索にかかる時間の消費です。
Lack of specialist persons − MLテクノロジーはまだ初期段階にあるため、専門家のリソースを利用することは困難な作業です。
No clear objective for formulating business problems −このテクノロジーはまだ成熟していないため、ビジネス上の問題に対して明確な目的と明確な目標がないことは、MLのもう1つの重要な課題です。
Issue of overfitting & underfitting −モデルが過剰適合または過適合である場合、問題を適切に表すことができません。
Curse of dimensionality− MLモデルが直面するもう1つの課題は、データポイントの機能が多すぎることです。これは本当の障害になる可能性があります。
Difficulty in deployment − MLモデルは複雑であるため、実際に展開することは非常に困難です。
機械学習のアプリケーション
機械学習は最も急速に成長しているテクノロジーであり、研究者によると、私たちはAIとMLの黄金期にあります。これは、従来のアプローチでは解決できない多くの現実世界の複雑な問題を解決するために使用されます。以下は、MLの実際のアプリケーションです。
感情分析
感情分析
エラーの検出と防止
天気予報と予測
株式市場の分析と予測
音声合成
音声認識
顧客セグメンテーション
物体認識
不正検出
不正防止
オンラインショッピングにおける顧客への製品の推奨。
Pythonの紹介
Pythonは、高水準プログラミング言語の機能を備えた、人気のあるオブジェクト指向プログラミング言語です。構文と移植性を簡単に習得できるため、最近人気があります。以下の事実は私たちにPythonの紹介を与えます-
Pythonは、オランダのStichting MathematischCentrumのGuidovanRossumによって開発されました。
「ABC」というプログラミング言語の後継として書かれました。
それは1991年にリリースされた最初のバージョンです。
Pythonという名前は、MontyPythonのFlyingCircusという名前のテレビ番組からGuidovanRossumによって選ばれました。
これはオープンソースのプログラミング言語であり、自由にダウンロードしてプログラムを開発するために使用できます。www.python.orgからダウンロードできます。
Pythonプログラミング言語には、JavaとCの両方の機能があります。それはエレガントな「C」コードを持っていますが、一方で、オブジェクト指向プログラミングのためのJavaのようなクラスとオブジェクトを持っています。
これはインタープリター型言語です。つまり、Pythonプログラムのソースコードは最初にバイトコードに変換され、次にPython仮想マシンによって実行されます。
Pythonの長所と短所
すべてのプログラミング言語にはいくつかの長所と短所があり、Pythonも同様です。
強み
調査と調査によると、Pythonは5番目に重要な言語であり、機械学習とデータサイエンスで最も人気のある言語です。Pythonには次の長所があるためです-
Easy to learn and understand−Pythonの構文はより単純です。したがって、初心者でも比較的簡単に言語を学び、理解することができます。
Multi-purpose language − Pythonは、構造化プログラミング、オブジェクト指向プログラミング、および関数型プログラミングをサポートしているため、多目的プログラミング言語です。
Huge number of modules− Pythonには、プログラミングのあらゆる側面をカバーするための膨大な数のモジュールがあります。これらのモジュールは簡単に使用できるため、Pythonは拡張可能な言語になっています。
Support of open source community−オープンソースプログラミング言語であるPythonは、非常に大規模な開発者コミュニティによってサポートされています。このため、バグはPythonコミュニティによって簡単に修正されます。この特性により、Pythonは非常に堅牢で適応性があります。
Scalability − Pythonは、シェルスクリプトよりも大きなプログラムをサポートするための改善された構造を提供するため、スケーラブルなプログラミング言語です。
弱点
Pythonは人気のある強力なプログラミング言語ですが、実行速度が遅いという独自の弱点があります。
Pythonはインタープリター型言語であるため、コンパイルされた言語に比べてPythonの実行速度は遅くなります。これは、Pythonコミュニティの主要な改善領域になる可能性があります。
Pythonのインストール
Pythonで作業するには、最初にPythonをインストールする必要があります。Pythonのインストールは、次の2つの方法のいずれかで実行できます-
Pythonを個別にインストールする
事前にパッケージ化されたPythonディストリビューションの使用-Anaconda
これらについて詳しく説明します。
Pythonを個別にインストールする
コンピューターにPythonをインストールする場合は、プラットフォームに適用可能なバイナリコードのみをダウンロードする必要があります。Pythonディストリビューションは、Windows、Linux、およびMacプラットフォームで利用できます。
以下は、上記のプラットフォームへのPythonのインストールの概要です。
On Unix and Linux platform
次の手順の助けを借りて、UnixおよびLinuxプラットフォームにPythonをインストールできます-
まず、 https://www.python.org/downloads/。
次に、リンクをクリックして、Unix / Linuxで利用可能なzip形式のソースコードをダウンロードします。
次に、ファイルをダウンロードして抽出します。
次に、いくつかのオプションをカスタマイズしたい場合は、モジュール/セットアップファイルを編集できます。
次に、コマンドrun ./configurescriptを記述します
make
インストールする
On Windows platform
次の手順の助けを借りて、WindowsプラットフォームにPythonをインストールできます-
まず、 https://www.python.org/downloads/。
次に、Windowsインストーラーpython-XYZ.msiファイルのリンクをクリックします。ここでXYZはインストールしたいバージョンです。
次に、ダウンロードしたファイルを実行する必要があります。使いやすいPythonインストールウィザードが表示されます。ここで、デフォルト設定を受け入れ、インストールが完了するまで待ちます。
On Macintosh platform
Mac OS X、Homebrewの場合、Python 3をインストールするには、優れた使いやすいパッケージインストーラーをお勧めします。Homebrewをお持ちでない場合は、次のコマンドを使用してインストールできます。
$ ruby -e "$(curl -fsSL
https://raw.githubusercontent.com/Homebrew/install/master/install)"以下のコマンドで更新できます−
$ brew updateここで、Python3をシステムにインストールするには、次のコマンドを実行する必要があります-
$ brew install python3事前にパッケージ化されたPythonディストリビューションの使用:Anaconda
AnacondaはPythonのパッケージ化されたコンパイルであり、データサイエンスで広く使用されているすべてのライブラリが含まれています。次の手順に従って、Anacondaを使用してPython環境をセットアップできます-
Step1−まず、Anacondaディストリビューションから必要なインストールパッケージをダウンロードする必要があります。同じためのリンクはhttps://www.anaconda.com/distribution/。要件に応じて、Windows、Mac、およびLinuxOSから選択できます。
Step2−次に、マシンにインストールするPythonバージョンを選択します。最新のPythonバージョンは3.7です。そこでは、64ビットと32ビットの両方のグラフィカルインストーラーのオプションが表示されます。
Step3− OSとPythonのバージョンを選択すると、Anacondaインストーラーがコンピューターにダウンロードされます。ここで、ファイルをダブルクリックすると、インストーラーがAnacondaパッケージをインストールします。
Step4 −インストールされているかどうかを確認するには、コマンドプロンプトを開き、次のようにPythonと入力します。

こちらの詳細なビデオ講義でも確認できます。https://www.tutorialspoint.com/python_essentials_online_training/getting_started_with_anaconda.asp。
なぜデータサイエンスのためのPythonなのか?
Pythonは、機械学習とデータサイエンスで、5番目に重要な言語であり、最も人気のある言語です。以下は、データサイエンスの言語の優先選択となるPythonの機能です-
パッケージの豊富なセット
Pythonには、さまざまなドメインですぐに使用できる、広範で強力なパッケージのセットがあります。また、機械学習やデータサイエンスに必要な、numpy、scipy、pandas、scikit-learnなどのパッケージもあります。
簡単なプロトタイピング
データサイエンスの言語を選択できるPythonのもう1つの重要な機能は、簡単で高速なプロトタイピングです。この機能は、新しいアルゴリズムの開発に役立ちます。
コラボレーション機能
データサイエンスの分野は基本的に優れたコラボレーションを必要とし、Pythonはこれを非常に可能にする多くの便利なツールを提供します。
多くのドメインに1つの言語
典型的なデータサイエンスプロジェクトには、データ抽出、データ操作、データ分析、特徴抽出、モデリング、評価、展開、ソリューションの更新などのさまざまなドメインが含まれます。Pythonは多目的言語であるため、データサイエンティストは、共通のプラットフォームからこれらすべてのドメインに対応できます。
PythonMLエコシステムのコンポーネント
このセクションでは、Python機械学習エコシステムのコンポーネントを形成するいくつかのコアデータサイエンスライブラリについて説明します。これらの便利なコンポーネントにより、Pythonはデータサイエンスにとって重要な言語になっています。そのようなコンポーネントはたくさんありますが、ここでPythonエコシステムの重要なコンポーネントのいくつかについて説明しましょう-
Jupyter Notebook
Jupyterノートブックは基本的に、Pythonベースのデータサイエンスアプリケーションを開発するためのインタラクティブな計算環境を提供します。以前はipythonノートブックとして知られていました。以下は、PythonMLエコシステムの最高のコンポーネントの1つとなるJupyterノートブックの機能の一部です。
Jupyterノートブックは、コード、画像、テキスト、出力などを段階的に配置することで、分析プロセスを段階的に説明できます。
これは、データサイエンティストが分析プロセスを開発しながら、思考プロセスを文書化するのに役立ちます。
ノートブックの一部として結果をキャプチャすることもできます。
jupyterノートブックの助けを借りて、私たちの仕事を仲間と共有することもできます。
インストールと実行
Anacondaディストリビューションを使用している場合は、jupyterノートブックがすでにインストールされているため、個別にインストールする必要はありません。Anaconda Promptに移動し、次のコマンドを入力するだけです-
C:\>jupyter notebookEnterキーを押すと、コンピューターのlocalhost:8888でノートブックサーバーが起動します。次のスクリーンショットに示されています-

これで、[新規]タブをクリックすると、オプションのリストが表示されます。Python 3を選択すると、新しいノートブックに移動して作業を開始できます。次のスクリーンショットでそれを垣間見ることができます-


一方、標準のPythonディストリビューションを使用している場合は、人気のあるpythonパッケージインストーラーpipを使用してjupyterノートブックをインストールできます。
pip install jupyterJupyterNotebookのセルの種類
以下は、jupyterノートブックの3種類のセルです-
Code cells−名前が示すように、これらのセルを使用してコードを記述できます。コード/コンテンツを記述した後、ノートブックに関連付けられているカーネルに送信します。
Markdown cells−これらのセルを使用して計算プロセスを記録できます。テキスト、画像、ラテックス方程式、HTMLタグなどを含めることができます。
Raw cells−そこに書かれている文章はそのまま表示されます。これらのセルは基本的に、jupyternotebookの自動変換メカニズムによって変換されたくないテキストを追加するために使用されます。
jupyter Notebookの詳細については、リンクにアクセスしてください。https://www.tutorialspoint.com/jupyter/index.htm。
NumPy
これは、Pythonをデータサイエンスのお気に入りの言語の1つにするもう1つの便利なコンポーネントです。これは基本的にNumericalPythonの略で、多次元配列オブジェクトで構成されています。NumPyを使用することで、次の重要な操作を実行できます-
配列に対する数学的および論理演算。
フーリエ変換
線形代数に関連する操作。
NumPyは主にScipy(Scientific Python)およびMat-plotlib(プロットライブラリ)と一緒に使用されるため、NumPyはMatLabの代わりと見なすこともできます。
Installation and Execution
Anacondaディストリビューションを使用している場合は、NumPyが既にインストールされているため、個別にインストールする必要はありません。次の助けを借りて、Pythonスクリプトにパッケージをインポートする必要があります-
import numpy as np一方、標準のPythonディストリビューションを使用している場合は、人気のあるpythonパッケージインストーラーpipを使用してNumPyをインストールできます。
pip install NumPyNumPyの詳細については、リンクにアクセスしてください。https://www.tutorialspoint.com/numpy/index.htm。
パンダ
これは、Pythonをデータサイエンスのお気に入りの言語の1つにするもう1つの便利なPythonライブラリです。パンダは基本的にデータ操作、ラングリング、分析に使用されます。2008年にWesMcKinneyによって開発されました。Pandasの助けを借りて、データ処理で次の5つのステップを実行できます。
Load
Prepare
Manipulate
Model
Analyze
パンダでのデータ表現
パンダでのデータの表現全体は、次の3つのデータ構造の助けを借りて行われます-
Series−これは基本的に、軸ラベルが付いた1次元のndarrayであり、同種のデータを持つ単純な配列のようなものです。たとえば、次のシリーズは整数1、5、10、15、24、25のコレクションです…
| 1 | 5 | 10 | 15 | 24 | 25 | 28 | 36 | 40 | 89 |
Data frame−これは最も有用なデータ構造であり、パンダのほぼすべての種類のデータ表現と操作に使用されます。これは基本的に、異種データを含むことができる2次元のデータ構造です。一般に、表形式のデータはデータフレームを使用して表されます。たとえば、次の表は、名前とロール番号、年齢、性別を持つ学生のデータを示しています。
名前 |
ロール番号 |
年齢 |
性別 |
|---|---|---|---|
Aarav |
1 |
15 |
男性 |
ハーシット |
2 |
14 |
男性 |
カニカ |
3 |
16 |
女性 |
マヤンク |
4 |
15 |
男性 |
Panel−異種データを含む3次元データ構造です。パネルをグラフィック表現で表現することは非常に困難ですが、DataFrameのコンテナとして説明することはできます。
次の表は、パンダで使用される上記のデータ構造に関するディメンションと説明を示しています。
データ構造 |
寸法 |
説明 |
|---|---|---|
シリーズ |
1-D |
サイズ不変の1次元均質データ |
DataFrames |
2-D |
表形式のサイズ可変の異種データ |
パネル |
3-D |
サイズ可変配列、DataFrameのコンテナ。 |
高次元のデータ構造は低次元のデータ構造のコンテナであるため、これらのデータ構造を理解できます。
インストールと実行
Anacondaディストリビューションを使用している場合は、Pandasがすでにインストールされているため、個別にインストールする必要はありません。次の助けを借りて、Pythonスクリプトにパッケージをインポートする必要があります-
import pandas as pd一方、標準のPythonディストリビューションを使用している場合は、人気のあるpythonパッケージインストーラーpipを使用してPandasをインストールできます。
pip install PandasPandasをインストールした後、上記のようにPythonスクリプトにインポートできます。
例
以下は、パンダを使用してndarrayからシリーズを作成する例です。
In [1]: import pandas as pd
In [2]: import numpy as np
In [3]: data = np.array(['g','a','u','r','a','v'])
In [4]: s = pd.Series(data)
In [5]: print (s)
0 g
1 a
2 u
3 r
4 a
5 v
dtype: objectパンダのより詳細な研究については、リンクにアクセスできます https://www.tutorialspoint.com/python_pandas/index.htm。
Scikit-learn
Pythonでのデータサイエンスと機械学習に役立つもう1つの最も重要なPythonライブラリはScikit-learnです。以下は、Scikit-learnのいくつかの機能です。
これは、NumPy、SciPy、およびMatplotlib上に構築されています。
これはオープンソースであり、BSDライセンスの下で再利用できます。
誰でもアクセスでき、さまざまな状況で再利用できます。
分類、クラスタリング、回帰、次元削減、モデル選択など、MLの主要な領域をカバーする幅広い機械学習アルゴリズムを、このアルゴリズムを使用して実装できます。
インストールと実行
Anacondaディストリビューションを使用している場合は、Scikit-learnがすでにインストールされているため、個別にインストールする必要はありません。パッケージをPythonスクリプトに使用する必要があります。たとえば、次のスクリプト行を使用して、乳がん患者のデータセットをからインポートしています。Scikit-learn −
from sklearn.datasets import load_breast_cancer一方、標準のPythonディストリビューションを使用していて、NumPyとSciPyを使用している場合、Scikit-learnは一般的なPythonパッケージインストーラーpipを使用してインストールできます。
pip install -U scikit-learnScikit-learnをインストールした後、上記のようにPythonスクリプトで使用できます。
データを使用して実際の問題を解決するためのモデルを構築するために使用できるさまざまなMLアルゴリズム、手法、および方法があります。この章では、このようなさまざまな方法について説明します。
さまざまな種類の方法
以下は、いくつかの幅広いカテゴリに基づくさまざまなMLメソッドです-
人間の監督に基づく
学習過程において、人間の監督に基づくいくつかの方法は次のとおりです。
Supervised Learning
教師あり学習アルゴリズムまたは方法は、最も一般的に使用されるMLアルゴリズムです。この方法または学習アルゴリズムは、データサンプル、つまりトレーニングデータとそれに関連する出力、つまりトレーニングプロセス中の各データサンプルのラベルまたは応答を取得します。
教師あり学習アルゴリズムの主な目的は、複数のトレーニングデータインスタンスを実行した後、入力データサンプルと対応する出力の間の関連付けを学習することです。
たとえば、
x:入力変数と
Y:出力変数
ここで、アルゴリズムを適用して、入力から出力へのマッピング関数を次のように学習します。
Y = f(x)
ここで、主な目的は、新しい入力データ(x)がある場合でも、その新しい入力データの出力変数(Y)を簡単に予測できるように、マッピング関数を適切に近似することです。
教師または監督者によって監督されているので、学習のプロセス全体が考えられるため、教師ありと呼ばれます。教師あり機械学習アルゴリズムの例には、Decision tree, Random Forest, KNN, Logistic Regression 等
MLタスクに基づいて、教師あり学習アルゴリズムは次の2つの大まかなクラスに分類できます。
Classification
Regression
Classification
分類ベースのタスクの主な目的は、特定の入力データのカテゴリ出力ラベルまたは応答を予測することです。出力は、モデルがトレーニングフェーズで学習した内容に基づいています。カテゴリの出力応答は順序付けられていない離散値を意味することがわかっているため、各出力応答は特定のクラスまたはカテゴリに属します。分類と関連するアルゴリズムについては、次の章でも詳しく説明します。
Regression
回帰ベースのタスクの主な目的は、指定された入力データについて、継続的な数値である出力ラベルまたは応答を予測することです。出力は、モデルがトレーニングフェーズで学習した内容に基づいています。基本的に、回帰モデルは、入力データの特徴(独立変数)とそれに対応する連続数値出力値(従属変数または結果変数)を使用して、入力と対応する出力の間の特定の関連付けを学習します。回帰および関連するアルゴリズムについては、以降の章でも詳しく説明します。
教師なし学習
名前が示すように、教師ありMLの方法やアルゴリズムとは反対です。つまり、教師なし機械学習アルゴリズムでは、あらゆる種類のガイダンスを提供するスーパーバイザーがいません。教師なし学習アルゴリズムは、教師あり学習アルゴリズムのように、事前にラベル付けされたトレーニングデータを使用する自由がなく、入力データから有用なパターンを抽出したい場合に便利です。
たとえば、次のように理解できます。
私たちが持っていると仮定します-
x: Input variablesの場合、対応する出力変数はなく、アルゴリズムは学習のためにデータ内の興味深いパターンを検出する必要があります。
教師なし機械学習アルゴリズムの例には、K-meansクラスタリングが含まれます。 K-nearest neighbors 等
MLタスクに基づいて、教師なし学習アルゴリズムは次の幅広いクラスに分類できます-
Clustering
Association
次元削減
Clustering
クラスタリング手法は、最も有用な教師なしML手法の1つです。これらのアルゴリズムは、データサンプル間の類似性と関係パターンを見つけ、それらのサンプルを特徴に基づいて類似性を持つグループにクラスター化するために使用されました。クラスタリングの実際の例は、購入行動によって顧客をグループ化することです。
Association
もう1つの有用な教師なしMLメソッドは Associationこれは、大規模なデータセットを分析して、さまざまなアイテム間の興味深い関係をさらに表すパターンを見つけるために使用されます。とも呼ばれますAssociation Rule Mining または Market basket analysis これは主に顧客の買い物パターンを分析するために使用されます。
Dimensionality Reduction
この教師なしML法は、主要な特徴または代表的な特徴のセットを選択することにより、各データサンプルの特徴変数の数を減らすために使用されます。ここで疑問が生じるのは、なぜ次元を減らす必要があるのかということです。背後にある理由は、データサンプルから数百万の特徴を分析および抽出し始めるときに発生する特徴空間の複雑さの問題です。この問題は一般的に「次元の呪い」を指します。PCA(主成分分析)、K最近傍分析、判別分析は、この目的でよく使用されるアルゴリズムの一部です。
Anomaly Detection
この教師なしMLメソッドは、通常は発生しないまれなイベントまたは観測の発生を見つけるために使用されます。学習した知識を使用することにより、異常検出方法は異常なデータポイントと正常なデータポイントを区別することができます。クラスタリングなどの教師なしアルゴリズムの一部であるKNNは、データとその機能に基づいて異常を検出できます。
半教師あり学習
このような種類のアルゴリズムまたはメソッドは、完全に監視されているわけでも、完全に監視されていないわけでもありません。それらは基本的に2つ、つまり教師あり学習方法と教師なし学習方法の間にあります。これらの種類のアルゴリズムは、一般に、小さな教師あり学習コンポーネント、つまり、事前にラベル付けされた少量の注釈付きデータと、大きな教師なし学習コンポーネント、つまり、トレーニング用の多くのラベルなしデータを使用します。半教師あり学習方法を実装するには、次のいずれかのアプローチに従うことができます。
最初の簡単なアプローチは、少量のラベル付きおよび注釈付きデータに基づいて教師ありモデルを構築し、次にそれを大量のラベルなしデータに適用してより多くのラベル付きサンプルを取得することにより、教師なしモデルを構築することです。次に、それらでモデルをトレーニングし、プロセスを繰り返します。
- 、p> 2番目のアプローチには、追加の作業が必要です。このアプローチでは、最初に教師なしメソッドを使用して類似のデータサンプルをクラスター化し、これらのグループに注釈を付けてから、この情報の組み合わせを使用してモデルをトレーニングできます。
強化学習
これらの方法は、以前に研究された方法とは異なり、非常にまれにしか使用されません。この種の学習アルゴリズムでは、特定の環境と相互作用できるように、一定期間にわたってトレーニングしたいエージェントが存在します。エージェントは、環境と対話するための一連の戦略に従い、環境を観察した後、環境の現在の状態に関してアクションを実行します。以下は強化学習法の主なステップです-
Step1 −最初に、いくつかの初期戦略セットを備えたエージェントを準備する必要があります。
Step2 −次に、環境とその現在の状態を観察します。
Step3 −次に、環境の現状に応じて最適なポリシーを選択し、重要なアクションを実行します。
Step4 −これで、エージェントは、前のステップで実行したアクションに従って、対応する報酬またはペナルティを取得できます。
Step5 −必要に応じて、戦略を更新できるようになりました。
Step6 −最後に、エージェントが最適なポリシーを学習して採用するまで、手順2〜5を繰り返します。
機械学習に適したタスク
次の図は、さまざまなML問題に適したタスクのタイプを示しています-

学習能力に基づく
学習過程において、以下は学習能力に基づくいくつかの方法です-
Batch Learning
多くの場合、利用可能なトレーニングデータ全体を使用してモデルを一度にトレーニングする必要があるエンドツーエンドの機械学習システムがあります。このような学習方法やアルゴリズムは、Batch or Offline learning。これは1回限りの手順であり、モデルが1つのバッチでデータを使用してトレーニングされるため、バッチ学習またはオフライン学習と呼ばれます。バッチ学習方法の主な手順は次のとおりです-
Step1 −まず、モデルのトレーニングを開始するために、すべてのトレーニングデータを収集する必要があります。
Step2 −次に、トレーニングデータ全体を一度に提供して、モデルのトレーニングを開始します。
Step3 −次に、満足のいく結果/パフォーマンスが得られたら、学習/トレーニングプロセスを停止します。
Step4−最後に、このトレーニング済みモデルを本番環境にデプロイします。ここでは、新しいデータサンプルの出力を予測します。
オンライン学習
これは、バッチまたはオフラインの学習方法とは完全に反対です。これらの学習方法では、トレーニングデータは、ミニバッチと呼ばれる複数の増分バッチでアルゴリズムに提供されます。以下は、オンライン学習方法の主なステップです-
Step1 −まず、モデルのトレーニングを開始するために、すべてのトレーニングデータを収集する必要があります。
Step2 −次に、アルゴリズムにトレーニングデータのミニバッチを提供して、モデルのトレーニングを開始します。
Step3 −次に、トレーニングデータのミニバッチを複数の増分でアルゴリズムに提供する必要があります。
Step4 −バッチ学習のように停止しないため、ミニバッチでトレーニングデータ全体を提供した後、新しいデータサンプルも提供します。
Step5 −最後に、新しいデータサンプルに基づいて一定期間学習を続けます。
一般化アプローチに基づく
学習プロセスにおいて、以下は一般化アプローチに基づくいくつかの方法です-
インスタンスベースの学習
インスタンスベースの学習方法は、入力データに基づいて一般化を行うことでMLモデルを構築する便利な方法の1つです。この種の学習にはMLシステムや、トレーニングデータに明示的なモデルを構築せずに、生データポイント自体を使用して新しいデータサンプルの結果を描画する方法が含まれるという点で、以前に学習した学習方法とは逆です。
簡単に言うと、インスタンスベースの学習は基本的に、入力データポイントを確認することから始まり、類似性メトリックを使用して、新しいデータポイントを一般化して予測します。
モデルベースの学習
モデルベースの学習方法では、ハイパーパラメータと呼ばれるさまざまなモデルパラメータに基づいて構築され、入力データを使用して特徴を抽出するMLモデルで反復プロセスが実行されます。この学習では、ハイパーパラメータはさまざまなモデル検証手法に基づいて最適化されます。そのため、モデルベースの学習方法では、一般化に向けてより伝統的なMLアプローチを使用していると言えます。
MLプロジェクトを開始したい場合、最初に必要な最も重要なことは何ですか?これは、MLプロジェクトを開始するためにロードする必要のあるデータです。データに関して、MLプロジェクトのデータの最も一般的な形式はCSV(コンマ区切り値)です。
基本的に、CSVは、スプレッドシートなどの表形式のデータ(数値とテキスト)をプレーンテキストで保存するために使用される単純なファイル形式です。Pythonでは、さまざまな方法でCSVデータを読み込むことができますが、CSVデータを読み込む前に、いくつかの考慮事項に注意する必要があります。
CSVデータの読み込み時の考慮事項
CSVデータ形式はMLデータの最も一般的な形式ですが、MLプロジェクトに同じものを読み込む際には、次の主要な考慮事項に注意する必要があります。
ファイルヘッダー
CSVデータファイルでは、ヘッダーに各フィールドの情報が含まれています。データフィールドの解釈方法を指定するのはヘッダーファイルであるため、ヘッダーファイルとデータファイルに同じ区切り文字を使用する必要があります。
以下は、考慮しなければならないCSVファイルヘッダーに関連する2つのケースです-
Case-I: When Data file is having a file header −データファイルにファイルヘッダーがある場合は、データの各列に名前が自動的に割り当てられます。
Case-II: When Data file is not having a file header −データファイルにファイルヘッダーがない場合は、データの各列に手動で名前を割り当てる必要があります。
どちらの場合も、CSVファイルにヘッダーが含まれているかどうかを明示的に指定する必要があります。
コメント
データファイル内のコメントには、その重要性があります。CSVデータファイルでは、コメントは行頭にハッシュ(#)で示されます。ファイルにコメントがある場合は、ロードするために選択した方法に応じて、それらのコメントを予期するかどうかを示す必要があるため、CSVデータをMLプロジェクトにロードするときにコメントを考慮する必要があります。
デリミタ
CSVデータファイルでは、コンマ(、)文字が標準の区切り文字です。区切り文字の役割は、フィールドの値を区切ることです。タブや空白などの別の区切り文字を使用することもできるため、CSVファイルをMLプロジェクトにアップロードする際に区切り文字の役割を考慮することが重要です。ただし、標準の区切り文字とは異なる区切り文字を使用する場合は、明示的に指定する必要があります。
引用
CSVデータファイルでは、二重引用符(“”)マークがデフォルトの引用符です。二重引用符以外の引用符を使用することもできるため、CSVファイルをMLプロジェクトにアップロードする際には、引用符の役割を考慮することが重要です。ただし、標準とは異なる引用符を使用する場合は、明示的に指定する必要があります。
CSVデータファイルをロードする方法
MLプロジェクトで作業する場合、最も重要なタスクはデータを適切にロードすることです。MLプロジェクトの最も一般的なデータ形式はCSVであり、さまざまなフレーバーとさまざまな解析の難しさがあります。このセクションでは、CSVデータファイルをロードするためのPythonの3つの一般的なアプローチについて説明します。
Python標準ライブラリでCSVをロードする
CSVデータファイルをロードするための最初で最も使用されているアプローチは、さまざまな組み込みモジュール、つまりcsvモジュールとreader()関数を提供するPython標準ライブラリの使用です。以下は、CSVデータファイルを使用してロードする例です-
例
この例では、ローカルディレクトリにダウンロードできるアイリスフラワーデータセットを使用しています。データファイルを読み込んだ後、それをNumPy配列に変換して、MLプロジェクトに使用できます。以下は、CSVデータファイルをロードするためのPythonスクリプトです-
まず、Python標準ライブラリが提供するcsvモジュールを次のようにインポートする必要があります-
import csv次に、ロードされたデータをNumPy配列に変換するためのNumpyモジュールをインポートする必要があります。
import numpy as npここで、CSVデータファイルを含む、ローカルディレクトリに保存されているファイルのフルパスを指定します-
path = r"c:\iris.csv"次に、csv.reader()関数を使用してCSVファイルからデータを読み取ります-
with open(path,'r') as f:
reader = csv.reader(f,delimiter = ',')
headers = next(reader)
data = list(reader)
data = np.array(data).astype(float)次のスクリプト行を使用して、ヘッダーの名前を出力できます-
print(headers)次のスクリプト行は、データの形状、つまりファイル内の行と列の数を出力します-
print(data.shape)次のスクリプト行は、データファイルの最初の3行を示します-
print(data[:3])Output
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
(150, 4)
[ [5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]]NumPyでCSVを読み込む
CSVデータファイルをロードする別のアプローチは、NumPyおよびnumpy.loadtxt()関数です。以下は、CSVデータファイルを使用してロードする例です-
例
この例では、糖尿病患者のデータを持つPima IndiansDatasetを使用しています。このデータセットは、ヘッダーのない数値データセットです。ローカルディレクトリにダウンロードすることもできます。データファイルを読み込んだ後、それをNumPy配列に変換して、MLプロジェクトに使用できます。以下は、CSVデータファイルをロードするためのPythonスクリプトです-
from numpy import loadtxt
path = r"C:\pima-indians-diabetes.csv"
datapath= open(path, 'r')
data = loadtxt(datapath, delimiter=",")
print(data.shape)
print(data[:3])出力
(768, 9)
[ [ 6. 148. 72. 35. 0. 33.6 0.627 50. 1.]
[ 1. 85. 66. 29. 0. 26.6 0.351 31. 0.]
[ 8. 183. 64. 0. 0. 23.3 0.672 32. 1.]]パンダでCSVを読み込む
CSVデータファイルをロードする別のアプローチは、Pandasとpandas.read_csv()関数によるものです。これは、プロットにすぐに使用できるpandas.DataFrameを返す非常に柔軟な関数です。以下は、CSVデータファイルを使用してロードする例です-
例
ここでは、2つのPythonスクリプトを実装します。1つはヘッダーのあるIrisデータセットを使用するもので、もう1つはヘッダーのない数値データセットであるPima IndiansDatasetを使用するものです。両方のデータセットをローカルディレクトリにダウンロードできます。
Script-1
以下は、アイリスデータセットでパンダを使用してCSVデータファイルをロードするためのPythonスクリプトです-
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.shape)
print(data[:3])
Output:
(150, 4)
sepal_length sepal_width petal_length petal_width
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2Script-2
以下は、CSVデータファイルをロードするためのPythonスクリプトであり、ヘッダー名も提供します。PimaIndiansDiabetesデータセットでPandasを使用します-
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
print(data.shape)
print(data[:3])Output
(768, 9)
preg plas pres skin test mass pedi age class
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1CSVデータファイルをロードするために使用された上記の3つのアプローチの違いは、与えられた例の助けを借りて簡単に理解することができます。
前書き
機械学習プロジェクトで作業している間、通常、次の2つの最も重要な部分を無視します。 mathematics そして data。MLはデータ駆動型のアプローチであり、MLモデルは、提供したデータと同じくらい良い結果または悪い結果しか生成しないことがわかっているためです。
前の章では、CSVデータをMLプロジェクトにアップロードする方法について説明しましたが、アップロードする前にデータを理解しておくとよいでしょう。データは、統計と視覚化の2つの方法で理解できます。
この章では、次のPythonレシピを使用して、統計を使用してMLデータを理解します。
生データを見る
最初のレシピは、生データを確認するためのものです。生データを見た後に得られる洞察は、MLプロジェクトのデータの処理だけでなく、より良い前処理の可能性を高めるため、生データを見ることが重要です。
以下は、ピマインディアンの糖尿病データセットでPandas DataFrameのhead()関数を使用して実装されたPythonスクリプトで、最初の50行を調べて理解を深めます。
例
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
print(data.head(50))出力
preg plas pres skin test mass pedi age class
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1
5 5 116 74 0 0 25.6 0.201 30 0
6 3 78 50 32 88 31.0 0.248 26 1
7 10 115 0 0 0 35.3 0.134 29 0
8 2 197 70 45 543 30.5 0.158 53 1
9 8 125 96 0 0 0.0 0.232 54 1
10 4 110 92 0 0 37.6 0.191 30 0
11 10 168 74 0 0 38.0 0.537 34 1
12 10 139 80 0 0 27.1 1.441 57 0
13 1 189 60 23 846 30.1 0.398 59 1
14 5 166 72 19 175 25.8 0.587 51 1
15 7 100 0 0 0 30.0 0.484 32 1
16 0 118 84 47 230 45.8 0.551 31 1
17 7 107 74 0 0 29.6 0.254 31 1
18 1 103 30 38 83 43.3 0.183 33 0
19 1 115 70 30 96 34.6 0.529 32 1
20 3 126 88 41 235 39.3 0.704 27 0
21 8 99 84 0 0 35.4 0.388 50 0
22 7 196 90 0 0 39.8 0.451 41 1
23 9 119 80 35 0 29.0 0.263 29 1
24 11 143 94 33 146 36.6 0.254 51 1
25 10 125 70 26 115 31.1 0.205 41 1
26 7 147 76 0 0 39.4 0.257 43 1
27 1 97 66 15 140 23.2 0.487 22 0
28 13 145 82 19 110 22.2 0.245 57 0
29 5 117 92 0 0 34.1 0.337 38 0
30 5 109 75 26 0 36.0 0.546 60 0
31 3 158 76 36 245 31.6 0.851 28 1
32 3 88 58 11 54 24.8 0.267 22 0
33 6 92 92 0 0 19.9 0.188 28 0
34 10 122 78 31 0 27.6 0.512 45 0
35 4 103 60 33 192 24.0 0.966 33 0
36 11 138 76 0 0 33.2 0.420 35 0
37 9 102 76 37 0 32.9 0.665 46 1
38 2 90 68 42 0 38.2 0.503 27 1
39 4 111 72 47 207 37.1 1.390 56 1
40 3 180 64 25 70 34.0 0.271 26 0
41 7 133 84 0 0 40.2 0.696 37 0
42 7 106 92 18 0 22.7 0.235 48 0
43 9 171 110 24 240 45.4 0.721 54 1
44 7 159 64 0 0 27.4 0.294 40 0
45 0 180 66 39 0 42.0 1.893 25 1
46 1 146 56 0 0 29.7 0.564 29 0
47 2 71 70 27 0 28.0 0.586 22 0
48 7 103 66 32 0 39.1 0.344 31 1
49 7 105 0 0 0 0.0 0.305 24 0上記の出力から、最初の列が特定の観測値を参照するのに非常に役立つ行番号を示していることがわかります。
データの次元の確認
MLプロジェクト用に、行と列の観点からどれだけのデータがあるかを知ることは常に良い習慣です。背後にある理由は-
行と列が多すぎる場合、アルゴリズムの実行とモデルのトレーニングに長い時間がかかると仮定します。
行と列が少なすぎると、モデルを適切にトレーニングするのに十分なデータがないとします。
以下は、Pandasデータフレームにshapeプロパティを出力することによって実装されたPythonスクリプトです。行と列の総数を取得するために、アイリスデータセットに実装します。
例
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.shape)出力
(150, 4)出力から、使用するアイリスデータセットが150行4列であることが簡単にわかります。
各属性のデータ型の取得
各属性のデータ型を知ることは、もう1つの良い習慣です。背後にある理由は、要件に従って、あるデータ型を別のデータ型に変換する必要がある場合があるためです。たとえば、カテゴリ値または順序値を表すために、文字列を浮動小数点またはintに変換する必要がある場合があります。生データを見ることで属性のデータ型を知ることができますが、別の方法はPandasDataFrameのdtypesプロパティを使用することです。dtypesプロパティを使用して、各属性のデータ型を分類できます。次のPythonスクリプトの助けを借りて理解することができます-
例
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.dtypes)出力
sepal_length float64
sepal_width float64
petal_length float64
petal_width float64
dtype: object上記の出力から、各属性のデータ型を簡単に取得できます。
データの統計的要約
データの形状、つまり行と列の数を取得するためのPythonレシピについて説明しましたが、多くの場合、その形状のデータから要約を確認する必要があります。これは、Pandas DataFrameのdescribe()関数を使用して実行できます。この関数は、すべてのデータ属性の次の8つの統計プロパティをさらに提供します。
Count
Mean
標準偏差
最小値
最大値
25%
中央値すなわち50%
75%
例
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
print(data.shape)
print(data.describe())出力
(768, 9)
preg plas pres skin test mass pedi age class
count 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00
mean 3.85 120.89 69.11 20.54 79.80 31.99 0.47 33.24 0.35
std 3.37 31.97 19.36 15.95 115.24 7.88 0.33 11.76 0.48
min 0.00 0.00 0.00 0.00 0.00 0.00 0.08 21.00 0.00
25% 1.00 99.00 62.00 0.00 0.00 27.30 0.24 24.00 0.00
50% 3.00 117.00 72.00 23.00 30.50 32.00 0.37 29.00 0.00
75% 6.00 140.25 80.00 32.00 127.25 36.60 0.63 41.00 1.00
max 17.00 199.00 122.00 99.00 846.00 67.10 2.42 81.00 1.00上記の出力から、ピマインディアン糖尿病データセットのデータの統計的要約とデータの形状を観察できます。
クラス分布の確認
クラス分布統計は、クラス値のバランスを知る必要がある分類問題で役立ちます。クラス値の分布を知ることは重要です。なぜなら、クラスの分布が非常に不均衡である場合、つまり1つのクラスが他のクラスよりも多くの観測値を持っている場合、MLプロジェクトのデータ準備段階で特別な処理が必要になる可能性があるためです。Pandas DataFrameを使用すると、Pythonでクラス配布を簡単に取得できます。
例
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
count_class = data.groupby('class').size()
print(count_class)出力
Class
0 500
1 268
dtype: int64上記の出力から、クラス0の観測数はクラス1の観測数のほぼ2倍であることがはっきりとわかります。
属性間の相関関係の確認
2つの変数間の関係は相関と呼ばれます。統計では、相関を計算するための最も一般的な方法はピアソンの相関係数です。次の3つの値を持つことができます-
Coefficient value = 1 −それは完全を表します positive 変数間の相関。
Coefficient value = -1 −それは完全を表します negative 変数間の相関。
Coefficient value = 0 −それは no 変数間の相関関係。
MLプロジェクトで使用する前に、データセット内の属性のペアワイズ相関を確認することは常に良いことです。相関の高い属性がある場合、線形回帰やロジスティック回帰などの一部の機械学習アルゴリズムのパフォーマンスが低下するためです。Pythonでは、Pandas DataFrameのcorr()関数を使用して、データセット属性の相関行列を簡単に計算できます。
例
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
correlations = data.corr(method='pearson')
print(correlations)出力
preg plas pres skin test mass pedi age class
preg 1.00 0.13 0.14 -0.08 -0.07 0.02 -0.03 0.54 0.22
plas 0.13 1.00 0.15 0.06 0.33 0.22 0.14 0.26 0.47
pres 0.14 0.15 1.00 0.21 0.09 0.28 0.04 0.24 0.07
skin -0.08 0.06 0.21 1.00 0.44 0.39 0.18 -0.11 0.07
test -0.07 0.33 0.09 0.44 1.00 0.20 0.19 -0.04 0.13
mass 0.02 0.22 0.28 0.39 0.20 1.00 0.14 0.04 0.29
pedi -0.03 0.14 0.04 0.18 0.19 0.14 1.00 0.03 0.17
age 0.54 0.26 0.24 -0.11 -0.04 0.04 0.03 1.00 0.24
class 0.22 0.47 0.07 0.07 0.13 0.29 0.17 0.24 1.00上記の出力のマトリックスは、データセット内の属性のすべてのペア間の相関関係を示しています。
属性分布のスキューの確認
歪度は、ガウス分布であると想定されているが、歪んでいるか、ある方向または別の方向に、あるいは左または右にシフトしているように見える分布として定義できます。属性の歪度を確認することは、次の理由により重要なタスクの1つです-
データに歪度が存在する場合は、モデルからより正確に取得できるように、データ準備段階で修正する必要があります。
ほとんどのMLアルゴリズムは、データがガウス分布、つまりベルカーブデータの正規分布を持っていることを前提としています。
Pythonでは、Pandas DataFrameのskew()関数を使用して、各属性のスキューを簡単に計算できます。
例
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
print(data.skew())出力
preg 0.90
plas 0.17
pres -1.84
skin 0.11
test 2.27
mass -0.43
pedi 1.92
age 1.13
class 0.64
dtype: float64上記の出力から、正または負のスキューが観察されます。値がゼロに近い場合、スキューが少なくなります。
前書き
前の章では、統計を使用してデータを理解するためのいくつかのPythonレシピとともに、機械学習アルゴリズムのデータの重要性について説明しました。データを理解するために、視覚化と呼ばれる別の方法があります。
データの視覚化の助けを借りて、データがどのように見えるか、およびデータの属性によってどのような相関関係が保持されているかを確認できます。これは、機能が出力に対応しているかどうかを確認するための最速の方法です。次のPythonレシピの助けを借りて、統計を使用してMLデータを理解できます。

単変量プロット:属性を独立して理解する
最も単純なタイプの視覚化は、単一変数または「単変量」の視覚化です。単変量の視覚化の助けを借りて、データセットの各属性を個別に理解できます。以下は、単変量の視覚化を実装するためのPythonのいくつかの手法です-
ヒストグラム
ヒストグラムはデータをビンにグループ化し、データセット内の各属性の分布についてのアイデアを得る最も速い方法です。以下はヒストグラムの特徴の一部です-
これは、視覚化のために作成された各ビン内の観測数のカウントを提供します。
ビンの形状から、分布、つまり、ガウス分布、歪曲、または指数関数的な天気を簡単に観察できます。
ヒストグラムは、外れ値の可能性を確認するのにも役立ちます。
例
以下に示すコードは、Pima IndianDiabetesデータセットの属性のヒストグラムを作成するPythonスクリプトの例です。ここでは、Pandas DataFrameでhist()関数を使用して、ヒストグラムを生成します。matplotlib それらをプロットするため。
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.hist()
pyplot.show()出力
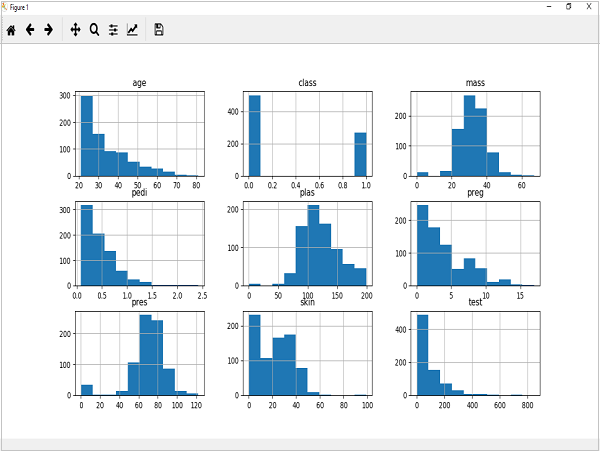
上記の出力は、データセット内の各属性のヒストグラムを作成したことを示しています。このことから、おそらく年齢、ペディ、テスト属性は指数分布であるのに対し、質量とプラはガウス分布であることがわかります。
密度プロット
各属性の分布を取得するためのもう1つのすばやく簡単な手法は、密度プロットです。これもヒストグラムに似ていますが、各ビンの上部から滑らかな曲線が描かれています。それらを抽象化されたヒストグラムと呼ぶことができます。
例
次の例では、Pythonスクリプトは、Pima IndianDiabetesデータセットの属性の分布の密度プロットを生成します。
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.plot(kind='density', subplots=True, layout=(3,3), sharex=False)
pyplot.show()出力
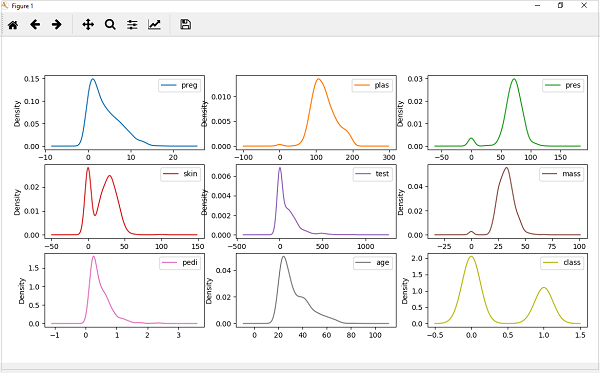
上記の出力から、密度プロットとヒストグラムの違いを簡単に理解できます。
箱ひげ図
箱ひげ図とも呼ばれる箱ひげ図は、各属性の分布を確認するためのもう1つの便利な手法です。この手法の特徴は次のとおりです。
それは本質的に単変量であり、各属性の分布を要約します。
中央値、つまり中央値に線を引きます。
25%と75%の周りにボックスを描画します。
また、データの広がりについてのアイデアを与えるひげを描きます。
ひげの外側の点は、外れ値を示します。外れ値は、中間データの広がりのサイズの1.5倍になります。
例
次の例では、Pythonスクリプトは、Pima IndianDiabetesデータセットの属性の分布の密度プロットを生成します。
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.plot(kind='box', subplots=True, layout=(3,3), sharex=False,sharey=False)
pyplot.show()出力

上記の属性の分布のプロットから、年齢、テスト、および肌が小さい値に向かって歪んでいるように見えることがわかります。
多変量プロット:複数の変数間の交互作用
別のタイプの視覚化は、多変数または「多変量」視覚化です。多変量視覚化の助けを借りて、データセットの複数の属性間の相互作用を理解できます。以下は、多変量視覚化を実装するためのPythonのいくつかの手法です-
相関行列プロット
相関は、2つの変数間の変化についての指標です。前の章では、ピアソンの相関係数と相関の重要性についても説明しました。相関行列をプロットして、どの変数が別の変数に関して高い相関または低い相関を持っているかを示すことができます。
例
次の例では、PythonスクリプトがPima IndianDiabetesデータセットの相関行列を生成してプロットします。これは、Pandas DataFrameのcorr()関数を使用して生成し、pyplotを使用してプロットできます。
from matplotlib import pyplot
from pandas import read_csv
import numpy
Path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(Path, names=names)
correlations = data.corr()
fig = pyplot.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(correlations, vmin=-1, vmax=1)
fig.colorbar(cax)
ticks = numpy.arange(0,9,1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
pyplot.show()出力

上記の相関行列の出力から、対称であることがわかります。つまり、左下が右上と同じです。また、各変数が互いに正の相関関係にあることも確認されています。
散布行列プロット
散布図は、2次元のドットを使用して、ある変数が別の変数によってどの程度影響を受けるか、またはそれらの間の関係を示します。散布図は、水平軸と垂直軸を使用してデータポイントをプロットするという概念では、折れ線グラフに非常によく似ています。
例
次の例では、PythonスクリプトがPima IndianDiabetesデータセットの散布行列を生成してプロットします。これは、Pandas DataFrameのscatter_matrix()関数を使用して生成し、pyplotを使用してプロットできます。
from matplotlib import pyplot
from pandas import read_csv
from pandas.tools.plotting import scatter_matrix
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
scatter_matrix(data)
pyplot.show()出力

前書き
機械学習アルゴリズムは、モデルトレーニングを可能にする最も重要な側面であるため、データに完全に依存しています。一方、そのデータを理解できない場合は、MLアルゴリズムにデータを供給する前に、マシンは役に立たなくなります。簡単に言えば、マシンに解決させたい問題に対して、常に正しいデータ、つまり正しいスケール、フォーマット、意味のある機能を含むデータを提供する必要があります。
これにより、データの準備がMLプロセスの最も重要なステップになります。データの準備は、データセットをMLプロセスにより適したものにする手順として定義できます。
なぜデータ前処理?
MLトレーニング用の生データを選択した後、最も重要なタスクはデータの前処理です。広い意味で、データ前処理は、選択されたデータを、使用できる形式またはMLアルゴリズムにフィードできる形式に変換します。機械学習アルゴリズムの期待どおりになるように、常にデータを前処理する必要があります。
データ前処理技術
MLアルゴリズムのデータを生成するためにデータセットに適用できる次のデータ前処理技術があります-
スケーリング
ほとんどの場合、データセットはさまざまなスケールの属性で構成されていますが、そのようなデータをMLアルゴリズムに提供できないため、再スケーリングが必要です。データの再スケーリングにより、属性が同じスケールになるようになります。通常、属性は0から1の範囲に再スケーリングされます。勾配降下法やk最近傍法などのMLアルゴリズムには、スケーリングされたデータが必要です。scikit-learnPythonライブラリのMinMaxScalerクラスを使用してデータを再スケーリングできます。
例
この例では、以前に使用したPima IndiansDiabetesデータセットのデータを再スケーリングします。最初に、CSVデータがロードされ(前の章で行われたように)、次にMinMaxScalerクラスの助けを借りて、0から1の範囲で再スケーリングされます。
次のスクリプトの最初の数行は、CSVデータの読み込み中に前の章で記述したものと同じです。
from pandas import read_csv
from numpy import set_printoptions
from sklearn import preprocessing
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesこれで、MinMaxScalerクラスを使用して、0から1の範囲でデータを再スケーリングできます。
data_scaler = preprocessing.MinMaxScaler(feature_range=(0,1))
data_rescaled = data_scaler.fit_transform(array)選択に応じて、出力用のデータを要約することもできます。ここでは、精度を1に設定し、出力の最初の10行を表示しています。
set_printoptions(precision=1)
print ("\nScaled data:\n", data_rescaled[0:10])出力
Scaled data:
[[0.4 0.7 0.6 0.4 0. 0.5 0.2 0.5 1. ]
[0.1 0.4 0.5 0.3 0. 0.4 0.1 0.2 0. ]
[0.5 0.9 0.5 0. 0. 0.3 0.3 0.2 1. ]
[0.1 0.4 0.5 0.2 0.1 0.4 0. 0. 0. ]
[0. 0.7 0.3 0.4 0.2 0.6 0.9 0.2 1. ]
[0.3 0.6 0.6 0. 0. 0.4 0.1 0.2 0. ]
[0.2 0.4 0.4 0.3 0.1 0.5 0.1 0.1 1. ]
[0.6 0.6 0. 0. 0. 0.5 0. 0.1 0. ]
[0.1 1. 0.6 0.5 0.6 0.5 0. 0.5 1. ]
[0.5 0.6 0.8 0. 0. 0. 0.1 0.6 1. ]]上記の出力から、すべてのデータが0から1の範囲に再スケーリングされました。
正規化
もう1つの有用なデータ前処理手法は、正規化です。これは、データの各行を1の長さに再スケーリングするために使用されます。これは主に、ゼロがたくさんあるスパースデータセットで役立ちます。scikit-learnPythonライブラリのNormalizerクラスを使用してデータを再スケーリングできます。
正規化の種類
機械学習では、次の2種類の正規化前処理手法があります。
L1正規化
これは、各行で絶対値の合計が常に最大1になるようにデータセット値を変更する正規化手法として定義できます。これは、最小絶対偏差とも呼ばれます。
Example
この例では、L1正規化手法を使用して、以前に使用したPima IndiansDiabetesデータセットのデータを正規化します。最初にCSVデータが読み込まれ、次にNormalizerクラスを使用して正規化されます。
次のスクリプトの最初の数行は、CSVデータの読み込み中に前の章で記述したものと同じです。
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv (path, names=names)
array = dataframe.valuesこれで、L1でNormalizerクラスを使用して、データを正規化できます。
Data_normalizer = Normalizer(norm='l1').fit(array)
Data_normalized = Data_normalizer.transform(array)選択に応じて、出力用のデータを要約することもできます。ここでは、精度を2に設定し、出力の最初の3行を表示しています。
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])Output
Normalized data:
[[0.02 0.43 0.21 0.1 0. 0.1 0. 0.14 0. ]
[0. 0.36 0.28 0.12 0. 0.11 0. 0.13 0. ]
[0.03 0.59 0.21 0. 0. 0.07 0. 0.1 0. ]]L2正規化
これは、各行で二乗の合計が常に最大1になるようにデータセット値を変更する正規化手法として定義できます。これは最小二乗とも呼ばれます。
Example
この例では、L2正規化手法を使用して、以前に使用したPima IndiansDiabetesデータセットのデータを正規化します。最初に、CSVデータがロードされ(前の章で行われたように)、次にNormalizerクラスの助けを借りて正規化されます。
次のスクリプトの最初の数行は、CSVデータの読み込み中に前の章で記述したものと同じです。
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv (path, names=names)
array = dataframe.valuesこれで、L1でNormalizerクラスを使用して、データを正規化できます。
Data_normalizer = Normalizer(norm='l2').fit(array)
Data_normalized = Data_normalizer.transform(array)選択に応じて、出力用のデータを要約することもできます。ここでは、精度を2に設定し、出力の最初の3行を表示しています。
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])Output
Normalized data:
[[0.03 0.83 0.4 0.2 0. 0.19 0. 0.28 0.01]
[0.01 0.72 0.56 0.24 0. 0.22 0. 0.26 0. ]
[0.04 0.92 0.32 0. 0. 0.12 0. 0.16 0.01]]二値化
名前が示すように、これはデータをバイナリにするための手法です。データをバイナリにするために、バイナリしきい値を使用できます。そのしきい値を超える値は1に変換され、そのしきい値を下回る値は0に変換されます。たとえば、しきい値= 0.5を選択すると、それより上のデータセット値は1になり、これより下のデータセット値は0になります。なぜそれを呼ぶことができるのかbinarizing データまたは thresholdingデータ。この手法は、データセットに確率があり、それらを鮮明な値に変換する場合に役立ちます。
scikit-learnPythonライブラリのBinarizerクラスを使用してデータを2値化できます。
例
この例では、以前に使用したPima IndiansDiabetesデータセットのデータを再スケーリングします。最初にCSVデータが読み込まれ、次にBinarizerクラスを使用して、しきい値に応じて0と1のバイナリ値に変換されます。しきい値として0.5を使用しています。
次のスクリプトの最初の数行は、CSVデータの読み込み中に前の章で記述したものと同じです。
from pandas import read_csv
from sklearn.preprocessing import Binarizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesこれで、Binarizeクラスを使用して、データをバイナリ値に変換できます。
binarizer = Binarizer(threshold=0.5).fit(array)
Data_binarized = binarizer.transform(array)ここでは、出力の最初の5行を示しています。
print ("\nBinary data:\n", Data_binarized [0:5])出力
Binary data:
[[1. 1. 1. 1. 0. 1. 1. 1. 1.]
[1. 1. 1. 1. 0. 1. 0. 1. 0.]
[1. 1. 1. 0. 0. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 0. 1. 0.]
[0. 1. 1. 1. 1. 1. 1. 1. 1.]]標準化
基本的にガウス分布でデータ属性を変換するために使用される、もう1つの有用なデータ前処理手法。平均とSD(標準偏差)は、平均が0でSDが1の標準ガウス分布とは異なります。この手法は、線形回帰、入力データセットのガウス分布を想定してより良い結果を生成するロジスティック回帰などのMLアルゴリズムで役立ちます。再スケーリングされたデータによる結果。scikit-learn PythonライブラリのStandardScalerクラスを使用して、データ(平均= 0およびSD = 1)を標準化できます。
例
この例では、以前に使用したPima IndiansDiabetesデータセットのデータを再スケーリングします。最初にCSVデータが読み込まれ、次にStandardScalerクラスを使用して、平均= 0およびSD = 1のガウス分布に変換されます。
次のスクリプトの最初の数行は、CSVデータの読み込み中に前の章で記述したものと同じです。
from sklearn.preprocessing import StandardScaler
from pandas import read_csv
from numpy import set_printoptions
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesこれで、StandardScalerクラスを使用してデータを再スケーリングできます。
data_scaler = StandardScaler().fit(array)
data_rescaled = data_scaler.transform(array)選択に応じて、出力用のデータを要約することもできます。ここでは、精度を2に設定し、出力の最初の5行を表示しています。
set_printoptions(precision=2)
print ("\nRescaled data:\n", data_rescaled [0:5])出力
Rescaled data:
[[ 0.64 0.85 0.15 0.91 -0.69 0.2 0.47 1.43 1.37]
[-0.84 -1.12 -0.16 0.53 -0.69 -0.68 -0.37 -0.19 -0.73]
[ 1.23 1.94 -0.26 -1.29 -0.69 -1.1 0.6 -0.11 1.37]
[-0.84 -1. -0.16 0.15 0.12 -0.49 -0.92 -1.04 -0.73]
[-1.14 0.5 -1.5 0.91 0.77 1.41 5.48 -0.02 1.37]]データのラベリング
MLアルゴリズムの適切なファタの重要性と、データをMLアルゴリズムに送信する前に前処理するためのいくつかの手法について説明しました。この点に関するもう1つの側面は、データのラベル付けです。適切なラベリングを備えたMLアルゴリズムにデータを送信することも非常に重要です。たとえば、分類の問題の場合、単語や数字などの形式のラベルがデータにたくさんあります。
ラベルエンコーディングとは何ですか?
ほとんどのsklearn関数は、単語ラベルではなく番号ラベルが付いたデータを想定しています。したがって、そのようなラベルを数値ラベルに変換する必要があります。このプロセスは、ラベルエンコーディングと呼ばれます。scikit-learn PythonライブラリのLabelEncoder()関数を使用して、データのラベルエンコーディングを実行できます。
例
次の例では、Pythonスクリプトがラベルのエンコードを実行します。
まず、必要なPythonライブラリを次のようにインポートします-
import numpy as np
from sklearn import preprocessingここで、次のように入力ラベルを提供する必要があります-
input_labels = ['red','black','red','green','black','yellow','white']コードの次の行は、ラベルエンコーダーを作成し、それをトレーニングします。
encoder = preprocessing.LabelEncoder()
encoder.fit(input_labels)スクリプトの次の行は、ランダムな順序のリストをエンコードすることによってパフォーマンスをチェックします-
test_labels = ['green','red','black']
encoded_values = encoder.transform(test_labels)
print("\nLabels =", test_labels)
print("Encoded values =", list(encoded_values))
encoded_values = [3,0,4,1]
decoded_list = encoder.inverse_transform(encoded_values)次のPythonスクリプトを使用して、エンコードされた値のリストを取得できます-
print("\nEncoded values =", encoded_values)
print("\nDecoded labels =", list(decoded_list))出力
Labels = ['green', 'red', 'black']
Encoded values = [1, 2, 0]
Encoded values = [3, 0, 4, 1]
Decoded labels = ['white', 'black', 'yellow', 'green']前の章では、機械学習用のデータを前処理して準備する方法について詳しく説明しました。この章では、データ特徴選択とそれに関連するさまざまな側面について詳しく理解しましょう。
データ特徴選択の重要性
機械学習モデルのパフォーマンスは、モデルのトレーニングに使用されるデータ機能に正比例します。MLモデルに提供されるデータ機能が無関係である場合、MLモデルのパフォーマンスは悪影響を受けます。一方、関連するデータ機能を使用すると、MLモデル、特に線形回帰とロジスティック回帰の精度を高めることができます。
ここで、自動特徴選択とは何かという疑問が生じます。これは、関心のある出力変数または予測変数に最も関連するデータ内の特徴を選択するプロセスとして定義できます。属性選択とも呼ばれます。
以下は、データをモデル化する前の自動特徴選択の利点の一部です。
データモデリングの前に特徴選択を実行すると、過剰適合が減少します。
データモデリングの前に特徴選択を実行すると、MLモデルの精度が向上します。
データモデリングの前に特徴選択を実行すると、トレーニング時間が短縮されます
特徴選択手法
以下は、PythonでMLデータをモデル化するために使用できる自動特徴選択手法です。
一変量の選択
この特徴選択手法は、統計的検定の助けを借りて、予測変数と最も強い関係を持つこれらの特徴を選択するのに非常に役立ちます。scikit-learn PythonライブラリのSelectKBest0classを使用して、単変量特徴選択手法を実装できます。
Example
この例では、Pima Indians Diabetesデータセットを使用して、カイ2乗統計検定を使用して最高の機能を持つ4つの属性を選択します。
from pandas import read_csv
from numpy import set_printoptions
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.values次に、配列を入力コンポーネントと出力コンポーネントに分割します-
X = array[:,0:8]
Y = array[:,8]次のコード行は、データセットから最適な機能を選択します-
test = SelectKBest(score_func=chi2, k=4)
fit = test.fit(X,Y)選択に応じて、出力用のデータを要約することもできます。ここでは、精度を2に設定し、各属性の最高のスコアとともに、最高の機能を備えた4つのデータ属性を表示しています。
set_printoptions(precision=2)
print(fit.scores_)
featured_data = fit.transform(X)
print ("\nFeatured data:\n", featured_data[0:4])Output
[ 111.52 1411.89 17.61 53.11 2175.57 127.67 5.39 181.3 ]
Featured data:
[[148. 0. 33.6 50. ]
[ 85. 0. 26.6 31. ]
[183. 0. 23.3 32. ]
[ 89. 94. 28.1 21. ]]再帰的特徴の除去
名前が示すように、RFE(再帰的特徴除去)特徴選択手法は、属性を再帰的に削除し、残りの属性を使用してモデルを構築します。scikit-learn PythonライブラリのRFEクラスを使用して、RFE特徴選択手法を実装できます。
例
この例では、ロジスティック回帰アルゴリズムを使用したRFEを使用して、Pima IndiansDiabetesデータセットから最高の機能を持つ最高の3つの属性を選択します。
from pandas import read_csv
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.values次に、配列を入力コンポーネントと出力コンポーネントに分離します-
X = array[:,0:8]
Y = array[:,8]次のコード行は、データセットから最適な機能を選択します-
model = LogisticRegression()
rfe = RFE(model, 3)
fit = rfe.fit(X, Y)
print("Number of Features: %d")
print("Selected Features: %s")
print("Feature Ranking: %s")出力
Number of Features: 3
Selected Features: [ True False False False False True True False]
Feature Ranking: [1 2 3 5 6 1 1 4]上記の出力を見ると、RFEは最初の3つの最良の機能として、プレグ、マス、ペディを選択しています。それらは出力で1としてマークされます。
主成分分析(PCA)
一般にデータ削減手法と呼ばれるPCAは、線形代数を使用してデータセットを圧縮形式に変換するため、非常に便利な特徴選択手法です。scikit-learn PythonライブラリのPCAクラスを使用して、PCA特徴選択手法を実装できます。出力で主成分の数を選択できます。
例
この例では、PCAを使用して、Pima IndiansDiabetesデータセットから最良の3つの主成分を選択します。
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.values次に、配列を入力コンポーネントと出力コンポーネントに分割します-
X = array[:,0:8]
Y = array[:,8]次のコード行は、データセットから特徴を抽出します-
pca = PCA(n_components=3)
fit = pca.fit(X)
print("Explained Variance: %s") % fit.explained_variance_ratio_
print(fit.components_)出力
Explained Variance: [ 0.88854663 0.06159078 0.02579012]
[[ -2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-02
9.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[ 2.26488861e-02 9.72210040e-01 1.41909330e-01 -5.78614699e-02
-9.46266913e-02 4.69729766e-02 8.16804621e-04 1.40168181e-01]
[ -2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-01
2.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]]上記の出力から、3つの主成分がソースデータとほとんど類似していないことがわかります。
機能の重要性
名前が示すように、特徴重要度手法を使用して重要度特徴を選択します。基本的に、訓練された教師あり分類器を使用して特徴を選択します。この特徴選択手法は、scikit-learnPythonライブラリのExtraTreeClassifierクラスを使用して実装できます。
例
この例では、ExtraTreeClassifierを使用して、Pima IndiansDiabetesデータセットから機能を選択します。
from pandas import read_csv
from sklearn.ensemble import ExtraTreesClassifier
path = r'C:\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(data, names=names)
array = dataframe.values次に、配列を入力コンポーネントと出力コンポーネントに分割します-
X = array[:,0:8]
Y = array[:,8]次のコード行は、データセットから特徴を抽出します-
model = ExtraTreesClassifier()
model.fit(X, Y)
print(model.feature_importances_)出力
[ 0.11070069 0.2213717 0.08824115 0.08068703 0.07281761 0.14548537 0.12654214 0.15415431]出力から、各属性にスコアがあることがわかります。スコアが高いほど、その属性の重要性が高くなります。
分類入門
分類は、観測値または特定のデータポイントからクラスまたはカテゴリを予測するプロセスとして定義できます。分類された出力は、「黒」、「白」、「スパム」、「スパムなし」などの形式にすることができます。
数学的には、分類は、入力変数(X)から出力変数(Y)へのマッピング関数(f)を近似するタスクです。これは基本的に教師あり機械学習に属し、入力データセットとともにターゲットも提供されます。
分類の問題の例としては、電子メールでのスパム検出があります。出力には、「スパム」と「スパムなし」の2つのカテゴリしかありません。したがって、これはバイナリタイプの分類です。
この分類を実装するには、最初に分類器をトレーニングする必要があります。この例では、「スパム」および「スパムなし」の電子メールがトレーニングデータとして使用されます。分類器のトレーニングに成功すると、不明な電子メールを検出するために使用できます。
分類における学習者のタイプ
分類問題にはそれぞれ2種類の学習者がいます-
怠惰な学習者
名前が示すように、そのような種類の学習者は、トレーニングデータを保存した後、テストデータが表示されるのを待ちます。分類は、テストデータを取得した後にのみ行われます。彼らはトレーニングに費やす時間は少なくなりますが、予測に多くの時間を費やします。怠惰な学習者の例は、K最近傍法と事例ベースの推論です。
熱心な学習者
怠惰な学習者とは対照的に、熱心な学習者は、トレーニングデータを保存した後、テストデータが表示されるのを待たずに分類モデルを構築します。彼らはトレーニングにより多くの時間を費やしますが、予測にはより少ない時間を費やします。熱心な学習者の例は、ディシジョンツリー、ナイーブベイズ、人工ニューラルネットワーク(ANN)です。
Pythonで分類子を構築する
機械学習用のPythonライブラリであるScikit-learnを使用して、Pythonで分類子を構築できます。Pythonで分類子を作成する手順は次のとおりです-
ステップ1:必要なPythonパッケージをインポートする
scikit-learnを使用して分類器を構築するには、それをインポートする必要があります。次のスクリプトを使用してインポートできます-
import sklearnステップ2:データセットのインポート
必要なパッケージをインポートした後、分類予測モデルを構築するためのデータセットが必要です。sklearnデータセットからインポートすることも、要件に応じて他のデータセットを使用することもできます。sklearnの乳がんウィスコンシン診断データベースを使用します。次のスクリプトを使用してインポートできます-
from sklearn.datasets import load_breast_cancer次のスクリプトはデータセットをロードします。
data = load_breast_cancer()また、データを整理する必要があり、次のスクリプトを使用して行うことができます-
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']次のコマンドは、データベースの場合、ラベルの名前「悪性」および「良性」を出力します。
print(label_names)上記のコマンドの出力は、ラベルの名前です-
['malignant' 'benign']これらのラベルは、バイナリ値0および1にマップされます。 Malignant がんは0で表され、 Benign 癌は1で表されます。
これらのラベルの機能名と機能値は、次のコマンドを使用して確認できます-
print(feature_names[0])上記のコマンドの出力は、ラベル0の機能の名前です。 Malignant がん-
mean radius同様に、ラベルの特徴の名前は次のように生成できます-
print(feature_names[1])上記のコマンドの出力は、ラベル1の機能の名前です。 Benign がん-
mean texture次のコマンドを使用して、これらのラベルの機能を印刷できます-
print(features[0])これにより、次の出力が得られます-
[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
4.601e-01 1.189e-01]次のコマンドを使用して、これらのラベルの機能を印刷できます-
print(features[1])これにより、次の出力が得られます-
[2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
2.750e-01 8.902e-02]ステップ3:データをトレーニングセットとテストセットに整理する
見えないデータでモデルをテストする必要があるため、データセットをトレーニングセットとテストセットの2つの部分に分割します。sklearn pythonパッケージのtrain_test_split()関数を使用して、データをセットに分割できます。次のコマンドは関数をインポートします-
from sklearn.model_selection import train_test_split次のコマンドは、データをトレーニングデータとテストデータに分割します。この例では、データの40%をテスト目的で使用し、データの60%をトレーニング目的で使用しています。
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)ステップ4-モデル評価
データをトレーニングとテストに分割した後、モデルを構築する必要があります。この目的のために、ナイーブベイズアルゴリズムを使用します。次のコマンドはGaussianNBモジュールをインポートします-
from sklearn.naive_bayes import GaussianNBここで、モデルを次のように初期化します-
gnb = GaussianNB()次に、次のコマンドを使用して、モデルをトレーニングできます-
model = gnb.fit(train, train_labels)ここで、評価の目的で、予測を行う必要があります。これは、次のようにpredict()関数を使用して実行できます。
preds = gnb.predict(test)
print(preds)これにより、次の出力が得られます-
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0
1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0
1 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0
1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0
1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0
0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1
0 0 1 1 0 1]上記の一連の0と1の出力は、 Malignant そして Benign 腫瘍クラス。
ステップ5-精度を見つける
2つの配列、つまりtest_labelsとpredsを比較することで、前のステップでモデル構築の精度を見つけることができます。精度を決定するためにaccuracy_score()関数を使用します。
from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965上記の出力は、単純ベイズ分類器が95.17%正確であることを示しています。
分類評価指標
機械学習アプリケーションまたはモデルの実装が完了しても、ジョブは完了しません。モデルがどれほど効果的かを知る必要がありますか?さまざまな評価指標が存在する可能性がありますが、指標の選択は機械学習アルゴリズムのパフォーマンスの測定方法と比較方法に影響を与えるため、慎重に選択する必要があります。
以下は、データセットと問題の種類に基づいて選択できる重要な分類評価指標の一部です。
混同行列
これは、出力が2つ以上のタイプのクラスである可能性がある分類問題のパフォーマンスを測定する最も簡単な方法です。混同行列は、2次元のテーブルに他なりません。「実際」と「予測」、さらに、両方のディメンションには、以下に示すように、「真のポジティブ(TP)」、「真のネガティブ(TN)」、「偽のポジティブ(FP)」、「偽のネガティブ(FN)」があります。

True Positives (TP) −データポイントの実際のクラスと予測されたクラスの両方が1の場合です。
True Negatives (TN) −データポイントの実際のクラスと予測されたクラスの両方が0の場合です。
False Positives (FP) −データポイントの実際のクラスが0で、データポイントの予測クラスが1の場合です。
False Negatives (FN) −データポイントの実際のクラスが1で、データポイントの予測クラスが0の場合です。
sklearnのconfusion_matrix()関数を使用して、混同行列を見つけることができます。次のスクリプトの助けを借りて、上記で構築された二項分類器の混同行列を見つけることができます-
from sklearn.metrics import confusion_matrix出力
[[ 73 7]
[ 4 144]]正確さ
これは、MLモデルによって行われた正しい予測の数として定義できます。次の式を使用して、混同行列で簡単に計算できます。
$$=\frac{+}{+++}$$上記で構築されたバイナリ分類器の場合、TP + TN = 73 + 144 = 217およびTP + FP + FN + TN = 73 + 7 + 4 + 144 = 228。
したがって、精度= 217/228 = 0.951754385965は、バイナリ分類子を作成した後に計算したものと同じです。
精度
ドキュメントの取得に使用される精度は、MLモデルによって返される正しいドキュメントの数として定義できます。次の式を使用して、混同行列で簡単に計算できます。
$$=\frac{}{+FP}$$上で構築された二項分類器の場合、TP = 73およびTP + FP = 73 + 7 = 80です。
したがって、精度= 73/80 = 0.915
再現率または感度
リコールは、MLモデルによって返されるポジティブの数として定義できます。次の式を使用して、混同行列で簡単に計算できます。
$$=\frac{}{+FN}$$上で構築された二項分類器の場合、TP = 73およびTP + FN = 73 + 4 = 77です。
したがって、精度= 73/77 = 0.94805
特異性
リコールとは対照的に、特異性は、MLモデルによって返されるネガティブの数として定義できます。次の式を使用して、混同行列で簡単に計算できます。
$$=\frac{N}{N+FP}$$上で構築された二項分類器の場合、TN = 144およびTN + FP = 144 + 7 = 151です。
したがって、精度= 144/151 = 0.95364
さまざまなML分類アルゴリズム
以下はいくつかの重要なML分類アルゴリズムです-
ロジスティック回帰
サポートベクターマシン(SVM)
デシジョンツリー
ナイーブベイズ
ランダムフォレスト
これらすべての分類アルゴリズムについては、以降の章で詳しく説明します。
アプリケーション
分類アルゴリズムの最も重要なアプリケーションのいくつかは次のとおりです-
音声認識
手書き認識
生体認証
文書分類
ロジスティック回帰の概要
ロジスティック回帰は、ターゲット変数の確率を予測するために使用される教師あり学習分類アルゴリズムです。ターゲット変数または従属変数の性質は二分されます。つまり、可能なクラスは2つだけです。
簡単に言うと、従属変数は本質的にバイナリであり、データは1(成功/はいを表す)または0(失敗/いいえを表す)としてコード化されています。
数学的には、ロジスティック回帰モデルはXの関数としてP(Y = 1)を予測します。これは、スパム検出、糖尿病予測、癌検出などのさまざまな分類問題に使用できる最も単純なMLアルゴリズムの1つです。
ロジスティック回帰の種類
一般に、ロジスティック回帰とは、バイナリターゲット変数を持つバイナリロジスティック回帰を意味しますが、それによって予測できるターゲット変数には、さらに2つのカテゴリがあります。これらのカテゴリ数に基づいて、ロジスティック回帰は次のタイプに分類できます。
バイナリまたは二項
このような種類の分類では、従属変数は1と0の2つの可能なタイプのみを持ちます。たとえば、これらの変数は、成功または失敗、はいまたはいいえ、勝ちまたは負けなどを表す場合があります。
多項
このような種類の分類では、従属変数は3つ以上の順序付けられていないタイプ、または量的有意性のないタイプを持つことができます。たとえば、これらの変数は「タイプA」または「タイプB」または「タイプC」を表す場合があります。
序数
このような種類の分類では、従属変数は3つ以上の可能な順序付きタイプまたは量的有意性を持つタイプを持つことができます。たとえば、これらの変数は「悪い」または「良い」、「非常に良い」、「優れている」を表す場合があり、各カテゴリのスコアは0、1、2、3のようになります。
ロジスティック回帰の仮定
ロジスティック回帰の実装に飛び込む前に、同じことについて次の仮定に注意する必要があります。
バイナリロジスティック回帰の場合、ターゲット変数は常にバイナリである必要があり、目的の結果は因子レベル1で表されます。
モデルに多重共線性があってはなりません。つまり、独立変数は互いに独立している必要があります。
モデルに意味のある変数を含める必要があります。
ロジスティック回帰には、大きなサンプルサイズを選択する必要があります。
バイナリロジスティック回帰モデル
ロジスティック回帰の最も単純な形式は、ターゲット変数または従属変数が1または0の2つの可能なタイプのみを持つことができるバイナリまたは二項ロジスティック回帰です。これにより、複数の予測変数とバイナリ/二項ターゲット変数の間の関係をモデル化できます。ロジスティック回帰の場合、線形関数は基本的に次の関係のように別の関数への入力として使用されます。
$h_{\theta}{(x)}=g(\theta^{T}x)ℎ 0≤h_{\theta}≤1$ここに、次のように与えることができるロジスティック関数またはシグモイド関数があります-
$g(z)= \frac{1}{1+e^{-z}}ℎ =\theta ^{T}$シグモイド曲線は、次のグラフを使用して表すことができます。y軸の値が0と1の間にあり、0.5で軸と交差していることがわかります。

クラスはポジティブまたはネガティブに分けることができます。出力は、0から1の間にある場合、正のクラスの確率になります。この実装では、仮説関数の出力が0.5以上の場合は正として解釈され、それ以外の場合は負として解釈されます。
また、次のようにシータで表される関数の重みを使用してアルゴリズムがどの程度うまく機能するかを測定するために、損失関数を定義する必要があります。
ℎ=()
$J(\theta) = \frac{1}{m}.(-y^{T}log(h) - (1 -y)^Tlog(1-h))$ここで、損失関数を定義した後、私たちの主な目標は損失関数を最小化することです。これは、ウェイトをフィッティングすることで実行できます。つまり、ウェイトを増減することによって実行できます。各重みに対する損失関数の導関数の助けを借りて、どのパラメーターが高い重みを持つべきか、そして何がより小さな重みを持つべきかを知ることができます。
次の勾配降下方程式は、パラメータを変更した場合に損失がどのように変化するかを示しています。
$\frac{()}{\theta_{j}}=\frac{1}{m}X^{T}(()−)$Pythonでの実装
次に、Pythonで上記の二項ロジスティック回帰の概念を実装します。この目的のために、それぞれ50インスタンスの3つのクラスを持つ「iris」という名前の多変量花データセットを使用していますが、最初の2つの特徴列を使用します。すべてのクラスは、アイリスの花の一種を表しています。
まず、必要なライブラリを次のようにインポートする必要があります-
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets次に、次のようにアイリスデータセットをロードします-
iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1トレーニングデータをプロットできます。
plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();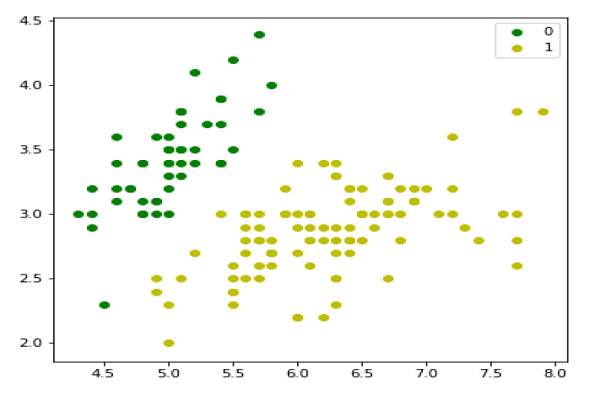
次に、シグモイド関数、損失関数、最急降下法を次のように定義します。
class LogisticRegression:
def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
self.lr = lr
self.num_iter = num_iter
self.fit_intercept = fit_intercept
self.verbose = verbose
def __add_intercept(self, X):
intercept = np.ones((X.shape[0], 1))
return np.concatenate((intercept, X), axis=1)
def __sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def __loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def fit(self, X, y):
if self.fit_intercept:
X = self.__add_intercept(X)ここで、次のように重みを初期化します。
self.theta = np.zeros(X.shape[1])
for i in range(self.num_iter):
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
gradient = np.dot(X.T, (h - y)) / y.size
self.theta -= self.lr * gradient
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
loss = self.__loss(h, y)
if(self.verbose ==True and i % 10000 == 0):
print(f'loss: {loss} \t')次のスクリプトの助けを借りて、出力確率を予測することができます-
def predict_prob(self, X):
if self.fit_intercept:
X = self.__add_intercept(X)
return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
return self.predict_prob(X).round()次に、モデルを評価し、次のようにプロットできます。
model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()
plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');
多項ロジスティック回帰モデル
ロジスティック回帰のもう1つの有用な形式は、多項ロジスティック回帰です。この回帰では、ターゲット変数または従属変数が3つ以上の順序付けられていないタイプ、つまり量的有意性のないタイプを持つことができます。
Pythonでの実装
次に、Pythonで上記の多項ロジスティック回帰の概念を実装します。この目的のために、digitという名前のsklearnのデータセットを使用しています。
まず、必要なライブラリを次のようにインポートする必要があります-
Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_split次に、数字データセットをロードする必要があります-
digits = datasets.load_digits()ここで、特徴行列(X)と応答ベクトル(y)を次のように定義します。
X = digits.data
y = digits.target次のコード行の助けを借りて、Xとyをトレーニングセットとテストセットに分割できます-
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)次に、ロジスティック回帰のオブジェクトを次のように作成します-
digreg = linear_model.LogisticRegression()ここで、次のようにトレーニングセットを使用してモデルをトレーニングする必要があります。
digreg.fit(X_train, y_train)次に、テストセットの予測を次のように行います-
y_pred = digreg.predict(X_test)次に、モデルの精度を次のように出力します-
print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)出力
Accuracy of Logistic Regression model is: 95.6884561891516上記の出力から、モデルの精度は約96%であることがわかります。
SVMの概要
サポートベクターマシン(SVM)は、分類と回帰の両方に使用される、強力でありながら柔軟な教師あり機械学習アルゴリズムです。しかし、一般的に、それらは分類問題で使用されます。1960年代に、SVMが最初に導入されましたが、その後1990年に改良されました。SVMには、他の機械学習アルゴリズムと比較して、独自の実装方法があります。最近、複数の連続変数とカテゴリ変数を処理できるため、非常に人気があります。
SVMの動作
SVMモデルは、基本的に、多次元空間の超平面内のさまざまなクラスの表現です。超平面はSVMによって反復的に生成されるため、エラーを最小限に抑えることができます。SVMの目標は、データセットをクラスに分割して、最大限界超平面(MMH)を見つけることです。

以下はSVMの重要な概念です-
Support Vectors−超平面に最も近いデータポイントはサポートベクターと呼ばれます。分離線は、これらのデータポイントを使用して定義されます。
Hyperplane −上の図からわかるように、これは、異なるクラスを持つオブジェクトのセット間で分割される決定平面または空間です。
Margin−異なるクラスのクローゼットデータポイント上の2本の線の間のギャップとして定義できます。これは、ラインからサポートベクターまでの垂直距離として計算できます。大きなマージンは良いマージンと見なされ、小さなマージンは悪いマージンと見なされます。
SVMの主な目標は、データセットをクラスに分割して最大限界超平面(MMH)を見つけることであり、次の2つの手順で実行できます。
まず、SVMは、クラスを最良の方法で分離する超平面を繰り返し生成します。
次に、クラスを正しく分離する超平面を選択します。
PythonでのSVMの実装
PythonでSVMを実装するために、次のように標準ライブラリのインポートから始めます。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns; sns.set()次に、SVM-を使用して分類するために、sklearn.dataset.sample_generatorから線形分離可能なデータを持つサンプルデータセットを作成しています。
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=0.50)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');以下は、100個のサンプルと2個のクラスターを持つサンプルデータセットを生成した後の出力です。

SVMが識別分類をサポートしていることはわかっています。2次元の場合は線を、複数次元の場合は多様体を見つけるだけで、クラスを互いに分割します。上記のデータセットに次のように実装されています-
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
plt.plot([0.6], [2.1], 'x', color='black', markeredgewidth=4, markersize=12)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);出力は次のとおりです-

上記の出力から、上記のサンプルを完全に区別する3つの異なるセパレーターがあることがわかります。
説明したように、SVMの主な目標は、データセットをクラスに分割して最大限界超平面(MMH)を見つけることです。したがって、クラス間にゼロ線を描画するのではなく、各線の周りに最も近い点までの幅のマージンを描画できます。それは次のように行うことができます-
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
上記の出力画像から、識別分類器内の「マージン」を簡単に観察できます。SVMは、マージンを最大化するラインを選択します。
次に、Scikit-Learnのサポートベクター分類器を使用して、このデータでSVMモデルをトレーニングします。ここでは、線形カーネルを使用してSVMを次のように適合させています-
from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear', C=1E10)
model.fit(X, y)出力は次のとおりです-
SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)ここで、理解を深めるために、以下に2DSVCの決定関数をプロットします。
def decision_function(model, ax=None, plot_support=True):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()モデルを評価するには、次のようにグリッドを作成する必要があります-
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)次に、決定境界とマージンを次のようにプロットする必要があります-
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])ここで、同様にサポートベクターを次のようにプロットします-
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)ここで、この関数を使用して、次のようにモデルを適合させます。
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
decision_function(model);
上記の出力から、SVM分類器がマージンを使用してデータに適合していることがわかります。つまり、破線とサポートベクター、この適合の重要な要素が破線に接触しています。これらのサポートベクターポイントは、次のように分類器のsupport_vectors_属性に格納されます。
model.support_vectors_出力は次のとおりです-
array([[0.5323772 , 3.31338909],
[2.11114739, 3.57660449],
[1.46870582, 1.86947425]])SVMカーネル
実際には、SVMアルゴリズムは、入力データ空間を必要な形式に変換するカーネルを使用して実装されます。SVMは、カーネルが低次元の入力空間を取り、それを高次元の空間に変換するカーネルトリックと呼ばれる手法を使用します。簡単に言うと、カーネルは、次元を追加することで、分離不可能な問題を分離可能な問題に変換します。これにより、SVMがより強力で、柔軟性があり、正確になります。以下は、SVMで使用されるカーネルの種類の一部です。
線形カーネル
これは、任意の2つの観測間の内積として使用できます。線形カーネルの式は次のとおりです-
k(x、x i)= sum(x * x i)
上記の式から、2つのベクトル間の積は&が入力値の各ペアの乗算の合計であると言うことがわかります。
多項式カーネル
これは線形カーネルのより一般化された形式であり、湾曲した入力空間と非線形の入力空間を区別します。以下は、多項式カーネルの式です。
K(x、xi)= 1 + sum(x * xi)^ d
ここで、dは多項式の次数であり、学習アルゴリズムで手動で指定する必要があります。
動径基底関数(RBF)カーネル
主にSVM分類で使用されるRBFカーネルは、入力空間を不定次元空間にマッピングします。次の式はそれを数学的に説明します-
K(x、xi)= exp(-gamma * sum((x – xi ^ 2))
ここで、ガンマの範囲は0〜1です。学習アルゴリズムで手動で指定する必要があります。ガンマの適切なデフォルト値は0.1です。
線形分離可能データ用にSVMを実装したので、線形分離不可能なデータ用にPythonで実装できます。カーネルを使用して実行できます。
例
以下は、カーネルを使用してSVM分類器を作成する例です。scikit-learnのアイリスデータセットを使用します-
以下のパッケージをインポートすることから始めます-
import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as pltここで、入力データをロードする必要があります-
iris = datasets.load_iris()このデータセットから、最初の2つの機能を次のように取得しています-
X = iris.data[:, :2]
y = iris.target次に、SVM境界を元のデータで次のようにプロットします-
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]ここで、正則化パラメーターの値を次のように指定する必要があります。
C = 1.0次に、SVM分類器オブジェクトを次のように作成できます。
Svc_classifier = svm.SVC(kernel = 'linear'、C = C).fit(X、y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with linear kernel')出力
Text(0.5, 1.0, 'Support Vector Classifier with linear kernel')
でSVM分類器を作成する場合 rbf カーネル、カーネルをに変更できます rbf 次のように-
Svc_classifier = svm.SVC(kernel='rbf', gamma =‘auto’,C=C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with rbf kernel')出力
Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel')
ガンマの値を「auto」に設定しますが、0から1の間の値を指定することもできます。
SVM分類器の長所と短所
SVM分類器の長所
SVM分類器は、優れた精度を提供し、高次元空間でうまく機能します。SVM分類器は基本的にトレーニングポイントのサブセットを使用するため、結果として使用するメモリは非常に少なくなります。
SVM分類器の短所
トレーニング時間が長いため、実際には大規模なデータセットには適していません。もう1つの欠点は、SVM分類器が重複するクラスではうまく機能しないことです。
デシジョンツリーの概要
一般に、デシジョンツリー分析は、多くの領域に適用できる予測モデリングツールです。決定木は、さまざまな条件に基づいてさまざまな方法でデータセットを分割できるアルゴリズムアプローチによって構築できます。決定ストレスは、教師ありアルゴリズムのカテゴリに分類される最も強力なアルゴリズムです。
これらは、分類タスクと回帰タスクの両方に使用できます。ツリーの2つの主要なエンティティは、データが分割されて結果が得られる決定ノードです。年齢、食生活、運動習慣などのさまざまな情報を提供して、人が健康か不健康かを予測するための二分木の例を以下に示します。
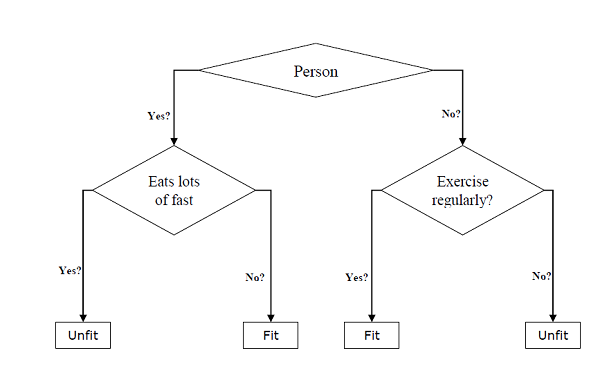
上記の決定木では、質問は決定ノードであり、最終的な結果は葉です。次の2種類の決定木があります-
Classification decision trees−この種の決定木では、決定変数はカテゴリカルです。上記の決定木は、分類決定木の例です。
Regression decision trees −この種の決定木では、決定変数は連続的です。
デシジョンツリーアルゴリズムの実装
ジニ係数
これは、データセット内のバイナリ分割を評価するために使用されるコスト関数の名前であり、カテゴリのターゲット変数「Success」または「Failure」で機能します。
ジニ係数の値が高いほど、均一性が高くなります。完全なジニ係数値は0で、最悪は0.5です(2クラスの問題の場合)。分割のジニ係数は、次の手順を使用して計算できます-
まず、成功と失敗の確率の2乗の合計である式p ^ 2 + q ^ 2を使用して、サブノードのジニ係数を計算します。
次に、その分割の各ノードの加重ジニスコアを使用して、分割のジニ係数を計算します。
分類および回帰ツリー(CART)アルゴリズムは、ジニ法を使用してバイナリ分割を生成します。
スプリットクリエーション
分割とは、基本的にデータセット内の属性と値を含むことです。次の3つの部分を使用して、データセットの分割を作成できます-
Part1 −ジニスコアの計算:前のセクションでこの部分について説明しました。
Part2−データセットの分割:データセットを、属性のインデックスとその属性の分割値を持つ2つの行リストに分割することとして定義できます。データセットから右と左の2つのグループを取得した後、最初の部分で計算されたジニスコアを使用して分割の値を計算できます。分割値は、属性がどのグループに存在するかを決定します。
Part3−すべての分割の評価:ジニスコアを見つけてデータセットを分割した後の次の部分は、すべての分割の評価です。この目的のために、最初に、候補分割として各属性に関連付けられたすべての値をチェックする必要があります。次に、分割のコストを評価して、可能な限り最良の分割を見つける必要があります。最適な分割は、決定木のノードとして使用されます。
木の構築
私たちが知っているように、ツリーにはルートノードとターミナルノードがあります。ルートノードを作成した後、次の2つの部分でツリーを構築できます-
パート1:ターミナルノードの作成
デシジョンツリーのターミナルノードを作成する際の重要なポイントの1つは、ツリーの成長を停止するタイミング、またはさらにターミナルノードを作成するタイミングを決定することです。これは、次の2つの基準、つまり最大ツリー深度と最小ノードレコードを使用して実行できます。
Maximum Tree Depth−名前が示すように、これはルートノードの後のツリー内のノードの最大数です。ツリーが最大の深さに達したら、つまりツリーが最大数のターミナルノードを取得したら、ターミナルノードの追加を停止する必要があります。
Minimum Node Records−特定のノードが担当するトレーニングパターンの最小数として定義できます。ツリーがこれらの最小ノードレコードまたはこの最小値を下回ったら、ターミナルノードの追加を停止する必要があります。
ターミナルノードは、最終的な予測を行うために使用されます。
パート2:再帰的分割
ターミナルノードを作成するタイミングについて理解したので、ツリーの構築を開始できます。再帰的分割は、ツリーを構築する方法です。この方法では、ノードが作成されると、同じ関数を何度も呼び出すことで、データセットを分割して生成されたデータの各グループに子ノード(既存のノードに追加されたノード)を再帰的に作成できます。
予測
デシジョンツリーを構築した後、それについて予測する必要があります。基本的に、予測には、特別に提供されたデータの行を使用して決定木をナビゲートすることが含まれます。
上記のように、再帰関数を使用して予測を行うことができます。同じ予測ルーチンが、左ノードまたは子右ノードで再度呼び出されます。
仮定
以下は、デシジョンツリーを作成する際に行う仮定の一部です。
デシジョンツリーを準備している間、トレーニングセットはルートノードとして機能します。
デシジョンツリー分類器は、特徴値がカテゴリカルであることを優先します。連続値を使用する場合は、モデルを構築する前に離散化する必要があります。
属性の値に基づいて、レコードは再帰的に配布されます。
統計的アプローチを使用して、ルートノードまたは内部ノードなどの任意のノード位置に属性を配置します。
Pythonでの実装
例
次の例では、ピマインディアン糖尿病に決定木分類器を実装します-
まず、必要なpythonパッケージのインポートから始めます-
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split次に、次のようにWebリンクからアイリスデータセットをダウンロードします-
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()pregnant glucose bp skin insulin bmi pedigree age label
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1ここで、データセットを次のように機能とターゲット変数に分割します-
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable次に、データをトレイン分割とテスト分割に分割します。次のコードは、データセットを70%のトレーニングデータと30%のテストデータに分割します-
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)次に、sklearnのDecisionTreeClassifierクラスを使用して、次のようにモデルをトレーニングします。
clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)最後に、予測を行う必要があります。次のスクリプトを使用して実行できます-
y_pred = clf.predict(X_test)次に、精度スコア、混同行列、分類レポートを次のように取得できます。
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)出力
Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
precision recall f1-score support
0 0.72 0.79 0.75 146
1 0.57 0.46 0.51 85
micro avg 0.67 0.67 0.67 231
macro avg 0.64 0.63 0.63 231
weighted avg 0.66 0.67 0.66 231
Accuracy: 0.670995670995671デシジョンツリーの視覚化
上記の決定木は、次のコードを使用して視覚化できます-
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())
ナイーブベイズアルゴリズムの概要
ナイーブベイズアルゴリズムは、すべての予測子が互いに独立しているという強い仮定の下でベイズの定理を適用することに基づく分類手法です。簡単に言うと、クラス内の機能の存在は、同じクラス内の他の機能の存在とは無関係であるという前提があります。たとえば、電話は、タッチスクリーン、インターネット設備、優れたカメラなどを備えている場合、スマートと見なされる場合があります。これらの機能はすべて相互に依存していますが、電話がスマートフォンである確率には独立して寄与します。
ベイズ分類では、主な関心は事後確率、つまりいくつかの観測された特徴が与えられた場合のラベルの確率を見つけることです(|)。ベイズの定理の助けを借りて、これを次のように定量的な形で表すことができます-
$P(L |features)= \frac{P(L)P(features |L)}{()}$ここで、(|)はクラスの事後確率です。
()はクラスの事前確率です。
(|)は、クラスが与えられた予測子の確率である尤度です。
()は予測子の事前確率です。
Pythonでナイーブベイズを使用してモデルを構築する
PythonライブラリであるScikitlearnは、Pythonでナイーブベイズモデルを構築するのに役立つ最も便利なライブラリです。ScikitlearnPythonライブラリの下に次の3種類のナイーブベイズモデルがあります-
ガウスナイーブベイズ
これは、各ラベルのデータが単純なガウス分布から抽出されることを前提とした、最も単純な単純ベイズ分類器です。
多項ナイーブベイズ
もう1つの有用なナイーブベイズ分類器は、特徴が単純な多項分布から抽出されると想定される多項ナイーブベイズです。このような種類のナイーブベイズは、離散カウントを表す機能に最も適しています。
ベルヌーイナイーブベイズ
もう1つの重要なモデルは、特徴がバイナリ(0と1)であると想定されるベルヌーイナイーブベイズです。「bagofwords」モデルを使用したテキスト分類は、ベルヌーイナイーブベイズのアプリケーションになります。
例
データセットに応じて、上記で説明したナイーブベイズモデルのいずれかを選択できます。ここでは、Pythonでガウスナイーブベイズモデルを実装しています-
次のように必要なインポートから始めます-
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()ここで、Scikit learnのmake_blobs()関数を使用することにより、次のようにガウス分布を持つ点のブロブを生成できます。
from sklearn.datasets import make_blobs
X, y = make_blobs(300, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');次に、GaussianNBモデルを使用するには、次のようにオブジェクトをインポートして作成する必要があります。
from sklearn.naive_bayes import GaussianNB
model_GBN = GaussianNB()
model_GNB.fit(X, y);今、私たちは予測をしなければなりません。これは、次のようにいくつかの新しいデータを生成した後に実行できます。
rng = np.random.RandomState(0)
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)
ynew = model_GNB.predict(Xnew)次に、新しいデータをプロットしてその境界を見つけます-
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
lim = plt.axis()
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='summer', alpha=0.1)
plt.axis(lim);ここで、次のコード行を使用して、1番目と2番目のラベルの事後確率を見つけることができます-
yprob = model_GNB.predict_proba(Xnew)
yprob[-10:].round(3)出力
array([[0.998, 0.002],
[1. , 0. ],
[0.987, 0.013],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[0. , 1. ],
[0.986, 0.014]])長所短所
長所
以下は、ナイーブベイズ分類器を使用することのいくつかの長所です-
ナイーブベイズ分類は、実装が簡単で高速です。
ロジスティック回帰のような識別モデルよりも速く収束します。
必要なトレーニングデータが少なくて済みます。
本質的に非常にスケーラブルであるか、予測子とデータポイントの数に比例してスケーリングします。
確率的な予測を行うことができ、連続データと離散データを処理できます。
ナイーブベイズ分類アルゴリズムは、バイナリ分類問題とマルチクラス分類問題の両方に使用できます。
短所
以下は、ナイーブベイズ分類器を使用することのいくつかの短所です-
ナイーブベイズ分類の最も重要な短所の1つは、その強力な機能の独立性です。これは、実際には、互いに完全に独立した機能のセットを持つことはほとんど不可能だからです。
ナイーブベイズ分類のもう1つの問題は、その「ゼロ頻度」です。つまり、カテゴリ変数にカテゴリがあり、トレーニングデータセットで観察されていない場合、ナイーブベイズモデルはそれにゼロの確率を割り当て、作成できなくなります。予測。
ナイーブベイズ分類の応用
以下は、ナイーブベイズ分類の一般的なアプリケーションです。
Real-time prediction −実装が容易で計算が高速なため、リアルタイムで予測を行うために使用できます。
Multi-class prediction −ナイーブベイズ分類アルゴリズムを使用して、ターゲット変数の複数のクラスの事後確率を予測できます。
Text classification−マルチクラス予測の機能により、ナイーブベイズ分類アルゴリズムはテキスト分類に非常に適しています。そのため、スパムフィルタリングや感情分析などの問題の解決にも使用されます。
Recommendation system −協調フィルタリングなどのアルゴリズムに加えて、ナイーブベイズは、目に見えない情報をフィルタリングし、ユーザーが特定のリソースを希望するかどうかを予測するために使用できるレコメンデーションシステムを作成します。
前書き
ランダムフォレストは、分類と回帰の両方に使用される教師あり学習アルゴリズムです。ただし、主に分類の問題に使用されます。私たちが知っているように、森は木で構成されており、木が多いほど、より丈夫な森を意味します。同様に、ランダムフォレストアルゴリズムは、データサンプルに決定木を作成し、それぞれから予測を取得して、最終的に投票によって最適なソリューションを選択します。これは、結果を平均化することで過剰適合を減らすため、単一の決定木よりも優れたアンサンブル手法です。
ランダムフォレストアルゴリズムの動作
次の手順を使用して、ランダムフォレストアルゴリズムの動作を理解できます。
Step1 −まず、特定のデータセットからランダムサンプルを選択することから始めます。
Step2−次に、このアルゴリズムはすべてのサンプルの決定木を構築します。次に、すべての決定木から予測結果を取得します。
Step3 −このステップでは、予測されたすべての結果に対して投票が実行されます。
Step4 −最後に、最も投票された予測結果を最終予測結果として選択します。
次の図は、その動作を示しています-

Pythonでの実装
まず、必要なPythonパッケージのインポートから始めます-
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd次に、次のようにWebリンクからアイリスデータセットをダウンロードします-
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"次に、次のようにデータセットに列名を割り当てる必要があります-
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']ここで、次のようにデータセットをパンダデータフレームに読み取る必要があります-
dataset = pd.read_csv(path, names=headernames)
dataset.head()がく片の長さ |
がく片幅 |
花びらの長さ |
花びらの幅 |
クラス |
|
|---|---|---|---|---|---|
0 |
5.1 |
3.5 |
1.4 |
0.2 |
アイリスセトサ |
1 |
4.9 |
3.0 |
1.4 |
0.2 |
アイリスセトサ |
2 |
4.7 |
3.2 |
1.3 |
0.2 |
アイリスセトサ |
3 |
4.6 |
3.1 |
1.5 |
0.2 |
アイリスセトサ |
4 |
5.0 |
3.6 |
1.4 |
0.2 |
アイリスセトサ |
データの前処理は、次のスクリプト行を使用して実行されます-
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values次に、データをトレイン分割とテスト分割に分割します。次のコードは、データセットを70%のトレーニングデータと30%のテストデータに分割します-
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)次に、sklearnのRandomForestClassifierクラスを使用して、次のようにモデルをトレーニングします。
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(n_estimators=50)
classifier.fit(X_train, y_train)最後に、予測を行う必要があります。次のスクリプトを使用して実行できます-
y_pred = classifier.predict(X_test)次に、結果を次のように出力します-
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)出力
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777ランダムフォレストの長所と短所
長所
ランダムフォレストアルゴリズムの利点は次のとおりです-
さまざまな決定木の結果を平均化または組み合わせることにより、過剰適合の問題を克服します。
ランダムフォレストは、単一の決定木よりも広範囲のデータ項目に対して適切に機能します。
ランダムフォレストは、単一の決定木よりも分散が少なくなります。
ランダムフォレストは非常に柔軟性があり、非常に高い精度を備えています。
ランダムフォレストアルゴリズムでは、データのスケーリングは必要ありません。スケーリングせずにデータを提供した後でも、良好な精度を維持します。
ランダムフォレストアルゴリズムでは、データのスケーリングは必要ありません。スケーリングせずにデータを提供した後でも、良好な精度を維持します。
短所
ランダムフォレストアルゴリズムの欠点は次のとおりです。
複雑さは、ランダムフォレストアルゴリズムの主な欠点です。
ランダムフォレストの構築は、決定木よりもはるかに困難で時間がかかります。
ランダムフォレストアルゴリズムを実装するには、より多くの計算リソースが必要です。
決定木のコレクションが多い場合は、直感的ではありません。
ランダムフォレストを使用した予測プロセスは、他のアルゴリズムと比較して非常に時間がかかります。
回帰入門
回帰は、もう1つの重要で、広く使用されている統計および機械学習ツールです。回帰ベースのタスクの主な目的は、指定された入力データについて、継続的な数値である出力ラベルまたは応答を予測することです。出力は、モデルがトレーニングフェーズで学習した内容に基づいています。基本的に、回帰モデルは、入力データの特徴(独立変数)とそれに対応する連続数値出力値(従属変数または結果変数)を使用して、入力と対応する出力の間の特定の関連付けを学習します。

回帰モデルの種類

回帰モデルには次の2つのタイプがあります-
Simple regression model −これは、予測がデータの単一の単変量特徴から形成される最も基本的な回帰モデルです。
Multiple regression model −名前が示すように、この回帰モデルでは、予測はデータの複数の特徴から形成されます。
Pythonでリグレッサを構築する
Pythonのリグレッサーモデルは、分類子を作成したのと同じように作成できます。機械学習用のPythonライブラリであるScikit-learnを使用して、Pythonでリグレッサを構築することもできます。
次の例では、データに線を当てはめる基本的な回帰モデル、つまり線形回帰モデルを構築します。Pythonでリグレッサを構築するために必要な手順は次のとおりです-
ステップ1:必要なPythonパッケージをインポートする
scikit-learnを使用してリグレッサを構築するには、他の必要なパッケージと一緒にリグレッサをインポートする必要があります。次のスクリプトを使用してをインポートできます-
import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as pltステップ2:データセットのインポート
必要なパッケージをインポートした後、回帰予測モデルを構築するためのデータセットが必要です。sklearnデータセットからインポートすることも、要件に応じて他のデータセットを使用することもできます。保存した入力データを使用します。次のスクリプトを使用してインポートできます-
input = r'C:\linear.txt'次に、このデータをロードする必要があります。np.loadtxt関数を使用してロードしています。
input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]ステップ3:データをトレーニングセットとテストセットに整理する
したがって、見えないデータでモデルをテストする必要があるため、データセットをトレーニングセットとテストセットの2つの部分に分割します。次のコマンドはそれを実行します-
training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]ステップ4-モデルの評価と予測
データをトレーニングとテストに分割した後、モデルを構築する必要があります。この目的のために、Scikit-learnのLineaRegression()関数を使用します。次のコマンドは、線形リグレッサオブジェクトを作成します。
reg_linear= linear_model.LinearRegression()次に、次のようにトレーニングサンプルを使用してこのモデルをトレーニングします。
reg_linear.fit(X_train, y_train)さて、最後に、テストデータを使用して予測を行う必要があります。
y_test_pred = reg_linear.predict(X_test)ステップ5-プロットと視覚化
予測後、次のスクリプトを使用してプロットおよび視覚化できます-
plt.scatter(X_test, y_test, color='red')
plt.plot(X_test, y_test_pred, color='black', linewidth=2)
plt.xticks(())
plt.yticks(())
plt.show()出力

上記の出力では、データポイント間の回帰直線を確認できます。
Step6- Performance computation −次のように、さまざまなパフォーマンスメトリックを使用して、回帰モデルのパフォーマンスを計算することもできます。
print("Regressor model performance:")
print("Mean absolute error(MAE) =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error(MSE) =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))出力
Regressor model performance:
Mean absolute error(MAE) = 1.78
Mean squared error(MSE) = 3.89
Median absolute error = 2.01
Explain variance score = -0.09
R2 score = -0.09ML回帰アルゴリズムの種類
最も有用で人気のあるML回帰アルゴリズムは線形回帰アルゴリズムであり、さらに2つのタイプに分けられます。
単純な線形回帰アルゴリズム
多重線形回帰アルゴリズム。
次の章では、それについて説明し、Pythonで実装します。
アプリケーション
ML回帰アルゴリズムのアプリケーションは次のとおりです-
Forecasting or Predictive analysis−回帰の重要な用途の1つは、予測または予測分析です。たとえば、GDP、石油価格、または簡単に言えば、時間の経過とともに変化する定量的データを予測できます。
Optimization−回帰の助けを借りてビジネスプロセスを最適化できます。たとえば、店長は統計モデルを作成して、顧客の来店のピーク時間を理解できます。
Error correction−ビジネスでは、正しい意思決定を行うことは、ビジネスプロセスを最適化することと同様に重要です。回帰は、すでに実装されている決定を修正する際にも、正しい決定を下すのに役立ちます。
Economics−これは経済学で最も使用されているツールです。回帰を使用して、需要、需要、消費、在庫投資などを予測できます。
Finance−金融会社は常にリスクポートフォリオを最小化することに関心があり、顧客に影響を与える要因を知りたいと考えています。これらはすべて、回帰モデルを使用して予測できます。
線形回帰の概要
線形回帰は、従属変数と特定の独立変数のセットとの間の線形関係を分析する統計モデルとして定義できます。変数間の線形関係は、1つ以上の独立変数の値が変化すると(増加または減少)、従属変数の値もそれに応じて変化する(増加または減少)ことを意味します。
数学的には、次の方程式を使用して関係を表すことができます。
Y = mX + b
ここで、Yは予測しようとしている従属変数です
Xは、予測に使用している従属変数です。
mは、XがYに与える影響を表す回帰直線の傾きです。
bは定数で、Y切片として知られています。X = 0の場合、Yはbに等しくなります。
さらに、線形関係は、以下で説明するように、本質的に正または負の場合があります。
正の線形関係
独立変数と従属変数の両方が増加した場合、線形関係は正と呼ばれます。次のグラフの助けを借りて理解することができます-

負の線形関係
独立変数が増加し、従属変数が減少する場合、線形関係は正と呼ばれます。次のグラフの助けを借りて理解することができます-

線形回帰の種類
線形回帰には次の2つのタイプがあります-
単純な線形回帰
多重線形回帰
単純線形回帰(SLR)
これは、単一の機能を使用して応答を予測する線形回帰の最も基本的なバージョンです。SLRの前提は、2つの変数が線形に関連していることです。
Pythonの実装
PythonでSLRを実装するには、2つの方法があります。1つは独自のデータセットを提供する方法、もう1つはscikit-learnpythonライブラリのデータセットを使用する方法です。
Example1 −次のPython実装例では、独自のデータセットを使用しています。
まず、必要なパッケージを次のようにインポートすることから始めます-
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt次に、SLR-の重要な値を計算する関数を定義します。
def coef_estimation(x, y):次のスクリプト行は、観測数n −を示します。
n = np.size(x)xおよびyベクトルの平均は次のように計算できます-
m_x, m_y = np.mean(x), np.mean(y)次のように、xに関する相互偏差と偏差を見つけることができます。
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_x次に、回帰係数、すなわちbは次のように計算できます。
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)次に、回帰直線をプロットし、応答ベクトルを予測する関数を定義する必要があります-
def plot_regression_line(x, y, b):次のスクリプト行は、実際のポイントを散布図としてプロットします-
plt.scatter(x, y, color = "m", marker = "o", s = 30)次のスクリプト行は、応答ベクトルを予測します-
y_pred = b[0] + b[1]*x次のスクリプト行は回帰直線をプロットし、それらにラベルを付けます-
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()最後に、データセットを提供し、上記で定義した関数を呼び出すためのmain()関数を定義する必要があります-
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()出力
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788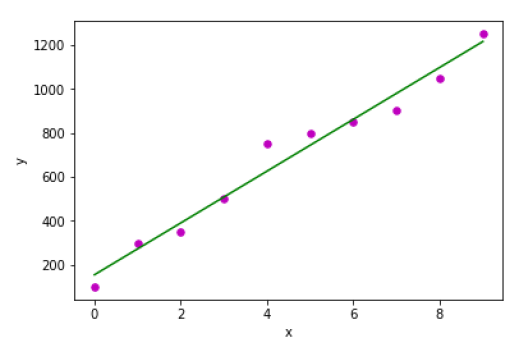
Example2 −次のPython実装例では、scikit-learnの糖尿病データセットを使用しています。
まず、必要なパッケージを次のようにインポートすることから始めます-
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score次に、糖尿病データセットをロードして、そのオブジェクトを作成します-
diabetes = datasets.load_diabetes()SLRを実装しているため、次の1つの機能のみを使用します。
X = diabetes.data[:, np.newaxis, 2]次に、次のようにデータをトレーニングセットとテストセットに分割する必要があります。
X_train = X[:-30]
X_test = X[-30:]次に、次のようにターゲットをトレーニングセットとテストセットに分割する必要があります。
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]ここで、モデルをトレーニングするには、次のように線形回帰オブジェクトを作成する必要があります。
regr = linear_model.LinearRegression()次に、次のようにトレーニングセットを使用してモデルをトレーニングします-
regr.fit(X_train, y_train)次に、次のようにテストセットを使用して予測を行います-
y_pred = regr.predict(X_test)次に、MSE、分散スコアなどの係数を次のように出力します。
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f"
% mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))ここで、出力を次のようにプロットします-
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()出力
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
重回帰(MLR)
これは、2つ以上の機能を使用して応答を予測する単純な線形回帰の拡張です。数学的には次のように説明できます-
n個の観測値、p個の特徴(独立変数)とyを1つの応答(従属変数)を持つデータセットを考えます。p個の特徴の回帰直線は次のように計算できます。
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}$ここで、H(X iが)予測された応答値とbは0、B 1、B 2 â€|、B pは回帰係数です。
複数の線形回帰モデルには、残差と呼ばれるデータ内の誤差が常に含まれているため、計算が次のように変化します。
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}+e_{i}$上記の式は次のように書くこともできます−
$y_{i}=h(x_{i})+e_{i}$ $e_{i}= y_{i} - h(x_{i})$Pythonの実装
この例では、scikitlearnのボストン住宅データセットを使用します-
まず、必要なパッケージを次のようにインポートすることから始めます-
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics次に、次のようにデータセットをロードします-
boston = datasets.load_boston(return_X_y=False)次のスクリプト行は、特徴行列Xと応答ベクトルY −を定義します。
X = boston.data
y = boston.target次に、データセットを次のようにトレーニングセットとテストセットに分割します-
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)ここで、線形回帰オブジェクトを作成し、次のようにモデルをトレーニングします。
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()出力
Coefficients:
[-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01]
Variance score: 0.709454060230326
仮定
以下は、線形回帰モデルによって作成されたデータセットに関するいくつかの仮定です。
Multi-collinearity−線形回帰モデルは、データに多重共線性がほとんどまたはまったくないことを前提としています。基本的に、多重共線性は、独立変数または特徴に依存関係がある場合に発生します。
Auto-correlation−別の仮定線形回帰モデルは、データに自己相関がほとんどまたはまったくないことを前提としています。基本的に、自己相関は、残差エラー間に依存関係がある場合に発生します。
Relationship between variables −線形回帰モデルは、応答変数と特徴変数の間の関係が線形でなければならないことを前提としています。
クラスタリング入門
クラスタリング手法は、最も有用な教師なしML手法の1つです。これらの方法は、データサンプル間の類似性と関係パターンを見つけ、それらのサンプルを特徴に基づいて類似性を持つグループにクラスター化するために使用されます。
クラスタリングは、現在のラベルのないデータ間の固有のグループ化を決定するため、重要です。それらは基本的に、それらの類似性を構成するためにデータポイントについていくつかの仮定をします。それぞれの仮定は、異なるが等しく有効なクラスターを構築します。
たとえば、以下は、異なるクラスター内の同様の種類のデータをグループ化したクラスタリングシステムを示す図です。

クラスター形成方法
クラスターが球形で形成される必要はありません。以下は、他のいくつかのクラスター形成方法です-
密度ベース
これらの方法では、クラスターは密な領域として形成されます。これらの方法の利点は、2つのクラスターをマージする優れた精度と優れた機能を備えていることです。例 ノイズのあるアプリケーションの密度ベースの空間クラスタリング(DBSCAN)、クラスタリング構造を識別するための順序付けポイント(OPTICS)など。
階層ベース
これらの方法では、クラスターは階層に基づいたツリータイプの構造として形成されます。それらには、凝集(ボトムアップアプローチ)と分割(トップダウンアプローチ)の2つのカテゴリがあります。例 代表を使用したクラスタリング(CURE)、階層を使用したバランスの取れた反復削減クラスタリング(BIRCH)など。
パーティショニング
これらの方法では、クラスターはオブジェクトをk個のクラスターに分割することによって形成されます。クラスターの数は、パーティションの数と同じになります。例 K-means、ランダム化検索(CLARANS)に基づく大規模アプリケーションのクラスタリング。
グリッド
これらの方法では、クラスターはグリッドのような構造として形成されます。これらの方法の利点は、これらのグリッドで実行されるすべてのクラスタリング操作が高速で、データオブジェクトの数に依存しないことです。例 統計情報グリッド(STING)、クエストでのクラスタリング(CLIQUE)。
クラスタリングパフォーマンスの測定
MLモデルに関する最も重要な考慮事項の1つは、そのパフォーマンスを評価することです。つまり、モデルの品質を評価することもできます。教師あり学習アルゴリズムの場合、すべての例にすでにラベルが付いているため、モデルの品質を評価するのは簡単です。
一方、教師なし学習アルゴリズムの場合、ラベルのないデータを処理するため、それほど恵まれていません。しかし、それでも、アルゴリズムに応じてクラスター内で変化が発生することについて開業医に洞察を与えるいくつかのメトリックがあります。
このようなメトリックを深く掘り下げる前に、これらのメトリックは、モデルの予測の妥当性を測定するのではなく、モデルの相互のパフォーマンスの比較のみを評価することを理解する必要があります。以下は、モデルの品質を測定するためにクラスタリングアルゴリズムにデプロイできるメトリックの一部です。
シルエット分析
クラスター間の距離を測定することにより、クラスタリングモデルの品質をチェックするために使用されるシルエット分析。基本的に、クラスターの数などのパラメーターを評価する方法を提供します。Silhouette score。このスコアは、1つのクラスター内の各ポイントが隣接するクラスター内のポイントにどれだけ近いかを測定します。
シルエットスコアの分析
シルエットスコアの範囲は[-1、1]です。その分析は次のとおりです-
+1 Score − + 1付近 Silhouette score サンプルが隣接するクラスターから遠く離れていることを示します。
0 Score − 0 Silhouette score サンプルが2つの隣接するクラスターを分離する決定境界上にあるか非常に近いことを示します。
-1 Score &minusl -1 Silhouette score サンプルが間違ったクラスターに割り当てられていることを示します。
シルエットスコアの計算は、次の式を使用して実行できます。
=(−)/(、)
ここで、=最も近いクラスター内のポイントまでの平均距離
そして、=すべてのポイントまでの平均クラスター内距離。
デイビス-ボルディンインデックス
DBインデックスは、クラスタリングアルゴリズムの分析を実行するためのもう1つの優れたメトリックです。DBインデックスの助けを借りて、クラスタリングモデルに関する次の点を理解することができます-
天気予報クラスターは互いに十分な間隔がありますか?
クラスターの密度はどれくらいですか?
次の式を使用してDBインデックスを計算できます-
$DB=\frac{1}{n}\displaystyle\sum\limits_{i=1}^n max_{j\neq{i}}\left(\frac{\sigma_{i}+\sigma_{j}}{d(c_{i},c_{j})}\right)$ここで、=クラスターの数
σ iがクラスタの重心から、クラスタ内のすべての点の平均距離を=。
DBインデックスが少ないほど、クラスタリングモデルは優れています。
ダンインデックス
DBインデックスと同じように機能しますが、両方が異なる次の点があります-
Dunnインデックスは最悪のケース、つまり互いに接近しているクラスターのみを考慮し、DBインデックスはクラスタリングモデル内のすべてのクラスターの分散と分離を考慮します。
ダンインデックスはパフォーマンスが向上するにつれて増加しますが、クラスターが十分な間隔で密集しているとDBインデックスが向上します。
次の式を使用してダン指数を計算できます-
$D=\frac{min_{1\leq i <{j}\leq{n}}P(i,j)}{mix_{1\leq i < k \leq n}q(k)}$ここで、、、 =クラスターの各インデックス
=クラスター間距離
q =クラスター内距離
MLクラスタリングアルゴリズムの種類
以下は、最も重要で有用なMLクラスタリングアルゴリズムです-
K-meansクラスタリング
このクラスタリングアルゴリズムは重心を計算し、最適な重心が見つかるまで繰り返します。クラスターの数はすでにわかっていることを前提としています。フラットクラスタリングアルゴリズムとも呼ばれます。アルゴリズムによってデータから識別されたクラスターの数は、K-meansの「K」で表されます。
平均シフトアルゴリズム
これは、教師なし学習で使用されるもう1つの強力なクラスタリングアルゴリズムです。K-meansクラスタリングとは異なり、仮定を行わないため、ノンパラメトリックアルゴリズムです。
階層的クラスタリング
これは、同様の特性を持つラベルのないデータポイントをグループ化するために使用される別の教師なし学習アルゴリズムです。
これらすべてのアルゴリズムについては、次の章で詳しく説明します。
クラスタリングのアプリケーション
クラスタリングは次の分野で役立つことがわかります-
Data summarization and compression−クラスタリングは、データの要約、圧縮、および削減が必要な領域でも広く使用されています。例としては、画像処理とベクトル量子化があります。
Collaborative systems and customer segmentation −クラスタリングは、類似の製品または同じ種類のユーザーを見つけるために使用できるため、コラボレーションシステムおよび顧客セグメンテーションの領域で使用できます。
Serve as a key intermediate step for other data mining tasks−クラスター分析は、分類、テスト、仮説生成のためのデータのコンパクトな要約を生成できます。したがって、他のデータマイニングタスクの重要な中間ステップとしても機能します。
Trend detection in dynamic data −クラスタリングは、同様の傾向のさまざまなクラスターを作成することにより、動的データの傾向検出にも使用できます。
Social network analysis−クラスタリングはソーシャルネットワーク分析で使用できます。例は、画像、ビデオ、またはオーディオでシーケンスを生成することです。
Biological data analysis −クラスタリングは、画像やビデオのクラスターを作成するためにも使用できるため、生物学的データ分析で正常に使用できます。
K-Meansアルゴリズムの概要
K-meansクラスタリングアルゴリズムは重心を計算し、最適な重心が見つかるまで繰り返します。クラスターの数はすでにわかっていることを前提としています。とも呼ばれますflat clusteringアルゴリズム。アルゴリズムによってデータから識別されたクラスターの数は、K-meansの「K」で表されます。
このアルゴリズムでは、データポイントと重心の間の距離の2乗の合計が最小になるように、データポイントがクラスターに割り当てられます。クラスター内の変動が少ないほど、同じクラスター内のより類似したデータポイントにつながることを理解されたい。
K-Meansアルゴリズムの動作
次の手順を使用して、K-Meansクラスタリングアルゴリズムの動作を理解できます。
Step1 −まず、このアルゴリズムで生成する必要のあるクラスターの数Kを指定する必要があります。
Step2−次に、K個のデータポイントをランダムに選択し、各データポイントをクラスターに割り当てます。簡単に言えば、データポイントの数に基づいてデータを分類します。
Step3 −これで、クラスターの重心が計算されます。
Step4 −次に、変化しなくなったクラスターへのデータポイントの割り当てである最適な重心が見つかるまで、以下を繰り返します。
4.1 −最初に、データポイントと重心の間の距離の2乗の合計が計算されます。
4.2 −ここで、各データポイントを他のクラスター(重心)よりも近いクラスターに割り当てる必要があります。
4.3 −最後に、そのクラスターのすべてのデータポイントの平均をとることにより、クラスターの重心を計算します。
K-meansが続きます Expectation-Maximization問題を解決するためのアプローチ。期待ステップは、データポイントを最も近いクラスターに割り当てるために使用され、最大化ステップは、各クラスターの重心を計算するために使用されます。
K-meansアルゴリズムを使用している間、次のことに注意する必要があります-
K-Meansを含むクラスタリングアルゴリズムを使用する場合、そのようなアルゴリズムは距離ベースの測定を使用してデータポイント間の類似性を判断するため、データを標準化することをお勧めします。
K-Meansの反復性と重心のランダムな初期化により、K-Meansは局所最適に固執し、全体最適に収束しない場合があります。そのため、図心のさまざまな初期化を使用することをお勧めします。
Pythonでの実装
K-Meansクラスタリングアルゴリズムを実装する次の2つの例は、理解を深めるのに役立ちます。
例1
k-meansがどのように機能するかを理解するための簡単な例です。この例では、最初に4つの異なるblobを含む2Dデータセットを生成し、その後、k-meansアルゴリズムを適用して結果を確認します。
まず、必要なパッケージをインポートすることから始めます-
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans次のコードは、4つのblobを含む2Dを生成します-
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)次に、次のコードはデータセットを視覚化するのに役立ちます-
plt.scatter(X[:, 0], X[:, 1], s=20);
plt.show()
次に、クラスターの数を提供するとともにKMeansのオブジェクトを作成し、モデルをトレーニングして、次のように予測を行います。
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)これで、次のコードを使用して、k-means Python推定量によって選択されたクラスターの中心をプロットして視覚化できます-
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9);
plt.show()
例2
単純な数字のデータセットにK-meansクラスタリングを適用する別の例に移りましょう。K-meansは、元のラベル情報を使用せずに、類似した数字を識別しようとします。
まず、必要なパッケージをインポートすることから始めます-
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans次に、sklearnから数字データセットをロードし、そのオブジェクトを作成します。このデータセットの行と列の数は、次のように見つけることもできます-
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape出力
(1797, 64)上記の出力は、このデータセットに64個の機能を持つ1797個のサンプルがあることを示しています。
上記の例1で行ったようにクラスタリングを実行できます-
kmeans = KMeans(n_clusters=10, random_state=0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape出力
(10, 64)上記の出力は、K-meansが64の機能を持つ10のクラスターを作成したことを示しています。
fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)出力
出力として、k-meansによって学習されたクラスター中心を示す次の画像が得られます。

次のコード行は、学習したクラスターラベルを、それらに含まれる実際のラベルと一致させます-
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]次に、次のように精度を確認できます。
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)出力
0.7935447968836951上記の出力は、精度が約80%であることを示しています。
長所と短所
利点
以下は、K-Meansクラスタリングアルゴリズムのいくつかの利点です。
理解と実装は非常に簡単です。
変数の数が多い場合、K-meansは階層的クラスタリングよりも高速になります。
重心の再計算時に、インスタンスはクラスターを変更できます。
階層的クラスタリングと比較して、より緊密なクラスターはK-meansで形成されます。
短所
以下は、K-Meansクラスタリングアルゴリズムのいくつかの欠点です-
クラスターの数、つまりkの値を予測するのは少し難しいです。
出力は、クラスターの数(kの値)などの初期入力の影響を強く受けます。
データの順序は、最終出力に大きな影響を与えます。
再スケーリングに非常に敏感です。正規化または標準化によってデータを再スケーリングすると、出力は完全に変更されます。最終出力。
クラスターの幾何学的形状が複雑な場合、クラスタリングジョブを実行するのは適切ではありません。
K-Meansクラスタリングアルゴリズムのアプリケーション
クラスター分析の主な目標は次のとおりです。
使用しているデータから意味のある直感を得る。
クラスター化してから、さまざまなサブグループに対してさまざまなモデルが構築される場所を予測します。
上記の目標を達成するために、K-meansクラスタリングは十分に機能しています。以下の用途に使用できます-
市場セグメンテーション
ドキュメントクラスタリング
画像セグメンテーション
画像圧縮
顧客セグメンテーション
動的データの傾向を分析する
平均シフトアルゴリズムの概要
前に説明したように、これは教師なし学習で使用されるもう1つの強力なクラスタリングアルゴリズムです。K-meansクラスタリングとは異なり、仮定はありません。したがって、これはノンパラメトリックアルゴリズムです。
平均シフトアルゴリズムは、基本的に、ポイントをデータポイントの最高密度、つまりクラスター重心に向かってシフトすることにより、データポイントをクラスターに繰り返し割り当てます。
K-MeansアルゴリズムとMean-Shiftの違いは、クラスターの数はアルゴリズムwrtデータによって決定されるため、後でクラスターの数を事前に指定する必要がないことです。
平均シフトアルゴリズムの動作
次の手順を使用して、平均シフトクラスタリングアルゴリズムの動作を理解できます。
Step1 −まず、独自のクラスターに割り当てられたデータポイントから始めます。
Step2 −次に、このアルゴリズムは重心を計算します。
Step3 −このステップでは、新しい図心の位置が更新されます。
Step4 −ここで、プロセスが繰り返され、高密度領域に移動されます。
Step5 −最後に、重心がそれ以上移動できない位置に到達すると停止します。
Pythonでの実装
Mean-Shiftアルゴリズムがどのように機能するかを理解するのは簡単な例です。この例では、最初に4つの異なるblobを含む2Dデータセットを生成し、その後、平均シフトアルゴリズムを適用して結果を確認します。
%matplotlib inline
import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.datasets.samples_generator import make_blobs
centers = [[3,3,3],[4,5,5],[3,10,10]]
X, _ = make_blobs(n_samples = 700, centers = centers, cluster_std = 0.5)
plt.scatter(X[:,0],X[:,1])
plt.show()
ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
colors = 10*['r.','g.','b.','c.','k.','y.','m.']
for i in range(len(X)):
plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 3)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
marker=".",color='k', s=20, linewidths = 5, zorder=10)
plt.show()出力
[[ 2.98462798 9.9733794 10.02629344]
[ 3.94758484 4.99122771 4.99349433]
[ 3.00788996 3.03851268 2.99183033]]
Estimated clusters: 3
長所と短所
利点
以下は、平均シフトクラスタリングアルゴリズムのいくつかの利点です。
K-meansやガウス混合のようにモデルを仮定する必要はありません。
また、非凸形状の複雑なクラスターをモデル化することもできます。
クラスターの数を自動的に決定するbandwidthという名前のパラメーターが1つだけ必要です。
K-meansのように極小値の問題はありません。
外れ値から生成された問題はありません。
短所
以下は、平均シフトクラスタリングアルゴリズムのいくつかの欠点です。
クラスターの数が急激に変化する高次元の場合、平均シフトアルゴリズムはうまく機能しません。
クラスターの数を直接制御することはできませんが、一部のアプリケーションでは、特定の数のクラスターが必要です。
意味のあるモードと意味のないモードを区別することはできません。
階層的クラスタリングの概要
階層的クラスタリングは、同様の特性を持つラベルのないデータポイントをグループ化するために使用される別の教師なし学習アルゴリズムです。階層的クラスタリングアルゴリズムは、次の2つのカテゴリに分類されます-
Agglomerative hierarchical algorithms−凝集型階層アルゴリズムでは、各データポイントは単一のクラスターとして扱われ、クラスターのペアを連続的にマージまたは凝集します(ボトムアップアプローチ)。クラスターの階層は、樹状図またはツリー構造として表されます。
Divisive hierarchical algorithms −一方、分割階層アルゴリズムでは、すべてのデータポイントが1つの大きなクラスターとして扱われ、クラスタリングのプロセスでは、1つの大きなクラスターをさまざまな小さなクラスターに分割(トップダウンアプローチ)します。
凝集型階層的クラスタリングを実行する手順
最も使用され、重要な階層的クラスタリング、つまり凝集について説明します。同じことを実行する手順は次のとおりです-
Step1−各データポイントを単一のクラスターとして扱います。したがって、最初にKクラスターを使用することになります。データポイントの数も開始時にKになります。
Step2−ここで、このステップでは、2つのクローゼットデータポイントを結合して大きなクラスターを形成する必要があります。これにより、合計でK-1クラスターになります。
Step3−ここで、さらにクラスターを形成するには、2つのクローゼットクラスターを結合する必要があります。これにより、合計K-2クラスターになります。
Step4 −ここで、1つの大きなクラスターを形成するには、Kが0になるまで、つまり結合するデータポイントがなくなるまで、上記の3つの手順を繰り返します。
Step5 −最後に、1つの大きなクラスターを作成した後、問題に応じて樹状図を使用して複数のクラスターに分割します。
凝集型階層的クラスタリングにおける樹状図の役割
最後のステップで説明したように、樹状図の役割は、大きなクラスターが形成されると始まります。樹状図は、問題に応じて、クラスターを関連するデータポイントの複数のクラスターに分割するために使用されます。次の例の助けを借りて理解することができます-
例1
理解するために、次のように必要なライブラリをインポートすることから始めましょう-
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np次に、この例で使用したデータポイントをプロットします-
X = np.array([[7,8],[12,20],[17,19],[26,15],[32,37],[87,75],[73,85], [62,80],[73,60],[87,96],])
labels = range(1, 11)
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[:,0],X[:,1], label='True Position')
for label, x, y in zip(labels, X[:, 0], X[:, 1]):
plt.annotate(label,xy=(x, y), xytext=(-3, 3),textcoords='offset points', ha='right', va='bottom')
plt.show()
上の図から、アウトデータポイントに2つのクラスターがあることは非常に簡単にわかりますが、実際のデータでは、数千のクラスターが存在する可能性があります。次に、Scipyライブラリを使用してデータポイントの樹状図をプロットします-
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
linked = linkage(X, 'single')
labelList = range(1, 11)
plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top',labels=labelList, distance_sort='descending',show_leaf_counts=True)
plt.show()
ここで、大きなクラスターが形成されると、最長の垂直距離が選択されます。次に、次の図に示すように、垂直線が引かれます。水平線が青い線と2点で交差するため、クラスターの数は2つになります。

次に、クラスタリング用のクラスをインポートし、そのfit_predictメソッドを呼び出してクラスターを予測する必要があります。sklearn.clusterライブラリのAgglomerativeClusteringクラスをインポートしています-
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(X)次に、次のコードを使用してクラスターをプロットします-
plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow')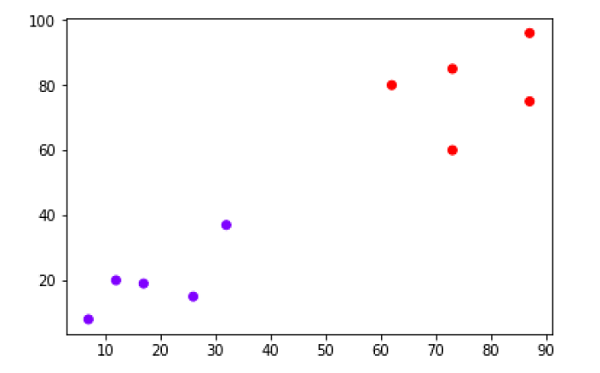
上の図は、データポイントからの2つのクラスターを示しています。
例2
上記の簡単な例から樹状図の概念を理解したので、階層的クラスタリングを使用してピマインディアン糖尿病データセットのデータポイントのクラスターを作成している別の例に移りましょう。
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
import numpy as np
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
data.shape
(768, 9)
data.head()| slno。 | プレグ | プラス | プレ | 肌 | テスト | 質量 | ペディ | 年齢 | クラス |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
patient_data = data.iloc[:, 3:5].values
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Patient Dendograms")
dend = shc.dendrogram(shc.linkage(data, method='ward'))
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
cluster.fit_predict(patient_data)
plt.figure(figsize=(10, 7))
plt.scatter(patient_data[:,0], patient_data[:,1], c=cluster.labels_, cmap='rainbow')
前書き
K最近傍(KNN)アルゴリズムは、分類と回帰予測問題の両方に使用できる教師ありMLアルゴリズムの一種です。ただし、主に業界の分類予測問題に使用されます。次の2つのプロパティは、KNNを適切に定義します-
Lazy learning algorithm − KNNは、特殊なトレーニングフェーズがなく、分類中にすべてのデータをトレーニングに使用するため、遅延学習アルゴリズムです。
Non-parametric learning algorithm − KNNは、基礎となるデータについて何も想定していないため、ノンパラメトリック学習アルゴリズムでもあります。
KNNアルゴリズムの動作
K最近傍(KNN)アルゴリズムは、「特徴の類似性」を使用して新しいデータポイントの値を予測します。これは、新しいデータポイントに、トレーニングセット内のポイントとの一致度に基づいて値が割り当てられることを意味します。次の手順でその動作を理解できます-
Step1−アルゴリズムを実装するには、データセットが必要です。したがって、KNNの最初のステップでは、トレーニングデータとテストデータをロードする必要があります。
Step2−次に、Kの値、つまり最も近いデータポイントを選択する必要があります。Kは任意の整数にすることができます。
Step3 −テストデータの各ポイントについて、以下を実行します−
3.1−ユークリッド距離、マンハッタン距離、またはハミング距離のいずれかの方法を使用して、テストデータとトレーニングデータの各行の間の距離を計算します。距離を計算するために最も一般的に使用される方法はユークリッドです。
3.2 −ここで、距離の値に基づいて、昇順で並べ替えます。
3.3 −次に、ソートされた配列から上位K行を選択します。
3.4 −ここで、これらの行の最も頻繁なクラスに基づいて、テストポイントにクラスを割り当てます。
Step4 −終了
例
以下は、Kの概念とKNNアルゴリズムの動作を理解するための例です。
次のようにプロットできるデータセットがあるとします。
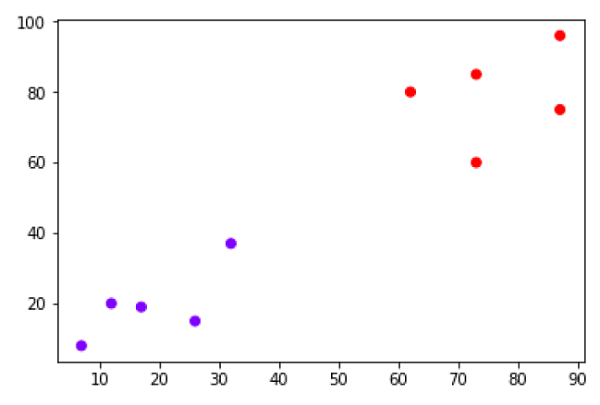
ここで、黒い点(ポイント60,60)のある新しいデータポイントを青または赤のクラスに分類する必要があります。K = 3と想定しています。つまり、最も近い3つのデータポイントが見つかります。次の図に示します-

上の図では、黒い点が付いたデータポイントの3つの最も近い隣人を見ることができます。これら3つのうち、2つは赤のクラスにあるため、黒のドットも赤のクラスに割り当てられます。
Pythonでの実装
私たちが知っているように、K最近傍(KNN)アルゴリズムは、分類と回帰の両方に使用できます。以下は、KNNを分類子および回帰子として使用するためのPythonのレシピです-
分類器としてのKNN
まず、必要なpythonパッケージのインポートから始めます-
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd次に、次のようにWebリンクからアイリスデータセットをダウンロードします-
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"次に、次のようにデータセットに列名を割り当てる必要があります-
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']ここで、次のようにデータセットをパンダデータフレームに読み取る必要があります-
dataset = pd.read_csv(path, names=headernames)
dataset.head()| slno。 | がく片の長さ | がく片幅 | 花びらの長さ | 花びらの幅 | クラス |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | アイリスセトサ |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | アイリスセトサ |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | アイリスセトサ |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | アイリスセトサ |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | アイリスセトサ |
データの前処理は、次のスクリプト行を使用して実行されます-
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values次に、データをトレイン分割とテスト分割に分割します。次のコードは、データセットを60%のトレーニングデータと40%のテストデータに分割します-
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40)次に、データのスケーリングは次のように行われます。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)次に、sklearnのKNeighborsClassifierクラスを使用して、次のようにモデルをトレーニングします。
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=8)
classifier.fit(X_train, y_train)最後に、予測を行う必要があります。次のスクリプトを使用して実行できます-
y_pred = classifier.predict(X_test)次に、結果を次のように出力します-
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)出力
Confusion Matrix:
[[21 0 0]
[ 0 16 0]
[ 0 7 16]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 21
Iris-versicolor 0.70 1.00 0.82 16
Iris-virginica 1.00 0.70 0.82 23
micro avg 0.88 0.88 0.88 60
macro avg 0.90 0.90 0.88 60
weighted avg 0.92 0.88 0.88 60
Accuracy: 0.8833333333333333リグレッサとしてのKNN
まず、必要なPythonパッケージのインポートから始めます-
import numpy as np
import pandas as pd次に、次のようにWebリンクからアイリスデータセットをダウンロードします-
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"次に、次のようにデータセットに列名を割り当てる必要があります-
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']ここで、次のようにデータセットをパンダデータフレームに読み取る必要があります-
data = pd.read_csv(url, names=headernames)
array = data.values
X = array[:,:2]
Y = array[:,2]
data.shape
output:(150, 5)次に、モデルに合うようにsklearnからKNeighborsRegressorをインポートします-
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=10)
knnr.fit(X, y)最後に、MSEは次のように見つけることができます-
print ("The MSE is:",format(np.power(y-knnr.predict(X),2).mean()))出力
The MSE is: 0.12226666666666669KNNの長所と短所
長所
理解して解釈するのは非常に単純なアルゴリズムです。
このアルゴリズムにはデータに関する仮定がないため、非線形データに非常に役立ちます。
分類と回帰に使用できるため、これは用途の広いアルゴリズムです。
精度は比較的高いですが、KNNよりもはるかに優れた教師あり学習モデルがあります。
短所
すべてのトレーニングデータを保存するため、計算量が少し高価なアルゴリズムです。
他の教師あり学習アルゴリズムと比較して、高いメモリストレージが必要です。
Nが大きい場合、予測は遅くなります。
これは、データの規模や無関係な機能に非常に敏感です。
KNNのアプリケーション
以下は、KNNをうまく適用できるいくつかの分野です-
銀行システム
KNNは銀行システムで使用して、個人がローン承認に適している天気を予測できますか?その個人は、不履行者と同様の特徴を持っていますか?
信用格付けの計算
KNNアルゴリズムを使用して、類似した特性を持つ個人と比較することにより、個人の信用格付けを見つけることができます。
政治
KNNアルゴリズムの助けを借りて、有権者候補を「投票する」、「投票しない」、「党大会に投票する」、「党に投票する」「BJP」などのさまざまなクラスに分類できます。
KNNアルゴリズムを使用できる他の領域は、音声認識、手書き検出、画像認識、およびビデオ認識です。
MLアルゴリズム、分類、回帰アルゴリズムのパフォーマンスを評価するために使用できるさまざまな指標があります。MLのパフォーマンスを評価するためのメトリックを慎重に選択する必要があります。
MLアルゴリズムのパフォーマンスを測定および比較する方法は、選択した指標に完全に依存します。
結果のさまざまな特性の重要性をどのように重み付けするかは、選択したメトリックによって完全に影響を受けます。
分類問題のパフォーマンスメトリクス
前の章で分類とそのアルゴリズムについて説明しました。ここでは、分類問題の予測を評価するために使用できるさまざまなパフォーマンスメトリックについて説明します。
混同行列
これは、出力が2つ以上のタイプのクラスである可能性がある分類問題のパフォーマンスを測定する最も簡単な方法です。混同行列は、2次元のテーブルに他なりません。「実際」と「予測」、さらに、両方のディメンションには、以下に示すように、「真のポジティブ(TP)」、「真のネガティブ(TN)」、「偽のポジティブ(FP)」、「偽のネガティブ(FN)」があります。

混同行列に関連する用語の説明は次のとおりです。
True Positives (TP) −データポイントの実際のクラスと予測されたクラスの両方が1の場合です。
True Negatives (TN) −データポイントの実際のクラスと予測されたクラスの両方が0の場合です。
False Positives (FP) −データポイントの実際のクラスが0で、データポイントの予測クラスが1の場合です。
False Negatives (FN) −データポイントの実際のクラスが1で、データポイントの予測クラスが0の場合です。
sklearn.metricsのconfusion_matrix関数を使用して、分類モデルの混同行列を計算できます。
分類精度
これは、分類アルゴリズムの最も一般的なパフォーマンスメトリックです。これは、行われたすべての予測の比率として行われた正しい予測の数として定義できます。次の式を使用して、混同行列で簡単に計算できます。
$Accuracy =\frac{TP+TN}{+++}$sklearn.metricsのaccuracy_score関数を使用して、分類モデルの精度を計算できます。
分類レポート
このレポートは、Precision、Recall、F1、およびSupportのスコアで構成されています。それらは次のように説明されます-
精度
ドキュメントの取得に使用される精度は、MLモデルによって返される正しいドキュメントの数として定義できます。次の式を使用して、混同行列で簡単に計算できます。
$Precision=\frac{TP}{TP+FP}$再現率または感度
リコールは、MLモデルによって返されるポジティブの数として定義できます。次の式を使用して、混同行列で簡単に計算できます。
$Recall =\frac{TP}{TP+FN}$特異性
リコールとは対照的に、特異性は、MLモデルによって返されるネガティブの数として定義できます。次の式を使用して、混同行列で簡単に計算できます。
$Specificity =\frac{TN}{TN+FP}$サポート
サポートは、ターゲット値の各クラスにある真の応答のサンプル数として定義できます。
F1スコア
このスコアは、適合率と再現率の調和平均を示します。数学的には、F1スコアは適合率と再現率の加重平均です。F1の最良の値は1で、最悪の値は0です。次の式を使用してF1スコアを計算できます。
= ∗(∗)/(+)
F1スコアは、適合率と再現率の相対的な寄与が等しくなっています。
sklearn.metricsのclassification_report関数を使用して、分類モデルの分類レポートを取得できます。
AUC(ROC曲線下の領域)
AUC(曲線下面積)-ROC(受信者動作特性)は、分類問題のさまざまなしきい値に基づくパフォーマンスメトリックです。名前が示すように、ROCは確率曲線であり、AUCは分離可能性を測定します。簡単に言えば、AUC-ROCメトリックは、クラスを区別する際のモデルの機能について教えてくれます。AUCが高いほど、モデルは優れています。
数学的には、TPR(True Positive Rate)、つまり感度または再現率とFPR(False Positive Rate)、つまり1-特異度をさまざまなしきい値でプロットすることで作成できます。以下は、ROC、y軸にTPR、x軸にFPRを持つAUCを示すグラフです。

sklearn.metricsのroc_auc_score関数を使用してAUC-ROCを計算できます。
LOGLOSS(対数損失)
ロジスティック回帰損失またはクロスエントロピー損失とも呼ばれます。これは基本的に確率推定に基づいて定義され、入力が0〜1の確率値である分類モデルのパフォーマンスを測定します。正確に区別することでより明確に理解できます。精度はモデル内の予測の数(予測値=実際の値)であるのに対し、ログ損失は実際のラベルとの変動量に基づく予測の不確実性の量です。Log Loss値を使用すると、モデルのパフォーマンスをより正確に表示できます。sklearn.metricsのlog_loss関数を使用して、ログ損失を計算できます。
例
以下は、Pythonでの簡単なレシピであり、バイナリ分類モデルで上記で説明したパフォーマンスメトリックをどのように使用できるかについての洞察を提供します。
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
from sklearn.metrics import log_loss
X_actual = [1, 1, 0, 1, 0, 0, 1, 0, 0, 0]
Y_predic = [1, 0, 1, 1, 1, 0, 1, 1, 0, 0]
results = confusion_matrix(X_actual, Y_predic)
print ('Confusion Matrix :')
print(results)
print ('Accuracy Score is',accuracy_score(X_actual, Y_predic))
print ('Classification Report : ')
print (classification_report(X_actual, Y_predic))
print('AUC-ROC:',roc_auc_score(X_actual, Y_predic))
print('LOGLOSS Value is',log_loss(X_actual, Y_predic))出力
Confusion Matrix :
[[3 3]
[1 3]]
Accuracy Score is 0.6
Classification Report :
precision recall f1-score support
0 0.75 0.50 0.60 6
1 0.50 0.75 0.60 4
micro avg 0.60 0.60 0.60 10
macro avg 0.62 0.62 0.60 10
weighted avg 0.65 0.60 0.60 10
AUC-ROC: 0.625
LOGLOSS Value is 13.815750437193334回帰問題のパフォーマンスメトリクス
前の章で回帰とそのアルゴリズムについて説明しました。ここでは、回帰問題の予測を評価するために使用できるさまざまなパフォーマンスメトリックについて説明します。
平均絶対誤差(MAE)
これは、回帰問題で使用される最も単純なエラーメトリックです。これは基本的に、予測値と実際の値の絶対差の平均の合計です。簡単に言えば、MAEを使用すると、予測がどれほど間違っていたかを知ることができます。MAEはモデルの方向を示しません。つまり、モデルのパフォーマンスの低下またはパフォーマンスの上昇については示しません。以下は、MAE −を計算する式です。
$MAE = \frac{1}{n}\sum|Y -\hat{Y}|$ここで、=実際の出力値
そして $\hat{Y}$=予測される出力値。
sklearn.metricsのmean_absolute_error関数を使用してMAEを計算できます。
平均二乗誤差(MSE)
MSEはMAEに似ていますが、唯一の違いは、絶対値を使用する代わりに、実際の出力値と予測された出力値の差を2乗してからすべてを合計することです。違いは次の式で確認できます-
$MSE = \frac{1}{n}\sum(Y -\hat{Y})$ここで、=実際の出力値
そして $\hat{Y}$ =予測される出力値。
sklearn.metricsのmean_squared_error関数を使用してMSEを計算できます。
決定係数(R 2)
R 2乗メトリックは通常、説明の目的で使用され、予測された出力値のセットが実際の出力値に適しているかどうかを示します。次の式は私たちがそれを理解するのに役立ちます-
$R^{2} = 1 -\frac{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\hat{Y_{i}})^2}{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\bar{Y_i)^2}}$上記の式で、分子はMSEであり、分母は値の分散です。
sklearn.metricsのr2_score関数を使用して、決定係数の2乗値を計算できます。
例
以下はPythonの簡単なレシピで、回帰モデルで上記で説明したパフォーマンスメトリックをどのように使用できるかについての洞察を提供します。
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
X_actual = [5, -1, 2, 10]
Y_predic = [3.5, -0.9, 2, 9.9]
print ('R Squared =',r2_score(X_actual, Y_predic))
print ('MAE =',mean_absolute_error(X_actual, Y_predic))
print ('MSE =',mean_squared_error(X_actual, Y_predic))出力
R Squared = 0.9656060606060606
MAE = 0.42499999999999993
MSE = 0.5674999999999999前書き
機械学習モデルを正常に実行して結果を生成するには、いくつかの標準ワークフローを自動化する必要があります。これらの標準ワークフローを自動化するプロセスは、Scikit-learnパイプラインを使用して実行できます。データサイエンティストの観点からは、パイプラインは一般化されていますが、非常に重要な概念です。基本的に、生の形式からいくつかの有用な情報へのデータフローを可能にします。パイプラインの動作は、次の図の助けを借りて理解することができます-

MLパイプラインのブロックは次のとおりです-
Data ingestion−名前が示すように、MLプロジェクトで使用するためにデータをインポートするプロセスです。データは、単一または複数のシステムからリアルタイムまたはバッチで抽出できます。データの品質がMLモデル全体に影響を与える可能性があるため、これは最も困難な手順の1つです。
Data Preparation−データをインポートした後、MLモデルで使用するデータを準備する必要があります。データ前処理は、データ準備の最も重要な手法の1つです。
ML Model Training−次のステップは、MLモデルをトレーニングすることです。データから特徴を抽出し、予測を行うために、教師あり、教師なし、強化などのさまざまなMLアルゴリズムがあります。
Model Evaluation−次に、MLモデルを評価する必要があります。AutoMLパイプラインの場合、MLモデルはさまざまな統計手法とビジネスルールを使用して評価できます。
ML Model retraining− AutoMLパイプラインの場合、最初のモデルが最適である必要はありません。最初のモデルはベースラインモデルと見なされ、モデルの精度を高めるために繰り返しトレーニングできます。
Deployment−最後に、モデルをデプロイする必要があります。このステップでは、モデルをビジネスオペレーションに適用して移行し、使用できるようにします。
MLパイプラインに伴う課題
MLパイプラインを作成するために、データサイエンティストは多くの課題に直面しています。これらの課題は、次の3つのカテゴリに分類されます-
データの品質
MLモデルの成功は、データの品質に大きく依存します。MLモデルに提供するデータが正確でなく、信頼性が高く、堅牢でない場合、間違った出力または誤解を招く出力で終了します。
データの信頼性
MLパイプラインに関連するもう1つの課題は、MLモデルに提供するデータの信頼性です。ご存知のように、データサイエンティストがデータを取得できるソースはさまざまですが、最良の結果を得るには、データソースの信頼性と信頼性を確保する必要があります。
データアクセシビリティ
MLパイプラインから最良の結果を得るには、データ自体にアクセスできる必要があり、データの統合、クレンジング、キュレーションが必要です。データアクセシビリティプロパティの結果として、メタデータは新しいタグで更新されます。
MLパイプラインのモデリングとデータ準備
トレーニングデータセットからテストデータセットに発生するデータ漏洩は、データサイエンティストがMLモデルのデータを準備する際に対処する重要な問題です。一般に、データ準備の時点で、データサイエンティストは、学習する前にデータセット全体に対して標準化や正規化などの手法を使用します。ただし、トレーニングデータセットはテストデータセット内のデータの規模に影響されるため、これらの手法ではデータの漏洩を防ぐことはできません。
MLパイプラインを使用することで、このデータ漏洩を防ぐことができます。パイプラインにより、標準化などのデータ準備が相互検証手順の各段階に制限されることが保証されるためです。
例
以下は、データの準備とモデル評価のワークフローを示すPythonの例です。この目的のために、SklearnのPima IndianDiabetesデータセットを使用しています。まず、データを標準化したパイプラインを作成します。次に、線形判別分析モデルが作成され、最後にパイプラインが10分割交差検定を使用して評価されます。
まず、必要なパッケージを次のようにインポートします-
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.discriminant_analysis import LinearDiscriminantAnalysisここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values次に、次のコードを使用してパイプラインを作成します-
estimators = []
estimators.append(('standardize', StandardScaler()))
estimators.append(('lda', LinearDiscriminantAnalysis()))
model = Pipeline(estimators)最後に、このパイプラインを評価し、その精度を次のように出力します。
kfold = KFold(n_splits=20, random_state=7)
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())出力
0.7790148448043184上記の出力は、データセットの設定の精度の要約です。
MLパイプラインと特徴抽出のモデリング
データ漏えいは、MLモデルの特徴抽出ステップでも発生する可能性があります。そのため、トレーニングデータセットのデータ漏洩を防ぐために、特徴抽出手順も制限する必要があります。データ準備の場合と同様に、MLパイプラインを使用することで、このデータ漏洩を防ぐこともできます。MLパイプラインによって提供されるツールであるFeatureUnionは、この目的に使用できます。
例
以下は、特徴抽出とモデル評価ワークフローを示すPythonの例です。この目的のために、SklearnのPima IndianDiabetesデータセットを使用しています。
まず、PCA(主成分分析)で3つの特徴を抽出します。次に、統計分析で6つの特徴を抽出します。特徴抽出後、複数の特徴選択と抽出手順の結果は、を使用して結合されます
FeatureUnionツール。最後に、ロジスティック回帰モデルが作成され、パイプラインは10分割交差検定を使用して評価されます。
まず、必要なパッケージを次のようにインポートします-
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.pipeline import FeatureUnion
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
from sklearn.feature_selection import SelectKBestここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values次に、フィーチャーユニオンは次のように作成されます-
features = []
features.append(('pca', PCA(n_components=3)))
features.append(('select_best', SelectKBest(k=6)))
feature_union = FeatureUnion(features)次に、パイプラインは次のスクリプト行の助けを借りて作成されます-
estimators = []
estimators.append(('feature_union', feature_union))
estimators.append(('logistic', LogisticRegression()))
model = Pipeline(estimators)最後に、このパイプラインを評価し、その精度を次のように出力します。
kfold = KFold(n_splits=20, random_state=7)
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())出力
0.7789811066126855上記の出力は、データセットの設定の精度の要約です。
アンサンブルによるパフォーマンスの向上
アンサンブルは、いくつかのモデルを組み合わせることで、機械学習の結果を向上させることができます。基本的に、アンサンブルモデルは、個別にトレーニングされた複数の教師あり学習モデルで構成され、それらの結果はさまざまな方法でマージされ、単一のモデルと比較してより優れた予測パフォーマンスを実現します。アンサンブル法は、次の2つのグループに分けることができます-
シーケンシャルアンサンブル法
名前が示すように、この種のアンサンブル手法では、基本学習者が順番に生成されます。このような方法の動機は、基本学習者間の依存関係を利用することです。
並列アンサンブル法
名前が示すように、これらの種類のアンサンブル手法では、基本学習者が並行して生成されます。そのような方法の動機は、基本学習者間の独立性を利用することです。
アンサンブル学習法
以下は、最も一般的なアンサンブル学習方法、つまり、異なるモデルからの予測を組み合わせる方法です。
バギング
バギングという用語は、ブートストラップ集約とも呼ばれます。バギング法では、アンサンブルモデルは、ランダムに生成されたトレーニングサンプルでトレーニングされた個々のモデルの予測を組み合わせることにより、予測精度を向上させ、モデルの分散を減少させようとします。アンサンブルモデルの最終的な予測は、個々の推定量からのすべての予測の平均を計算することによって与えられます。バギング方法の最良の例の1つは、ランダムフォレストです。
ブースティング
ブースティング法では、アンサンブルモデルを構築する主な原則は、各ベースモデル推定量を順次トレーニングすることによって段階的に構築することです。名前が示すように、基本的には、トレーニングデータの複数の反復にわたって順次トレーニングされた数週間の基本学習者を組み合わせて、強力なアンサンブルを構築します。週ベースの学習者のトレーニング中に、以前に誤分類された学習者に高い重みが割り当てられます。ブースティング方法の例はAdaBoostです。
投票
このアンサンブル学習モデルでは、さまざまなタイプの複数のモデルが構築され、平均や中央値の計算などのいくつかの単純な統計が予測を組み合わせるために使用されます。この予測は、最終的な予測を行うためのトレーニングの追加入力として機能します。
バギングアンサンブルアルゴリズム
以下は、3つのバギングアンサンブルアルゴリズムです。
袋に入れられた決定木
バギングアンサンブル法は分散の大きいアルゴリズムでうまく機能することがわかっているので、この点で最も良いのは決定木アルゴリズムです。次のPythonレシピでは、ピマ族インディアンの糖尿病データセットで、sklearnのBaggingClassifier関数とDecisionTreeClasifier(分類および回帰ツリーアルゴリズム)を使用して、袋入り決定木アンサンブルモデルを構築します。
まず、必要なパッケージを次のようにインポートします-
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifierここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]次に、次のように10分割交差検定の入力を行います-
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
cart = DecisionTreeClassifier()構築するツリーの数を指定する必要があります。ここでは150本の木を建てています-
num_trees = 150次に、次のスクリプトを使用してモデルを作成します-
model = BaggingClassifier(base_estimator=cart, n_estimators=num_trees, random_state=seed)次のように結果を計算して印刷します-
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())出力
0.7733766233766234上記の出力は、袋詰めされた決定木分類器モデルの精度が約77%であることを示しています。
ランダムフォレスト
これは、袋詰めされた決定木の拡張です。個々の分類器の場合、トレーニングデータセットのサンプルは置換されて取得されますが、ツリーはそれらの間の相関を減らすように構築されます。また、特徴のランダムなサブセットは、各ツリーの構築で最適な分割点を貪欲に選択するのではなく、各分割点を選択すると見なされます。
次のPythonレシピでは、ピマインディアンの糖尿病データセットでsklearnのRandomForestClassifierクラスを使用して、バッグ付きランダムフォレストアンサンブルモデルを構築します。
まず、必要なパッケージを次のようにインポートします-
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifierここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]次に、次のように10分割交差検定の入力を行います-
seed = 7
kfold = KFold(n_splits=10, random_state=seed)構築するツリーの数を指定する必要があります。ここでは、5つの特徴から選択された分割点を持つ150本の木を構築しています-
num_trees = 150
max_features = 5次に、次のスクリプトを使用してモデルを作成します-
model = RandomForestClassifier(n_estimators=num_trees, max_features=max_features)次のように結果を計算して印刷します-
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())出力
0.7629357484620642上記の出力は、バッグ化されたランダムフォレスト分類モデルの約76%の精度が得られたことを示しています。
余分な木
これは、バギングされた決定木アンサンブル法のもう1つの拡張です。この方法では、トレーニングデータセットのサンプルからランダムツリーが構築されます。
次のPythonレシピでは、ピマインディアンの糖尿病データセットでsklearnのExtraTreesClassifierクラスを使用して、追加のツリーアンサンブルモデルを構築します。
まず、必要なパッケージを次のようにインポートします-
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifierここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]次に、次のように10分割交差検定の入力を行います-
seed = 7
kfold = KFold(n_splits=10, random_state=seed)構築するツリーの数を指定する必要があります。ここでは、5つの特徴から選択された分割点を持つ150本の木を構築しています-
num_trees = 150
max_features = 5次に、次のスクリプトを使用してモデルを作成します-
model = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)次のように結果を計算して印刷します-
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())出力
0.7551435406698566上記の出力は、袋に入れられた追加のツリー分類モデルの約75.5%の精度が得られたことを示しています。
アンサンブルアルゴリズムのブースティング
以下は、2つの最も一般的なブースティングアンサンブルアルゴリズムです-
AdaBoost
これは、最も成功したブースティングアンサンブルアルゴリズムの1つです。このアルゴリズムの主な鍵は、データセット内のインスタンスに重みを与える方法にあります。このため、アルゴリズムは後続のモデルを構築する際にインスタンスにあまり注意を払う必要がありません。
次のPythonレシピでは、ピマインディアンの糖尿病データセットでsklearnのAdaBoostClassifierクラスを使用して、分類用のAdaBoostアンサンブルモデルを構築します。
まず、必要なパッケージを次のようにインポートします-
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifierここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]次に、次のように10分割交差検定の入力を行います-
seed = 5
kfold = KFold(n_splits=10, random_state=seed)構築するツリーの数を指定する必要があります。ここでは、5つの特徴から選択された分割点を持つ150本の木を構築しています-
num_trees = 50次に、次のスクリプトを使用してモデルを作成します-
model = AdaBoostClassifier(n_estimators=num_trees, random_state=seed)次のように結果を計算して印刷します-
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())出力
0.7539473684210527上記の出力は、AdaBoost分類器アンサンブルモデルの約75%の精度が得られたことを示しています。
確率的勾配ブースティング
勾配ブースティングマシンとも呼ばれます。次のPythonレシピでは、ピマインディアンの糖尿病データセットでsklearnのGradientBoostingClassifierクラスを使用して、分類用の確率的勾配ブースティングアンサンブルモデルを構築します。
まず、必要なパッケージを次のようにインポートします-
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifierここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Next, give the input for 10-fold cross validation as follows −
seed = 5
kfold = KFold(n_splits=10, random_state=seed)We need to provide the number of trees we are going to build. Here we are building 150 trees with split points chosen from 5 features −
num_trees = 50Next, build the model with the help of following script −
model = GradientBoostingClassifier(n_estimators=num_trees, random_state=seed)Calculate and print the result as follows −
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Output
0.7746582365003418The output above shows that we got around 77.5% accuracy of our Gradient Boosting classifier ensemble model.
Voting Ensemble Algorithms
As discussed, voting first creates two or more standalone models from training dataset and then a voting classifier will wrap the model along with taking the average of the predictions of sub-model whenever needed new data.
In the following Python recipe, we are going to build Voting ensemble model for classification by using VotingClassifier class of sklearn on Pima Indians diabetes dataset. We are combining the predictions of logistic regression, Decision Tree classifier and SVM together for a classification problem as follows −
First, import the required packages as follows −
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifierNow, we need to load the Pima diabetes dataset as did in previous examples −
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]次に、次のように10分割交差検定の入力を行います-
kfold = KFold(n_splits=10, random_state=7)次に、次のようにサブモデルを作成する必要があります-
estimators = []
model1 = LogisticRegression()
estimators.append(('logistic', model1))
model2 = DecisionTreeClassifier()
estimators.append(('cart', model2))
model3 = SVC()
estimators.append(('svm', model3))次に、上記で作成したサブモデルの予測を組み合わせて、投票アンサンブルモデルを作成します。
ensemble = VotingClassifier(estimators)
results = cross_val_score(ensemble, X, Y, cv=kfold)
print(results.mean())出力
0.7382262474367738上記の出力は、投票分類器アンサンブルモデルの精度が約74%であることを示しています。
アルゴリズムチューニングによるパフォーマンスの向上
MLモデルは、特定の問題に合わせて動作を調整できるようにパラメーター化されていることがわかっています。アルゴリズムの調整とは、MLモデルのパフォーマンスを向上させるために、これらのパラメーターの最適な組み合わせを見つけることを意味します。このプロセスはハイパーパラメータ最適化と呼ばれることもあり、アルゴリズム自体のパラメータはハイパーパラメータと呼ばれ、MLアルゴリズムによって検出された係数はパラメータと呼ばれます。
ここでは、PythonScikit-learnが提供するアルゴリズムパラメーターの調整方法について説明します。
グリッド検索パラメータの調整
これはパラメータ調整アプローチです。このメソッドの動作の重要なポイントは、グリッドで指定されたアルゴリズムパラメーターのすべての可能な組み合わせに対してモデルを系統的に構築および評価することです。したがって、このアルゴリズムは検索の性質を持っていると言えます。
例
次のPythonレシピでは、sklearnのGridSearchCVクラスを使用してグリッド検索を実行し、ピマインディアンの糖尿病データセットのリッジ回帰アルゴリズムのさまざまなアルファ値を評価します。
まず、必要なパッケージを次のようにインポートします-
import numpy
from pandas import read_csv
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCVここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]次に、さまざまなアルファ値を次のように評価します-
alphas = numpy.array([1,0.1,0.01,0.001,0.0001,0])
param_grid = dict(alpha=alphas)ここで、モデルにグリッド検索を適用する必要があります-
model = Ridge()
grid = GridSearchCV(estimator=model, param_grid=param_grid)
grid.fit(X, Y)次のスクリプト行で結果を出力します-
print(grid.best_score_)
print(grid.best_estimator_.alpha)出力
0.2796175593129722
1.0上記の出力は、最適なスコアと、そのスコアを達成したグリッド内のパラメーターのセットを示しています。この場合のアルファ値は1.0です。
ランダム検索パラメータの調整
これはパラメータ調整アプローチです。このメソッドの動作の重要なポイントは、一定の反復回数のランダム分布からアルゴリズムパラメーターをサンプリングすることです。
例
次のPythonレシピでは、sklearnのRandomizedSearchCVクラスを使用してランダム検索を実行し、ピマインディアンの糖尿病データセットのリッジ回帰アルゴリズムの0から1までのさまざまなアルファ値を評価します。
まず、必要なパッケージを次のようにインポートします-
import numpy
from pandas import read_csv
from scipy.stats import uniform
from sklearn.linear_model import Ridge
from sklearn.model_selection import RandomizedSearchCVここで、前の例で行ったように、ピマ糖尿病データセットをロードする必要があります-
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]次に、リッジ回帰アルゴリズムのさまざまなアルファ値を次のように評価します。
param_grid = {'alpha': uniform()}
model = Ridge()
random_search = RandomizedSearchCV(estimator=model, param_distributions=param_grid, n_iter=50,
random_state=7)
random_search.fit(X, Y)次のスクリプト行で結果を出力します-
print(random_search.best_score_)
print(random_search.best_estimator_.alpha)出力
0.27961712703051084
0.9779895119966027
0.9779895119966027上記の出力は、グリッド検索と同様に最適なスコアを提供します。