機械学習-スキル
機械学習の幅は非常に広く、複数のドメインにわたるスキルが必要です。機械学習のエキスパートになるために習得する必要のあるスキルは次のとおりです。
- Statistics
- 確率論
- Calculus
- 最適化手法
- Visualization
機械学習のさまざまなスキルの必要性
習得する必要のあるスキルについて簡単に説明するために、いくつかの例について説明します。
数学表記
機械学習アルゴリズムのほとんどは、数学に大きく基づいています。あなたが知る必要のある数学のレベルは、おそらく初心者レベルです。重要なのは、数学者が方程式で使用する表記法を読めるようにすることです。たとえば、表記を読んでその意味を理解できれば、機械学習を学ぶ準備ができています。そうでない場合は、数学の知識を磨く必要があるかもしれません。
$$ f_ {AN}(net- \ theta)= \ begin {cases} \ gamma&if \:net- \ theta \ geq \ epsilon \\ net- \ theta&if- \ epsilon <net- \ theta <\イプシロン\\-\ gamma&if \:net- \ theta \ leq- \ epsilon \ end {cases} $$
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i、j = 1} ^ m label ^ \ left(\ begin {array} {c} i \\ \ end {array} \ right)\ cdot \:label ^ \ left(\ begin {array} {c} j \\ \ end {array} \ right)\ cdot \:a_ {i} \ cdot \:a_ {j} \ langle x ^ \ left(\ begin {array} {c} i \\ \ end {array} \右)、x ^ \ left(\ begin {array} {c} j \\ \ end {array} \ right)\ rangle \ end {bmatrix} $$
$$ f_ {AN}(net- \ theta)= \ left(\ frac {e ^ {\ lambda(net- \ theta)}-e ^ {-\ lambda(net- \ theta)}} {e ^ { \ lambda(net- \ theta)} + e ^ {-\ lambda(net- \ theta)}} \ right)\; $$
確率論
確率論の現在の知識をテストする例を次に示します。条件付き確率による分類。
$$ p(c_ {i} | x、y)\; = \ frac {p(x、y | c_ {i})\; p(c_ {i})\;} {p(x、y)\ ;} $$
これらの定義を使用して、ベイズ分類ルールを定義できます。
- P(c1 | x、y)> P(c2 | x、y)の場合、クラスはc1です。
- P(c1 | x、y)<P(c2 | x、y)の場合、クラスはc2です。
最適化問題
これが最適化関数です
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i、j = 1} ^ m label ^ \ left(\ begin {array} {c} i \\ \ end {array} \ right)\ cdot \:label ^ \ left(\ begin {array} {c} j \\ \ end {array} \ right)\ cdot \:a_ {i} \ cdot \:a_ {j} \ langle x ^ \ left(\ begin {array} {c} i \\ \ end {array} \右)、x ^ \ left(\ begin {array} {c} j \\ \ end {array} \ right)\ rangle \ end {bmatrix} $$
以下の制約に従う-
$$ \ alpha \ geq0、and \:\ displaystyle \ sum \ limits_ {i-1} ^ m \ alpha_ {i} \ cdot \:label ^ \ left(\ begin {array} {c} i \\ \ end {配列} \ right)= 0 $$
上記を読んで理解できれば、準備は完了です。
視覚化
多くの場合、データ分布を理解し、アルゴリズムの出力の結果を解釈するには、さまざまなタイプの視覚化プロットを理解する必要があります。
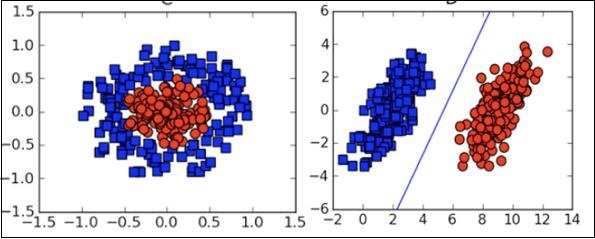
機械学習の上記の理論的側面に加えて、これらのアルゴリズムをコーディングするには、優れたプログラミングスキルが必要です。
では、MLを実装するには何が必要ですか?次の章でこれを調べてみましょう。