モデリングとシミュレーション-データベース
Modeling&Simulationのデータベースの目的は、分析とテストの目的でデータ表現とその関係を提供することです。最初のデータモデルは、1980年にエドガーコッドによって導入されました。以下は、モデルの顕著な特徴でした。
データベースは、情報とそれらの関係を定義するさまざまなデータオブジェクトのコレクションです。
ルールは、オブジェクト内のデータに対する制約を定義するためのものです。
情報を取得するための操作をオブジェクトに適用できます。
当初、データモデリングは、エンティティと関係の概念に基づいていました。エンティティはデータの情報のタイプであり、関係はエンティティ間の関連付けを表します。
データモデリングの最新の概念は、エンティティがクラスとして表されるオブジェクト指向設計であり、コンピュータプログラミングのテンプレートとして使用されます。名前、属性、制約、および他のクラスのオブジェクトとの関係を持つクラス。
その基本的な表現は次のようになります-
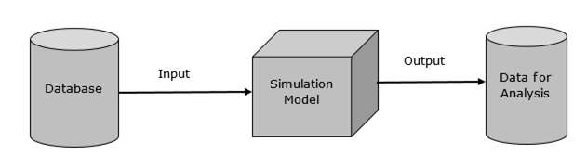
データ表現
イベントのデータ表現
シミュレーションイベントには、イベント名や関連する時間情報などの属性があります。これは、入力ファイルパラメータに関連付けられた入力データのセットを使用して提供されたシミュレーションの実行を表し、データファイルに関連付けられた複数のファイルに格納された出力データのセットとしてその結果を提供します。
入力ファイルのデータ表現
すべてのシミュレーションプロセスには、入力データファイルに表される異なる入力データとそれに関連するパラメータ値のセットが必要です。入力ファイルは、シミュレーションを処理するソフトウェアに関連付けられています。データモデルは、データファイルとの関連付けによって参照ファイルを表します。
出力ファイルのデータ表現
シミュレーションプロセスが完了すると、さまざまな出力ファイルが生成され、各出力ファイルはデータファイルとして表されます。各ファイルには、名前、説明、および普遍的な要素があります。データファイルは2つのファイルに分類されます。最初のファイルには数値が含まれ、2番目のファイルには数値ファイルの内容の説明情報が含まれています。
モデリングとシミュレーションにおけるニューラルネットワーク
ニューラルネットワークは人工知能の分野です。ニューラルネットワークは、ユニットと呼ばれる多くのプロセッサのネットワークであり、各ユニットには小さなローカルメモリがあります。各ユニットは、数値データを伝送する接続と呼ばれる単方向通信チャネルによって接続されます。各ユニットは、ローカルデータと接続から受信した入力に対してのみ機能します。
歴史
シミュレーションの歴史的な視点は、時系列で列挙されています。
最初の神経モデルはで開発されました 1940 McCulloch&Pittsによる。
に 1949、ドナルド・ヘッブは、ニューロンの概念を指摘した本「The OrganisationofBehavior」を書きました。
に 1950、コンピュータが進歩するにつれて、これらの理論のモデルを作ることが可能になりました。これはIBMの研究所によって行われました。しかし、努力は失敗し、その後の試みは成功しました。
に 1959、BernardWidrowとMarcianHoffは、ADALINEとMADALINEと呼ばれるモデルを開発しました。これらのモデルには、複数の適応型LINear要素があります。MADALINEは、現実の問題に適用された最初のニューラルネットワークでした。
に 1962、パーセプトロンモデルはRosenblattによって開発され、単純なパターン分類の問題を解決する機能を備えています。
に 1969、Minsky&Papertは、計算におけるパーセプトロンモデルの限界の数学的証明を提供しました。パーセプトロンモデルはX-OR問題を解決できないと言われていました。このような欠点は、ニューラルネットワークの一時的な衰退につながりました。
に 1982、カリフォルニア工科大学のジョン・ホップフィールドは、双方向回線を使用して機械を作成するために、彼のアイデアを全米科学アカデミーに紙で発表しました。以前は、単方向の線が使用されていました。
シンボリック手法を含む従来の人工知能技術が失敗すると、ニューラルネットワークを使用する必要が生じます。ニューラルネットワークには、そのような問題を解決するために必要な計算能力を提供する超並列技術があります。
アプリケーションエリア
ニューラルネットワークは、音声合成マシン、パターン認識、診断問題の検出、ロボット制御ボードや医療機器で使用できます。
モデリングとシミュレーションのファジィ集合
前に説明したように、連続シミュレーションの各プロセスは、微分方程式と、a、b、c、d> 0などのパラメーターに依存します。通常、点推定は計算され、モデルで使用されます。ただし、これらの推定値が不確実な場合があるため、微分方程式にファジー数が必要になります。これにより、未知のパラメーターの推定値が得られます。
ファジーセットとは何ですか?
古典的なセットでは、要素はセットのメンバーであるかどうかのいずれかです。ファジー集合は、古典的な集合の観点から定義されますX として-
A = {(x、μA(x))| x∈X}
Case 1 −関数 μA(x) 次のプロパティがあります-
∀x∈XμA(x)≥0
supx∈X{μA(x)} = 1
Case 2 −ファジィ集合しましょう B 次のように定義されます A = {(3, 0.3), (4, 0.7), (5, 1), (6, 0.4)}、その場合、その標準ファジー表記は次のように記述されます。 A = {0.3/3, 0.7/4, 1/5, 0.4/6}
メンバーシップグレードがゼロの値は、セットの式には表示されません。
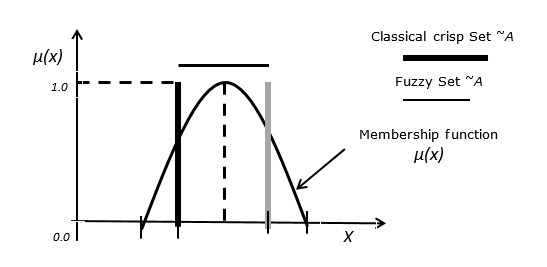
Case 3 −ファジーセットと古典的なクリスプセットの関係。
次の図は、ファジーセットと古典的なクリスプセットの関係を示しています。