並列アルゴリズム-クイックガイド

アン algorithmは、ユーザーから入力を受け取り、計算を行った後、出力を生成する一連のステップです。Aparallel algorithm は、異なる処理デバイスで複数の命令を同時に実行し、個々の出力をすべて組み合わせて最終結果を生成できるアルゴリズムです。

並行処理

インターネットの成長に伴うコンピューターの容易な入手可能性は、データの保存と処理の方法を変えました。私たちは、データが豊富にある時代に生きています。私たちは毎日、複雑なコンピューティングを必要とする膨大な量のデータを迅速に処理しています。場合によっては、同時に発生する類似または相互に関連するイベントからデータをフェッチする必要があります。これが私たちが必要とするところですconcurrent processing 複雑なタスクを分割し、複数のシステムで処理して、短時間で出力を生成できます。

タスクに大量の複雑なデータの処理が含まれる場合、並行処理は不可欠です。例としては、大規模なデータベースへのアクセス、航空機のテスト、天文学計算、原子核物理学、生物医学分析、経済計画、画像処理、ロボット工学、天気予報、Webベースのサービスなどがあります。

並列処理とは何ですか？

Parallelism複数の命令セットを同時に処理するプロセスです。合計計算時間が短縮されます。並列処理は、を使用して実装できますparallel computers,つまり、多くのプロセッサを搭載したコンピュータです。並列コンピューターには、マルチタスクをサポートする並列アルゴリズム、プログラミング言語、コンパイラー、およびオペレーティングシステムが必要です。

このチュートリアルでは、についてのみ説明します parallel algorithms。先に進む前に、まずアルゴリズムとそのタイプについて説明しましょう。

アルゴリズムとは何ですか？

アン algorithm問題を解決するために従う一連の指示です。アルゴリズムを設計する際には、アルゴリズムが実行されるコンピューターのアーキテクチャーを考慮する必要があります。アーキテクチャに従って、コンピュータには2つのタイプがあります-

シーケンシャルコンピューター
並列コンピューター

コンピュータのアーキテクチャに応じて、2種類のアルゴリズムがあります-

Sequential Algorithm −問題を解決するために、命令のいくつかの連続するステップが時系列で実行されるアルゴリズム。
Parallel Algorithm−問題はサブ問題に分割され、個別の出力を取得するために並行して実行されます。後で、これらの個々の出力を組み合わせて、最終的な目的の出力を取得します。

大きな問題をに分割するのは簡単ではありません sub-problems。サブ問題には、データの依存関係がある場合があります。したがって、プロセッサは問題を解決するために相互に通信する必要があります。

プロセッサが相互に通信するのに必要な時間は、実際の処理時間よりも長いことがわかっています。したがって、並列アルゴリズムを設計する際には、効率的なアルゴリズムを取得するために適切なCPU使用率を考慮する必要があります。

アルゴリズムを適切に設計するには、基本的な考え方を明確にする必要があります。 model of computation 並列コンピューターで。

計算モデル

シーケンシャルコンピューターと並列コンピューターはどちらも、アルゴリズムと呼ばれる一連の命令（ストリーム）で動作します。これらの一連の命令（アルゴリズム）は、各ステップで何をしなければならないかについてコンピューターに指示します。

命令ストリームとデータストリームに応じて、コンピュータは4つのカテゴリに分類できます-

単一命令ストリーム、単一データストリーム（SISD）コンピューター
単一命令ストリーム、複数データストリーム（SIMD）コンピューター
マルチインストラクションストリーム、シングルデータストリーム（MISD）コンピューター
複数の命令ストリーム、複数のデータストリーム（MIMD）コンピューター

SISDコンピューター

SISDコンピュータには one control unit, one processing unit, そして one memory unit。

このタイプのコンピュータでは、プロセッサは制御ユニットから命令の単一ストリームを受信し、メモリユニットからのデータの単一ストリームで動作します。計算中、各ステップで、プロセッサは制御ユニットから1つの命令を受け取り、メモリユニットから受け取った単一のデータを操作します。

SIMDコンピューター

SIMDコンピューターには one control unit, multiple processing units, そして shared memory or interconnection network。

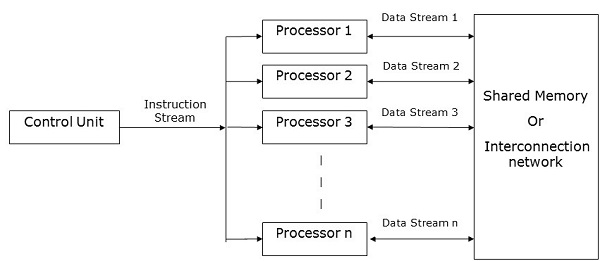
ここでは、1つの制御ユニットがすべての処理ユニットに命令を送信します。計算中、各ステップで、すべてのプロセッサは制御ユニットから単一の命令セットを受け取り、メモリユニットからの異なるデータセットを操作します。

各処理ユニットには、データと命令の両方を格納するための独自のローカルメモリユニットがあります。SIMDコンピューターでは、プロセッサーはプロセッサー間で通信する必要があります。これはによって行われますshared memory またはによって interconnection network。

一部のプロセッサは一連の命令を実行しますが、残りのプロセッサは次の一連の命令を待ちます。コントロールユニットからの指示により、どのプロセッサを使用するかが決まりますactive （実行手順）または inactive （次の指示を待ちます）。

MISDコンピューター

名前が示すように、MISDコンピュータには multiple control units, multiple processing units, そして one common memory unit。

ここでは、各プロセッサに独自の制御ユニットがあり、共通のメモリユニットを共有しています。すべてのプロセッサは、それぞれの制御ユニットから個別に命令を受け取り、それぞれの制御ユニットから受け取った命令に従って、単一のデータストリームを操作します。このプロセッサは同時に動作します。

MIMDコンピューター

MIMDコンピュータには multiple control units, multiple processing units, と shared memory または interconnection network。

ここで、各プロセッサには、独自の制御ユニット、ローカルメモリユニット、および算術論理演算ユニットがあります。それらは、それぞれの制御ユニットから異なるセットの命令を受け取り、異なるセットのデータを操作します。

注意

共通のメモリを共有するMIMDコンピュータは、 multiprocessors, 一方、相互接続ネットワークを使用するものは、 multicomputers。
プロセッサの物理的な距離に基づいて、マルチコンピュータには2つのタイプがあります-
- Multicomputer −すべてのプロセッサが互いに非常に接近している場合（たとえば、同じ部屋にある場合）。
- Distributed system −すべてのプロセッサが互いに遠く離れている場合（たとえば、異なる都市）

アルゴリズムの分析は、アルゴリズムが有用かどうかを判断するのに役立ちます。一般に、アルゴリズムはその実行時間に基づいて分析されます(Time Complexity) とスペースの量 (Space Complexity) 必要です。

洗練されたメモリデバイスをリーズナブルなコストで利用できるため、ストレージスペースはもはや問題ではありません。したがって、スペースの複雑さはそれほど重要ではありません。

並列アルゴリズムは、コンピューターの計算速度を向上させるように設計されています。並列アルゴリズムを分析するために、通常、次のパラメーターを考慮します。

時間計算量（実行時間）、
使用されたプロセッサの総数、および
総費用。

時間計算量

並列アルゴリズムの開発の背後にある主な理由は、アルゴリズムの計算時間を短縮することでした。したがって、アルゴリズムの実行時間を評価することは、その効率を分析する上で非常に重要です。

実行時間は、アルゴリズムが問題を解決するのにかかる時間に基づいて測定されます。合計実行時間は、アルゴリズムが実行を開始した瞬間から停止する瞬間まで計算されます。すべてのプロセッサが同時に実行を開始または終了しない場合、アルゴリズムの合計実行時間は、最初のプロセッサが実行を開始した瞬間から最後のプロセッサが実行を停止した瞬間までです。

アルゴリズムの時間計算量は、3つのカテゴリに分類できます-

Worst-case complexity −特定の入力に対してアルゴリズムに必要な時間が次の場合 maximum。
Average-case complexity −特定の入力に対してアルゴリズムに必要な時間が次の場合 average。
Best-case complexity −特定の入力に対してアルゴリズムに必要な時間が次の場合 minimum。

漸近解析

アルゴリズムの複雑さまたは効率は、目的の出力を取得するためにアルゴリズムによって実行されるステップの数です。漸近分析は、理論的分析におけるアルゴリズムの複雑さを計算するために行われます。漸近解析では、アルゴリズムの複雑さ関数を計算するために、長い入力が使用されます。

Note − Asymptotic線が曲線と交わる傾向があるが、それらが交差しない状態です。ここでは、線と曲線は互いに漸近的です。

漸近表記は、速度の上限と下限を使用するアルゴリズムの可能な限り速い実行時間と最も遅い実行時間を記述する最も簡単な方法です。このために、次の表記法を使用します-

ビッグO表記
オメガ表記
シータ表記

ビッグO表記

数学では、関数の漸近特性を表すためにBigO表記が使用されます。これは、単純で正確な方法で、大きな入力に対する関数の動作を表します。これは、アルゴリズムの実行時間の上限を表す方法です。これは、アルゴリズムが実行を完了するのにかかる可能性のある最長の時間を表します。関数-

f（n）= O（g（n））

正の定数が存在する場合 c そして n₀ そのような f(n) ≤ c * g(n) すべてのために n どこ n ≥ n₀。

オメガ表記

オメガ表記は、アルゴリズムの実行時間の下限を表す方法です。関数-

f（n）=Ω（g（n））

正の定数が存在する場合 c そして n₀ そのような f(n) ≥ c * g(n) すべてのために n どこ n ≥ n₀。

シータ表記

シータ表記は、アルゴリズムの実行時間の下限と上限の両方を表す方法です。関数-

f（n）=θ（g（n））

正の定数が存在する場合 c₁, c₂, そして n₀ すべてについてc1 * g（n）≤f（n）≤c2* g（n）となるように n どこ n ≥ n₀。

アルゴリズムの高速化

並列アルゴリズムのパフォーマンスは、その計算によって決定されます speedup。スピードアップは、並列アルゴリズムの最悪の実行時間に対する、特定の問題に対する最速の既知の順次アルゴリズムの最悪の実行時間の比率として定義されます。

スピードアップ=

特定の問題に対する最速の既知のシーケンシャルの最悪実行時間/ 並列アルゴリズムの最悪実行時間

使用されたプロセッサーの数

使用されるプロセッサの数は、並列アルゴリズムの効率を分析する上で重要な要素です。コンピューターの購入、保守、および実行にかかるコストが計算されます。問題を解決するためにアルゴリズムが使用するプロセッサの数が多いほど、得られる結果のコストが高くなります。

総費用

並列アルゴリズムの総コストは、時間の複雑さとその特定のアルゴリズムで使用されるプロセッサの数の積です。

総コスト=時間計算量×使用されたプロセッサの数

したがって、 efficiency 並列アルゴリズムのは-

効率=

シーケンシャルアルゴリズムの最悪実行時間/ 並列アルゴリズムの最悪実行時間

並列アルゴリズムのモデルは、データと処理方法を分割するための戦略を検討し、相互作用を減らすために適切な戦略を適用することによって開発されます。この章では、次の並列アルゴリズムモデルについて説明します。

データ並列モデル
タスクグラフモデル
作業プールモデル
マスタースレーブモデル
プロデューサーコンシューマーまたはパイプラインモデル
ハイブリッドモデル

データ並列

データ並列モデルでは、タスクがプロセスに割り当てられ、各タスクが異なるデータに対して同様のタイプの操作を実行します。 Data parallelism これは、複数のデータ項目に適用されている単一の操作の結果です。

データ並列モデルは、共有アドレス空間とメッセージパッシングパラダイムに適用できます。データ並列モデルでは、局所性を維持する分解を選択するか、最適化された集合的な相互作用ルーチンを使用するか、計算と相互作用を重複させることにより、相互作用のオーバーヘッドを減らすことができます。

データ並列モデルの問題の主な特徴は、データの並列性の強度が問題のサイズとともに増加することです。これにより、より多くのプロセスを使用してより大きな問題を解決できるようになります。

Example −密な行列の乗算。

タスクグラフモデル

タスクグラフモデルでは、並列処理は次のように表されます。 task graph。タスクグラフは、取るに足らないものでも、取るに足らないものでもかまいません。このモデルでは、タスク間の相関関係を利用して、局所性を促進したり、対話コストを最小限に抑えたりします。このモデルは、タスクに関連付けられた計算の数と比較して、タスクに関連付けられたデータの量が膨大であるという問題を解決するために適用されます。タスクは、タスク間のデータ移動のコストを改善するために割り当てられます。

Examples −分割統治法によって導出された並列クイックソート、スパース行列因数分解、および並列アルゴリズム。

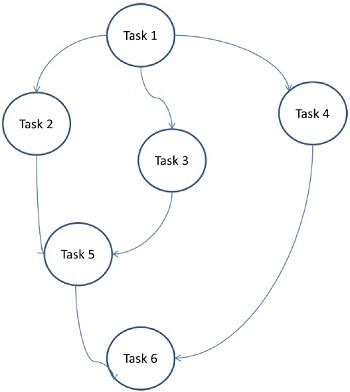
ここでは、問題がアトミックタスクに分割され、グラフとして実装されます。各タスクは、1つ以上の先行タスクに依存する独立したジョブ単位です。タスクの完了後、先行タスクの出力が依存タスクに渡されます。先行タスクのあるタスクは、先行タスク全体が完了したときにのみ実行を開始します。グラフの最終出力は、最後の依存タスクが完了したときに受信されます（上の図のタスク6）。

作業プールモデル

ワークプールモデルでは、負荷を分散するためにタスクがプロセスに動的に割り当てられます。したがって、任意のプロセスが任意のタスクを実行する可能性があります。このモデルは、タスクに関連付けられたデータの量がタスクに関連付けられた計算よりも比較的少ない場合に使用されます。

プロセスへのタスクの望ましい事前割り当てはありません。タスクの割り当ては集中化または分散化されています。タスクへのポインタは、物理的に共有されたリスト、優先度キュー、またはハッシュテーブルやツリーに保存されます。あるいは、物理的に分散されたデータ構造に保存されることもあります。

タスクは最初から利用できる場合もあれば、動的に生成される場合もあります。タスクが動的に生成され、タスクの分散割り当てが行われる場合、すべてのプロセスが実際にプログラム全体の完了を検出し、それ以上のタスクの検索を停止できるように、終了検出アルゴリズムが必要です。

Example −並列ツリー検索

マスタースレーブモデル

マスタースレーブモデルでは、1つ以上のマスタープロセスがタスクを生成し、それをスレーブプロセスに割り当てます。次の場合、タスクは事前に割り当てられます。

マスターはタスクの量を見積もることができます、または
ランダムな割り当ては、負荷のバランスをとるという満足のいく仕事をすることができます。
スレーブには、異なる時間に小さなタスクが割り当てられます。

このモデルは、一般的に shared-address-space または message-passing paradigms, 相互作用は当然2つの方法であるためです。

場合によっては、タスクを段階的に完了する必要があり、次の段階のタスクを生成する前に、各段階のタスクを完了する必要があります。マスタースレーブモデルは、次のように一般化できます。hierarchical または multi-level master-slave model トップレベルのマスターがタスクの大部分をセカンドレベルのマスターにフィードします。セカンドレベルのマスターは、タスクを自身のスレーブ間でさらに細分化し、タスク自体の一部を実行できます。

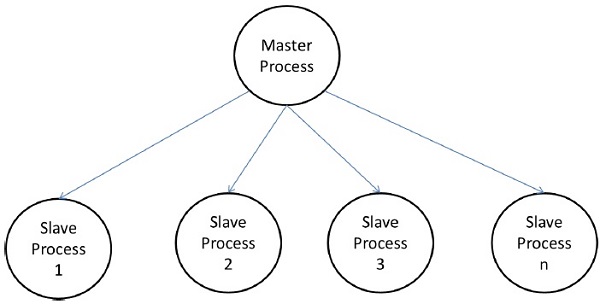
マスタースレーブモデルを使用する際の注意事項

マスターが混雑ポイントにならないように注意する必要があります。タスクが小さすぎるか、作業者が比較的速い場合に発生する可能性があります。

タスクは、タスクを実行するコストが通信のコストと同期のコストを支配するように選択する必要があります。

非同期の相互作用は、マスターによる作業生成に関連する相互作用と計算の重複に役立つ場合があります。

パイプラインモデル

としても知られています producer-consumer model。ここでは、一連のデータが一連のプロセスを介して渡され、各プロセスが何らかのタスクを実行します。ここで、新しいデータの到着は、キュー内のプロセスによる新しいタスクの実行を生成します。プロセスは、線形または多次元の配列、ツリー、またはサイクルの有無にかかわらず一般的なグラフの形でキューを形成できます。

このモデルは、生産者と消費者のチェーンです。キュー内の各プロセスは、キュー内で先行するプロセスの一連のデータアイテムのコンシューマー、およびキュー内で後続するプロセスのデータのプロデューサーと見なすことができます。キューは線形チェーンである必要はありません。有向グラフにすることができます。このモデルに適用できる最も一般的な相互作用最小化手法は、相互作用と計算の重複です。

Example −並列LU分解アルゴリズム。

ハイブリッドモデル

問題を解決するために複数のモデルが必要になる可能性がある場合は、ハイブリッドアルゴリズムモデルが必要です。

ハイブリッドモデルは、階層的に適用される複数のモデル、または並列アルゴリズムの異なるフェーズに順次適用される複数のモデルのいずれかで構成されます。

Example −並列クイックソート

Parallel Random Access Machines (PRAM)はモデルであり、ほとんどの並列アルゴリズムで考慮されています。ここでは、複数のプロセッサが1つのメモリブロックに接続されています。PRAMモデルには次のものが含まれます-

同様のタイプのプロセッサのセット。
すべてのプロセッサは共通のメモリユニットを共有します。プロセッサは、共有メモリを介してのみ相互に通信できます。
メモリアクセスユニット（MAU）は、プロセッサを単一の共有メモリに接続します。

ここに、 n 多数のプロセッサが独立した操作を実行できます n特定の時間単位でのデータの数。これにより、異なるプロセッサが同じメモリ位置に同時にアクセスする可能性があります。

この問題を解決するために、次の制約がPRAMモデルに適用されています。

Exclusive Read Exclusive Write (EREW) −ここでは、2つのプロセッサが同じメモリ位置から同時に読み取りまたは書き込みを行うことはできません。
Exclusive Read Concurrent Write (ERCW) −ここでは、2つのプロセッサが同じメモリ位置から同時に読み取ることはできませんが、同じメモリ位置に同時に書き込むことはできます。
Concurrent Read Exclusive Write (CREW) −ここでは、すべてのプロセッサが同じメモリ位置から同時に読み取ることは許可されていますが、同じメモリ位置に同時に書き込むことは許可されていません。
Concurrent Read Concurrent Write (CRCW) −すべてのプロセッサは、同じメモリ位置から同時に読み取りまたは書き込みを行うことができます。

PRAMモデルを実装する方法はたくさんありますが、最も顕著な方法は次のとおりです。

共有メモリモデル
メッセージパッシングモデル
データ並列モデル

共有メモリモデル

共有メモリは control parallelism 上より data parallelism。共有メモリモデルでは、複数のプロセスが異なるプロセッサで独立して実行されますが、それらは共通のメモリ空間を共有します。プロセッサのアクティビティが原因で、メモリの場所に変更があった場合、それは残りのプロセッサに表示されます。

複数のプロセッサが同じメモリ位置にアクセスすると、特定の時点で、複数のプロセッサが同じメモリ位置にアクセスする場合があります。一方がその場所を読み取り、もう一方がその場所に書き込んでいるとします。混乱を招く可能性があります。これを回避するために、次のようないくつかの制御メカニズムlock / semaphore, 相互排除を確実にするために実装されます。

共有メモリプログラミングは、以下で実装されています。

Thread libraries−スレッドライブラリは、同じメモリ位置で同時に実行される複数の制御スレッドを許可します。スレッドライブラリは、サブルーチンのライブラリを介したマルチスレッドをサポートするインターフェイスを提供します。のサブルーチンが含まれています
- スレッドの作成と破棄
- スレッドの実行のスケジューリング
- スレッド間でデータとメッセージを渡す
- スレッドコンテキストの保存と復元

スレッドライブラリの例には、-Solaris用のSolarisTMスレッド、Linuxで実装されているPOSIXスレッド、WindowsNTおよびWindows2000で使用可能なWin32スレッド、および標準のJavaTM Development Kit（JDK）の一部としてのJavaTMスレッドが含まれます。

Distributed Shared Memory (DSM) Systems− DSMシステムは、ハードウェアのサポートなしで共有メモリプログラミングを実装するために、疎結合アーキテクチャ上に共有メモリの抽象化を作成します。これらは標準ライブラリを実装し、最新のオペレーティングシステムに存在する高度なユーザーレベルのメモリ管理機能を使用します。例としては、トレッドマークシステム、ムニン、IVY、シャスタ、ブラゾス、カシミアなどがあります。
Program Annotation Packages−これは、均一なメモリアクセス特性を持つアーキテクチャに実装されています。プログラム注釈パッケージの最も注目すべき例はOpenMPです。OpenMPは機能的な並列処理を実装しています。これは主にループの並列化に焦点を当てています。

共有メモリの概念は、共有メモリシステムの低レベルの制御を提供しますが、面倒で誤っている傾向があります。アプリケーションプログラミングよりもシステムプログラミングに適しています。

共有メモリプログラミングのメリット

グローバルアドレス空間は、メモリへのユーザーフレンドリーなプログラミングアプローチを提供します。
メモリがCPUに近いため、プロセス間のデータ共有は高速で均一です。
プロセス間のデータ通信を明確に指定する必要はありません。
プロセス通信のオーバーヘッドはごくわずかです。
学ぶのはとても簡単です。

共有メモリプログラミングのデメリット

持ち運びできません。
データの局所性の管理は非常に困難です。

メッセージパッシングモデル

メッセージパッシングは、分散メモリシステムで最も一般的に使用される並列プログラミングアプローチです。ここで、プログラマーは並列処理を決定する必要があります。このモデルでは、すべてのプロセッサに独自のローカルメモリユニットがあり、通信ネットワークを介してデータを交換します。

プロセッサは、メッセージパッシングライブラリを使用してプロセッサ間の通信を行います。送信されるデータに加えて、メッセージには次のコンポーネントが含まれています-

メッセージの送信元のプロセッサのアドレス。
送信側プロセッサのデータのメモリ位置の開始アドレス。
送信データのデータ型。
送信データのデータサイズ。
メッセージの送信先のプロセッサのアドレス。
受信プロセッサのデータのメモリ位置の開始アドレス。

プロセッサは、次のいずれかの方法で相互に通信できます。

ポイントツーポイント通信
集合的コミュニケーション
メッセージパッシングインターフェイス

ポイントツーポイント通信

ポイントツーポイント通信は、メッセージパッシングの最も単純な形式です。ここで、メッセージは、次の転送モードのいずれかによって送信プロセッサから受信プロセッサに送信できます。

Synchronous mode −次のメッセージは、メッセージの順序を維持するために、前のメッセージが配信されたという確認を受信した後にのみ送信されます。
Asynchronous mode −次のメッセージを送信するために、前のメッセージの配信確認の受信は必要ありません。

集合的コミュニケーション

集合通信には、メッセージパッシング用に3つ以上のプロセッサが含まれます。以下のモードは集合的なコミュニケーションを可能にします-

Barrier −通信に含まれるすべてのプロセッサが特定のボックを実行している場合、バリアモードが可能です（ barrier block）メッセージパッシング用。
Broadcast −放送には2つのタイプがあります−
- One-to-all −ここでは、1回の操作で1つのプロセッサが、他のすべてのプロセッサに同じメッセージを送信します。
- All-to-all −ここでは、すべてのプロセッサが他のすべてのプロセッサにメッセージを送信します。

ブロードキャストされるメッセージには、次の3つのタイプがあります。

Personalized −他のすべての宛先プロセッサに一意のメッセージが送信されます。
Non-personalized −すべての宛先プロセッサが同じメッセージを受信します。
Reduction −リダクションブロードキャストでは、グループ内の1つのプロセッサが、グループ内の他のすべてのプロセッサからすべてのメッセージを収集し、それらを1つのメッセージに結合して、グループ内の他のすべてのプロセッサがアクセスできるようにします。

メッセージパッシングのメリット

並列処理の低レベルの制御を提供します。
ポータブルです。
エラーが発生しにくい。
並列同期とデータ配布のオーバーヘッドが少なくなります。

メッセージパッシングのデメリット

並列共有メモリコードと比較して、メッセージパッシングコードは一般により多くのソフトウェアオーバーヘッドを必要とします。

メッセージパッシングライブラリ

メッセージパッシングライブラリはたくさんあります。ここでは、最もよく使用される2つのメッセージパッシングライブラリについて説明します。

メッセージパッシングインターフェイス（MPI）
Parallel Virtual Machine（PVM）

メッセージパッシングインターフェイス（MPI）

分散メモリシステム内のすべての並行プロセス間で通信を提供することは、普遍的な標準です。一般的に使用される並列コンピューティングプラットフォームのほとんどは、メッセージパッシングインターフェイスの少なくとも1つの実装を提供します。これは、と呼ばれる事前定義された関数のコレクションとして実装されています。library また、C、C ++、Fortranなどの言語から呼び出すことができます。MPIは、他のメッセージパッシングライブラリと比較して高速で移植性があります。

Merits of Message Passing Interface

共有メモリアーキテクチャまたは分散メモリアーキテクチャでのみ実行されます。
各プロセッサには独自のローカル変数があります。
大規模な共有メモリコンピュータと比較して、分散メモリコンピュータは安価です。

Demerits of Message Passing Interface

並列アルゴリズムには、さらにプログラミングの変更が必要です。
デバッグが難しい場合があります。そして
ノード間の通信ネットワークではうまく機能しません。

Parallel Virtual Machine（PVM）

PVMは、ポータブルなメッセージパッシングシステムであり、別々の異種ホストマシンを接続して単一の仮想マシンを形成するように設計されています。これは、単一の管理可能な並列コンピューティングリソースです。超伝導研究、分子動力学シミュレーション、マトリックスアルゴリズムなどの大規模な計算問題は、多くのコンピューターのメモリと総電力を使用することで、よりコスト効率よく解決できます。互換性のないコンピュータアーキテクチャのネットワークで、すべてのメッセージルーティング、データ変換、タスクスケジューリングを管理します。

Features of PVM

インストールと構成が非常に簡単です。
複数のユーザーが同時にPVMを使用できます。
1人のユーザーが複数のアプリケーションを実行できます。
それは小さなパッケージです。
C、C ++、Fortranをサポートします。
PVMプログラムの特定の実行について、ユーザーはマシンのグループを選択できます。
メッセージパッシングモデルですが、
プロセスベースの計算;
異種アーキテクチャをサポートします。

データ並列プログラミング

データ並列プログラミングモデルの主な焦点は、データセットに対して同時に操作を実行することです。データセットは、配列、ハイパーキューブなどのような構造に編成されています。プロセッサは、同じデータ構造に対して集合的に操作を実行します。各タスクは、同じデータ構造の異なるパーティションで実行されます。

すべてのアルゴリズムをデータの並列性の観点から指定できるわけではないため、制限があります。これが、データの並列処理が普遍的ではない理由です。

データ並列言語は、データの分解とプロセッサへのマッピングを指定するのに役立ちます。また、プログラマーがデータ（たとえば、どのデータがどのプロセッサーに送られるか）を制御して、プロセッサー内の通信量を減らすことができるデータ分散ステートメントも含まれています。

アルゴリズムを適切に適用するには、適切なデータ構造を選択することが非常に重要です。これは、データ構造に対して実行される特定の操作が、別のデータ構造に対して実行される同じ操作と比較して時間がかかる場合があるためです。

Example−配列を使用してセットのi^番目の要素にアクセスするには、一定の時間がかかる場合がありますが、リンクリストを使用すると、同じ操作を実行するために必要な時間が多項式になる場合があります。

したがって、データ構造の選択は、アーキテクチャと実行する操作のタイプを考慮して行う必要があります。

以下のデータ構造は、並列プログラミングで一般的に使用されます-

リンクリスト
Arrays
ハイパーキューブネットワーク

リンクリスト

リンクリストは、ポインタで接続された0個以上のノードを持つデータ構造です。ノードは、連続するメモリ位置を占有する場合と占有しない場合があります。各ノードには2つまたは3つの部分があります-1つdata part データを保存し、他の2つは link fields前または次のノードのアドレスを格納します。最初のノードのアドレスは、と呼ばれる外部ポインタに格納されますhead。として知られている最後のノードtail, 通常、アドレスは含まれていません。

リンクリストには3つのタイプがあります-

単一リンクリスト
二重リンクリスト
循環リンクリスト

単一リンクリスト

単一リンクリストのノードには、データと次のノードのアドレスが含まれます。と呼ばれる外部ポインタhead 最初のノードのアドレスを格納します。

二重リンクリスト

二重リンクリストのノードには、前のノードと次のノードの両方のデータとアドレスが含まれています。と呼ばれる外部ポインタhead 最初のノードのアドレスと呼び出される外部ポインタを格納します tail 最後のノードのアドレスを格納します。

循環リンクリスト

循環リンクリストは、最後のノードが最初のノードのアドレスを保存したという事実を除いて、単一リンクリストと非常によく似ています。

配列

配列は、同様のタイプのデータを格納できるデータ構造です。1次元または多次元にすることができます。配列は静的または動的に作成できます。

に statically declared arrays, 配列の次元とサイズは、コンパイル時にわかっています。
に dynamically declared arrays, 配列の次元とサイズは実行時に認識されます。

共有メモリプログラミングの場合、配列は共通メモリとして使用でき、データ並列プログラミングの場合は、サブ配列に分割して使用できます。

ハイパーキューブネットワーク

ハイパーキューブアーキテクチャは、各タスクが他のタスクと通信する必要がある並列アルゴリズムに役立ちます。ハイパーキューブトポロジは、リングやメッシュなどの他のトポロジを簡単に埋め込むことができます。n-cubesとも呼ばれ、ここでnは次元数です。ハイパーキューブは再帰的に構築できます。

並列アルゴリズムの適切な設計手法を選択することは、最も困難で重要なタスクです。並列プログラミングの問題のほとんどには、複数の解決策がある場合があります。この章では、並列アルゴリズムの次の設計手法について説明します。

分割統治
欲張り法
動的計画法
Backtracking
分枝限定法
線形計画

分割統治法

分割統治法では、問題はいくつかの小さなサブ問題に分割されます。次に、サブ問題が再帰的に解決され、組み合わされて、元の問題の解決策が得られます。

分割統治法には、各レベルで次の手順が含まれます。

Divide −元の問題はサブ問題に分けられます。
Conquer −サブ問題は再帰的に解決されます。
Combine −サブ問題の解決策を組み合わせて、元の問題の解決策を取得します。

分割統治アプローチは、次のアルゴリズムで適用されます-

二分探索
クイックソート
マージソート
整数の乗算
逆行列
行列の乗算

欲張り法

ソリューションを最適化する欲張りアルゴリズムでは、いつでも最適なソリューションが選択されます。欲張りアルゴリズムは、複雑な問題に非常に簡単に適用できます。次のステップで最も正確なソリューションを提供するステップを決定します。

このアルゴリズムはと呼ばれます greedy小さいインスタンスに対する最適なソリューションが提供される場合、アルゴリズムはプログラム全体を考慮しないためです。解決策が検討されると、欲張りアルゴリズムは同じ解決策を再度検討することはありません。

欲張りアルゴリズムは、可能な限り最小のコンポーネントパーツからオブジェクトのグループを再帰的に作成します。再帰は、特定の問題の解決策がその問題のより小さなインスタンスの解決策に依存している問題を解決するための手順です。

動的計画法

動的計画法は、問題をより小さなサブ問題に分割する最適化手法であり、各サブ問題を解決した後、動的計画法はすべてのソリューションを組み合わせて最終的なソリューションを取得します。分割統治法とは異なり、動的計画法はサブ問題の解を何度も再利用します。

フィボナッチ数列の再帰的アルゴリズムは、動的計画法の一例です。

バックトラッキングアルゴリズム

バックトラッキングは、組み合わせの問題を解決するための最適化手法です。これは、プログラムによる問題と実際の問題の両方に適用されます。エイトクイーンの問題、数独パズル、迷路の通過は、バックトラッキングアルゴリズムが使用される人気のある例です。

バックトラックでは、必要なすべての条件を満たす可能な解決策から始めます。次に、次のレベルに移動し、そのレベルで満足のいく解決策が得られない場合は、1つのレベルに戻って、新しいオプションから始めます。

分枝限定法

分枝限定アルゴリズムは、問題の最適解を得るための最適化手法です。ソリューションの空間全体で、特定の問題に最適なソリューションを探します。最適化される関数の境界は、最新の最良のソリューションの値とマージされます。これにより、アルゴリズムは解空間の一部を完全に見つけることができます。

分枝限定法の目的は、ターゲットへの最低コストのパスを維持することです。解決策が見つかると、解決策を改善し続けることができます。分枝限定法は、深さ限定検索と深さ優先探索で実装されます。

線形計画

線形計画法は、最適化基準と制約の両方が線形関数である幅広いクラスの最適化ジョブを記述します。これは、最大の利益、最短経路、最小のコストなどの最良の結果を得るための手法です。

このプログラミングでは、変数のセットがあり、線形方程式のセットを満たし、特定の線形目的関数を最大化または最小化するために、変数に絶対値を割り当てる必要があります。

行列は、固定数の行と列に配置された数値データと非数値データのセットです。行列の乗算は、並列計算における重要な乗算設計です。ここでは、メッシュやハイパーキューブなどのさまざまな通信ネットワークでの行列乗算の実装について説明します。メッシュとハイパーキューブはネットワーク接続性が高いため、リングネットワークなどの他のネットワークよりも高速なアルゴリズムが可能です。

メッシュネットワーク

ノードのセットがp次元グリッドを形成するトポロジは、メッシュトポロジと呼ばれます。ここでは、すべてのエッジがグリッド軸に平行であり、隣接するすべてのノードが相互に通信できます。

ノードの総数=（行のノード数）×（列のノード数）

メッシュネットワークは、次の要素を使用して評価できます。

Diameter
二等分幅

Diameter −メッシュネットワークでは、最長 distance2つのノード間のはその直径です。を有するp次元メッシュネットワークkP ノードの直径は p(k–1)。

Bisection width −二等分幅は、メッシュネットワークを2つに分割するためにネットワークから削除する必要のあるエッジの最小数です。

メッシュネットワークを使用した行列の乗算

ラップアラウンド接続を持つ2DメッシュネットワークSIMDモデルを検討しました。我々は、N個の使用乗算2つのn×nの配列にアルゴリズムを設計する²時間の特定の量でプロセッサ。

行列AとBには、それぞれ要素_aijと_bijがあります。素子PEの処理_ijは表し_IJ及びB _IJを。すべてのプロセッサが乗算する要素のペアを持つように、行列AとBを配置します。行列Aの要素は左方向に移動し、行列Bの要素は上方向に移動します。行列AおよびBの要素の位置のこれらの変更は、各処理要素PE、乗算する新しい値のペアを示します。

アルゴリズムのステップ

2つの行列をずらします。
すべての製品を計算します_。aik × _bkj
手順2が完了したら合計を計算します。

アルゴリズム

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

ハイパーキューブネットワーク

超立方体は、エッジがそれらの間で垂直であり、同じ長さであるn次元構造です。n次元超立方体は、n立方体またはn次元立方体とも呼ばれます。

^2kノードのHypercubeの機能

直径= k
二等分幅= 2 ^k–1
エッジの数= k

Hypercubeネットワークを使用した行列の乗算

Hypercubeネットワークの一般仕様-

しましょう N = 2^mプロセッサの総数です。プロセッサはPとする_0、 P ₁ ... ..P _N-1。
IとIましょう^bは二つの整数、0 <I、Iであり^、B <N-1およびそのバイナリ表現は、B <K-1 <、位置Bのみが異なる0。
2つのn×n行列、行列Aと行列Bを考えてみましょう。
Step 1−行列Aと行列Bの要素は、位置i、j、kのプロセッサが_jiとb _ikを持つように、n3^個のプロセッサに割り当てられます。
Step 2 −位置（i、j、k）にあるすべてのプロセッサが積を計算します

C（i、j、k）= A（i、j、k）×B（i、j、k）
Step 3 −0≤i≤n-1の場合の合計C（0、j、k）=ΣC（i、j、k）。ここで、0≤j、k <n–1です。

ブロックマトリックス

ブロック行列または区分行列は、各要素自体が個々の行列を表す行列です。これらの個々のセクションは、block または sub-matrix。

例

図（a）では、Xはブロック行列であり、A、B、C、Dはそれ自体が行列です。図（f）は、マトリックス全体を示しています。

ブロック行列の乗算

2つのブロック行列が正方行列の場合、単純な行列乗算を実行するのと同じ方法で乗算されます。例えば、

並べ替えは、グループ内の要素を特定の順序、つまり昇順、降順、アルファベット順などに配置するプロセスです。ここでは、次のことについて説明します。

列挙型ソート
奇数偶数転置ソート
並列マージソート
ハイパークイックソート

要素のリストの並べ替えは、非常に一般的な操作です。大量のデータを並べ替える必要がある場合、順次並べ替えアルゴリズムは十分に効率的ではない可能性があります。したがって、ソートには並列アルゴリズムが使用されます。

列挙型ソート

列挙型ソートは、ソートされたリスト内の各要素の最終的な位置を見つけることによって、リスト内のすべての要素を配置する方法です。これは、各要素を他のすべての要素と比較し、値が小さい要素の数を見つけることによって行われます。

したがって、任意の2つの要素、_aiと_jについて、次のいずれかの場合が真でなければなりません。

a _i <a _j
a _i > a _j
a _i = a _j

アルゴリズム

procedure ENUM_SORTING (n)

begin
   for each process P_1,j do
      C[j] := 0;
		
   for each process P_{i, j} do
	
      if (A[i] < A[j]) or A[i] = A[j] and i < j) then
         C[j] := 1;
      else
         C[j] := 0;
			
   for each process P1, j do
      A[C[j]] := A[j];
		
end ENUM_SORTING

奇数偶数転置ソート

奇数偶数転置ソートは、バブルソート手法に基づいています。隣接する2つの番号を比較し、最初の番号が2番目の番号より大きい場合はそれらを切り替えて、昇順リストを取得します。逆の場合は、降順の系列に適用されます。奇数-偶数転置ソートは2つのフェーズで動作します-odd phase そして even phase。両方のフェーズで、プロセスは右側の隣接する番号と番号を交換します。

アルゴリズム

procedure ODD-EVEN_PAR (n) 

begin 
   id := process's label 
	
   for i := 1 to n do 
   begin 
	
      if i is odd and id is odd then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
      if i is even and id is even then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
   end for
	
end ODD-EVEN_PAR

並列マージソート

マージソートは、最初にソートされていないリストを可能な限り最小のサブリストに分割し、隣接リストと比較して、ソートされた順序でマージします。分割統治アルゴリズムに従うことにより、並列処理を非常にうまく実装します。

アルゴリズム

procedureparallelmergesort(id, n, data, newdata)

begin
   data = sequentialmergesort(data)
	
      for dim = 1 to n
         data = parallelmerge(id, dim, data)
      endfor
		
   newdata = data
end

ハイパークイックソート

ハイパークイックソートは、ハイパーキューブでのクイックソートの実装です。その手順は次のとおりです-

ソートされていないリストを各ノードに分割します。
各ノードをローカルで並べ替えます。
ノード0から、中央値をブロードキャストします。
各リストをローカルで分割してから、最も高い次元で半分を交換します。
寸法が0に達するまで、手順3と4を並行して繰り返します。

アルゴリズム

procedure HYPERQUICKSORT (B, n)
begin

   id := process’s label;
	
   for i := 1 to d do
      begin
      x := pivot;
      partition B into B1 and B2 such that B1 ≤ x < B2;
      if ith bit is 0 then
		
      begin
         send B2 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B1 U C;
      endif
      
      else
         send B1 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B2 U C;
         end else
      end for
		
   sort B using sequential quicksort;
	
end HYPERQUICKSORT

検索は、コンピュータサイエンスの基本的な操作の1つです。これは、要素が指定されたリストにあるかどうかを確認する必要があるすべてのアプリケーションで使用されます。この章では、次の検索アルゴリズムについて説明します。

分割統治
深さ優先探索
幅優先探索
最良優先探索

分割統治

分割統治法には、各レベルで次の手順が含まれます。

Divide −元の問題はサブ問題に分けられます。
Conquer −サブ問題は再帰的に解決されます。
Combine −サブ問題の解決策を組み合わせて、元の問題の解決策を取得します。

二分探索は分割統治アルゴリズムの一例です。

擬似コード

Binarysearch(a, b, low, high)

if low < high then
   return NOT FOUND
else
   mid ← (low+high) / 2
   if b = key(mid) then
      return key(mid)
   else if b < key(mid) then
      return BinarySearch(a, b, low, mid−1)
   else
   
      return BinarySearch(a, b, mid+1, high)

深さ優先探索

深さ優先探索（またはDFS）は、ツリーまたは無向グラフデータ構造を検索するためのアルゴリズムです。ここでの概念は、と呼ばれる開始ノードから開始することです。root同じブランチ内を可能な限りトラバースします。後続ノードのないノードを取得した場合は、まだアクセスされていない頂点に戻って続行します。

深さ優先探索のステップ

以前にアクセスされていないノード（ルート）を検討し、アクセス済みとしてマークします。
最初に隣接する後続ノードにアクセスし、アクセス済みとしてマークします。
検討対象のノードのすべての後続ノードがすでにアクセスされている場合、または後続ノードがもうない場合は、その親ノードに戻ります。

擬似コード

しましょう v グラフで検索を開始する頂点になります G。

DFS(G,v)

   Stack S := {};
	
   for each vertex u, set visited[u] := false;
   push S, v;
   while (S is not empty) do
     u := pop S;
	  
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbour w of u
            push S, w;
      end if
		
   end while
   
END DFS()

幅優先探索

幅優先探索（またはBFS）は、ツリーまたは無向グラフデータ構造を検索するためのアルゴリズムです。ここでは、ノードから始めて、同じレベルの隣接するすべてのノードにアクセスし、次のレベルの隣接する後続ノードに移動します。これは、level-by-level search。

幅優先探索のステップ

ルートノードから開始し、アクセス済みとしてマークします。
ルートノードには同じレベルのノードがないため、次のレベルに進みます。
隣接するすべてのノードにアクセスし、アクセス済みとしてマークします。
次のレベルに移動し、未訪問の隣接ノードすべてにアクセスします。
すべてのノードにアクセスするまで、このプロセスを続けます。

擬似コード

しましょう v グラフで検索を開始する頂点になります G。

BFS(G,v)

   Queue Q := {};
	
   for each vertex u, set visited[u] := false;
   insert Q, v;
   while (Q is not empty) do
      u := delete Q;
		
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbor w of u
            insert Q, w;
      end if
		
   end while
   
END BFS()

最良優先探索

最良優先探索は、グラフをトラバースして、可能な限り最短のパスでターゲットに到達するアルゴリズムです。BFSやDFSとは異なり、最良優先探索は評価関数に従って、次にトラバースするのに最も適切なノードを決定します。

最良優先探索のステップ

ルートノードから開始し、アクセス済みとしてマークします。
次に適切なノードを見つけて、訪問したことをマークします。
次のレベルに移動し、適切なノードを見つけて、アクセスしたことをマークします。
目標に到達するまでこのプロセスを続けます。

擬似コード

BFS( m )

   Insert( m.StartNode )
   Until PriorityQueue is empty
      c ← PriorityQueue.DeleteMin
      If c is the goal
      Exit
   Else
   
      Foreach neighbor n of c
         If n "Unvisited"
            Mark n "Visited"
            Insert( n )
      Mark c "Examined"
      
End procedure

グラフは、オブジェクトのペア間の接続を表すために使用される抽象表記です。グラフは次のもので構成されます-

Vertices−グラフ内の相互接続されたオブジェクトは、頂点と呼ばれます。頂点は、nodes。
Edges −エッジは、頂点を接続するリンクです。

グラフには2つのタイプがあります-

Directed graph −有向グラフでは、エッジには方向があります。つまり、エッジはある頂点から別の頂点に移動します。
Undirected graph −無向グラフでは、エッジに方向がありません。

グラフ彩色

グラフ彩色は、グラフの頂点に色を割り当てて、隣接する2つの頂点が同じ色にならないようにする方法です。いくつかのグラフ彩色の問題は次のとおりです。

Vertex coloring −隣接する2つの頂点が同じ色を共有しないように、グラフの頂点に色を付ける方法。
Edge Coloring −これは、隣接する2つのエッジが同じ色にならないように各エッジに色を割り当てる方法です。
Face coloring −平面グラフの各面または領域に色を割り当てて、共通の境界を共有する2つの面が同じ色にならないようにします。

彩色数

彩色数は、グラフに色を付けるために必要な最小色数です。たとえば、次のグラフの彩色数は3です。

グラフ彩色の概念は、時刻表の作成、移動無線周波数の割り当て、数独、レジスタ割り当て、およびマップの着色に適用されます。

グラフ彩色の手順

n次元配列の各プロセッサの初期値を1に設定します。
次に、特定の色を頂点に割り当てるために、その色が隣接する頂点にすでに割り当てられているかどうかを判別します。
プロセッサが隣接する頂点で同じ色を検出すると、配列内の値を0に設定します。
n ^2回の比較を行った後、配列のいずれかの要素が1の場合、それは有効な色付けです。

グラフ彩色の擬似コード

begin

   create the processors P(i₀,i₁,...i_n-1) where 0_i_v < m, 0 _ v < n
   status[i0,..i_n-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if a_j,k=1 and i_j=i_kthen
            status[i₀,..i_n-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

最小スパニングツリー

すべてのエッジの重み（または長さ）の合計がグラフGの他のすべての可能なスパニングツリーよりも小さいスパニングツリーは、として知られています。 minimal spanning tree または minimum cost spanning木。次の図は、加重連結グラフを示しています。

上記のグラフのいくつかの可能な全域木を以下に示します-

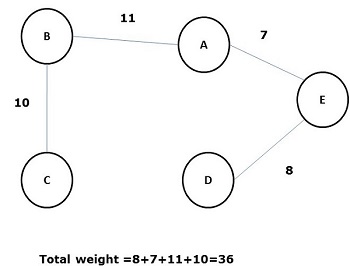
上記のすべての全域木のうち、図（d）は最小全域木です。最小コストスパニングツリーの概念は、巡回セールスマン問題、電子回路の設計、効率的なネットワークの設計、および効率的なルーティングアルゴリズムの設計に適用されます。

最小コストスパニングツリーを実装するには、次の2つの方法を使用します。

プリムのアルゴリズム
クラスカルのアルゴリズム

プリムのアルゴリズム

プリムのアルゴリズムは欲張りアルゴリズムであり、重み付き無向グラフの最小全域木を見つけるのに役立ちます。最初に頂点を選択し、その頂点に入射する重みが最も小さいエッジを見つけます。

プリムのアルゴリズムのステップ

任意の頂点を選択し、V言う₁グラフGのを
エッジを選択し、E言う₁ GのようなEその₁ = V ₁、V ₂及びV ₁ ≠V ₂及びE _1は、 Vのエッジ入射うち最小量を有する₁グラフGに
次に、ステップ2以下、V上の最小の重み付きエッジ入射選択₂。
n–1個のエッジが選択されるまでこれを続けます。ここにn は頂点の数です。

最小全域木は−です

クラスカルのアルゴリズム

クラスカルのアルゴリズムは欲張りアルゴリズムであり、接続された重み付きグラフの最小全域木を見つけるのに役立ち、各ステップでコストアークが増加します。これは、フォレスト内の任意の2つのツリーを接続する、可能な限り最小の重みのエッジを見つける最小スパニングツリーアルゴリズムです。

クラスカルのアルゴリズムのステップ

最小重量のエッジを選択します。E言う₁グラフGのとE _1がループではありません。
Eに接続されている次の最小重み付きエッジを選択₁。
n–1個のエッジが選択されるまでこれを続けます。ここにn は頂点の数です。

上のグラフの最小全域木は-です。

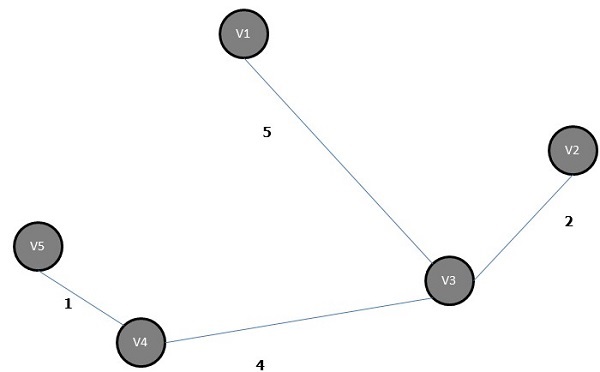
最短経路アルゴリズム

最短経路アルゴリズムは、送信元ノード（S）から宛先ノード（D）への最小コストのパスを見つける方法です。ここでは、幅優先探索アルゴリズムとしても知られるムーアのアルゴリズムについて説明します。

ムーアのアルゴリズム

ソース頂点Sにラベルを付け、ラベルを付けます i とセット i=0。
ラベルの付いた頂点に隣接するすべてのラベルのない頂点を検索します i。頂点Sに接続されている頂点がない場合、頂点DはSに接続されていません。Sに接続されている頂点がある場合は、それらにラベルを付けます。i+1。
Dにラベルが付いている場合は、手順4に進みます。そうでない場合は、手順2に進んでi = i +1を増やします。
最短経路の長さが見つかったら停止します。