数直線上に有理数をプロットする

定義

有理数は分数であり、次のように数直線上にプロットされます。

Basic rules of representing rational no. on number line

有理数（分数）が適切である場合、それは0と1の間にあります。
有理数（分数）が不適切な場合は、最初に混合分数に変換し、次に指定された有理数に変換します。整数と次の整数の間にあります。

次の手順を使用して、有理数または分数を表します。たとえば、数直線上の$ \ frac {5} {7} $です。

Step 1 −数直線を描きます。

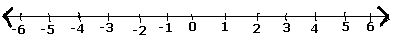
Step 2−数値$ \ frac {5} {7} $は正の数であるため、ゼロの右側にあります。

Step 3−したがって、ゼロマークの後、$ \ frac {1} {7}、\：\ frac {2} {7}、\：\ frac {3} {7}、\：\ frac {4} {7 }、\：\ frac {5} {7}、\：\ frac {6} {7}、$および（$ \ frac {7} {7} $ = 1）。

Step 4−数直線上の有理数$ \ frac {5} {7} $は次のように表示されます。

例1：

下の数直線に$ \ frac {1} {4} $と$ 1 \ frac {2} {4} $をプロットします

解決

Step 1:

$ \ frac {1} {4} $（A）は0から1の間にあります。$ 1 \ frac {2} {4} $（B）は1から2の間にあります

Step 2:

分数の底が4であるため、各分割は4つの部分に分割されます。

$ \ frac {1} {4} $は0の後の最初のマークであるため、ポイントAは$ \ frac {1} {4} $を表します

$ 1 \ frac {2} {4} $は1に続く2番目のマークであるため、ポイントBは$ 1 \ frac {2} {4} $を表します。

例2：

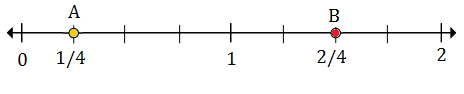
下の数直線に$ \ frac {5} {8} $と$ 2 \ frac {3} {8} $をプロットします

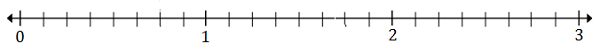
解決

Step 1:

$ \ frac {5} {8} $ 8（A）は0から1の間にあります。$ 2 \ frac {3} {8} $（B）は2から3の間にあります

Step 2:

分数の底が8であるため、各分割は8つの部分に分割されます。

$ \ frac {5} {8} $は0の後の5番目のマークであるため、ポイントAは$ \ frac {5} {8} $を表します

$ 2 \ frac {3} {8} $は2に続く3番目のマークであるため、ポイントBは$ 2 \ frac {3} {8} $を表します