AI-인기 검색 알고리즘

검색은 AI에서 문제를 해결하는 보편적 인 기술입니다. 타일 ​​게임, 스도쿠, 십자말 풀이 등과 같은 일부 싱글 플레이어 게임이 있습니다. 검색 알고리즘은 이러한 게임에서 특정 위치를 검색하는 데 도움이됩니다.

단일 에이전트 경로 찾기 문제

3X3 8 타일, 4X4 15 타일, 5X5 24 타일 퍼즐과 같은 게임은 단일 에이전트 경로 찾기 도전입니다. 빈 타일이있는 타일 매트릭스로 구성됩니다. 플레이어는 어떤 목표를 달성하기 위해 빈 공간에 수직 또는 수평으로 타일을 밀어 넣어 타일을 배열해야합니다.

단일 에이전트 길 찾기 문제의 다른 예는 Traveling Salesman Problem, Rubik 's Cube 및 Theorem Proving입니다.

용어 검색

• Problem Space− 검색이 이루어지는 환경입니다. (상태를 변경하기위한 일련의 상태 및 연산자 세트)

• Problem Instance − 초기 상태 + 목표 상태입니다.

• Problem Space Graph− 문제 상태를 나타냅니다. 상태는 노드로 표시되고 연산자는 가장자리로 표시됩니다.

• Depth of a problem − 초기 상태에서 목표 상태까지의 최단 경로 또는 최단 연산자 시퀀스의 길이.

• Space Complexity − 메모리에 저장되는 최대 노드 수.

• Time Complexity − 생성되는 최대 노드 수.

• Admissibility − 항상 최적의 솔루션을 찾기위한 알고리즘의 속성.

• Branching Factor − 문제 공간 그래프의 평균 자식 노드 수.

• Depth − 초기 상태에서 목표 상태까지의 최단 경로 길이.

무차별 대입 검색 전략

도메인 별 지식이 필요하지 않기 때문에 가장 간단합니다. 가능한 적은 수의 상태에서 잘 작동합니다.

요구 사항-

• 상태 설명
• 유효한 연산자 집합
• 초기 상태
• 목표 상태 설명

폭 우선 검색

루트 노드에서 시작하여 이웃 노드를 먼저 탐색하고 다음 레벨 이웃으로 이동합니다. 솔루션을 찾을 때까지 한 번에 하나의 트리를 생성합니다. FIFO 대기열 데이터 구조를 사용하여 구현할 수 있습니다. 이 방법은 솔루션에 대한 최단 경로를 제공합니다.

만약 branching factor(주어진 노드에 대한 평균 자식 노드 수) = b 및 깊이 = d, 수준 d = b ^d 의 노드 수 .

최악의 경우 생성 된 총 노드 수는 b + b ² + b ³ +… + b ^d 입니다.

Disadvantage− 다음 노드 생성을 위해 각 수준의 노드가 저장되므로 많은 메모리 공간을 소모합니다. 노드를 저장하는 데 필요한 공간은 기하 급수적입니다.

복잡성은 노드 수에 따라 다릅니다. 중복 노드를 확인할 수 있습니다.

깊이 우선 검색

LIFO 스택 데이터 구조를 사용하여 재귀로 구현됩니다. Breadth-First 방법과 동일한 노드 집합을 다른 순서로만 만듭니다.

단일 경로의 노드가 루트에서 리프 노드로의 각 반복에 저장되므로 노드를 저장하는 데 필요한 공간은 선형입니다. 분기 계수 b 및 깊이가 m 인 경우 저장 공간은 bm입니다.

Disadvantage−이 알고리즘은 종료되지 않고 한 경로에서 무한히 진행될 수 있습니다. 이 문제에 대한 해결책은 컷오프 깊이를 선택하는 것입니다. 이상적인 컷오프가 d 이고 선택한 컷오프가 d 보다 작 으면 이 알고리즘이 실패 할 수 있습니다. 선택한 컷오프가 d 보다 크면 실행 시간이 늘어납니다.

복잡성은 경로 수에 따라 다릅니다. 중복 노드는 확인할 수 없습니다.

양방향 검색

공통 상태를 식별하기 위해 둘 다 만날 때까지 초기 상태에서 앞으로 및 목표 상태에서 뒤로 검색합니다.

초기 상태의 경로는 목표 상태의 역 경로와 연결됩니다. 각 검색은 전체 경로의 최대 절반까지만 수행됩니다.

균일 비용 검색

정렬은 노드 경로의 비용 증가로 수행됩니다. 항상 최소 비용 노드를 확장합니다. 각 전환의 비용이 동일한 경우 Breadth First 검색과 동일합니다.

증가하는 비용 순서로 경로를 탐색합니다.

Disadvantage− 비용이 C * 이하인 긴 경로가 여러 개있을 수 있습니다. 균일 비용 검색은 모두를 탐색해야합니다.

반복 심화 깊이 우선 검색

레벨 1까지 깊이 우선 검색을 수행하고 처음부터 다시 시작하여 레벨 2까지 완전한 깊이 우선 검색을 실행하고 솔루션을 찾을 때까지 이러한 방식으로 계속합니다.

모든 하위 노드가 생성 될 때까지 노드를 생성하지 않습니다. 노드 스택 만 저장합니다. 알고리즘은 깊이 d 에서 해를 찾으면 종료됩니다 . 깊이 d 에서 생성 된 노드의 수 는 b ^d 이고 깊이 d-1 에서 생성되는 노드의 수 는 b ^{d-1입니다.}

다양한 알고리즘 복잡성 비교

다양한 기준에 따라 알고리즘의 성능을 살펴 보겠습니다.

표준	너비 우선	깊이 우선	양방향	균일 한 비용	인터랙티브 심화
시각	b d	b m	b d / 2	b d	b d
우주	b d	b m	b d / 2	b d	b d
최적 성	예	아니	예	예	예
완전성	예	아니	예	예	예

정보에 입각 한 (휴리스틱) 검색 전략

가능한 상태가 많은 큰 문제를 해결하려면 검색 알고리즘의 효율성을 높이기 위해 문제 별 지식을 추가해야합니다.

휴리스틱 평가 함수

두 주 사이의 최적 경로 비용을 계산합니다. 슬라이딩 타일 게임의 휴리스틱 함수는 각 타일이 목표 상태에서 이동하는 수를 계산하고 모든 타일에 대해 이러한 이동 수를 더하여 계산됩니다.

순수 휴리스틱 검색

휴리스틱 값 순서로 노드를 확장합니다. 이미 확장 된 노드에 대한 닫힌 목록과 생성되었지만 확장되지 않은 노드에 대한 열린 목록의 두 목록을 만듭니다.

각 반복에서 최소 휴리스틱 값이있는 노드가 확장되고 모든 하위 노드가 생성되어 닫힌 목록에 배치됩니다. 그런 다음 휴리스틱 기능이 자식 노드에 적용되고 휴리스틱 값에 따라 열린 목록에 배치됩니다. 짧은 경로는 저장되고 긴 경로는 삭제됩니다.

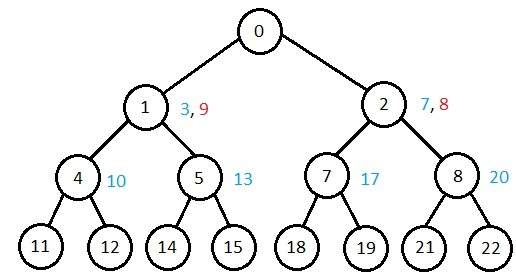
검색

가장 잘 알려진 형태의 Best First 검색입니다. 이미 비용이 많이 드는 경로 확장을 피하지만 가장 유망한 경로를 먼저 확장합니다.

f (n) = g (n) + h (n), 여기서

• g (n) 노드에 도달하기위한 비용 (지금까지)
• h (n) 노드에서 목표까지의 예상 비용
• f (n) n을 통해 목표에 이르는 경로의 총 예상 비용. f (n)을 증가시켜 우선 순위 큐를 사용하여 구현됩니다.

탐욕스러운 첫 번째 검색

목표에 가장 가까운 것으로 추정되는 노드를 확장합니다. f (n) = h (n)을 기반으로 노드를 확장합니다. 우선 순위 큐를 사용하여 구현됩니다.

Disadvantage− 루프에 갇힐 수 있습니다. 최적이 아닙니다.

지역 검색 알고리즘

그들은 예상 솔루션에서 시작하여 인접한 솔루션으로 이동합니다. 종료되기 전에 언제든지 중단 되더라도 유효한 솔루션을 반환 할 수 있습니다.

힐 클라이밍 검색

문제에 대한 임의의 솔루션으로 시작하여 솔루션의 단일 요소를 점진적으로 변경하여 더 나은 솔루션을 찾으려고 시도하는 반복 알고리즘입니다. 변경으로 더 나은 솔루션이 생성되면 점진적 변경이 새 솔루션으로 간주됩니다. 이 프로세스는 더 이상 개선되지 않을 때까지 반복됩니다.

기능 Hill-Climbing (문제)은 지역 최대 값 인 상태를 반환합니다.

inputs: problem, a problem
local variables: current, a node
                 neighbor, a node
current <-Make_Node(Initial-State[problem])
loop
   do neighbor <- a highest_valued successor of current
      if Value[neighbor] ≤ Value[current] then
      return State[current]
      current <- neighbor				  
	
end

Disadvantage −이 알고리즘은 완전하지도 최적도 아닙니다.

로컬 빔 검색

이 알고리즘에서는 주어진 시간에 k 개의 상태를 보유합니다. 처음에는 이러한 상태가 무작위로 생성됩니다. 이러한 k 상태의 후속 항목은 목적 함수의 도움으로 계산됩니다. 이러한 후속 작업 중 하나가 목적 함수의 최대 값이면 알고리즘이 중지됩니다.

그렇지 않으면 (초기 k 상태 및 상태의 후속 k 수 = 2k) 상태가 풀에 배치됩니다. 그런 다음 풀이 숫자로 정렬됩니다. 가장 높은 k 상태가 새로운 초기 상태로 선택됩니다. 이 프로세스는 최대 값에 도달 할 때까지 계속됩니다.

function BeamSearch ( problem, k )는 솔루션 상태를 반환합니다.

start with k randomly generated states
loop
   generate all successors of all k states
   if any of the states = solution, then return the state
   else select the k best successors
end

시뮬레이션 된 어닐링

어닐링은 금속을 가열 및 냉각하여 물리적 특성을 수정하기 위해 내부 구조를 변경하는 과정입니다. 금속이 냉각되면 새로운 구조가 포착되고 금속은 새로 얻은 특성을 유지합니다. 시뮬레이션 된 어닐링 공정에서 온도는 가변적으로 유지됩니다.

처음에는 온도를 높게 설정 한 다음 알고리즘이 진행됨에 따라 천천히 '냉각'되도록합니다. 온도가 높을 때 알고리즘은 높은 빈도로 더 나쁜 솔루션을 수용 할 수 있습니다.

스타트

• 초기화 k = 0; L = 정수 개수의 변수;
• i → j에서 성능 차이 Δ를 검색합니다.
• 만약 Δ <= 0이면 else if exp (-Δ / T (k))> random (0,1) then accept;
• L (k) 단계에 대해 1 단계와 2 단계를 반복합니다.
• k = k + 1;

기준이 충족 될 때까지 1-4 단계를 반복합니다.

종료

여행하는 세일즈맨 문제

이 알고리즘에서 목표는 도시에서 시작하여 모든 도시를 정확히 한 번 방문하고 동일한 시작 도시에서 끝나는 저렴한 여행을 찾는 것입니다.

Start
   Find out all (n -1)! Possible solutions, where n is the total number of cities.
   Determine the minimum cost by finding out the cost of each of these (n -1)! solutions.
   Finally, keep the one with the minimum cost.
end