컴퓨터의 기초-숫자 체계
숫자를 표현하고 작업하는 기술을 number system. Decimal number system가장 일반적인 숫자 체계입니다. 다른 인기있는 숫자 체계는 다음과 같습니다. binary number system, octal number system, hexadecimal number system, 기타
십진수 체계
십진수 체계는 base 100부터 9까지의 10 자리 숫자 체계는이 10 자리 숫자를 사용하여 모든 숫자를 나타낼 수 있음을 의미합니다. 십진수 시스템도positional value system. 이것은 숫자 값이 위치에 따라 달라진다는 것을 의미합니다. 이것을 이해하기 위해 예를 들어 보겠습니다.
734, 971, 207의 세 숫자가 있다고 가정 해 보겠습니다. 세 숫자 모두에서 7의 값이 다릅니다.
- 734에서 7의 값은 700 또는 700 또는 7 × 100 또는 7 × 10 2입니다.
- 971에서 7의 값은 7 수십 또는 70 또는 7 × 10 또는 7 × 10 1입니다.
- 207에서, 값 0F 7 7 개 단위 또는 7 × 7 × 7 1 10 0
각 위치의 가중치는 다음과 같이 나타낼 수 있습니다.

디지털 시스템에서는 전기 신호를 통해 지침이 제공됩니다. 변화는 신호의 전압을 변화시킴으로써 이루어집니다. 디지털 장비에서 10 진수 시스템을 구현하기 위해 10 가지 전압을 갖는 것은 어렵습니다. 따라서 디지털 방식으로 구현하기 쉬운 많은 숫자 체계가 개발되었습니다. 자세히 살펴 보겠습니다.
이진수 시스템
전기 신호를 통해 명령을 변경하는 가장 쉬운 방법은 켜짐과 꺼짐의 두 상태 시스템입니다. On은 1로 표시되고 off는 0으로 표시되지만 0은 실제로 신호가 아니라 낮은 전압에서 신호입니다. 이 두 자리 (0과 1) 만있는 숫자 체계가 호출됩니다.binary number system.
각 이진수는 bit. 이진수 시스템은 또한 위치 값 시스템이며 여기에 표시된 것처럼 각 숫자는 2의 거듭 제곱으로 표현 된 값을 갖습니다.

이진수에서 가장 오른쪽의 숫자가 호출됩니다. least significant bit (LSB) 그리고 가장 왼쪽 숫자는 most significant bit (MSB).
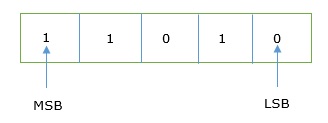
그리고이 숫자에 해당하는 십진수는 위치 값과 각 숫자의 곱의 합계입니다.
11010 (2) = 1 × 2 (4) + 1 × 2 3 + 0 2 × 2 + 1 × 2 (1) + 0 × 2 0
= 16 + 8 + 0 + 2 + 0
= 26 10
컴퓨터 메모리는 저장할 수있는 비트 수로 측정됩니다. 다음은 메모리 용량 변환 차트입니다.
- 1 바이트 (B) = 8 비트
- 1 킬로바이트 (KB) = 1024 바이트
- 1 메가 바이트 (MB) = 1024KB
- 1 기가 바이트 (GB) = 1024MB
- 1 테라 바이트 (TB) = 1024GB
- 1 엑사 바이트 (EB) = 1024PB
- 1 제타 바이트 = 1024EB
- 1 요타 바이트 (YB) = 1024ZB
8 진법
Octal number system 8 자리 숫자-0, 1, 2, 3, 4, 5, 6 및 7입니다. 8 진수 시스템은 또한 여기에 표시된 것처럼 각 숫자가 8의 거듭 제곱으로 표현되는 값을 갖는 위치 값 시스템입니다.

8 진수에 해당하는 10 진수는 각 숫자와 해당 위치 값의 곱의 합계입니다.
726 8 = 7 × 8 2 + 2 × 8 1 + 6 × 8 0
= 448 + 16 + 6
= 470 10
16 진수 시스템
Octal number system 16 개의 기호가 있습니다. 0에서 9까지, A에서 F까지, 여기서 A는 10, B는 11과 같은 식으로 F까지 계속됩니다. 16 진수 시스템은 또한 각 숫자가 16의 거듭 제곱으로 표현되는 값을 갖는 위치 값 시스템입니다. , 여기에 표시된대로-

16 진수에 해당하는 10 진수는 위치 값과 각 숫자의 곱의 합계입니다.
27FB 16 = 2 × 16 3 + 7 × 16 2 + 15 16 × 1 + 10 × 16 0
= 8192 + 1792 + 240 +10
= 10234 10
번호 체계 관계
다음 표는 10 진수, 2 진수, 8 진수 및 16 진수 시스템 간의 관계를 보여줍니다.
| 16 진법 | 소수 | 옥탈 | 바이너리 |
|---|---|---|---|
| 0 | 0 | 0 | 0000 |
| 1 | 1 | 1 | 0001 |
| 2 | 2 | 2 | 0010 |
| 삼 | 삼 | 삼 | 0011 |
| 4 | 4 | 4 | 0100 |
| 5 | 5 | 5 | 0101 |
| 6 | 6 | 6 | 0110 |
| 7 | 7 | 7 | 0111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| ㅏ | 10 | 12 | 1010 년 |
| 비 | 11 | 13 | 1011 |
| 씨 | 12 | 14 | 1100 년 |
| 디 | 13 | 15 | 1101 |
| 이자형 | 14 | 16 | 1110 년 |
| 에프 | 15 | 17 | 1111 년 |
ASCII
숫자 데이터 외에도 컴퓨터는 영어의 완전한 문자 집합을 형성하는 알파벳, 구두점, 수학 연산자, 특수 기호 등을 처리 할 수 있어야합니다. 전체 문자 또는 기호 집합을 영숫자 코드라고합니다. 완전한 영숫자 코드에는 일반적으로-
- 26 개의 대문자
- 26 개의 소문자
- 10 자리
- 7 개의 문장 부호
- 20 ~ 40 개의 특수 문자
이제 컴퓨터는 숫자 체계가 사용하는 숫자 값만 이해합니다. 따라서 모든 문자에는 영숫자 코드라고하는 동등한 숫자가 있어야합니다. 가장 널리 사용되는 영숫자 코드는 정보 교환을위한 미국 표준 코드 (ASCII)입니다. ASCII는 128 (27) 개의 가능한 코드가있는 7 비트 코드입니다.

ISCII
ISCII는 Indian Script Code for Information Interchange. IISCII는 컴퓨터에서 인도어를 지원하기 위해 개발되었습니다. IISCI에서 지원하는 언어에는 Devanagari, Tamil, Bangla, Gujarati, Gurmukhi, Tamil, Telugu 등이 포함됩니다. IISCI는 주로 정부 부서에서 사용하고 있으며 그 전에는 새로운 범용 인코딩 표준 인Unicode 소개되었습니다.
유니 코드
유니 코드는 다른 언어 스크립트와 함께 사용하도록 설계된 국제 코딩 시스템입니다. 각 문자 또는 기호에는 주로 ASCII 프레임 워크 내에서 고유 한 숫자 값이 할당됩니다. 이전에는 각 스크립트에 서로 충돌 할 수있는 자체 인코딩 시스템이있었습니다.
대조적으로 이것은 유니 코드가 공식적으로하고자하는 것입니다. 유니 코드는 플랫폼이 무엇이든, 프로그램이 무엇이든, 언어가 무엇이든 상관없이 모든 문자에 대해 고유 한 번호를 제공합니다 .