전자 회로-정류기

AC를 DC 전원으로 변환해야 할 때마다 정류기 회로가 구조를 위해 제공됩니다. 간단한 PN 접합 다이오드가 정류기 역할을합니다. 다이오드의 순방향 바이어스 및 역방향 바이어스 조건은 정류를 만듭니다.

정류

교류는 상태를 지속적으로 변경하는 속성을 가지고 있습니다. 이것은 교류가 표시되는 사인파를 관찰함으로써 이해됩니다. 양의 방향으로 상승하면 최고 양의 값으로 이동하고 거기에서 정상으로 감소하고 다시 음의 부분으로 이동하여 음의 피크에 도달하고 다시 정상으로 돌아와 계속됩니다.

파동 형성 과정에서 파동이 양의 방향과 음의 방향으로 진행되는 것을 볼 수 있습니다. 실제로 그것은 완전히 바뀌므로 이름이 교류입니다.

그러나 정류 과정 에서이 교류는 직류 DC로 변경됩니다. 그때까지 양의 방향과 음의 방향으로 흐르는 파동은 DC로 변환 될 때 방향이 양의 방향으로 만 제한됩니다. 따라서 전류는 아래 그림과 같이 양의 방향으로 만 흐르고 음의 방향으로 저항합니다.

정류를하는 회로를 Rectifier circuit. 다이오드는 정류기로 사용되어 정류기 회로를 구성합니다.

정류기 회로의 유형

출력에 따라 두 가지 주요 유형의 정류기 회로가 있습니다. 그들은

반파 정류기
전파 정류기

반파 정류기 회로는 입력 전원의 양의 반 주기만 정류하는 반면, 전파 정류기 회로는 입력 전원의 양과 음의 반주기를 모두 정류합니다.

반파 정류기

이름 반파 정류기 자체는 rectification 에 대해서만 수행됩니다 half주기의. AC 신호는 용도에 따라 상승 또는 하강하는 입력 변압기를 통해 제공됩니다. 입력 전압을 낮추기 위해 대부분 강압 변압기가 정류기 회로에 사용됩니다.

변압기에 주어진 입력 신호는 정류기 역할을하는 PN 접합 다이오드를 통해 전달됩니다. 이 다이오드는 입력의 양의 반주기 동안 만 AC 전압을 맥동 DC로 변환합니다. 부하 저항은 회로 끝에 연결됩니다. 아래 그림은 반파 정류기의 회로를 보여줍니다.

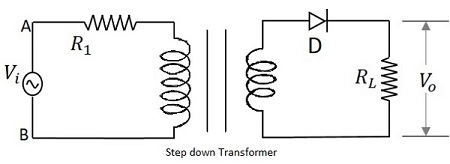
HWR의 작동

입력 신호는 전압 레벨을 감소시키는 변압기에 제공됩니다. 변압기의 출력은 정류기 역할을하는 다이오드에 제공됩니다. 이 다이오드는 입력 신호의 양의 반주기 동안 ON (전도)됩니다. 따라서 전류가 회로에 흐르고 부하 저항에서 전압 강하가 발생합니다. 다이오드는 음의 반주기 동안 OFF (전도하지 않음)가되므로 음의 반주기에 대한 출력은 $ i_ {D} = 0 $ 및 $ V_ {o} = 0 $가됩니다.

따라서 출력은 입력 전압의 양의 반주기 동안 만 존재합니다 (역 누설 전류 무시). 이 출력은 부하 저항을 가로 지르는 맥동이됩니다.

HWR의 파형

입력 및 출력 파형은 다음 그림과 같습니다.

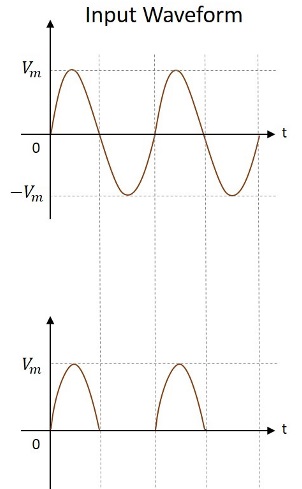
따라서 반파 정류기의 출력은 맥동 DC입니다. 반파 정류기의 출력에서 얻은 몇 가지 값을 이해하여 위의 회로를 분석해 보겠습니다.

반파 정류기 분석

반파 정류기 회로를 분석하기 위해 입력 전압 방정식을 고려해 보겠습니다.

$$ v_ {i} = V_ {m} \ sin \ omega t $$

$ V_ {m} $는 공급 전압의 최대 값입니다.

다이오드가 이상적이라고 가정합시다.

순방향, 즉 ON 상태의 저항은 $ R_f $입니다.
반대 방향, 즉 OFF 상태의 저항은 $ R_r $입니다.

현재 i 다이오드 또는 부하 저항 $ R_L $에서

$ i = I_m \ sin \ omega t \ quad for \ quad 0 \ leq \ omega t \ leq 2 \ pi $

$ i = 0 \ quad \ quad \ quad \ quad for \ quad \ pi \ leq \ omega t \ leq 2 \ pi $

어디

$$ I_m = \ frac {V_m} {R_f + R_L} $$

DC 출력 전류

현재 평균 $ I_ {dc} $는 다음과 같습니다.

$$ I_ {dc} = \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i \ : d \ left (\ omega t \ right) $$

$$ = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} I_m \ sin \ omega t \ : d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0 \ : d \ left (\ omega t \ right) \ right] $$

$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {-\ cos \ omega t \ right \} _ {0} ^ {\ pi} \ right] $$

$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {+ 1- \ left (-1 \ right) \ right \} \ right] = \ frac {I_m} {\ pi} = 0.318 I_m $$

$ I_m $ 값을 대체하면

$$ I_ {dc} = \ frac {V_m} {\ pi \ left (R_f + R_L \ right)} $$

$ R_L >> R_f $이면

$$ I_ {dc} = \ frac {V_m} {\ pi R_L} = 0.318 \ frac {V_m} {R_L} $$

DC 출력 전압

DC 출력 전압은 다음과 같습니다.

$$ V_ {dc} = I_ {dc} \ times R_L = \ frac {I_m} {\ pi} \ times R_L $$

$$ = \ frac {V_m \ times R_L} {\ pi \ left (R_f + R_L \ right)} = \ frac {V_m} {\ pi \ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$

$ R_L >> R_f $이면

$$ V_ {dc} = \ frac {V_m} {\ pi} = 0.318V_m $$

RMS 전류 및 전압

RMS 전류의 값은 다음과 같습니다.

$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i ^ {2} d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} I_ {m} ^ {2} \ sin ^ {2} \ omega t \ : d \ left (\ omega t \ right) + \ frac {1} {2 \ pi} \ int _ {\ pi} ^ {2 \ pi} 0 \ : d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {2 \ pi} \ int_ {0} ^ {\ pi} \ left (\ frac {1- \ cos 2 \ omega t} {2 } \ 오른쪽) d \ 왼쪽 (\ omega t \ 오른쪽) \ 오른쪽] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ left (\ omega t \ right)-\ frac {\ sin 2 \ omega t} {2} \ 오른쪽 \} _ {0} ^ {\ pi} \ 오른쪽] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ pi-0-\ frac {\ sin 2 \ pi} {2} + \ sin 0 \ right \} \ 오른쪽] ^ {\ frac {1} {2}} $$

$$ = \ 왼쪽 [\ frac {I_ {m} ^ {2}} {4 \ pi} \ right] ^ {\ frac {1} {2}} = \ frac {I_m} {2} $$

$$ = \ frac {V_m} {2 \ 왼쪽 (R_f + R_L \ 오른쪽)} $$

부하 양단의 RMS 전압은

$$ V_ {rms} = I_ {rms} \ times R_L = \ frac {V_m \ times R_L} {2 \ left (R_f + R_L \ right)} $$

$$ = \ frac {V_m} {2 \ 왼쪽 \ {1+ \ 왼쪽 (R_f / R_L \ 오른쪽) \ 오른쪽 \}} $$

$ R_L >> R_f $이면

$$ V_ {rms} = \ frac {V_m} {2} $$

정류기 효율

모든 회로는 더 나은 출력을 위해 효율적으로 작동해야합니다. 반파 정류기의 효율을 계산하려면 입력 전력에 대한 출력 전력의 비율을 고려해야합니다.

정류기 효율은 다음과 같이 정의됩니다.

$$ \ eta = \ frac {dcpower \ : \ : 전달됨 \ : \ : to \ : \ : the \ : \ : load} {acinput \ : \ : power \ : \ : from \ : \ : transformer \ : \ : secondary} = \ frac {P_ {ac}} {P_ {dc}} $$

지금

$$ P_ {dc} = \ left ({I_ {dc}} \ right) ^ 2 \ times R_L = \ frac {I_m R_L} {\ pi ^ 2} $$

더욱이

$$ P_ {ac} = P_a + P_r $$

어디

$ P_a = 전력 \ : 소산 \ : at \ : \ : 접합 \ : of \ : 다이오드 $

$$ = I_ {rms} ^ {2} \ times R_f = \ frac {I_ {m} ^ {2}} {4} \ times R_f $$

과

$$ P_r = 전력 \ : 소산 \ : in \ : 부하 \ : 저항 $$

$$ = I_ {rms} ^ {2} \ times R_L = \ frac {I_ {m} ^ {2}} {4} \ times R_L $$

$$ P_ {ac} = \ frac {I_ {m} ^ {2}} {4} \ times R_f + \ frac {I_ {m} ^ {2}} {4} \ times R_L = \ frac {I_ {m } ^ {2}} {4} \ 왼쪽 (R_f + R_L \ 오른쪽) $$

$ P_ {ac} $ 및 $ P_ {dc} $의 표현식 모두에서 다음과 같이 작성할 수 있습니다.

$$ \ eta = \ frac {I_ {m} ^ {2} R_L / \ pi ^ 2} {I_ {m} ^ {2} \ left (R_f + R_L \ right) / 4} = \ frac {4} {\ pi ^ 2} \ frac {R_L} {\ left (R_f + R_L \ right)} $$

$$ = \ frac {4} {\ pi ^ 2} \ frac {1} {\ left \ {1+ \ left (R_f / R_L \ right) \ right \}} = \ frac {0.406} {\ left \ {1+ \ 왼쪽 (R_f / R_L \ 오른쪽) \ 오른쪽 \}} $$

백분율 정류기 효율

$$ \ eta = \ frac {40.6} {\ lbrace1 + \ lgroup \ : R_ {f} / R_ {L} \ rgroup \ rbrace} $$

이론적으로 $ R_ {f} / R_ {L} = 0 $ 일 때 반파 정류기의 정류기 효율의 최대 값은 40.6 %입니다.

또한 효율은 다음과 같은 방법으로 계산할 수 있습니다.

$$ \ eta = \ frac {P_ {dc}} {P_ {ac}} = \ frac {\ left (I_ {dc} \ right) ^ 2R_L} {\ left (I_ {rms} \ right) ^ 2R_L} = \ frac {\ left (V_ {dc} / R_L \ right) ^ 2R_L} {\ left (V_ {rms} / R_L \ right) ^ 2R_L} = \ frac {\ left (V_ {dc} \ right) ^ 2} {\ 왼쪽 (V_ {rms} \ 오른쪽) ^ 2} $$

$$ = \ frac {\ left (V_m / \ pi \ right) ^ 2} {\ left (V_m / 2 \ right) ^ 2} = \ frac {4} {\ pi ^ 2} = 0.406 $$

$$ = 40.6 \ % $$

리플 팩터

정류 된 출력에는 잔물결 형태로 존재하는 일정량의 AC 구성 요소가 포함되어 있습니다. 이것은 반파 정류기의 출력 파형을 관찰함으로써 이해됩니다. 순수한 DC를 얻으려면이 구성 요소에 대한 아이디어가 필요합니다.

리플 팩터는 정류 된 출력의 물결 모양을 제공합니다. 다음과 같이 표시됩니다.y. 이것은 전압 또는 전류의 AC 구성 요소의 유효 값과 직접 값 또는 평균 값의 비율로 정의 할 수 있습니다.

$$ \ gamma = \ frac {ripple \ : voltage} {dc \ : voltage} = \ frac {rms \ : value \ : of \ : accomponent} {dcvalue \ : of \ : wave} = \ frac {\ left ( V_r \ 오른쪽) _ {rms}} {v_ {dc}} $$

여기,

$$ \ 왼쪽 (V_r \ 오른쪽) _ {rms} = \ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}} $$

따라서,

$$ \ gamma = \ frac {\ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}}} {V_ {dc}} = \ sqrt {\ left (\ frac {V_ {rms} } {V_ {dc}} \ right) ^ 2-1} $$

지금,

$$ V_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} V_ {m} ^ {2} \ sin ^ 2 \ omega t \ : d \ 왼쪽 (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ = V_m \ left [\ frac {1} {4 \ pi} \ int_ {0} ^ {\ pi} \ left (1- \ cos2 \ : \ omega t \ right) d \ left (\ omega t \ 오른쪽) \ right] ^ {\ frac {1} {2}} = \ frac {V_m} {2} $$

$$ V_ {dc} = V_ {av} = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} V_m \ sin \ omega t \ : d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0.d \ left (\ omega t \ right) \ right] $$

$$ = \ frac {V_m} {2 \ pi} \ left [-\ cos \ omega t \ right] _ {0} ^ {\ pi} = \ frac {V_m} {\ pi} $$

$$ \ gamma = \ sqrt {\ left [\ left \ {\ frac {\ left (V_m / 2 \ right)} {\ left (V_m / \ pi \ right)} \ right \} ^ 2-1 \ right ]} = \ sqrt {\ left \ {\ left (\ frac {\ pi} {2} \ right) ^ 2-1 \ right \}} = 1.21 $$

리플 계수는 다음과 같이 정의됩니다.

$$ \ gamma = \ frac {\ left (I_r \ right) _ {rms}} {I_ {dc}} $$

반파 정류기에 존재하는 리플 계수의 값이 1.21이므로 출력에 존재하는 AC의 양이 DC 전압의 $ 121 \ % $임을 의미합니다.

규제

부하를 통과하는 전류는 부하 저항에 따라 달라질 수 있습니다. 그러나 이러한 조건에서도 부하 저항에 걸리는 출력 전압이 일정 할 것으로 예상합니다. 따라서 다른 부하 조건에서도 전압을 조절해야합니다.

DC 부하 전류의 변화에 따른 DC 출력 전압의 변화는 다음과 같이 정의됩니다. Regulation. 비율 규정은 다음과 같이 계산됩니다.

$$ Percentage \ : regulation = \ frac {V_ {no \ : load} -V_ {full \ : load}} {V_ {full \ : load}} \ times 100 \ % $$

비율 조절이 낮을수록 전원 공급 장치가 더 좋습니다. 이상적인 전원 공급 장치는 0 % 조절을 갖습니다.

변압기 활용 계수

정류기 회로에서 부하로 전달되는 DC 전력은 회로에 사용되는 변압기의 정격을 결정합니다.

따라서 변압기 사용률은 다음과 같이 정의됩니다.

$$ TUF = \ frac {dcpower \ : to \ : be \ : delivered \ : to \ : the \ : load} {acrating \ : of \ : the \ : transformer \ : secondary} $$

$$ = \ frac {P_ {dc}} {P_ {ac \ left (\ right)}} $$

변압기 이론에 따르면 2 차측의 정격 전압은

$$ V_m / \ sqrt {2} $$

그것을 통해 흐르는 실제 RMS 전압은

$$ I_m / 2 $$

따라서

$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left (V_m / \ sqrt {2} \ right) \ times \ left (I_m / 2 \ right)} $ $

그러나

$$ V_m = I_m \ 왼쪽 (R_f + R_L \ 오른쪽) $$

따라서

$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left \ {I_m \ left (R_f + R_L \ right) / \ sqrt {2} \ right \} \ times \ 왼쪽 (I_m / 2 \ 오른쪽)} $$

$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} \ times \ frac {R_L} {\ left (R_f + R_L \ right)} $$

$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} = 0.287 $$

피크 역 전압

역 바이어스로 연결된 다이오드는 제어 된 전압 수준에서 작동해야합니다. 이 안전 전압을 초과하면 다이오드가 손상됩니다. 따라서 최대 전압에 대해 아는 것이 매우 중요합니다.

다이오드가 파괴되지 않고 견딜 수있는 최대 역 전압을 Peak Inverse Voltage. 요컨대PIV.

여기서 PIV는 Vm에 불과합니다.

폼 팩터

이것은 파형에있는 모든 지점의 절대 값에 대한 수학적 평균으로 이해할 수 있습니다. 그만큼form factorRMS 값과 평균 값의 비율로 정의됩니다. 다음과 같이 표시됩니다.F.

$$ F = \ frac {rms \ : value} {average \ : value} = \ frac {I_m / 2} {I_m / \ pi} = \ frac {0.5I_m} {0.318I_m} = 1.57 $$

피크 팩터

정류가 얼마나 효과적인지 알기 위해서는 잔물결의 피크 값을 고려해야합니다. 피크 팩터 값도 중요한 고려 사항입니다.Peak factor RMS 값에 대한 피크 값의 비율로 정의됩니다.

따라서

$$ Peak Factor = \ frac {Peak \ : value} {rms \ : value} = \ frac {V_m} {V_m / 2} = 2 $$

이 모든 것은 정류기에 대해 연구하는 동안 고려해야 할 중요한 매개 변수입니다.