전자 회로-신호

ㅏ Signal"생성 된 소스에있는 데이터에 대한 정보를 제공하는 표현"으로 이해할 수 있습니다. 이것은 일반적으로 시간에 따라 다릅니다. 따라서 신호는source of energy which transmits some information. 이것은 그래프로 쉽게 표현할 수 있습니다.

예

알람은 시간이되었음을 알려줍니다.
밥솥 휘슬이 음식이 조리되었음을 확인합니다.
빨간색 표시등은 위험을 나타냅니다.
교통 신호는 이동을 나타냅니다.
전화벨이 울립니다.

신호는 일부 정보를 전달하는 모든 유형이 될 수 있습니다. 전자 장비에서 생성 된이 신호를Electronic Signal 또는 Electrical Signal. 일반적으로 시간 변형입니다.

신호 유형

신호는 특성에 따라 아날로그 또는 디지털로 분류 할 수 있습니다. 다음 이미지와 같이 아날로그 및 디지털 신호를 더 자세히 분류 할 수 있습니다.

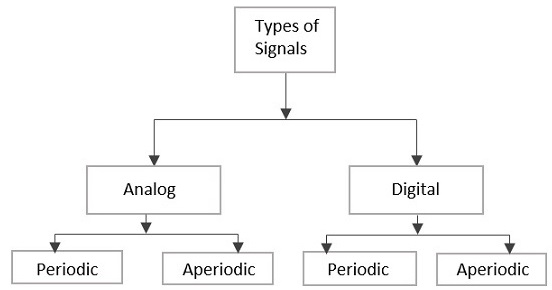
아날로그 신호

시간에 따라 변하는 양을 나타내는 연속적인 시변 신호는 다음과 같이 불릴 수 있습니다. Analog Signal. 이 신호는 그것을 나타내는 수량의 순간 값에 따라 시간에 따라 계속 변합니다.

디지털 신호

인 신호 discrete 본질적으로 또는 non-continuous 형태로 Digital signal. 이 신호에는 개별 값이 있으며, 개별 값은 특정 시점에서 파생 된 것처럼 이전 값을 기반으로하지 않습니다.

주기적 신호 및 비 주기적 신호

일정 기간 동안 패턴을 반복하는 아날로그 또는 디지털 신호를 Periodic Signal. 이 신호는 패턴이 반복적으로 계속되고 가정하거나 계산하기 쉽습니다.

일정 기간 동안 패턴을 반복하지 않는 아날로그 또는 디지털 신호를 Aperiodic Signal. 이 신호는 패턴이 계속되어 있지만 패턴이 반복되지 않으며 추정하거나 계산하기가 쉽지 않습니다.

신호 및 표기법

중 Periodic Signals가장 일반적으로 사용되는 신호는 사인파, 코사인 파, 삼각파, 구형파, 사각 파, 톱니파, 펄스 파형 또는 펄스열 등입니다. 이러한 파형을 살펴 보겠습니다.

단위 단계 신호

단위 단계 신호는 원점에서 X 축의 한 단위까지 한 단위의 값을 갖습니다. 이것은 주로 테스트 신호로 사용됩니다. 단위 스텝 신호의 이미지는 아래와 같습니다.

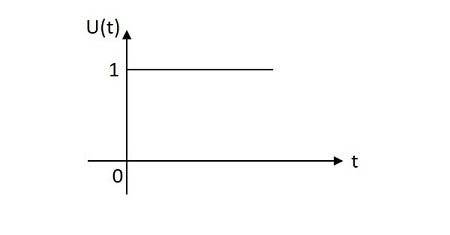
단위 단계 함수는 $ u \ left (t \ right) $로 표시됩니다. 그것은 다음과 같이 정의됩니다-

$$ u \ left (t \ right) = \ left \ {\ begin {matrix} 1 & t \ geq 0 \\ 0 & t <0 \ end {matrix} \ right. $$

단위 임펄스 신호

단위 임펄스 신호는 원점에서 한 단위의 값을 갖습니다. 그 면적은 하나의 단위입니다. 단위 임펄스 신호의 이미지는 아래와 같습니다.

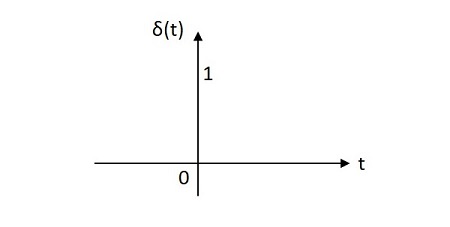
단위 임펄스 함수는 다음과 같이 표시됩니다. ẟ(t). 다음과 같이 정의됩니다.

$$ \ delta \ left (t \ right) = \ left \ {\ begin {matrix} \ infty \ : \ : if \ : \ : t = 0 \\ 0 \ : \ : if \ : \ : t \ neq 0 \ end {matrix} \ right. $$

$$ \ int _ {-\ infty} ^ {\ infty} \ delta \ left (t \ right) d \ left (t \ right) = 1 $$

$$ \ int _ {-\ infty} ^ {t} \ delta \ left (t \ right) d \ left (t \ right) = u \ left (t \ right) $$

$$ \ delta \ left (t \ right) = \ frac {du \ left (t \ right)} {d \ left (t \ right)} $$

단위 램프 신호

단위 램프 신호의 값은 원점에서 기하 급수적으로 증가합니다. 단위 램프 신호의 이미지는 아래와 같습니다.

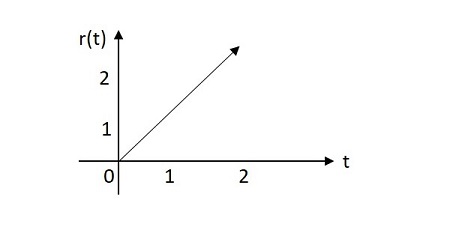
단위 램프 기능은 다음과 같이 표시됩니다. u(t). 그것은 다음과 같이 정의됩니다-

$$ \ int_ {0} ^ {t} u \ left (t \ right) d \ left (t \ right) = \ int_ {0} ^ {t} 1 dt = t = r \ left (t \ right) $$

$$ u \ 왼쪽 (t \ 오른쪽) = \ frac {dr \ 왼쪽 (t \ 오른쪽)} {dt} $$

단위 포물선 신호

단위 포물선 신호는 원점에서 포물선처럼 값이 변경됩니다. 단위 포물선 신호의 이미지는 아래와 같습니다.

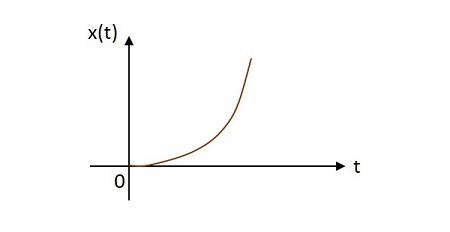
단위 포물선 함수는 $ u \ left (t \ right) $로 표시됩니다. 그것은 다음과 같이 정의됩니다-

$$ \ int_ {0} ^ {t} \ int_ {0} ^ {t} u \ left (t \ right) dtdt = \ int_ {0} ^ {t} r \ left (t \ right) dt = \ int_ {0} ^ {t} t.dt = \ frac {t ^ {2}} {2} dt = x \ left (t \ right) $$

$$ r \ 왼쪽 (t \ 오른쪽) = \ frac {dx \ 왼쪽 (t \ 오른쪽)} {dt} $$

$$ u \ 왼쪽 (t \ 오른쪽) = \ frac {d ^ {2} x \ 왼쪽 (t \ 오른쪽)} {dt ^ {2}} $$

Signum 기능

Signum 함수는 원점에서 양의 평면과 음의 평면에 균등하게 분포 된 값을 갖습니다. Signum 기능의 이미지는 아래와 같습니다.

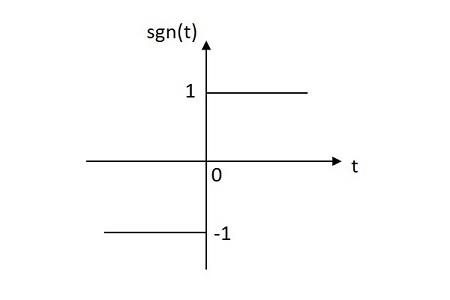
Signum 함수는 다음과 같이 표시됩니다. sgn(t). 다음과 같이 정의됩니다.

$$ sgn \ left (t \ right) = \ left \ {\ begin {matrix} 1 \ : \ : for \ : \ : t \ geq 0 \\-1 \ : \ : for \ : \ : t <0 \ end {matrix} \ right. $$

$$ sgn \ 왼쪽 (t \ 오른쪽) = 2u \ 왼쪽 (t \ 오른쪽) -1 $$

지수 신호

지수 신호는 원점에서 지수 적으로 변하는 값을 갖습니다. 지수 함수는 다음과 같습니다.

$$ x \ 왼쪽 (t \ 오른쪽) = e ^ {\ alpha t} $$

지수의 모양은 $ \ alpha $로 정의 할 수 있습니다. 이 기능은 3 가지 경우에 이해할 수 있습니다.

Case 1 −

$ \ alpha = 0 \ rightarrow x \ left (t \ right) = e ^ {0} = 1 $ 인 경우

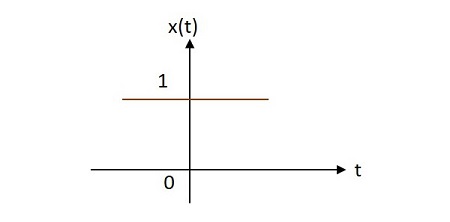
Case 2 −

$ \ alpha <0 $이면 $ x \ left (t \ right) = e ^ {\ alpha t} $ 여기서 $ \ alpha $는 음수입니다. 이 모양은decaying exponential.

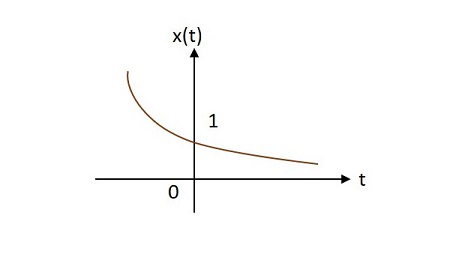
Case 3 −

$ \ alpha> 0 $이면 $ x \ left (t \ right) = e ^ {\ alpha t} $ 여기서 $ \ alpha $는 양수입니다. 이 모양은raising exponential.

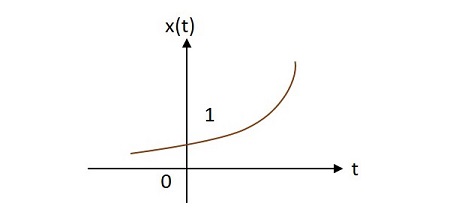
직사각형 신호

직사각형 신호는 원점에서 양의 평면과 음의 평면 모두에 직사각형 모양으로 분포 된 값을 갖습니다. 직사각형 신호의 이미지는 아래와 같습니다.

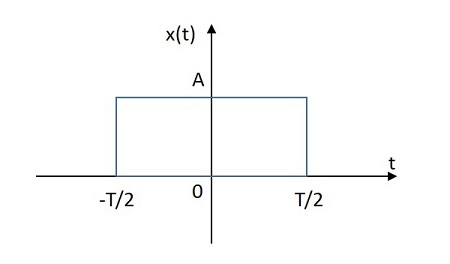
직사각형 함수는 $ x \ left (t \ right) $로 표시됩니다. 다음과 같이 정의됩니다.

$$ x \ left (t \ right) = A \ : rect \ left [\ frac {t} {T} \ right] $$

삼각 신호

직사각형 신호는 원점에서 양의 평면과 음의 평면 모두에 삼각형 모양으로 분포 된 값을 갖습니다. 삼각 신호의 이미지는 아래와 같습니다.

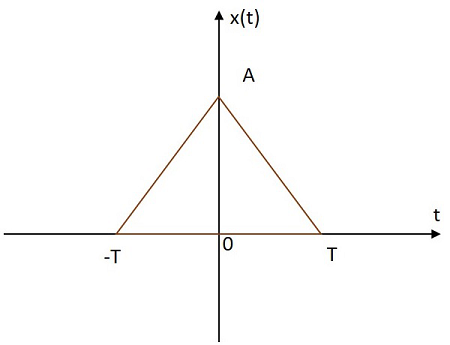
삼각 함수는 $ x \ left (t \ right) $로 표시됩니다. 다음과 같이 정의됩니다.

$$ x \ left (t \ right) = A \ left [1- \ frac {\ left | t \ 오른쪽 |} {T} \ 오른쪽] $$

정현파 신호

정현파 신호의 값은 원점에서 정현파로 변합니다. 사인파 신호의 이미지는 아래와 같습니다.

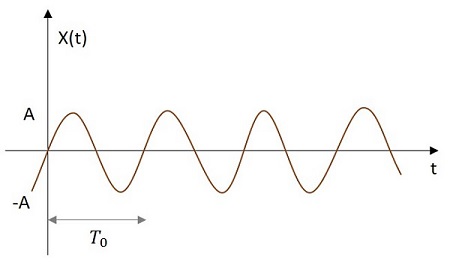
정현파 함수는 x (t)로 표시됩니다. 그것은 다음과 같이 정의됩니다-

$$ x \ left (t \ right) = A \ cos \ left (w_ {0} t \ pm \ phi \ right) $$

또는

$$ x \ left (t \ right) = 죄 \ left (w_ {0} t \ pm \ phi \ right) $$

$ T_ {0} = \ frac {2 \ pi} {w_ {0}} $

Sinc 기능

Sinc 신호는 아래 주어진 방정식에서와 같이 특정 관계에 따라 값이 달라집니다. 원점에서 최대 값을 가지며 멀어짐에 따라 계속 감소합니다. Sinc 함수 신호의 이미지는 아래와 같습니다.

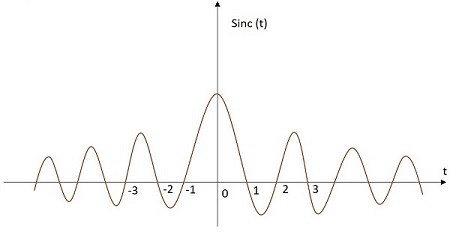
Sinc 함수는 다음과 같이 표시됩니다. sinc(t). 그것은 다음과 같이 정의됩니다-

$$ sinc \ left (t \ right) = \ frac {sin \ left (\ pi t \ right)} {\ pi t} $$

따라서 이것은 전자 및 통신 분야에서 주로 접하는 다른 신호입니다. 모든 신호를 수학 방정식으로 정의하여 신호 분석을 더 쉽게 할 수 있습니다.

각 신호는 앞에서 언급했듯이 특정 파형을 가지고 있습니다. 웨이브의 모양은 신호에 존재하는 내용을 변경할 수 있습니다. 어쨌든, 특정 회로에 대해 웨이브를 변경할지 여부는 설계 엔지니어가 결정하는 것입니다. 그러나 파도의 모양을 변경하기 위해 추가 단원에서 논의 할 기술은 거의 없습니다.