그래프 알고리즘
그래프는 객체 쌍 간의 연결을 나타내는 데 사용되는 추상 표기법입니다. 그래프는-
Vertices− 그래프에서 상호 연결된 개체를 정점이라고합니다. 정점은 다음과 같이 알려져 있습니다.nodes.
Edges − Edge는 정점을 연결하는 링크입니다.
두 가지 유형의 그래프가 있습니다.
Directed graph − 유 방향 그래프에서 모서리는 방향을 갖습니다. 즉, 모서리는 한 정점에서 다른 정점으로 이동합니다.
Undirected graph − 무 방향 그래프에서 간선에는 방향이 없습니다.
그래프 채색
그래프 색상 지정은 인접한 두 정점이 같은 색을 갖지 않도록 그래프의 정점에 색상을 할당하는 방법입니다. 일부 그래프 색상 문제는-
Vertex coloring − 인접한 두 정점이 같은 색을 공유하지 않도록 그래프의 정점을 채색하는 방법.
Edge Coloring − 인접한 두 모서리가 같은 색상을 가지지 않도록 각 모서리에 색상을 할당하는 방법입니다.
Face coloring − 평면 그래프의 각면 또는 영역에 색을 할당하여 공통 경계를 공유하는 두면이 같은 색을 갖지 않도록합니다.
색채 번호
색수는 그래프를 색칠하는 데 필요한 최소 색상 수입니다. 예를 들어, 다음 그래프의 색수는 3입니다.

그래프 채색의 개념은 시간표 작성, 모바일 무선 주파수 할당, Suduku, 레지스터 할당 및지도 채색에 적용됩니다.
그래프 채색 단계
n 차원 배열에있는 각 프로세서의 초기 값을 1로 설정합니다.
이제 특정 색상을 정점에 할당하려면 해당 색상이 인접한 정점에 이미 할당되었는지 여부를 확인합니다.
프로세서가 인접한 정점에서 동일한 색상을 감지하면 배열의 값을 0으로 설정합니다.
n 2 비교를 한 후 배열의 요소가 1이면 유효한 색상입니다.
그래프 채색을위한 의사 코드
begin
create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
status[i0,..in-1] = 1
for j varies from 0 to n-1 do
begin
for k varies from 0 to n-1 do
begin
if aj,k=1 and ij=ikthen
status[i0,..in-1] =0
end
end
ok = ΣStatus
if ok > 0, then display valid coloring exists
else
display invalid coloring
end최소 스패닝 트리
모든 모서리의 가중치 (또는 길이)의 합이 그래프 G의 다른 모든 가능한 스패닝 트리보다 작은 스패닝 트리는 minimal spanning tree 또는 minimum cost spanning나무. 다음 그림은 가중 연결 그래프를 보여줍니다.

위 그래프의 가능한 스패닝 트리는 다음과 같습니다.






위의 모든 스패닝 트리 중에서 그림 (d)는 최소 스패닝 트리입니다. 최소 비용 스패닝 트리의 개념은 출장 세일즈맨 문제, 전자 회로 설계, 효율적인 네트워크 설계, 효율적인 라우팅 알고리즘 설계에 적용됩니다.
최소 비용 스패닝 트리를 구현하기 위해 다음 두 가지 방법이 사용됩니다.
- 프림의 알고리즘
- Kruskal의 알고리즘
프림의 알고리즘
Prim의 알고리즘은 가중 된 무 방향 그래프에 대한 최소 스패닝 트리를 찾는 데 도움이되는 탐욕스러운 알고리즘입니다. 먼저 꼭지점을 선택하고 해당 꼭지점에 가장 낮은 가중치 입사를 가진 가장자리를 찾습니다.
프림 알고리즘의 단계
그래프 G의 v 1 과 같은 정점을 선택합니다 .
e 1 = v 1 v 2 및 v 1 ≠ v 2 및 e 1 이 그래프 G 에서 v 1 에 입사 하는 간선 사이에 최소 가중치를 갖도록 G의 e 1 과 같은 간선을 선택합니다 .
이제 2 단계에 따라 v 2 에서 최소 가중 에지 입사를 선택합니다 .
n–1 모서리가 선택 될 때까지 계속합니다. 여기n 정점의 수입니다.

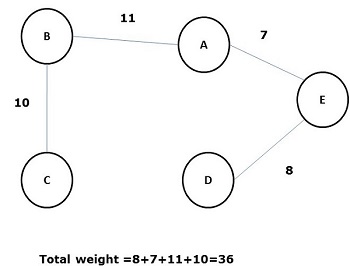
최소 스패닝 트리는-

Kruskal의 알고리즘
Kruskal의 알고리즘은 욕심 많은 알고리즘으로 연결된 가중치 그래프에 대한 최소 스패닝 트리를 찾는 데 도움이되며 각 단계에서 비용이 증가합니다. 포리스트의 두 나무를 연결하는 가능한 최소 가중치의 가장자리를 찾는 최소 스패닝 트리 알고리즘입니다.
Kruskal 알고리즘의 단계
최소 무게의 모서리를 선택하십시오. 말하자면 전자 1 그래프 G 및 E 중 하나는 루프 아니다.
e 1에 연결된 다음 최소 가중치 모서리를 선택합니다 .
n–1 모서리가 선택 될 때까지 계속합니다. 여기n 정점의 수입니다.

위 그래프의 최소 스패닝 트리는-
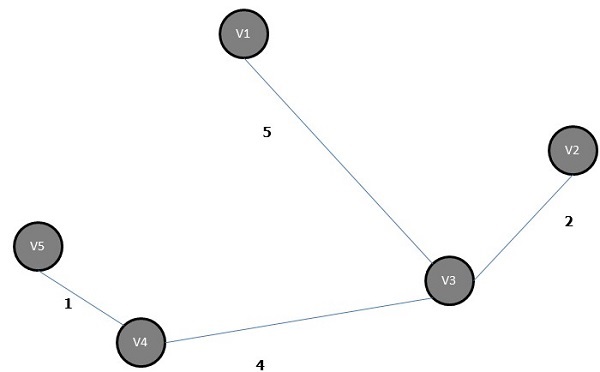
최단 경로 알고리즘
최단 경로 알고리즘은 소스 노드 (S)에서 대상 노드 (D)까지의 최소 비용 경로를 찾는 방법입니다. 여기서는 Breadth First Search Algorithm이라고도하는 Moore의 알고리즘에 대해 설명합니다.
무어의 알고리즘
소스 정점 S에 레이블을 지정하고 레이블을 지정합니다. i 및 설정 i=0.
레이블이 지정된 정점에 인접한 레이블이없는 모든 정점 찾기 i. 정점에 연결된 정점이 없으면 S, 정점 D는 S에 연결되지 않습니다. S에 연결된 정점이 있으면 레이블을 지정합니다.i+1.
D에 레이블이 지정되어 있으면 4 단계로 이동하고 그렇지 않으면 2 단계로 이동하여 i = i + 1을 늘립니다.
최단 경로의 길이를 찾은 후 중지하십시오.