진폭 변조
변조 기술 유형 중 주요 분류는 연속파 변조 및 펄스 변조입니다. 연속파 변조 기술은Amplitude Modulation 과 Angle Modulation.
연속 파는 간격없이 연속적으로 진행되며 정보를 포함하는 기저 대역 메시지 신호입니다. 이 파동은 변조되어야합니다.
표준 정의에 따르면 "반송파 신호의 진폭은 변조 신호의 순간 진폭에 따라 달라집니다." 즉, 정보를 포함하지 않는 반송파 신호의 진폭은 정보를 포함하는 각 순간에서 신호의 진폭에 따라 달라집니다. 이것은 다음 그림으로 잘 설명 될 수 있습니다.
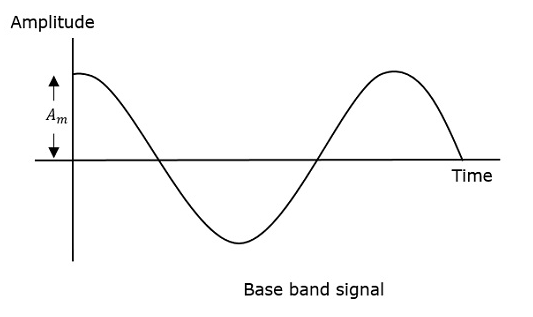
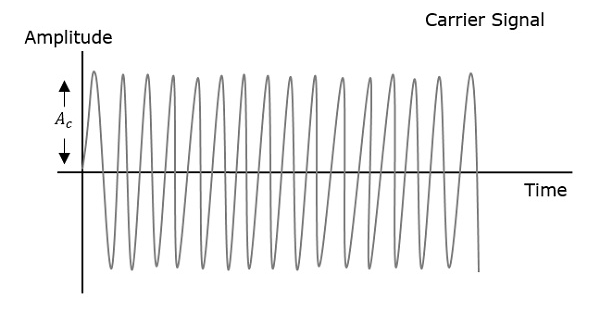
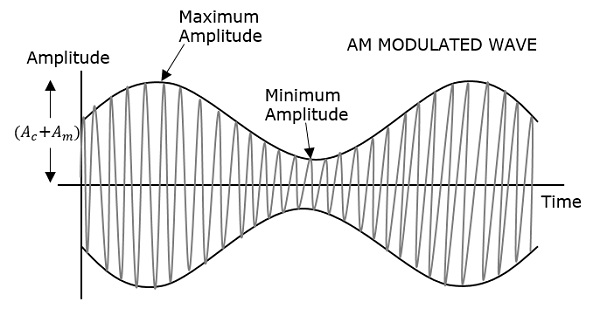
먼저 표시되는 변조 파는 메시지 신호입니다. 다음은 반송파로, 고주파 신호이며 정보를 포함하지 않습니다. 마지막 것은 결과 변조 파입니다.
반송파의 양의 피크와 음의 피크가 가상의 선과 상호 연결되어 있음을 알 수 있습니다. 이 라인은 변조 신호의 정확한 모양을 재현하는 데 도움이됩니다. 반송파의이 가상 선을Envelope. 메시지 신호와 동일합니다.
수학적 표현
다음은 이러한 파동에 대한 수학적 표현입니다.
파동의 시간 영역 표현
변조 신호를-
$$ m (t) = A_mcos (2 \ pi f_mt) $$
반송파 신호를-
$$ c (t) = A_ccos (2 \ pi f_ct) $$
어디 Am = 변조 신호의 최대 진폭
Ac = 반송파 신호의 최대 진폭
진폭 변조 파의 표준 형태는 다음과 같이 정의됩니다.
$$ S (t) = A_c [1 + K_am (t)] cos (2 \ pi f_ct) $$
$$ S (t) = A_c [1+ \ mu cos (2 \ pi f_mt)] cos (2 \ pi f_ct) $$
$$ 어디서, \ mu = K_aA_m $$
변조 지수
반송파는 변조 된 후 변조 된 레벨이 계산되면 이러한 시도를 다음과 같이 호출합니다. Modulation Index 또는 Modulation Depth. 반송파가 겪는 변조 수준을 나타냅니다.
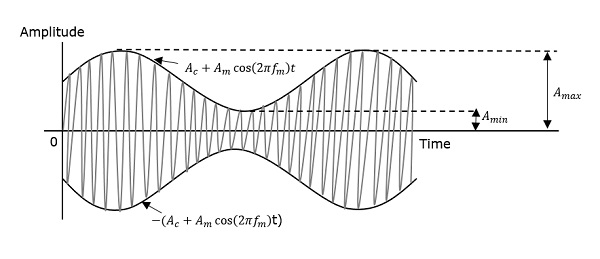
변조 된 파형의 포락선의 최대 값과 최소값은 각각 A max 및 A min으로 표시 됩니다.
변조 지수에 대한 방정식을 개발해 보겠습니다.
$$ A_ {최대} = A_c (1+ \ mu) $$
A max 에서 cos θ의 값은 1 이기 때문에
$$ A_ {분} = A_c (1- \ mu) $$
A min 에서 cos θ 값은 -1 이기 때문에
$$ \ frac {A_ {최대}} {A_ {min}} = \ frac {1+ \ mu} {1- \ mu} $$
$$ A_ {최대}-\ mu A_ {최대} = A_ {min} + \ mu A_ {min} $$
$$-\ mu (A_ {max} + A_ {min}) = A_ {min} -A_ {max} $$
$$ \ mu = \ frac {A_ {max} -A_ {min}} {A_ {max} + A_ {min}} $$
따라서 변조 지수에 대한 방정식이 얻어집니다. µ변조 인덱스 또는 변조 깊이를 나타냅니다. 이것은 종종 다음과 같이 백분율로 표시됩니다.Percentage Modulation. 백분율로 표시되는 변조의 범위이며 다음으로 표시됩니다.m.
완벽한 변조를 위해서는 변조 지수 값이 1이어야하며, 이는 변조 깊이가 100 % 여야 함을 의미합니다.
예를 들어,이 값이 1 미만인 경우, 즉 변조 지수가 0.5이면 변조 된 출력은 다음 그림과 같습니다. 이를 Under-modulation이라고합니다. 이러한 파동을under-modulated wave.
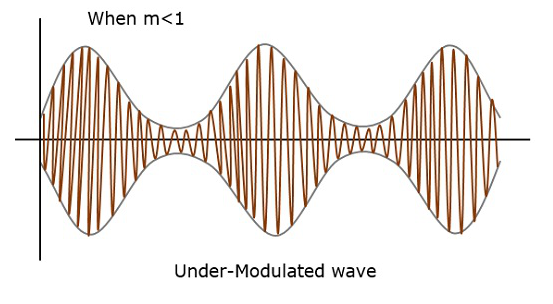
변조 지수의 값이 1보다 크면, 즉 1.5 정도이면 파동은 over-modulated wave. 다음 그림과 같습니다.

변조 지수의 값이 증가함에 따라 반송파는 180 ° 위상 반전을 경험하여 추가적인 측 파대가 발생하여 파동이 왜곡됩니다. 이러한과 변조 된 파동은 제거 할 수없는 간섭을 유발합니다.
진폭 변조의 대역폭
대역폭은 신호의 최저 주파수와 최고 주파수 사이의 차이입니다.
진폭 변조 파의 경우 대역폭은 다음과 같이 지정됩니다.
$$ BW = f_ {USB} -f_ {LSB} $$
$$ (f_c + f_m)-(f_c-f_m) $$
$$ = 2f_m = 2W $$
어디 W 메시지 대역폭입니다.
따라서 진폭 변조 파에 필요한 대역폭은 변조 신호 주파수의 두 배라는 것을 알게되었습니다.