시간축 생성기 개요
펄스 회로의 기본 사항을 논의한 후 이제 생성하고 처리하는 다양한 회로를 살펴 보겠습니다. Saw tooth waves. 톱니파는 시간이 지남에 따라 선형 적으로 증가하고 갑작스럽게 감소합니다. 이것은 또한Time base signal. 실제로 이것은 시간축 생성기의 이상적인 출력입니다.
시간축 생성기 란 무엇입니까?
생성하는 전자 발전기 high frequency saw tooth waves 로 불릴 수 있습니다 Time Base Generator. 또한 출력 전압 또는 전류 파형을 생성하는 전자 회로로 이해 될 수 있습니다.varies linearly with time. 시간축 생성기의 수평 속도는 일정해야합니다.
오실로스코프에서 시간에 따른 신호의 변화를 표시하려면 시간에 따라 선형 적으로 변화하는 전압을 편향 판에 적용해야합니다. 이것은 신호가 화면을 가로 질러 수평으로 빔을 스윕하도록합니다. 따라서 전압은Sweep Voltage. 타임베이스 생성기는 다음과 같이 호출됩니다.Sweep Circuits.
타임베이스 신호의 특징
CRO 또는 픽처 튜브에서 시간축 파형을 생성하려면 편향 전압이 시간에 따라 선형 적으로 증가합니다. 일반적으로 빔이 화면에서 선형으로 편향되어 시작점으로 돌아 오는 경우 타임베이스 생성기가 사용됩니다. 이것은 과정에서 발생합니다Scanning. 음극선 관과 그림 관도 같은 원리로 작동합니다. 빔은 화면에서 한쪽에서 다른쪽으로 (일반적으로 왼쪽에서 오른쪽으로) 편향되고 동일한 지점으로 돌아옵니다.
이 현상은 Trace 과 Retrace. 화면에서 왼쪽에서 오른쪽으로 빔의 편향을 다음과 같이 부릅니다.Trace, 빔의 오른쪽에서 왼쪽으로의 복귀는 Retrace 또는 Fly back. 일반적으로이 귀선은 보이지 않습니다. 이 프로세스는 사용 된 RC 구성 요소의 도움으로 편향 기간을 설정하는 톱니파 생성기의 도움으로 수행됩니다.
톱니파의 부분을 이해하려고 노력합시다.

위의 신호에서 출력이 선형 적으로 증가하는 시간을 다음과 같이 호출합니다. Sweep Time (TS) 신호가 초기 값으로 돌아가는 데 걸리는 시간은 다음과 같이 호출됩니다. Restoration Time 또는 Fly back Time 또는 Retrace Time (Tr). 이 두 기간은 함께 타임베이스 신호의 한 사이클의 기간을 형성합니다.
실제로 우리가 얻는이 스위프 전압 파형은 스위프 회로의 실제 출력 인 반면 이상적인 출력은 위 그림에 표시된 톱니 파형이어야합니다.
시간축 생성기의 유형
타임베이스 생성기에는 두 가지 유형이 있습니다. 그들은-
Voltage Time Base Generators − 시간에 따라 선형 적으로 변화하는 출력 전압 파형을 제공하는 타임베이스 생성기를 전압 타임베이스 생성기라고합니다.
Current Time Base Generator − 시간에 따라 선형 적으로 변화하는 출력 전류 파형을 제공하는 시간 기반 생성기를 현재 시간 기반 생성기라고합니다.
응용
Time Base Generator는 CRO, 텔레비전, RADAR 디스플레이, 정밀 시간 측정 시스템 및 시간 변조에 사용됩니다.
스위프 신호의 오류
스위프 신호를 생성 한 후 전송할 시간입니다. 전송 된 신호는 선형성에서 벗어날 수 있습니다. 발생한 오류를 이해하고 수정하려면 발생하는 일반적인 오류에 대한 지식이 있어야합니다.
선형성 편차는 세 가지 방식으로 표현됩니다. 그들은-
- 슬로프 또는 스위프 속도 오류
- 변위 오류
- 전송 오류
이에 대해 자세히 논의하겠습니다.
슬로프 또는 스위프 속도 오류 (e s )
스위프 전압은 시간에 따라 선형 적으로 증가해야합니다. 시간에 따른 스위프 전압의 변화율은 일정해야합니다. 이 선형성 편차는 다음과 같이 정의됩니다.Slope Speed Error 또는 Sweep Speed Error.
경사 또는 스위프 속도 eror 전자 S = $ \ FRAC {\에서 : 경사 \ 차이 \ \에서 다음 \ 시작 \와 \ 단부 \ : \의 : 스위프} \ {초기 : 값 \의 \ : 기울기} $
$$ = \ frac {\ left (\ frac {\ mathrm {d} V_0} {\ mathrm {d} t} \ right) _ {t = 0}-\ left (\ frac {\ mathrm {d} V_0} {\ mathrm {d} t} \ right) _ {t = T_s}} {\ left (\ frac {\ mathrm {d} V_0} {\ mathrm {d} t} \ right) _ {t = 0}} $$
변위 오류 (e d )
선형성의 중요한 기준은 실제 스위프 전압과 실제 스위프의 시작점과 끝점을 통과하는 선형 스위프 간의 최대 차이입니다.
이것은 다음 그림에서 이해할 수 있습니다.
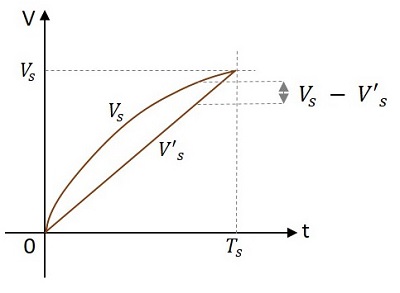
변위 오류 ed 다음과 같이 정의됩니다.
e d = $ \ frac {(실제 \ : 속도) \ thicksim (선형 \ : 스윕 \ : that \ : 패스 \ : 시작 \ : 및 \ : 끝 \ : of \ : 실제 \ : 스윕)} {amplitude \ : of \ : 스윕 \ : at \ : \ : 종료 \ : of \ : 스윕 \ : 시간} $
$$ = \ : \ frac {(V_s-V′_s) _ {max}} {V_s} $$
어디 V s는 실제 스윕과 V ' 의이 선형 스윕이다.
전송 오류 (e t )
스위프 신호가 하이 패스 회로를 통과하면 아래와 같이 출력이 입력에서 벗어납니다.
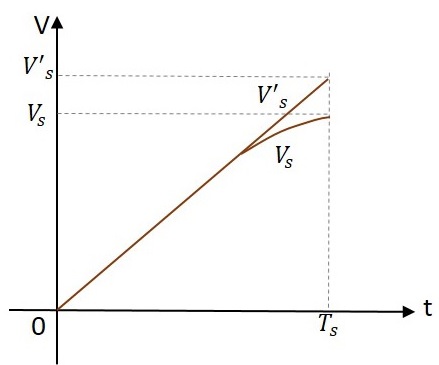
이 편차는 전송 오류로 표현됩니다.
전송 오류 = $ \ frac {(input) \ : \ thicksim \ :( output)} {input \ : at \ : the \ : end \ : of \ : the \ : sweep} $
$$ e_t = \ frac {V′_s − V} {V′_s} $$
여기서 V ' S는 입력이고, V S는 t = T에서 스윕 즉 끝의 출력 들 .
선형성 편차가 매우 작고 스위프 전압이 t의 선형 및 2 차 항의 합으로 근사 될 수있는 경우 위의 세 오류는 다음과 관련됩니다.
$$ e_d = \ frac {e_s} {8} = \ frac {e_t} {4} $$
$$ e_s = 2e_t = 8e_d $$
스위프 속도 오류는 변위 오류보다 더 지배적입니다.