계산 그래프
역전 파는 계산 그래프를 사용하여 Tensorflow, Torch, Theano 등과 같은 딥 러닝 프레임 워크에서 구현됩니다. 더 중요한 것은 계산 그래프에서 역 전파를 이해하면 여러 다른 알고리즘과 시간을 통한 역 전파 및 공유 가중치와 역전 파와 같은 변형을 결합합니다. 모든 것이 계산 그래프로 변환되면 여전히 동일한 알고리즘입니다. 계산 그래프에서 역전 파일뿐입니다.
계산 그래프 란?
계산 그래프는 노드가 수학적 연산에 해당하는 방향 그래프로 정의됩니다. 계산 그래프는 수학적 표현을 표현하고 평가하는 방법입니다.
예를 들어, 다음은 간단한 수학 방정식입니다.
$$ p = x + y $$
위 방정식의 계산 그래프를 다음과 같이 그릴 수 있습니다.
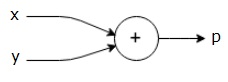
위의 계산 그래프에는 두 개의 입력 변수 x와 y와 하나의 출력 q가있는 더하기 노드 ( "+"기호가있는 노드)가 있습니다.
약간 더 복잡한 또 다른 예를 들어 보겠습니다. 다음 방정식이 있습니다.
$$ g = \ 왼쪽 (x + y \ 오른쪽) \ ast z $$
위의 방정식은 다음 계산 그래프로 표시됩니다.
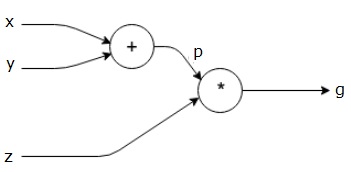
계산 그래프와 역 전파
계산 그래프와 역전 파는 모두 신경망 훈련을위한 딥 러닝의 중요한 핵심 개념입니다.
포워드 패스
정방향 통과는 계산 그래프로 표현 된 수학적 표현의 값을 평가하는 절차입니다. 정방향 전달을 수행한다는 것은 출력이있는 왼쪽 (입력)에서 오른쪽으로 정방향으로 변수의 값을 전달한다는 것을 의미합니다.
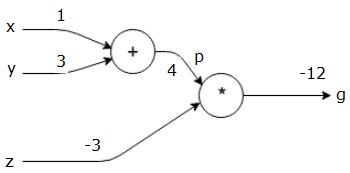
모든 입력에 값을 부여하여 예를 고려해 보겠습니다. 모든 입력에 다음 값이 제공된다고 가정합니다.
$$ x = 1, y = 3, z = −3 $$
이러한 값을 입력에 제공하면 순방향 전달을 수행하고 각 노드의 출력에 대해 다음 값을 얻을 수 있습니다.
먼저 x = 1 및 y = 3의 값을 사용하여 p = 4를 얻습니다.

그런 다음 p = 4 및 z = -3을 사용하여 g = -12를 얻습니다. 우리는 왼쪽에서 오른쪽으로 앞으로 이동합니다.
역방향 패스의 목적
역방향 패스에서 우리의 의도는 최종 출력과 관련하여 각 입력에 대한 기울기를 계산하는 것입니다. 이러한 기울기는 기울기 하강 법을 사용하여 신경망을 훈련하는 데 필수적입니다.
예를 들어 다음과 같은 그라디언트가 필요합니다.
원하는 그라디언트
$$ \ frac {\ partial x} {\ partial f}, \ frac {\ partial y} {\ partial f}, \ frac {\ partial z} {\ partial f} $$
역방향 전달 (역 전파)
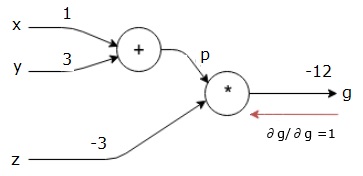
최종 출력 (그 자체!)에 대한 최종 출력의 미분을 찾아서 역방향 패스를 시작합니다. 따라서 ID 파생이 발생하고 값은 1과 같습니다.
$$ \ frac {\ partial g} {\ partial g} = 1 $$
우리의 계산 그래프는 이제 아래와 같이 보입니다.
다음으로 "*"연산을 통해 역방향 패스를 수행합니다. p와 z에서 기울기를 계산합니다. g = p * z이므로-
$$ \ frac {\ partial g} {\ partial z} = p $$
$$ \ frac {\ partial g} {\ partial p} = z $$
우리는 이미 정방향 패스에서 z와 p의 값을 알고 있습니다. 따라서 우리는-
$$ \ frac {\ partial g} {\ partial z} = p = 4 $$
과
$$ \ frac {\ partial g} {\ partial p} = z = -3 $$
우리는 x와 y에서 기울기를 계산하고 싶습니다-
$$ \ frac {\ partial g} {\ partial x}, \ frac {\ partial g} {\ partial y} $$
그러나 우리는 이것을 효율적으로 수행하기를 원합니다 (이 그래프에서 x와 g는 두 홉 밖에 떨어져 있지 않지만 실제로 서로 멀리 떨어져 있다고 상상해보십시오). 이러한 값을 효율적으로 계산하기 위해 미분의 체인 규칙을 사용합니다. 체인 규칙에서 우리는-
$$ \ frac {\ partial g} {\ partial x} = \ frac {\ partial g} {\ partial p} \ ast \ frac {\ partial p} {\ partial x} $$
$$ \ frac {\ partial g} {\ partial y} = \ frac {\ partial g} {\ partial p} \ ast \ frac {\ partial p} {\ partial y} $$
그러나 p는 x와 y에 직접 의존하기 때문에 dg / dp = -3, dp / dx 및 dp / dy가 쉽다는 것을 이미 알고 있습니다. 우리는-
$$ p = x + y \ Rightarrow \ frac {\ partial x} {\ partial p} = 1, \ frac {\ partial y} {\ partial p} = 1 $$
따라서 우리는-
$$ \ frac {\ partial g} {\ partial f} = \ frac {\ partial g} {\ partial p} \ ast \ frac {\ partial p} {\ partial x} = \ left (-3 \ right) .1 = -3 $$
또한 입력 y-
$$ \ frac {\ partial g} {\ partial y} = \ frac {\ partial g} {\ partial p} \ ast \ frac {\ partial p} {\ partial y} = \ left (-3 \ right) .1 = -3 $$
이 작업을 거꾸로 수행하는 주된 이유는 x에서 기울기를 계산해야 할 때 이미 계산 된 값과 dq / dx (동일한 노드의 입력에 대한 노드 출력의 미분) 만 사용했기 때문입니다. 우리는 지역 정보를 사용하여 글로벌 가치를 계산했습니다.
신경망 훈련 단계
신경망을 훈련하려면 다음 단계를 따르십시오.
데이터 세트의 데이터 포인트 x에 대해 x를 입력으로 전달하고 비용 c를 출력으로 계산합니다.
c에서 시작하여 역방향 패스를 수행하고 그래프의 모든 노드에 대한 기울기를 계산합니다. 여기에는 신경망 가중치를 나타내는 노드가 포함됩니다.
그런 다음 W = W-학습률 * 기울기를 수행하여 가중치를 업데이트합니다.
중지 기준이 충족 될 때까지이 프로세스를 반복합니다.