위성 통신-케플러의 법칙

우리는 위성이 지구를 중심으로 회전한다는 것을 알고 있습니다. 지구가 태양을 중심으로 회전하는 것과 비슷합니다. 따라서 지구에 적용되는 원리와 태양 주위의 움직임은 위성과 지구 주위의 움직임에도 적용됩니다.

많은 과학자들이 초기부터 다양한 유형의 이론을 제시했습니다. 하지만Johannes Kepler (1571-1630)은 지구 주위를 움직이는 위성의 원리를 설명하는 데 가장 인정받는 과학자 중 한 명이었습니다.

케플러는 전체 위성 통신 이론과 관측을 바꾸는 세 가지 법칙을 공식화했습니다. 이것들은 널리 알려져 있습니다Kepler’s laws. 이것은 공간을 통한 움직임을 시각화하는 데 도움이됩니다.

케플러의 첫 번째 법칙

케플러의 첫 번째 법칙은 주 (지구) 주변의 위성이 따라가는 경로는 ellipse. 이 타원에는 아래 그림과 같이 두 개의 초점 (초점) F1과 F2가 있습니다. 지구의 질량 중심은 항상 타원의 두 초점 중 하나에 표시됩니다.

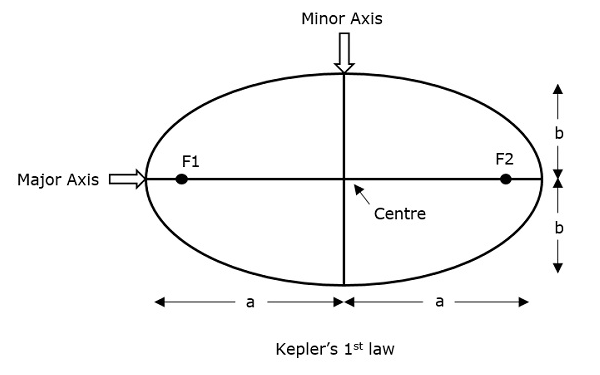
객체의 중심에서 타원 경로의 점까지의 거리를 고려하면 중심에서 타원의 가장 먼 점을 다음과 같이 호출합니다. apogee 그리고 중심에서 타원의 가장 짧은 점은 perigee.

Eccentricity "e" 이 시스템의 다음과 같이 쓸 수 있습니다-

$$e = \frac{\sqrt{a^2 - b^2}}{a}$$

어디, a & b 타원의 반 장축 및 반 단축의 길이입니다.

에 대한 elliptical path, 편심 (e)의 값은 항상 0과 1 사이에 있습니다. 즉 $0$ < $e$ < $1$, a가 b보다 크기 때문입니다. 편심 (e) 값이 0이면 경로가 더 이상 타원형이 아니라 원형으로 변환된다고 가정합니다.

케플러의 두 번째 법칙은 동일한 시간 간격에 대해 area위성에 의해 커버되는 것은 지구의 질량 중심에 대해 동일합니다. 이것은 다음 그림을 살펴보면 이해할 수 있습니다.

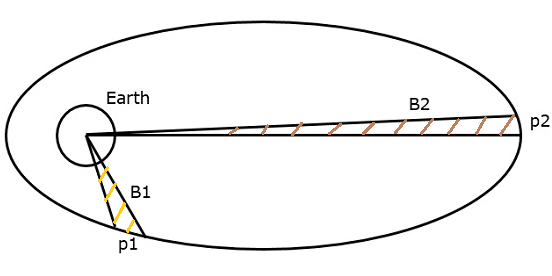
위성이 동일한 시간 간격으로 p1 및 p2 거리를 커버한다고 가정합니다. 그러면이 두 인스턴스에서 위성이 커버하는 영역 B1과 B2는 동일합니다.

케플러의 세 번째 법칙에 따르면 타원 궤도의 주기적 시간의 제곱은 반장 축 길이의 큐브에 비례합니다. Mathematically, 다음과 같이 쓸 수 있습니다-

$$T^2\:\alpha\:a^3$$

$$=> T^2=\left(\frac{4\pi ^2}{\mu }\right) a^3$$

어디, $\frac{4\pi^2}{\mu}$ 비례 상수입니다.

$\mu$케플러 상수이고 그 값은 3.986005 x 10 ¹⁴ m ³ / sec ^{2와 같습니다.}

$$1 = \left(\frac{2\pi}{T}\right)^2\left(\frac{a^2}{\mu}\right)$$

$$1 = n^2\left(\frac{a^3}{\mu}\right)$$

$$=> a^3 = \frac{\mu}{n^2}$$

어디, ‘n’ 초당 라디안 단위의 위성 평균 움직임입니다.

Note− 위성은 지구 주위를 공전 할 때 지구에서 당기는 힘, 즉 중력을받습니다. 마찬가지로, 그것은 태양과 달에서 또 다른 당기는 힘을 경험합니다. 따라서 위성은 궤도를 유지하기 위해이 두 힘의 균형을 맞춰야합니다.