위성 통신-궤도 역학
우리는 지구를 도는 위성의 경로가 orbit. 이 경로는 수학적 표기법으로 나타낼 수 있습니다. 궤도 역학은 궤도에 존재하는 위성의 움직임을 연구하는 것입니다. 따라서 우리는 궤도 운동에 대한 지식으로 우주 작업을 쉽게 이해할 수 있습니다.
궤도 요소
궤도 요소는 매개 변수로, 위성의 궤도 운동을 설명하는 데 도움이됩니다. 다음은orbital elements.
- 준 장축
- Eccentricity
- 평균 이상
- 근지점의 주장
- Inclination
- 오름차순 노드의 적경
위의 6 개의 궤도 요소는 지구 위성의 궤도를 정의합니다. 따라서 궤도 요소의 값에 따라 하나의 위성을 다른 위성과 구별하기 쉽습니다.
준 장축
길이 Semi-major axis (a)위성의 궤도 크기를 정의합니다. 장축의 절반입니다. 이것은 중심에서 초점을 통해 타원의 가장자리까지 이어집니다. 따라서 그것은 궤도에서 가장 먼 두 지점에서 궤도의 반경입니다.
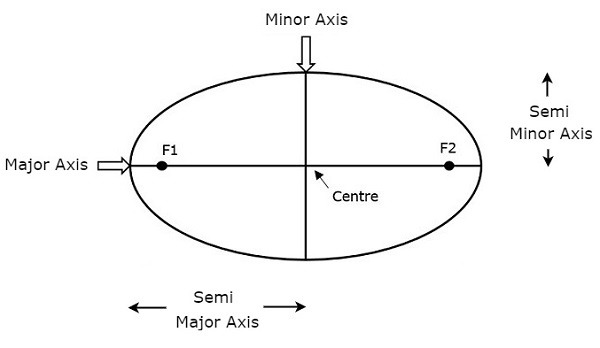
준 장축과 준 단축이 위 그림에 표시되어 있습니다. 세미 길이major axis (a) 위성의 궤도 크기뿐만 아니라 회전 시간도 결정합니다.
원형 궤도가 특별한 경우로 간주되면 반장 축의 길이는 다음과 같습니다. radius 그 원형 궤도의.
이심률
의 가치 Eccentricity (e)위성 궤도의 모양을 수정합니다. 이 매개 변수는 완벽한 원에서 궤도 모양의 편차를 나타냅니다.
타원 궤도의 준 장축과 준 단축의 길이가 a & b 인 경우에 대한 수학 식 eccentricity (e) 될거야
$$ e = \ frac {\ sqrt {a ^ 2-b ^ 2}} {a} $$
원형 궤도의 편심 값은 다음과 같습니다. zero, a와 b가 모두 같기 때문입니다. 반면 타원 궤도의 편심 값은 0과 1 사이에 있습니다.
다음과 같은 figure 서로 다른 편심 (e) 값에 대한 다양한 위성 궤도를 보여줍니다.
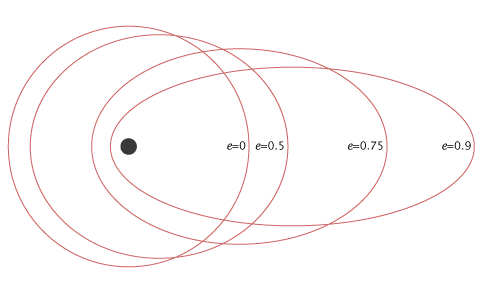
위 그림에서 편심 (e) 값 0에 해당하는 위성 궤도는 원형 궤도입니다. 그리고 나머지 3 개의 위성 궤도는 편심 (e) 값 0.5, 0.75 및 0.9에 해당하는 타원형입니다.
평균 이상
위성의 경우 지구에서 가장 가까운 지점을 Perigee라고합니다. Mean anomaly (M)은 근지를 기준으로 위성의 각도 위치 평균값을 제공합니다.
궤도가 원형이면 평균 이상은 궤도에서 위성의 각도 위치를 제공합니다. 그러나 궤도가 타원형이라면 정확한 위치를 계산하는 것이 매우 어렵습니다. 이때 평균 이상은 중간 단계로 사용됩니다.
Perigee의 주장
위성 궤도는 적도면을 두 지점에서 자릅니다. 첫 번째 포인트는descending node, 위성이 북반구에서 남반구로 이동하는 곳. 두 번째 포인트는ascending node, 위성이 남반구에서 북반구로 이동하는 곳.
Argument of perigee (ω)오름차순 노드와 근점 사이의 각도입니다. 근지점과 오름차순 노드가 같은 지점에있는 경우 근지점의 인수는 0 도가됩니다.
근지점의 인수는 위성 운동 방향으로 지구 중심의 궤도면에서 측정됩니다.
기울기
궤도면과 지구의 적도면 사이의 각도는 다음과 같이 알려져 있습니다. inclination (i). 방향은 동쪽에서 북쪽으로 오름차순 노드에서 측정됩니다. 따라서 기울기는 지구의 적도를 기준으로 고려하여 궤도의 방향을 정의합니다.

경사각에 따라 네 가지 유형의 궤도가 있습니다.
Equatorial orbit − 경사각은 0도 또는 180 도입니다.
Polar orbit − 경사각은 90 도입니다.
Prograde orbit − 경사각은 0도에서 90도 사이입니다.
Retrograde orbit − 경사각은 90도에서 180도 사이입니다.
오름차순 노드의 적경
우리는 알고 있습니다 ascending node 위성이 남반구에서 북반구로 이동하면서 적도면을 가로 지르는 지점입니다.
오름차순 노드의 적경 (Ω)양자리 선과 적도면에서 동쪽 방향을 향한 상승 노드 사이의 각도입니다. 양자리는 춘분과 춘분이라고도합니다.
위성 ground track궤도 바로 아래에있는 지구 표면의 경로입니다. 위성의 지상 트랙은 궤도 요소의 값에 따라 다양한 형태를 취할 수 있습니다.
궤도 방정식
이 섹션에서는 궤도 운동과 관련된 방정식에 대해 논의하겠습니다.
위성에 작용하는 힘
위성은 지구 주위를 공전 할 때 지구의 중력으로 인해 지구에서 당기는 힘을받습니다. 이 힘은Centripetal force(F 1 )이 힘은 위성을 향하게하기 때문입니다.
수학적으로 Centripetal force(F 1 ) 지구로 인해 위성에 작용하는 것은 다음과 같이 쓸 수 있습니다.
$$ F_ {1} = \ frac {GMm} {R ^ 2} $$
어디,
G만유 중력 상수이고 6.673 x 10 -11 N ∙ m 2 / kg 2 입니다.
M지구의 질량이며 5.98 x 10 24 Kg입니다.
m 위성의 질량입니다.
R 위성에서 지구 중심까지의 거리입니다.
위성은 지구 주위를 공전 할 때 중력으로 인해 태양과 달에서 당기는 힘을받습니다. 이 힘은Centrifugal force(F 2 )이 힘은 위성을 지구에서 멀어지게하기 때문입니다.
수학적으로 Centrifugal force(F 2 ) 위성에서 작동하는 것은 다음과 같이 쓸 수 있습니다.
$$ F_ {2} = \ frac {mv ^ 2} {R} $$
어디, v 위성의 궤도 속도입니다.
궤도 속도
위성의 궤도 속도는 위성이 지구를 중심으로 회전하는 속도입니다. 구심력과 원심력이 모두 존재할 때 위성은 궤도에서 벗어나지 않고 해당 궤도에서 특정 속도로 이동합니다.balance 서로.
그래서, equate구심력 (F 1 ) 및 원심력 (F 2 ).
$$ \ frac {GMm} {R ^ 2} = \ frac {mv ^ 2} {R} $$
$$ => \ frac {GM} {R} = v ^ 2 $$
$$ => v = \ sqrt {\ frac {GM} {R}} $$
따라서 orbital velocity 위성의
$$ v = \ sqrt {\ frac {GM} {R}} $$
어디,
G중력 상수이고 6.673 x 10 -11 N ∙ m 2 / kg 2 입니다.
M지구의 질량이며 5.98 x 10 24 Kg입니다.
R 위성에서 지구 중심까지의 거리입니다.
그래서, 궤도 속도는 주로 depends G & M은 상수이기 때문에 위성에서 지구 중심까지의 거리 (R).