Scikit Learn-퀵 가이드

이 장에서는 Scikit-Learn 또는 Sklearn이 무엇인지, Scikit-Learn의 기원과 Scikit-Learn의 개발 및 유지 관리를 담당하는 커뮤니티 및 기여자, 전제 조건, 설치 및 기능과 같은 기타 관련 주제를 이해합니다.

Scikit-Learn (Sklearn)이란?

Scikit-learn (Sklearn)은 Python의 기계 학습을위한 가장 유용하고 강력한 라이브러리입니다. Python의 일관성 인터페이스를 통해 분류, 회귀, 클러스터링 및 차원 감소를 포함한 기계 학습 및 통계 모델링을위한 효율적인 도구를 제공합니다. 주로 Python으로 작성된이 라이브러리는NumPy, SciPy 과 Matplotlib.

Scikit-Learn의 기원

원래는 scikits.learn 2007 년 Google 여름 코드 프로젝트로 David Cournapeau에 의해 처음 개발되었습니다. 나중에 2010 년 FIRCA (French Institute for Research in Computer Science and Automation)의 Fabian Pedregosa, Gael Varoquaux, Alexandre Gramfort 및 Vincent Michel이 이 프로젝트는 2010 년 2 월 1 일에 첫 번째 공개 릴리스 (v0.1 베타)를 만들었습니다.

버전 기록을 살펴 보겠습니다.

• 2019 년 5 월 : scikit-learn 0.21.0

• 2019 년 3 월 : scikit-learn 0.20.3

• 2018 년 12 월 : scikit-learn 0.20.2

• 2018 년 11 월 : scikit-learn 0.20.1

• 2018 년 9 월 : scikit-learn 0.20.0

• 2018 년 7 월 : scikit-learn 0.19.2

• 2017 년 7 월 : scikit-learn 0.19.0

• 2016 년 9 월. scikit-learn 0.18.0

• 2015 년 11 월. scikit-learn 0.17.0

• 2015 년 3 월. scikit-learn 0.16.0

• 2014 년 7 월. scikit-learn 0.15.0

• 2013 년 8 월. scikit-learn 0.14

커뮤니티 및 기여자

Scikit-learn은 커뮤니티의 노력이며 누구나 참여할 수 있습니다. 이 프로젝트는https://github.com/scikit-learn/scikit-learn. 다음 사람들은 현재 Sklearn의 개발 및 유지 관리에 핵심 기여자입니다.

• Joris Van den Bossche (데이터 과학자)

• Thomas J Fan (소프트웨어 개발자)

• Alexandre Gramfort (기계 학습 연구원)

• Olivier Grisel (기계 학습 전문가)

• Nicolas Hug (부 연구 과학자)

• Andreas Mueller (기계 학습 과학자)

• 진한 민 (소프트웨어 엔지니어)

• Adrin Jalali (오픈 소스 개발자)

• Nelle Varoquaux (데이터 과학 연구원)

• Roman Yurchak (데이터 과학자)

Booking.com, JP Morgan, Evernote, Inria, AWeber, Spotify 등과 같은 다양한 조직에서 Sklearn을 사용하고 있습니다.

전제 조건

scikit-learn 최신 릴리스를 사용하기 전에 다음이 필요합니다.

• Python (> = 3.5)

• NumPy (> = 1.11.0)

• Scipy (> = 0.17.0) li

• Joblib (> = 0.11)

• Sklearn 플로팅 기능에는 Matplotlib (> = 1.5.1)이 필요합니다.

• 데이터 구조 및 분석을 사용하는 일부 scikit-learn 예제에는 Pandas (> = 0.18.0)가 필요합니다.

설치

NumPy와 Scipy를 이미 설치했다면 다음은 scikit-learn을 설치하는 가장 쉬운 두 가지 방법입니다.

pip 사용

다음 명령을 사용하여 pip를 통해 scikit-learn을 설치할 수 있습니다.

pip install -U scikit-learn

conda 사용

다음 명령은 conda를 통해 scikit-learn을 설치하는 데 사용할 수 있습니다-

conda install scikit-learn

반면에 NumPy 및 Scipy가 Python 워크 스테이션에 아직 설치되지 않은 경우 다음 중 하나를 사용하여 설치할 수 있습니다. pip 또는 conda.

scikit-learn을 사용하는 또 다른 옵션은 다음과 같은 Python 배포를 사용하는 것입니다. Canopy 과 Anaconda 둘 다 최신 버전의 scikit-learn을 제공하기 때문입니다.

풍모

Scikit-learn 라이브러리는 데이터로드, 조작 및 요약에 중점을 두는 대신 데이터 모델링에 중점을 둡니다. Sklearn에서 제공하는 가장 인기있는 모델 그룹은 다음과 같습니다.

Supervised Learning algorithms − Linear Regression, SVM (Support Vector Machine), Decision Tree 등과 같은 거의 모든 인기있는지도 학습 알고리즘이 scikit-learn의 일부입니다.

Unsupervised Learning algorithms -한편, 클러스터링, 요인 분석, PCA (주성분 분석)에서 비지도 신경망에 이르기까지 널리 사용되는 비지도 학습 알고리즘을 모두 갖추고 있습니다.

Clustering −이 모델은 레이블이없는 데이터를 그룹화하는 데 사용됩니다.

Cross Validation − 보이지 않는 데이터에 대한 감독 모델의 정확성을 확인하는 데 사용됩니다.

Dimensionality Reduction − 요약, 시각화 및 기능 선택에 추가로 사용할 수있는 데이터의 속성 수를 줄이는 데 사용됩니다.

Ensemble methods − 이름에서 알 수 있듯이 여러 감독 모델의 예측을 결합하는 데 사용됩니다.

Feature extraction − 데이터에서 특징을 추출하여 이미지 및 텍스트 데이터의 속성을 정의하는 데 사용됩니다.

Feature selection −지도 모델 생성에 유용한 속성을 식별하는 데 사용됩니다.

Open Source − 오픈 소스 라이브러리이며 BSD 라이선스에 따라 상업적으로도 사용할 수 있습니다.

이 장에서는 Sklearn과 관련된 모델링 프로세스를 다룹니다. 이에 대해 자세히 이해하고 데이터 세트로드부터 시작하겠습니다.

데이터 세트로드

데이터 모음을 데이터 세트라고합니다. 그것은 다음 두 가지 구성 요소를 가지고 있습니다-

Features− 데이터의 변수를 특성이라고합니다. 예측 자, 입력 또는 속성이라고도합니다.

• Feature matrix − 하나 이상의 기능이있는 경우 기능 모음입니다.

• Feature Names − 기능의 모든 이름의 목록입니다.

Response− 기본적으로 특성 변수에 따라 달라지는 출력 변수입니다. 대상, 레이블 또는 출력이라고도합니다.

• Response Vector− 응답 열을 나타내는 데 사용됩니다. 일반적으로 응답 열은 하나만 있습니다.

• Target Names − 응답 벡터가 취할 수있는 값을 나타냅니다.

Scikit-learn에는 다음과 같은 예제 데이터 세트가 거의 없습니다. iris 과 digits 분류 및 Boston house prices 회귀를 위해.

예

다음은로드하는 예입니다. iris 데이터 세트 −

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("Feature names:", feature_names)
print("Target names:", target_names)
print("\nFirst 10 rows of X:\n", X[:10])

산출

Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Target names: ['setosa' 'versicolor' 'virginica']
First 10 rows of X:
[
   [5.1 3.5 1.4 0.2]
   [4.9 3. 1.4 0.2]
   [4.7 3.2 1.3 0.2]
   [4.6 3.1 1.5 0.2]
   [5. 3.6 1.4 0.2]
   [5.4 3.9 1.7 0.4]
   [4.6 3.4 1.4 0.3]
   [5. 3.4 1.5 0.2]
   [4.4 2.9 1.4 0.2]
   [4.9 3.1 1.5 0.1]
]

데이터 세트 분할

모델의 정확성을 확인하기 위해 데이터 세트를 두 부분으로 나눌 수 있습니다.a training set 과 a testing set. 학습 세트를 사용하여 모델을 학습시키고 테스트 세트를 사용하여 모델을 테스트합니다. 그 후 모델이 얼마나 잘했는지 평가할 수 있습니다.

예

다음 예제는 데이터를 70:30 비율로 분할합니다. 즉, 70 % 데이터는 학습 데이터로 사용되고 30 %는 테스트 데이터로 사용됩니다. 데이터 셋은 위의 예에서와 같이 홍채 데이터 셋입니다.

from sklearn.datasets import load_iris
iris = load_iris()

X = iris.data
y = iris.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
   X, y, test_size = 0.3, random_state = 1
)

print(X_train.shape)
print(X_test.shape)

print(y_train.shape)
print(y_test.shape)

산출

(105, 4)
(45, 4)
(105,)
(45,)

위의 예에서 볼 수 있듯이 train_test_split()데이터 세트를 분할하는 scikit-learn의 기능. 이 함수에는 다음 인수가 있습니다.

• X, y − 여기, X 이다 feature matrix 그리고 y는 response vector, 분할해야합니다.

• test_size− 주어진 데이터 전체에 대한 테스트 데이터의 비율을 나타냅니다. 위의 예에서와 같이test_data = 0.3 X의 150 행에 대해. 150 * 0.3 = 45 행의 테스트 데이터를 생성합니다.

• random_size− 분할이 항상 동일 함을 보장하기 위해 사용됩니다. 이는 재현 가능한 결과를 원하는 상황에서 유용합니다.

모델 훈련

다음으로 데이터 세트를 사용하여 예측 모델을 학습시킬 수 있습니다. 논의한 바와 같이 scikit-learn은Machine Learning (ML) algorithms 피팅, 정확도 예측, 리콜 등을위한 일관된 인터페이스가 있습니다.

예

아래 예에서는 KNN (K 개의 최근 접 이웃) 분류기를 사용할 것입니다. KNN 알고리즘에 대해서는 별도의 장이 있으므로 자세히 설명하지 마십시오. 이 예제는 구현 부분 만 이해하는 데 사용됩니다.

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
   X, y, test_size = 0.4, random_state=1
)
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classifier_knn = KNeighborsClassifier(n_neighbors = 3)
classifier_knn.fit(X_train, y_train)
y_pred = classifier_knn.predict(X_test)
# Finding accuracy by comparing actual response values(y_test)with predicted response value(y_pred)
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
# Providing sample data and the model will make prediction out of that data

sample = [[5, 5, 3, 2], [2, 4, 3, 5]]
preds = classifier_knn.predict(sample)
pred_species = [iris.target_names[p] for p in preds] print("Predictions:", pred_species)

산출

Accuracy: 0.9833333333333333
Predictions: ['versicolor', 'virginica']

모델 지속성

모델을 학습 한 후에는 나중에 다시 사용할 필요가 없도록 모델을 유지하는 것이 바람직합니다. 그것은 도움으로 할 수 있습니다dump 과 load 의 특징 joblib 꾸러미.

향후 사용을 위해 위의 훈련 된 모델 (classifier_knn)을 저장할 아래의 예를 고려하십시오.

from sklearn.externals import joblib
joblib.dump(classifier_knn, 'iris_classifier_knn.joblib')

위의 코드는 모델을 iris_classifier_knn.joblib라는 파일에 저장합니다. 이제 다음 코드를 사용하여 파일에서 객체를 다시로드 할 수 있습니다.

joblib.load('iris_classifier_knn.joblib')

데이터 전처리

우리는 많은 데이터를 다루고 있고 그 데이터는 원시 형태이기 때문에 해당 데이터를 기계 학습 알고리즘에 입력하기 전에 의미있는 데이터로 변환해야합니다. 이 프로세스를 데이터 전처리라고합니다. Scikit-learn에는preprocessing이 목적을 위해. 그만큼preprocessing 패키지에는 다음과 같은 기술이 있습니다.

이진화

이 전처리 기술은 숫자 값을 부울 값으로 변환해야 할 때 사용됩니다.

예

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [2.1, -1.9, 5.5],
   [-1.5, 2.4, 3.5],
   [0.5, -7.9, 5.6],
   [5.9, 2.3, -5.8]]
)
data_binarized = preprocessing.Binarizer(threshold=0.5).transform(input_data)
print("\nBinarized data:\n", data_binarized)

위의 예에서 우리는 threshold value = 0.5이므로 0.5 이상의 모든 값은 1로 변환되고 0.5 미만의 모든 값은 0으로 변환됩니다.

산출

Binarized data:
[
   [ 1. 0. 1.]
   [ 0. 1. 1.]
   [ 0. 0. 1.]
   [ 1. 1. 0.]
]

평균 제거

이 기술은 모든 특성이 0에 집중되도록 특성 벡터에서 평균을 제거하는 데 사용됩니다.

예

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [2.1, -1.9, 5.5],
   [-1.5, 2.4, 3.5],
   [0.5, -7.9, 5.6],
   [5.9, 2.3, -5.8]]
)

#displaying the mean and the standard deviation of the input data
print("Mean =", input_data.mean(axis=0))
print("Stddeviation = ", input_data.std(axis=0))
#Removing the mean and the standard deviation of the input data

data_scaled = preprocessing.scale(input_data)
print("Mean_removed =", data_scaled.mean(axis=0))
print("Stddeviation_removed =", data_scaled.std(axis=0))

산출

Mean = [ 1.75 -1.275 2.2 ]
Stddeviation = [ 2.71431391 4.20022321 4.69414529]
Mean_removed = [ 1.11022302e-16 0.00000000e+00 0.00000000e+00]
Stddeviation_removed = [ 1. 1. 1.]

스케일링

이 전처리 기술을 사용하여 특징 벡터의 크기를 조정합니다. 특성이 종합적으로 크거나 작 으면 안되므로 특성 벡터의 크기 조정이 중요합니다.

예

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [
      [2.1, -1.9, 5.5],
      [-1.5, 2.4, 3.5],
      [0.5, -7.9, 5.6],
      [5.9, 2.3, -5.8]
   ]
)
data_scaler_minmax = preprocessing.MinMaxScaler(feature_range=(0,1))
data_scaled_minmax = data_scaler_minmax.fit_transform(input_data)
print ("\nMin max scaled data:\n", data_scaled_minmax)

산출

Min max scaled data:
[
   [ 0.48648649 0.58252427 0.99122807]
   [ 0. 1. 0.81578947]
   [ 0.27027027 0. 1. ]
   [ 1. 0.99029126 0. ]
]

표준화

특징 벡터를 수정하기 위해이 전처리 기술을 사용합니다. 특징 벡터를 공통 스케일로 측정하려면 특징 벡터의 정규화가 필요합니다. 다음과 같이 두 가지 유형의 정규화가 있습니다.

L1 정규화

최소 절대 편차라고도합니다. 절대 값의 합이 항상 각 행에서 최대 1로 유지되도록 값을 수정합니다. 다음 예제는 입력 데이터에 대한 L1 정규화 구현을 보여줍니다.

예

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [
      [2.1, -1.9, 5.5],
      [-1.5, 2.4, 3.5],
      [0.5, -7.9, 5.6],
      [5.9, 2.3, -5.8]
   ]
)
data_normalized_l1 = preprocessing.normalize(input_data, norm='l1')
print("\nL1 normalized data:\n", data_normalized_l1)

산출

L1 normalized data:
[
   [ 0.22105263 -0.2 0.57894737]
   [-0.2027027 0.32432432 0.47297297]
   [ 0.03571429 -0.56428571 0.4 ]
   [ 0.42142857 0.16428571 -0.41428571]
]

L2 정규화

최소 제곱이라고도합니다. 제곱의 합이 각 행에서 항상 1까지 유지되도록 값을 수정합니다. 다음 예제는 입력 데이터에 대한 L2 정규화 구현을 보여줍니다.

예

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [
      [2.1, -1.9, 5.5],
      [-1.5, 2.4, 3.5],
      [0.5, -7.9, 5.6],
      [5.9, 2.3, -5.8]
   ]
)
data_normalized_l2 = preprocessing.normalize(input_data, norm='l2')
print("\nL1 normalized data:\n", data_normalized_l2)

산출

L2 normalized data:
[
   [ 0.33946114 -0.30713151 0.88906489]
   [-0.33325106 0.53320169 0.7775858 ]
   [ 0.05156558 -0.81473612 0.57753446]
   [ 0.68706914 0.26784051 -0.6754239 ]
]

기계 학습이 데이터에서 모델을 생성하려고한다는 것을 알고 있습니다. 이를 위해 컴퓨터는 먼저 데이터를 이해해야합니다. 다음으로, 컴퓨터로 이해하기 위해 데이터를 표현하는 다양한 방법에 대해 논의 할 것입니다.

테이블로 데이터

Scikit-learn에서 데이터를 표현하는 가장 좋은 방법은 테이블 형식입니다. 테이블은 행이 데이터 세트의 개별 요소를 나타내고 열이 해당 개별 요소와 관련된 수량을 나타내는 2D 데이터 그리드를 나타냅니다.

예

아래 주어진 예를 사용하여 iris dataset 파이썬의 도움으로 Pandas DataFrame의 형태로 seaborn 도서관.

import seaborn as sns
iris = sns.load_dataset('iris')
iris.head()

산출

sepal_length sepal_width petal_length petal_width  species
0        5.1      3.5         1.4             0.2   setosa
1        4.9      3.0         1.4             0.2   setosa
2        4.7      3.2         1.3             0.2   setosa
3        4.6      3.1         1.5             0.2   setosa
4        5.0      3.6         1.4             0.2   setosa

위의 출력에서 ​​데이터의 각 행은 관찰 된 단일 꽃을 나타내고 행 수는 데이터 세트의 총 꽃 수를 나타냅니다. 일반적으로 행렬의 행을 샘플이라고합니다.

반면에 데이터의 각 열은 각 샘플을 설명하는 정량적 정보를 나타냅니다. 일반적으로 행렬의 열을 특성이라고합니다.

기능 매트릭스로서의 데이터

특징 행렬은 정보를 2 차원 행렬로 생각할 수있는 테이블 레이아웃으로 정의 할 수 있습니다. 이름이 지정된 변수에 저장됩니다.X모양이 [n_samples, n_features] 인 2 차원이라고 가정합니다. 대부분 NumPy 배열 또는 Pandas DataFrame에 포함됩니다. 앞서 말했듯이 샘플은 항상 데이터 세트에서 설명하는 개별 개체를 나타내고 기능은 각 샘플을 정량적으로 설명하는 별개의 관찰을 나타냅니다.

타겟 어레이로서의 데이터

X로 표시되는 기능 매트릭스와 함께 대상 배열도 있습니다. 레이블이라고도합니다. y로 표시됩니다. 레이블 또는 대상 배열은 일반적으로 길이가 n_samples 인 1 차원입니다. 일반적으로 NumPy에 포함되어 있습니다.array 또는 판다 Series. 대상 배열에는 값, 연속 숫자 값 및 불연속 값이 모두있을 수 있습니다.

타겟 어레이는 특성 열과 어떻게 다릅니 까?

대상 배열이 일반적으로 데이터에서 예측하려는 수량이라는 점을 한 점으로 구분할 수 있습니다. 즉, 통계적 측면에서 종속 변수입니다.

예

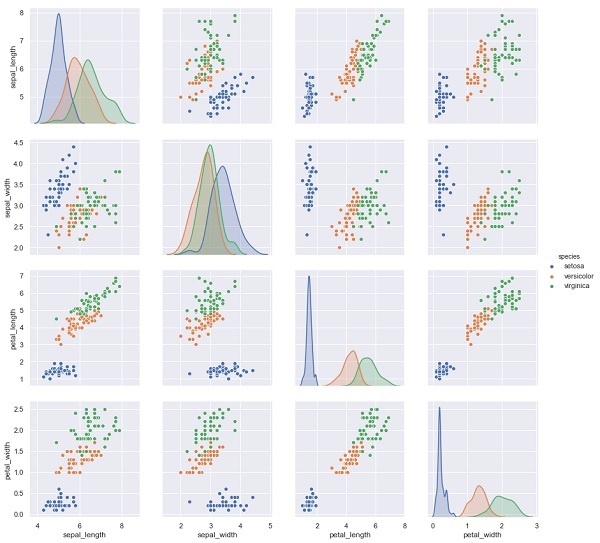
아래 예에서 홍채 데이터 세트에서 다른 측정 값을 기반으로 꽃의 종을 예측합니다. 이 경우 종 열이 기능으로 간주됩니다.

import seaborn as sns
iris = sns.load_dataset('iris')
%matplotlib inline
import seaborn as sns; sns.set()
sns.pairplot(iris, hue='species', height=3);

산출

X_iris = iris.drop('species', axis=1)
X_iris.shape
y_iris = iris['species']
y_iris.shape

산출

(150,4)
(150,)

이 장에서 우리는 Estimator API(응용 프로그래밍 인터페이스). Estimator API가 무엇인지 이해하는 것으로 시작하겠습니다.

Estimator API 란?

Scikit-learn에서 구현 한 주요 API 중 하나입니다. 광범위한 ML 애플리케이션에 일관된 인터페이스를 제공하므로 Scikit-Learn의 모든 기계 학습 알고리즘이 Estimator API를 통해 구현됩니다. 데이터에서 학습하는 객체 (데이터 피팅)는 추정자입니다. 분류, 회귀, 클러스터링과 같은 모든 알고리즘 또는 원시 데이터에서 유용한 기능을 추출하는 변환기와 함께 사용할 수 있습니다.

데이터를 맞추기 위해 모든 추정기 객체는 다음과 같이 데이터 세트를 취하는 적합 방법을 노출합니다.

estimator.fit(data)

다음으로 추정 자의 모든 매개 변수는 해당 속성에 의해 인스턴스화 될 때 다음과 같이 설정 될 수 있습니다.

estimator = Estimator (param1=1, param2=2)
estimator.param1

위의 출력은 1이됩니다.

데이터에 추정기가 장착되면 해당 데이터에서 매개 변수가 추정됩니다. 이제 모든 추정 된 매개 변수는 다음과 같이 밑줄로 끝나는 추정기 객체의 속성이됩니다.

estimator.estimated_param_

Estimator API 사용

추정기의 주요 용도는 다음과 같습니다.

모델 추정 및 디코딩

Estimator 객체는 모델의 추정 및 디코딩에 사용됩니다. 또한 모델은 다음과 같은 결정 론적 함수로 추정됩니다.

• 개체 생성에 제공되는 매개 변수입니다.

• 추정 자의 random_state 매개 변수가 none으로 설정된 경우 전역 임의 상태 (numpy.random)입니다.

• 에 대한 가장 최근 호출에 전달 된 모든 데이터 fit, fit_transform, or fit_predict.

• 일련의 호출에서 전달 된 모든 데이터 partial_fit.

직사각형이 아닌 데이터 표현을 직사각형 데이터로 매핑

직사각형이 아닌 데이터 표현을 직사각형 데이터로 매핑합니다. 간단히 말해서, 각 샘플이 고정 길이의 배열 형 객체로 표현되지 않는 입력을 받아 각 샘플에 대해 배열 형 특징 객체를 생성합니다.

핵심 샘플과 외부 샘플의 구별

다음과 같은 방법을 사용하여 핵심 샘플과 외부 샘플 간의 차이를 모델링합니다.

• fit

• transductive 인 경우 fit_predict

• 귀납적인지 예측

지도 원칙

Scikit-Learn API를 설계하는 동안 명심해야 할 지침 원칙을 따릅니다.

일관성

이 원칙은 모든 개체가 제한된 메서드 집합에서 가져온 공통 인터페이스를 공유해야 함을 나타냅니다. 문서도 일관성이 있어야합니다.

제한된 개체 계층

이지도 원리는 다음과 같습니다.

• 알고리즘은 Python 클래스로 표현되어야합니다.

• 데이터 세트는 NumPy 배열, Pandas DataFrames, SciPy 희소 행렬과 같은 표준 형식으로 표시되어야합니다.

• 매개 변수 이름은 표준 Python 문자열을 사용해야합니다.

구성

우리가 알고 있듯이 ML 알고리즘은 많은 기본 알고리즘의 시퀀스로 표현할 수 있습니다. Scikit-learn은 필요할 때마다 이러한 기본 알고리즘을 사용합니다.

합리적인 기본값

이 원칙에 따라 Scikit-learn 라이브러리는 ML 모델에 사용자 지정 매개 변수가 필요할 때마다 적절한 기본값을 정의합니다.

검사

이 안내 원칙에 따라 지정된 모든 매개 변수 값이 음모 속성으로 노출됩니다.

Estimator API 사용 단계

다음은 Scikit-Learn 추정기 API를 사용하는 단계입니다.

1 단계 : 모델 클래스 선택

이 첫 번째 단계에서는 모델 클래스를 선택해야합니다. Scikit-learn에서 적절한 Estimator 클래스를 가져 와서 수행 할 수 있습니다.

2 단계 : 모델 초 매개 변수 선택

이 단계에서는 클래스 모델 하이퍼 파라미터를 선택해야합니다. 원하는 값으로 클래스를 인스턴스화하여 수행 할 수 있습니다.

3 단계 : 데이터 정렬

다음으로 데이터를 특성 행렬 (X)과 대상 벡터 (y)로 정렬해야합니다.

4 단계 : 모델 피팅

이제 모델을 데이터에 맞아야합니다. 모델 인스턴스의 fit () 메서드를 호출하면됩니다.

5 단계 : 모델 적용

모델을 피팅 한 후 새 데이터에 적용 할 수 있습니다. 지도 학습의 경우predict()알려지지 않은 데이터에 대한 레이블을 예측하는 방법. 비지도 학습의 경우predict() 또는 transform() 데이터의 속성을 추론합니다.

지도 학습 예

여기서는이 프로세스의 예로서 (x, y) 데이터에 선을 맞추는 일반적인 경우를 사용합니다. simple linear regression.

먼저 데이터 세트를로드해야합니다. 홍채 데이터 세트를 사용합니다.

예

import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape

산출

(150, 4)

예

y_iris = iris['species']
y_iris.shape

산출

(150,)

예

이제이 회귀 예제에서는 다음 샘플 데이터를 사용합니다.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);

산출

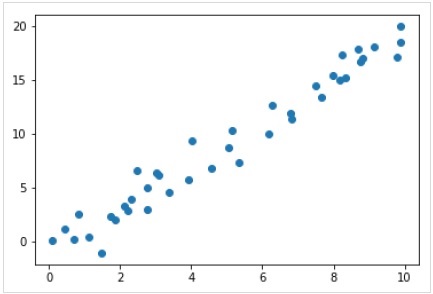
따라서 선형 회귀 예제에 대한 위의 데이터가 있습니다.

이제이 데이터를 사용하여 위에서 언급 한 단계를 적용 할 수 있습니다.

모델 등급 선택

여기서 간단한 선형 회귀 모델을 계산하려면 다음과 같이 선형 회귀 클래스를 가져와야합니다.

from sklearn.linear_model import LinearRegression

모델 하이퍼 파라미터 선택

모델 클래스를 선택한 후에는 종종 하이퍼 파라미터로 표시되는 몇 가지 중요한 선택이나 모델이 데이터에 적합하기 전에 설정해야하는 파라미터를 선택해야합니다. 여기에서이 선형 회귀 예제의 경우 다음을 사용하여 절편을 피팅하려고합니다.fit_intercept 다음과 같이 하이퍼 파라미터-

Example

model = LinearRegression(fit_intercept = True)
model

Output

LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None, normalize = False)

데이터 정렬

이제 목표 변수가 y 올바른 형태, 즉 길이 n_samples1 차원 배열. 하지만 특성 매트릭스를 재구성해야합니다.X 크기의 행렬로 만들려면 [n_samples, n_features]. 다음과 같이 할 수 있습니다-

Example

X = x[:, np.newaxis]
X.shape

Output

(40, 1)

모델 피팅

일단 데이터를 정렬하면 모델을 맞출 시간입니다. 즉, 모델을 데이터에 적용 할 때입니다. 이것은 다음의 도움으로 수행 될 수 있습니다.fit() 다음과 같이 방법-

Example

model.fit(X, y)

Output

LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None,normalize = False)

Scikit-learn에서 fit() 프로세스에는 후행 밑줄이 있습니다.

이 예에서 아래 매개 변수는 데이터의 단순 선형 적합 기울기를 보여줍니다.

Example

model.coef_

Output

array([1.99839352])

아래 매개 변수는 데이터에 대한 단순 선형 피팅의 절편을 나타냅니다.

Example

model.intercept_

Output

-0.9895459457775022

새 데이터에 모델 적용

모델을 학습 한 후 새 데이터에 적용 할 수 있습니다. 지도 머신 러닝의 주요 임무는 학습 세트의 일부가 아닌 새로운 데이터를 기반으로 모델을 평가하는 것입니다. 그것은 도움으로 할 수 있습니다predict() 다음과 같이 방법-

Example

xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);

Output

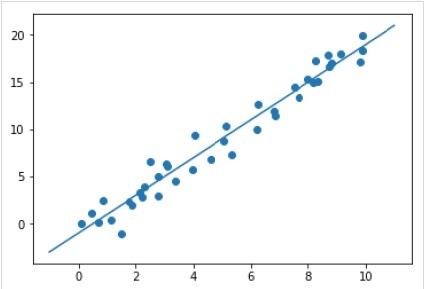
완전한 작업 / 실행 가능한 예

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape

rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model
X = x[:, np.newaxis]
X.shape

model.fit(X, y)
model.coef_
model.intercept_

xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);

비지도 학습 예

여기서는이 프로세스의 예로서 Iris 데이터 세트의 차원을 줄이는 일반적인 경우를 사용하여보다 쉽게 ​​시각화 할 수 있습니다. 이 예에서는 빠른 선형 차원 감소 기술인 주성분 분석 (PCA)을 사용합니다.

위의 예와 같이 홍채 데이터 세트에서 임의의 데이터를로드하고 플로팅 할 수 있습니다. 그 후 다음 단계를 따를 수 있습니다.

모델 등급 선택

from sklearn.decomposition import PCA

모델 하이퍼 파라미터 선택

Example

model = PCA(n_components=2)
model

Output

PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
   svd_solver = 'auto', tol = 0.0, whiten = False)

모델 피팅

Example

model.fit(X_iris)

Output

PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
   svd_solver = 'auto', tol = 0.0, whiten = False)

데이터를 2 차원으로 변환

Example

X_2D = model.transform(X_iris)

이제 결과를 다음과 같이 그릴 수 있습니다.

Output

iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue = 'species', data = iris, fit_reg = False);

Output

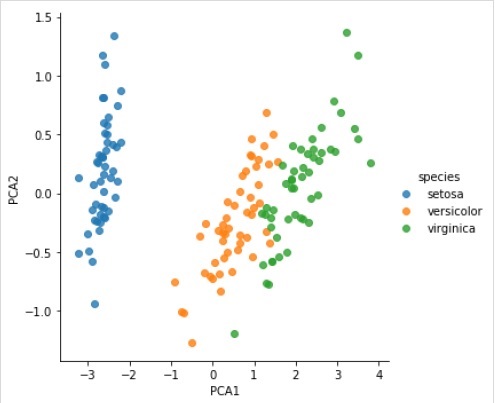
완전한 작업 / 실행 가능한 예

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.decomposition import PCA

model = PCA(n_components=2)
model
model.fit(X_iris)
X_2D = model.transform(X_iris)
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);

Scikit-learn의 객체는 다음 세 가지 보완 인터페이스로 구성된 균일 한 기본 API를 공유합니다.

• Estimator interface − 모델 구축 및 피팅을위한 것입니다.

• Predictor interface − 예측하기위한 것입니다.

• Transformer interface − 데이터 변환 용입니다.

API는 간단한 규칙을 채택하고 디자인 선택은 프레임 워크 코드의 확산을 방지하는 방식으로 안내되었습니다.

협약의 목적

관례의 목적은 API가 다음과 같은 광범위한 원칙을 준수하도록하는 것입니다.

Consistency − 기본이든 합성이든 모든 객체는 제한된 메소드 세트로 더 구성된 일관된 인터페이스를 공유해야합니다.

Inspection − 학습 알고리즘에 의해 결정된 생성자 매개 변수 및 매개 변수 값은 공개 속성으로 저장 및 노출되어야합니다.

Non-proliferation of classes − 데이터 세트는 NumPy 배열 또는 Scipy 희소 행렬로 표시되어야하지만 하이퍼 매개 변수 이름과 값은 프레임 워크 코드의 확산을 피하기 위해 표준 Python 문자열로 표시되어야합니다.

Composition − 데이터에 대한 변환의 시퀀스 또는 조합으로 표현할 수 있는지 또는 다른 알고리즘에서 매개 변수화 된 메타 알고리즘으로 자연스럽게 보이는 알고리즘은 기존 빌딩 블록으로 구현되고 구성되어야합니다.

Sensible defaults− scikit-learn에서는 작업에 사용자 정의 매개 변수가 필요할 때마다 적절한 기본값이 정의됩니다. 이 기본값은 작업이 현명한 방식으로 수행되도록해야합니다 (예 : 현재 작업에 대한 기준 솔루션 제공).

다양한 컨벤션

Sklearn에서 사용 가능한 규칙은 아래에 설명되어 있습니다.

유형 캐스팅

입력이 캐스트되어야 함을 나타냅니다. float64. 다음 예에서sklearn.random_projection 데이터의 차원을 줄이는 데 사용되는 모듈에 대해 설명합니다.

Example

import numpy as np
from sklearn import random_projection
rannge = np.random.RandomState(0)
X = range.rand(10,2000)
X = np.array(X, dtype = 'float32')
X.dtype
Transformer_data = random_projection.GaussianRandomProjection()
X_new = transformer.fit_transform(X)
X_new.dtype

Output

dtype('float32')
dtype('float64')

위의 예에서 X가 float32 캐스팅 float64 으로 fit_transform(X).

매개 변수 재조정 및 업데이트

추정기의 하이퍼 파라미터는 다음을 통해 구성된 후 업데이트 및 재구성 될 수 있습니다. set_params()방법. 그것을 이해하기 위해 다음 예제를 보자-

Example

import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])

Output

array([0, 0, 0, 0, 0])

추정기가 구성되면 위의 코드가 기본 커널을 변경합니다. rbf 선형 비아로 SVC.set_params().

이제 다음 코드는 커널을 다시 rbf로 변경하여 추정기를 다시 맞추고 두 번째 예측을 수행합니다.

Example

clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])

Output

array([0, 0, 0, 0, 0])

완전한 코드

다음은 완전한 실행 프로그램입니다-

import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])

다중 클래스 및 다중 레이블 피팅

다중 클래스 피팅의 경우 학습 및 예측 작업은 모두 맞는 대상 데이터의 형식에 따라 다릅니다. 사용 된 모듈은 다음과 같습니다.sklearn.multiclass. 다중 클래스 분류 기가 1d 배열에 맞는 아래 예제를 확인하십시오.

Example

from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = [0, 0, 1, 1, 2]
classif = OneVsRestClassifier(estimator = SVC(gamma = 'scale',random_state = 0))
classif.fit(X, y).predict(X)

Output

array([0, 0, 1, 1, 2])

위의 예에서 분류자는 다중 클래스 레이블의 1 차원 배열에 적합하며 predict()따라서 메서드는 해당 다중 클래스 예측을 제공합니다. 그러나 다른 한편으로 다음과 같이 이진 레이블 표시기의 2 차원 배열에 맞출 수도 있습니다.

Example

from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = LabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)

Output

array(
   [
      [0, 0, 0],
      [0, 0, 0],
      [0, 1, 0],
      [0, 1, 0],
      [0, 0, 0]
   ]
)

마찬가지로 다중 레이블 피팅의 경우 다음과 같이 인스턴스에 여러 레이블을 할당 할 수 있습니다.

Example

from sklearn.preprocessing import MultiLabelBinarizer
y = [[0, 1], [0, 2], [1, 3], [0, 2, 3], [2, 4]]
y = MultiLabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)

Output

array(
   [
      [1, 0, 1, 0, 0],
      [1, 0, 1, 0, 0],
      [1, 0, 1, 1, 0],
      [1, 0, 1, 1, 0],
      [1, 0, 1, 0, 0]
   ]
)

위의 예에서 sklearn.MultiLabelBinarizer맞추기 위해 다중 레이블의 2 차원 배열을 이진화하는 데 사용됩니다. 이것이 predict () 함수가 각 인스턴스에 대해 여러 레이블이있는 출력으로 2d 배열을 제공하는 이유입니다.

이 장은 Scikit-Learn의 선형 모델링에 대해 배우는 데 도움이 될 것입니다. Sklearn에서 선형 회귀가 무엇인지 이해하는 것으로 시작하겠습니다.

다음 표는 Scikit-Learn에서 제공하는 다양한 선형 모델을 나열합니다.

Sr. 아니요	모델 및 설명
1	선형 회귀 주어진 독립 변수 세트 (X)와 종속 변수 (Y) 간의 관계를 연구하는 최고의 통계 모델 중 하나입니다.
2	로지스틱 회귀 로지스틱 회귀는 이름에도 불구하고 회귀 알고리즘이 아닌 분류 알고리즘입니다. 주어진 독립 변수 세트를 기반으로 이산 값 (0 또는 1, 예 / 아니오, 참 / 거짓)을 추정하는 데 사용됩니다.
삼	릿지 회귀 Ridge 회귀 또는 Tikhonov 정규화는 L2 정규화를 수행하는 정규화 기술입니다. 계수 크기의 제곱에 해당하는 패널티 (수축량)를 추가하여 손실 함수를 수정합니다.
4	베이지안 능선 회귀 베이지안 회귀는 포인트 추정이 아닌 확률 분포를 사용하여 선형 회귀를 공식화함으로써 불충분 한 데이터 또는 불충분하게 분산 된 데이터를 자연 메커니즘으로 유지합니다.
5	올가미 LASSO는 L1 정규화를 수행하는 정규화 기술입니다. 계수의 절대 값의 합에 해당하는 패널티 (수축량)를 추가하여 손실 함수를 수정합니다.
6	멀티 태스킹 LASSO 작업이라고도하는 모든 회귀 문제에 대해 선택한 기능을 동일하게 적용하도록 여러 회귀 문제에 맞출 수 있습니다. Sklearn은 다중 회귀 문제에 대한 희소 계수를 공동으로 추정하는 정규화를 위해 혼합 L1, L2- 노름으로 훈련 된 MultiTaskLasso라는 선형 모델을 제공합니다.
7	Elastic-Net Elastic-Net은 Lasso 및 Ridge 회귀 방법의 L1 및 L2와 같은 두 패널티를 선형 적으로 결합하는 정규화 된 회귀 방법입니다. 상호 관련된 기능이 여러 개있을 때 유용합니다.
8	멀티 태스킹 Elastic-Net 작업이라고도하는 모든 회귀 문제에 대해 선택한 기능을 동일하게 적용하여 여러 회귀 문제에 맞출 수있는 Elastic-Net 모델입니다.

이 장에서는 Sklearn의 다항식 기능과 파이프 라이닝 도구에 중점을 둡니다.

다항식 기능 소개

데이터의 비선형 함수에 대해 훈련 된 선형 모델은 일반적으로 선형 방법의 빠른 성능을 유지합니다. 또한 훨씬 더 광범위한 데이터에 맞출 수 있습니다. 이것이 기계 학습에서 비선형 함수에 대해 훈련 된 선형 모델이 사용되는 이유입니다.

이러한 예 중 하나는 계수에서 다항식 특징을 구성하여 단순 선형 회귀를 확장 할 수 있다는 것입니다.

수학적으로 표준 선형 회귀 모델이 있다고 가정하면 2D 데이터의 경우 다음과 같습니다.

$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}$$

이제 우리는 2 차 다항식의 특징을 결합 할 수 있으며 모델은 다음과 같이 보일 것입니다.

$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{1}X_{2}+W_{4}X_1^2+W_{5}X_2^2$$

위는 여전히 선형 모델입니다. 여기서 우리는 결과 다항 회귀가 동일한 선형 모델 클래스에 있으며 유사하게 풀 수 있음을 확인했습니다.

이를 위해 scikit-learn은 PolynomialFeatures. 이 모듈은 입력 데이터 매트릭스를 주어진 정도의 새로운 데이터 매트릭스로 변환합니다.

매개 변수

다음 표는 PolynomialFeatures 기준 치수

Sr. 아니요	매개 변수 및 설명
1	degree − 정수, 기본값 = 2 다항식 기능의 정도를 나타냅니다.
2	interaction_only − 부울, 기본값 = false 기본적으로 false이지만 true로 설정되면 대부분의 고유 한 입력 기능의 제품인 기능이 생성됩니다. 이러한 기능을 상호 작용 기능이라고합니다.
삼	include_bias − 부울, 기본값 = true 여기에는 바이어스 열, 즉 모든 다항식 거듭 제곱이 0 인 기능이 포함됩니다.
4	order − str in { 'C', 'F'}, 기본값 = 'C' 이 매개 변수는 고밀도 케이스에서 출력 배열의 순서를 나타냅니다. 'F'순서는 계산 속도가 더 빠르다는 것을 의미하지만 다른 한편으로 후속 견적을 늦출 수 있습니다.

속성

다음 표는에서 사용하는 속성으로 구성됩니다. PolynomialFeatures 기준 치수

Sr. 아니요	속성 및 설명
1	powers_ − 배열, 모양 (n_output_features, n_input_features) powers_ [i, j]가 i 번째 출력에서 ​​j 번째 입력의 지수임을 보여줍니다.
2	n_input_features _ − 정수 이름에서 알 수 있듯이 총 입력 기능 수를 제공합니다.
삼	n_output_features _ − 정수 이름에서 알 수 있듯이 총 다항식 출력 기능 수를 제공합니다.

구현 예

다음 Python 스크립트 사용 PolynomialFeatures 8의 배열을 (4,2) 형태로 변환하는 변환기 −

from sklearn.preprocessing import PolynomialFeatures
import numpy as np
Y = np.arange(8).reshape(4, 2)
poly = PolynomialFeatures(degree=2)
poly.fit_transform(Y)

산출

array(
   [
      [ 1., 0., 1., 0., 0., 1.],
      [ 1., 2., 3., 4., 6., 9.],
      [ 1., 4., 5., 16., 20., 25.],
      [ 1., 6., 7., 36., 42., 49.]
   ]
)

파이프 라인 도구를 사용하여 간소화

위와 같은 종류의 전처리, 즉 입력 데이터 매트릭스를 주어진 정도의 새로운 데이터 매트릭스로 변환하는 것은 다음과 같이 간소화 할 수 있습니다. Pipeline 기본적으로 여러 추정치를 하나로 연결하는 데 사용되는 도구입니다.

예

Scikit-learn의 파이프 라인 도구를 사용하여 전처리를 간소화하는 아래 Python 스크립트 (차수 3 다항식 데이터에 적합).

#First, import the necessary packages.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np

#Next, create an object of Pipeline tool
Stream_model = Pipeline([('poly', PolynomialFeatures(degree=3)), ('linear', LinearRegression(fit_intercept=False))])

#Provide the size of array and order of polynomial data to fit the model.
x = np.arange(5)
y = 3 - 2 * x + x ** 2 - x ** 3
Stream_model = model.fit(x[:, np.newaxis], y)

#Calculate the input polynomial coefficients.
Stream_model.named_steps['linear'].coef_

산출

array([ 3., -2., 1., -1.])

위의 출력은 다항식 기능에 대해 훈련 된 선형 모델이 정확한 입력 다항식 계수를 복구 할 수 있음을 보여줍니다.

여기서는 SGD (Stochastic Gradient Descent)라고하는 Sklearn의 최적화 알고리즘에 대해 알아 봅니다.

확률 적 경사 하강 법 (SGD)은 비용 함수를 최소화하는 함수의 매개 변수 / 계수 값을 찾는 데 사용되는 간단하면서도 효율적인 최적화 알고리즘입니다. 즉, SVM 및 로지스틱 회귀와 같은 볼록 손실 함수에서 선형 분류기의 차별적 학습에 사용됩니다. 계수 업데이트는 인스턴스 끝이 아닌 각 학습 인스턴스에 대해 수행되기 때문에 대규모 데이터 세트에 성공적으로 적용되었습니다.

SGD 분류 자

SGD (Stochastic Gradient Descent) 분류기는 기본적으로 다양한 손실 함수 및 분류 페널티를 지원하는 일반 SGD 학습 루틴을 구현합니다. Scikit-learn은SGDClassifier SGD 분류를 구현하는 모듈.

매개 변수

다음 표는 SGDClassifier 모듈-

Sr. 아니요	매개 변수 및 설명
1	loss − str, 기본값 = 'hinge' 구현하는 동안 사용할 손실 함수를 나타냅니다. 기본값은 선형 SVM을 제공하는 '힌지'입니다. 사용할 수있는 다른 옵션은 다음과 같습니다. log −이 손실은 로지스틱 회귀, 즉 확률 적 분류기를 제공합니다. modified_huber − 확률 추정치와 함께 특이 치에 대한 내성을 가져 오는 부드러운 손실. squared_hinge − '힌지'손실과 유사하지만 2 차적으로 페널티를받습니다. perceptron − 이름에서 알 수 있듯이 퍼셉트론 알고리즘에서 사용하는 선형 손실입니다.
2	penalty − str, 'none', 'l2', 'l1', 'elasticnet' 모델에서 사용되는 정규화 용어입니다. 기본적으로 L2입니다. L1 또는 'elasticnet을 사용할 수 있습니다. 하지만 둘 다 모델에 희소성을 가져올 수 있으므로 L2에서는 달성 할 수 없습니다.
삼	alpha − 부동, 기본값 = 0.0001 정규화 항을 곱하는 상수 인 알파는 모델에 페널티를 줄 정도를 결정하는 조정 매개 변수입니다. 기본값은 0.0001입니다.
4	l1_ratio − 부동, 기본값 = 0.15 이를 ElasticNet 혼합 매개 변수라고합니다. 범위는 0 <= l1_ratio <= 1입니다. l1_ratio = 1이면 패널티는 L1 패널티가됩니다. l1_ratio = 0이면 패널티는 L2 패널티가됩니다.
5	fit_intercept − 부울, 기본값 = True 이 매개 변수는 결정 함수에 상수 (편향 또는 절편)를 추가해야 함을 지정합니다. 계산에 절편이 사용되지 않으며 false로 설정되면 데이터가 이미 중앙에있는 것으로 간주됩니다.
6	tol − float 또는 none, 선택 사항, 기본값 = 1.e-3 이 매개 변수는 반복의 중지 기준을 나타냅니다. 기본값은 False이지만 None으로 설정하면 반복이 중지됩니다.loss > best_loss - tol for n_iter_no_change연속적인 시대.
7	shuffle − 부울, 옵션, 기본값 = True 이 매개 변수는 훈련 데이터를 각 세대 후에 섞을 것인지 여부를 나타냅니다.
8	verbose − 정수, 기본값 = 0 상세 수준을 나타냅니다. 기본값은 0입니다.
9	epsilon − 부동, 기본값 = 0.1 이 매개 변수는 민감하지 않은 영역의 너비를 지정합니다. loss = 'epsilon-insensitive'이면 현재 예측과 올바른 레이블 간의 차이가 임계 값 미만이면 무시됩니다.
10	max_iter − int, 선택, 기본값 = 1000 이름에서 알 수 있듯이, 이는 훈련 데이터와 같은 epoch에 대한 최대 패스 수를 나타냅니다.
11	warm_start − bool, 선택 사항, 기본값 = false 이 매개 변수를 True로 설정하면 이전 호출의 솔루션을 초기화에 맞게 재사용 할 수 있습니다. 기본값, 즉 false를 선택하면 이전 솔루션이 지워집니다.
12	random_state − int, RandomState 인스턴스 또는 None, 선택 사항, 기본값 = 없음 이 매개 변수는 데이터를 섞는 동안 사용되는 생성 된 의사 난수의 시드를 나타냅니다. 옵션은 다음과 같습니다. int −이 경우 random_state 난수 생성기에서 사용하는 시드입니다. RandomState instance −이 경우 random_state 난수 생성기입니다. None −이 경우 난수 생성기는 np.random에서 사용하는 RandonState 인스턴스입니다.
13	n_jobs − int 또는 none, 선택 사항, 기본값 = None 다중 클래스 문제에 대해 OVA (One Versus All) 계산에 사용되는 CPU 수를 나타냅니다. 기본값은 1을 의미하는 없음입니다.
14	learning_rate − 문자열, 선택 사항, 기본값 = '최적' 학습률이 '상수'이면 eta = eta0; 학습률이 '최적'이면 eta = 1.0 / (alpha * (t + t0)), 여기서 t0은 Leon Bottou가 선택합니다. 학습률 = 'invscalling'이면 eta = eta0 / pow (t, power_t)입니다. 학습률 = '적응 형'이면 eta = eta0입니다.
15	eta0 − double, 기본값 = 0.0 위에서 언급 한 학습률 옵션에 대한 초기 학습률을 나타냅니다. 즉 '상수', 'invscalling'또는 '적응 형'입니다.
16	power_t − idouble, 기본값 = 0.5 '포함'학습률의 지수입니다.
17	early_stopping − bool, 기본값 = False 이 매개 변수는 검증 점수가 개선되지 않을 때 조기 중지를 사용하여 훈련을 종료하는 것을 나타냅니다. 기본값은 false이지만 true로 설정하면 자동으로 계층화 된 학습 데이터 부분을 검증으로 설정하고 검증 점수가 개선되지 않을 때 훈련을 중지합니다.
18	validation_fraction − 부동, 기본값 = 0.1 early_stopping이 참일 때만 사용됩니다. 훈련 데이터의 조기 종료를 위해 검증 세트로 따로 설정할 훈련 데이터의 비율을 나타냅니다.
19	n_iter_no_change − int, 기본값 = 5 조기 중지 전에 알고리즘을 실행해야하는 개선없이 반복 횟수를 나타냅니다.
20	classs_weight − dict, {class_label : weight} 또는 "balanced"또는 None, 선택 사항 이 매개 변수는 클래스와 관련된 가중치를 나타냅니다. 제공되지 않으면 클래스의 가중치는 1로 간주됩니다.
20	warm_start − bool, 선택 사항, 기본값 = false 이 매개 변수를 True로 설정하면 이전 호출의 솔루션을 초기화에 맞게 재사용 할 수 있습니다. 기본값, 즉 false를 선택하면 이전 솔루션이 지워집니다.
21	average − iBoolean 또는 int, 선택 사항, 기본값 = false 다중 클래스 문제에 대해 OVA (One Versus All) 계산에 사용되는 CPU 수를 나타냅니다. 기본값은 1을 의미하는 없음입니다.

속성

다음 표는 SGDClassifier 모듈-

Sr. 아니요	속성 및 설명
1	coef_ − n_classes == 2이면 배열, 모양 (1, n_features), 그렇지 않으면 (n_classes, n_features) 이 속성은 기능에 할당 된 가중치를 제공합니다.
2	intercept_ − 배열, 모양 (1,) if n_classes == 2, else (n_classes,) 결정 기능에서 독립적 인 용어를 나타냅니다.
삼	n_iter_ − 정수 중지 기준에 도달하기위한 반복 횟수를 제공합니다.

Implementation Example

다른 분류기와 마찬가지로 SGD (Stochastic Gradient Descent)는 다음 두 배열에 적합해야합니다.

• 훈련 샘플이 들어있는 배열 X입니다. 크기는 [n_samples, n_features]입니다.

• 목표 값, 즉 훈련 샘플에 대한 클래스 레이블을 보유하는 배열 Y. 크기는 [n_samples]입니다.

Example

다음 Python 스크립트는 SGDClassifier 선형 모델을 사용합니다.

import numpy as np
from sklearn import linear_model
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
Y = np.array([1, 1, 2, 2])
SGDClf = linear_model.SGDClassifier(max_iter = 1000, tol=1e-3,penalty = "elasticnet")
SGDClf.fit(X, Y)

Output

SGDClassifier(
   alpha = 0.0001, average = False, class_weight = None,
   early_stopping = False, epsilon = 0.1, eta0 = 0.0, fit_intercept = True,
   l1_ratio = 0.15, learning_rate = 'optimal', loss = 'hinge', max_iter = 1000,
   n_iter = None, n_iter_no_change = 5, n_jobs = None, penalty = 'elasticnet',
   power_t = 0.5, random_state = None, shuffle = True, tol = 0.001,
   validation_fraction = 0.1, verbose = 0, warm_start = False
)

Example

이제 적합하면 모델은 다음과 같이 새로운 값을 예측할 수 있습니다.

SGDClf.predict([[2.,2.]])

Output

array([2])

Example

위의 예에서 다음 파이썬 스크립트를 사용하여 가중치 벡터를 얻을 수 있습니다.

SGDClf.coef_

Output

array([[19.54811198, 9.77200712]])

Example

유사하게, 우리는 다음 파이썬 스크립트의 도움으로 intercept의 값을 얻을 수 있습니다.

SGDClf.intercept_

Output

array([10.])

Example

다음을 사용하여 초평면까지의 부호있는 거리를 얻을 수 있습니다. SGDClassifier.decision_function 다음 파이썬 스크립트에서 사용 된 것처럼-

SGDClf.decision_function([[2., 2.]])

Output

array([68.6402382])

SGD 회귀 자

SGD (Stochastic Gradient Descent) 회귀 분석기는 기본적으로 선형 회귀 모델에 맞게 다양한 손실 함수와 패널티를 지원하는 일반 SGD 학습 루틴을 구현합니다. Scikit-learn은SGDRegressor SGD 회귀를 구현하는 모듈.

매개 변수

사용 매개 변수 SGDRegressorSGDClassifier 모듈에서 사용 된 것과 거의 동일합니다. 차이점은 '손실'매개 변수에 있습니다. 에 대한SGDRegressor 모듈의 손실 매개 변수 양수 값은 다음과 같습니다.

• squared_loss − 일반 최소 제곱 적합을 나타냅니다.

• huber: SGDRegressor− 엡실론 거리를 지나서 제곱에서 선형 손실로 전환하여 이상 값을 수정합니다. 'huber'의 작업은 알고리즘이 이상 값 수정에 덜 집중하도록 'squared_loss'를 수정하는 것입니다.

• epsilon_insensitive − 실제로는 엡실론보다 적은 오류를 무시합니다.

• squared_epsilon_insensitive− epsilon_insensitive와 동일합니다. 유일한 차이점은 엡실론의 허용 오차를 넘어서 손실의 제곱이된다는 것입니다.

또 다른 차이점은 'power_t'라는 매개 변수의 기본값은 0.5가 아니라 0.25라는 것입니다. SGDClassifier. 또한 'class_weight'및 'n_jobs'매개 변수가 없습니다.

속성

SGDRegressor의 속성도 SGDClassifier 모듈의 속성과 동일합니다. 오히려 다음과 같은 세 가지 추가 속성이 있습니다.

• average_coef_ − 배열, 모양 (n_features,)

이름에서 알 수 있듯이 기능에 할당 된 평균 가중치를 제공합니다.

• average_intercept_ − 배열, 모양 (1,)

이름에서 알 수 있듯이 평균 절편 기간을 제공합니다.

• t_ − 정수

훈련 단계에서 수행 된 가중치 업데이트 수를 제공합니다.

Note − average_coef_ 및 average_intercept_ 속성은 'average'매개 변수를 True로 활성화 한 후에 작동합니다.

Implementation Example

다음 Python 스크립트 사용 SGDRegressor 선형 모델 −

import numpy as np
from sklearn import linear_model
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
SGDReg =linear_model.SGDRegressor(
   max_iter = 1000,penalty = "elasticnet",loss = 'huber',tol = 1e-3, average = True
)
SGDReg.fit(X, y)

Output

SGDRegressor(
   alpha = 0.0001, average = True, early_stopping = False, epsilon = 0.1,
   eta0 = 0.01, fit_intercept = True, l1_ratio = 0.15,
   learning_rate = 'invscaling', loss = 'huber', max_iter = 1000,
   n_iter = None, n_iter_no_change = 5, penalty = 'elasticnet', power_t = 0.25,
   random_state = None, shuffle = True, tol = 0.001, validation_fraction = 0.1,
   verbose = 0, warm_start = False
)

Example

이제 적합하면 다음 파이썬 스크립트의 도움으로 가중치 벡터를 얻을 수 있습니다.

SGDReg.coef_

Output

array([-0.00423314, 0.00362922, -0.00380136, 0.00585455, 0.00396787])

Example

유사하게, 우리는 다음 파이썬 스크립트의 도움으로 intercept의 값을 얻을 수 있습니다.

SGReg.intercept_

Output

SGReg.intercept_

Example

다음 파이썬 스크립트의 도움으로 훈련 단계에서 가중치 업데이트 수를 얻을 수 있습니다.

SGDReg.t_

Output

61.0

SGD의 장단점

SGD의 장점에 따라-

• 확률 적 경사 하강 법 (SGD)은 매우 효율적입니다.

• 코드 튜닝에 대한 많은 기회가 있기 때문에 구현하기가 매우 쉽습니다.

SGD의 단점에 따라-

• SGD (Stochastic Gradient Descent)에는 정규화 매개 변수와 같은 여러 하이퍼 파라미터가 필요합니다.

• 기능 확장에 민감합니다.

이 장에서는 SVM (Support Vector Machine)이라는 기계 학습 방법을 다룹니다.

소개

SVM (Support Vector Machine)은 분류, 회귀 및 이상 값 탐지에 사용되는 강력하면서도 유연한 감독 형 기계 학습 방법입니다. SVM은 고차원 공간에서 매우 효율적이며 일반적으로 분류 문제에 사용됩니다. SVM은 의사 결정 기능에서 훈련 포인트의 하위 집합을 사용하기 때문에 널리 사용되며 메모리 효율적입니다.

SVM의 주요 목표는 데이터 세트를 여러 클래스로 나누는 것입니다. maximum marginal hyperplane (MMH) 다음 두 단계로 수행 할 수 있습니다.

• Support Vector Machines는 먼저 클래스를 최상의 방법으로 분리하는 초평면을 반복적으로 생성합니다.

• 그 후 클래스를 올바르게 분리하는 초평면을 선택합니다.

SVM의 몇 가지 중요한 개념은 다음과 같습니다.

• Support Vectors− 초평면에 가장 가까운 데이터 포인트로 정의 할 수 있습니다. 지원 벡터는 구분선을 결정하는 데 도움이됩니다.

• Hyperplane − 서로 다른 클래스를 가진 개체 집합을 나누는 결정 평면 또는 공간.

• Margin − 서로 다른 클래스의 옷장 데이터 포인트에서 두 줄 사이의 간격을 여백이라고합니다.

다음 다이어그램은 이러한 SVM 개념에 대한 통찰력을 제공합니다.

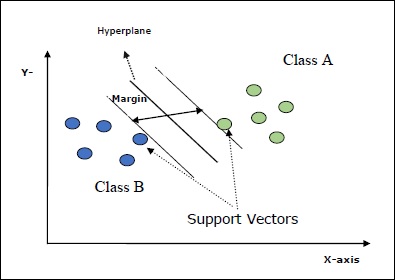
Scikit-learn의 SVM은 희소 및 고밀도 샘플 벡터를 입력으로 모두 지원합니다.

SVM 분류

Scikit-learn은 세 가지 클래스를 제공합니다. SVC, NuSVC 과 LinearSVC 다중 클래스 클래스 분류를 수행 할 수 있습니다.

SVC

구현이 기반으로하는 C 지원 벡터 분류입니다. libsvm. scikit-learn에서 사용하는 모듈은 다음과 같습니다.sklearn.svm.SVC. 이 클래스는 일대일 체계에 따라 다중 클래스 지원을 처리합니다.

매개 변수

다음 표는 sklearn.svm.SVC 클래스-

Sr. 아니요	매개 변수 및 설명
1	C − 부동, 선택, 기본값 = 1.0 오류 항의 페널티 매개 변수입니다.
2	kernel − 문자열, 선택 사항, 기본값 = 'rbf' 이 매개 변수는 알고리즘에서 사용할 커널 유형을 지정합니다. 다음 중 하나를 선택할 수 있습니다.‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. 커널의 기본값은 다음과 같습니다.‘rbf’.
삼	degree − int, 선택, 기본값 = 3 이것은 '다중'커널 기능의 정도를 나타내며 다른 모든 커널에서는 무시됩니다.
4	gamma − { 'scale', 'auto'} 또는 float, 커널 'rbf', 'poly'및 'sigmoid'에 대한 커널 계수입니다.
5	optinal default − = '스케일' 기본값, 즉 gamma = 'scale'을 선택하면 SVC에서 사용할 감마 값은 1 / (_ ∗. ())입니다. 반면 gamma = 'auto'이면 1 / _를 사용합니다.
6	coef0 − 부동, 선택, 기본값 = 0.0 'poly'와 'sigmoid'에서만 중요한 커널 함수의 독립 용어입니다.
7	tol − 부동, 선택, 기본값 = 1.e-3 이 매개 변수는 반복의 중지 기준을 나타냅니다.
8	shrinking − 부울, 옵션, 기본값 = True 이 매개 변수는 축소 휴리스틱 사용 여부를 나타냅니다.
9	verbose − 부울, 기본값 : false 자세한 출력을 활성화하거나 비활성화합니다. 기본값은 false입니다.
10	probability − 부울, 옵션, 기본값 = true 이 매개 변수는 확률 추정을 활성화하거나 비활성화합니다. 기본값은 false이지만 fit을 호출하기 전에 활성화해야합니다.
11	max_iter − int, 선택, 기본값 = -1 이름에서 알 수 있듯이 솔버 내의 최대 반복 횟수를 나타냅니다. 값 -1은 반복 횟수에 제한이 없음을 의미합니다.
12	cache_size − 부동, 선택 사항 이 매개 변수는 커널 캐시의 크기를 지정합니다. 값은 MB (MegaBytes)입니다.
13	random_state − int, RandomState 인스턴스 또는 None, 선택 사항, 기본값 = 없음 이 매개 변수는 데이터를 섞는 동안 사용되는 생성 된 의사 난수의 시드를 나타냅니다. 다음은 옵션입니다- int−이 경우 random_state 는 난수 생성기에서 사용하는 시드입니다. RandomState instance −이 경우 random_state는 난수 생성기입니다. None −이 경우 난수 생성기는 np.random에서 사용하는 RandonState 인스턴스입니다.
14	class_weight − {dict, 'balanced'}, 선택 사항 이 매개 변수는 클래스 j의 매개 변수 C를 SVC에 대해 _ℎ [] *로 설정합니다. 기본 옵션을 사용하면 모든 클래스의 가중치가 1이어야 함을 의미합니다. 반면에 선택하면class_weight:balanced, 자동으로 가중치를 조정하기 위해 y 값을 사용합니다.
15	decision_function_shape − ovo ','ovr ', 기본값 ='ovr ' 이 매개 변수는 알고리즘이 ‘ovr’ (one-vs-rest) 다른 모든 분류기와 같은 형태의 결정 함수 또는 원본 ovo(one-vs-one) libsvm의 결정 기능.
16	break_ties − 부울, 옵션, 기본값 = false True − 예측은 decision_function의 신뢰도 값에 따라 관계를 끊습니다. False − 예측은 동점 클래스 중 첫 번째 클래스를 반환합니다.

속성

다음 표는에서 사용하는 속성으로 구성됩니다. sklearn.svm.SVC 클래스-

Sr. 아니요	속성 및 설명
1	support_ − 배열 형, 모양 = [n_SV] 지원 벡터의 인덱스를 반환합니다.
2	support_vectors_ − 배열 형, 모양 = [n_SV, n_features] 지원 벡터를 반환합니다.
삼	n_support_ − 배열 형, dtype = int32, 모양 = [n_class] 각 클래스에 대한 지원 벡터의 수를 나타냅니다.
4	dual_coef_ − 배열, 모양 = [n_class-1, n_SV] 이것은 결정 함수에서 지원 벡터의 계수입니다.
5	coef_ − 배열, 모양 = [n_class * (n_class-1) / 2, n_features] 이 속성은 선형 커널의 경우에만 사용할 수 있으며 기능에 할당 된 가중치를 제공합니다.
6	intercept_ − 배열, 모양 = [n_class * (n_class-1) / 2] 의사 결정 기능에서 독립적 인 용어 (상수)를 나타냅니다.
7	fit_status_ − 정수 올바르게 장착 된 경우 출력은 0이됩니다. 잘못 장착 된 경우 출력은 1이됩니다.
8	classes_ − 모양 배열 = [n_classes] 클래스의 레이블을 제공합니다.

Implementation Example

다른 분류기와 마찬가지로 SVC도 다음 두 배열에 적합해야합니다.

• 배열 X훈련 샘플을 들고. 크기는 [n_samples, n_features]입니다.

• 배열 Y목표 값, 즉 훈련 샘플에 대한 클래스 레이블을 보유합니다. 크기는 [n_samples]입니다.

다음 Python 스크립트 사용 sklearn.svm.SVC 클래스-

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)

Output

SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, probability = False, random_state = None, shrinking = False,
   tol = 0.001, verbose = False)

Example

이제 적합하면 다음 파이썬 스크립트의 도움으로 가중치 벡터를 얻을 수 있습니다.

SVCClf.coef_

Output

array([[0.5, 0.5]])

Example

마찬가지로 다음과 같이 다른 속성의 값을 얻을 수 있습니다.

SVCClf.predict([[-0.5,-0.8]])

Output

array([1])

Example

SVCClf.n_support_

Output

array([1, 1])

Example

SVCClf.support_vectors_

Output

array(
   [
      [-1., -1.],
      [ 1., 1.]
   ]
)

Example

SVCClf.support_

Output

array([0, 2])

Example

SVCClf.intercept_

Output

array([-0.])

Example

SVCClf.fit_status_

Output

0

NuSVC

NuSVC는 Nu 지원 벡터 분류입니다. 다중 클래스 분류를 수행 할 수있는 scikit-learn에서 제공하는 또 다른 클래스입니다. SVC와 비슷하지만 NuSVC는 약간 다른 매개 변수 집합을 허용합니다. SVC와 다른 매개 변수는 다음과 같습니다.

• nu − 부동, 선택, 기본값 = 0.5

훈련 오류 비율의 상한과 지원 벡터 비율의 하한을 나타냅니다. 값은 (o, 1] 간격에 있어야합니다.

나머지 매개 변수와 속성은 SVC와 동일합니다.

구현 예

다음을 사용하여 동일한 예제를 구현할 수 있습니다. sklearn.svm.NuSVC 수업도.

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)

산출

NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, nu = 0.5, probability = False, random_state = None,
   shrinking = False, tol = 0.001, verbose = False)

SVC의 경우처럼 나머지 속성의 출력을 얻을 수 있습니다.

LinearSVC

선형 지원 벡터 분류입니다. 커널 = 'linear'인 SVC와 유사합니다. 그들 사이의 차이점은LinearSVC liblinear 측면에서 구현되는 반면 SVC는 libsvm. 그게 이유야LinearSVC페널티 및 손실 기능을 더 유연하게 선택할 수 있습니다. 또한 많은 수의 샘플로 더 잘 확장됩니다.

매개 변수와 속성에 대해 이야기하면 지원하지 않습니다. ‘kernel’ 선형이라고 가정하고 다음과 같은 속성이 부족하기 때문입니다. support_, support_vectors_, n_support_, fit_status_ 과, dual_coef_.

그러나 그것은 지원합니다 penalty 과 loss 다음과 같이 매개 변수-

• penalty − string, L1 or L2(default = ‘L2’)

  이 매개 변수는 벌점 (정규화)에 사용되는 표준 (L1 또는 L2)을 지정하는 데 사용됩니다.

• loss − string, hinge, squared_hinge (default = squared_hinge)

  'hinge'가 표준 SVM 손실이고 'squared_hinge'가 힌지 손실의 제곱 인 손실 함수를 나타냅니다.

구현 예

다음 Python 스크립트 사용 sklearn.svm.LinearSVC 클래스-

from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)

산출

LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
   intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
   multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)

예

이제 적합하면 모델은 다음과 같이 새로운 값을 예측할 수 있습니다.

LSVCClf.predict([[0,0,0,0]])

산출

[1]

예

위의 예에서 다음 파이썬 스크립트를 사용하여 가중치 벡터를 얻을 수 있습니다.

LSVCClf.coef_

산출

[[0. 0. 0.91214955 0.22630686]]

예

유사하게, 우리는 다음 파이썬 스크립트의 도움으로 intercept의 값을 얻을 수 있습니다.

LSVCClf.intercept_

산출

[0.26860518]

SVM을 사용한 회귀

앞서 논의했듯이 SVM은 분류 및 회귀 문제 모두에 사용됩니다. Scikit-learn의 SVC (Support Vector Classification) 방법을 확장하여 회귀 문제를 해결할 수도 있습니다. 확장 된 방법을 SVR (Support Vector Regression)이라고합니다.

SVM과 SVR의 기본적인 유사성

SVC에서 생성 된 모델은 훈련 데이터의 하위 집합에만 의존합니다. 왜? 모델을 구축하기위한 비용 함수는 마진 밖에있는 훈련 데이터 포인트에 대해 신경 쓰지 않기 때문입니다.

반면 SVR (Support Vector Regression)에 의해 생성 된 모델은 훈련 데이터의 하위 집합에만 의존합니다. 왜? 모델 구축을위한 비용 함수는 모델 예측에 가까운 모든 학습 데이터 포인트를 무시하기 때문입니다.

Scikit-learn은 세 가지 클래스를 제공합니다. SVR, NuSVR and LinearSVR SVR의 세 가지 다른 구현으로.

SVR

구현이 기반으로하는 Epsilon 지원 벡터 회귀입니다. libsvm. 반대로SVC 모델에는 두 개의 자유 매개 변수가 있습니다. ‘C’ 과 ‘epsilon’.

• epsilon − 부동, 선택, 기본값 = 0.1

엡실론 -SVR 모델의 엡실론을 나타내며, 실제 값에서 거리 엡실론 내에서 예측 된 포인트로 훈련 손실 함수에서 페널티가없는 엡실론 튜브를 지정합니다.

나머지 매개 변수와 속성은 우리가 사용한 것과 유사합니다. SVC.

구현 예

다음 Python 스크립트 사용 sklearn.svm.SVR 클래스-

from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)

산출

SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
   kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)

예

이제 적합하면 다음 파이썬 스크립트의 도움으로 가중치 벡터를 얻을 수 있습니다.

SVRReg.coef_

산출

array([[0.4, 0.4]])

예

마찬가지로 다음과 같이 다른 속성의 값을 얻을 수 있습니다.

SVRReg.predict([[1,1]])

산출

array([1.1])

마찬가지로 다른 속성의 값도 얻을 수 있습니다.

NuSVR

NuSVR은 Nu 지원 벡터 회귀입니다. NuSVC와 비슷하지만 NuSVR은 매개 변수를 사용합니다.nu지원 벡터의 수를 제어합니다. 또한 NuSVC와 달리nu C 매개 변수를 대체했습니다. 여기서는 epsilon.

구현 예

다음 Python 스크립트 사용 sklearn.svm.SVR 클래스-

from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)

산출

NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
   kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
   verbose = False)

예

이제 적합하면 다음 파이썬 스크립트의 도움으로 가중치 벡터를 얻을 수 있습니다.

NuSVRReg.coef_

산출

array(
   [
      [-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
      0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
      -0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
   ]
)

마찬가지로 다른 속성의 값도 얻을 수 있습니다.

LinearSVR

선형 지원 벡터 회귀입니다. 커널 = 'linear'인 SVR과 유사합니다. 그들 사이의 차이점은LinearSVR 측면에서 구현 liblinear, SVC는 libsvm. 그게 이유야LinearSVR페널티 및 손실 기능을 더 유연하게 선택할 수 있습니다. 또한 많은 수의 샘플로 더 잘 확장됩니다.

매개 변수와 속성에 대해 이야기하면 지원하지 않습니다. ‘kernel’ 선형이라고 가정하고 다음과 같은 속성이 부족하기 때문입니다. support_, support_vectors_, n_support_, fit_status_ 과, dual_coef_.

그러나 다음과 같이 '손실'매개 변수를 지원합니다.

• loss − 문자열, 선택 사항, 기본값 = 'epsilon_insensitive'

epsilon_insensitive loss가 L1 손실이고 제곱 된 epsilon-insensitive loss가 L2 손실 인 손실 함수를 나타냅니다.

구현 예

다음 Python 스크립트 사용 sklearn.svm.LinearSVR 클래스-

from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)

산출

LinearSVR(
   C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
   intercept_scaling=1.0, loss='squared_epsilon_insensitive',
   max_iter=1000, random_state=0, tol=1e-05, verbose=0
)

예

이제 적합하면 모델은 다음과 같이 새로운 값을 예측할 수 있습니다.

LSRReg.predict([[0,0,0,0]])

산출

array([-0.01041416])

예

위의 예에서 다음 파이썬 스크립트를 사용하여 가중치 벡터를 얻을 수 있습니다.

LSRReg.coef_

산출

array([20.47354746, 34.08619401, 67.23189022, 87.47017787])

예

유사하게, 우리는 다음 파이썬 스크립트의 도움으로 intercept의 값을 얻을 수 있습니다.

LSRReg.intercept_

산출

array([-0.01041416])

여기에서는 Sklearn에서 이상 감지가 무엇인지, 데이터 포인트 식별에 어떻게 사용되는지에 대해 알아 봅니다.

이상 탐지는 나머지 데이터와 잘 맞지 않는 데이터 세트의 데이터 포인트를 식별하는 데 사용되는 기술입니다. 사기 탐지, 침입 탐지, 시스템 상태 모니터링, 감시 및 예측 유지 관리와 같은 비즈니스에 많은 응용 프로그램이 있습니다. 이상치라고도하는 이상 치는 다음 세 가지 범주로 나눌 수 있습니다.

• Point anomalies − 개별 데이터 인스턴스가 나머지 데이터에 대해 비정상적인 것으로 간주 될 때 발생합니다.

• Contextual anomalies− 이러한 종류의 이상은 상황에 따라 다릅니다. 데이터 인스턴스가 특정 컨텍스트에서 비정상적인 경우 발생합니다.

• Collective anomalies − 관련 데이터 인스턴스 모음이 개별 값이 아닌 전체 데이터 세트에서 비정상적인 경우 발생합니다.

행동 양식

즉 두 가지 방법 outlier detection 과 novelty detection이상 탐지에 사용할 수 있습니다. 그들 사이의 차이를 볼 필요가 있습니다.

이상치 감지

훈련 데이터에는 나머지 데이터와는 거리가 먼 이상 치가 포함됩니다. 이러한 이상 치는 관측치로 정의됩니다. 그렇기 때문에 이상치 탐지 추정자는 항상 비정상적인 관찰을 무시하면서 가장 집중된 훈련 데이터가있는 영역을 맞추려고합니다. 비지도 이상 탐지라고도합니다.

참신 감지

훈련 데이터에 포함되지 않은 새로운 관찰에서 관찰되지 않은 패턴을 탐지하는 것과 관련이 있습니다. 여기서 훈련 데이터는 특이 치에 의해 오염되지 않습니다. 반 감독 이상 탐지라고도합니다.

scikit-learn에서 제공하는 ML 도구 세트가 있으며, 이는 이상치 감지와 신규성 감지 모두에 사용할 수 있습니다. 이 도구는 먼저 다음과 같이 fit () 방법을 사용하여 감독되지 않은 데이터에서 객체 학습을 구현합니다.

estimator.fit(X_train)

이제 새 관측 값은 다음과 같이 정렬됩니다. inliers (labeled 1) 또는 outliers (labeled -1) 다음과 같이 predict () 메서드를 사용하여-

estimator.fit(X_test)

추정기는 먼저 원시 스코어링 함수를 계산 한 다음 예측 방법이 해당 원시 스코어링 함수의 임계 값을 사용합니다. 이 원시 채점 기능에 액세스 할 수 있습니다.score_sample 방법으로 임계 값을 제어 할 수 있습니다. contamination 매개 변수.

우리는 또한 정의 할 수 있습니다 decision_function 이상 값을 음수 값으로, 내부 값을 음수가 아닌 값으로 정의하는 방법입니다.

estimator.decision_function(X_test)

이상치 탐지를위한 Sklearn 알고리즘

타원 봉투가 무엇인지 이해하는 것으로 시작하겠습니다.

타원 봉투 맞추기

이 알고리즘은 정규 데이터가 가우스 분포와 같은 알려진 분포에서 나온다고 가정합니다. 이상 값 감지를 위해 Scikit-learn은covariance.EllipticEnvelop.

이 객체는 로버 스트 공분산 추정치를 데이터에 맞추므로 타원을 중앙 데이터 포인트에 맞 춥니 다. 중앙 모드 외부의 점은 무시합니다.

매개 변수

다음 표는 sklearn. covariance.EllipticEnvelop 방법-

Sr. 아니요	매개 변수 및 설명
1	store_precision − 부울, 옵션, 기본값 = True 추정 된 정밀도가 저장되면이를 지정할 수 있습니다.
2	assume_centered − 부울, 옵션, 기본값 = False False로 설정하면 FastMCD 알고리즘을 사용하여 강력한 위치와 공분산을 직접 계산합니다. 반면에 True로 설정하면 강력한 위치 및 covarian의 지원을 계산합니다.
삼	support_fraction − 부동 (0., 1), 옵션, 기본값 = 없음 이 매개 변수는 원시 MCD 추정의 지원에 포함될 포인트의 비율을 방법에 알려줍니다.
4	contamination − 부동 (0., 1.), 선택 사항, 기본값 = 0.1 데이터 세트에서 이상 값의 비율을 제공합니다.
5	random_state − int, RandomState 인스턴스 또는 None, 선택 사항, 기본값 = 없음 이 매개 변수는 데이터를 섞는 동안 사용되는 생성 된 의사 난수의 시드를 나타냅니다. 다음은 옵션입니다- int −이 경우 random_state 난수 생성기에서 사용하는 시드입니다. RandomState instance−이 경우 random_state 는 난수 생성기입니다. None −이 경우 난수 생성기는 np.random에서 사용하는 RandonState 인스턴스입니다.

속성

다음 표는 sklearn. covariance.EllipticEnvelop 방법-

Sr. 아니요	속성 및 설명
1	support_ − 배열 형, 모양 (n_samples,) 위치와 모양에 대한 강력한 추정치를 계산하는 데 사용되는 관찰의 마스크를 나타냅니다.
2	location_ − 배열 형, 모양 (n_features) 추정 된 견고한 위치를 반환합니다.
삼	covariance_ − 배열 형, 모양 (n_features, n_features) 추정 된 로버 스트 공분산 행렬을 반환합니다.
4	precision_ − 배열 형, 모양 (n_features, n_features) 추정 된 의사 역행렬을 반환합니다.
5	offset_ − 플로트 원시 점수에서 결정 기능을 정의하는 데 사용됩니다. decision_function = score_samples -offset_

Implementation Example

import numpy as np^M
from sklearn.covariance import EllipticEnvelope^M
true_cov = np.array([[.5, .6],[.6, .4]])
X = np.random.RandomState(0).multivariate_normal(mean = [0, 0], cov=true_cov,size=500)
cov = EllipticEnvelope(random_state = 0).fit(X)^M
# Now we can use predict method. It will return 1 for an inlier and -1 for an outlier.
cov.predict([[0, 0],[2, 2]])

Output

array([ 1, -1])

고립의 숲

고차원 데이터 세트의 경우 이상 값 감지를위한 효율적인 방법 중 하나는 랜덤 포레스트를 사용하는 것입니다. scikit-learn은ensemble.IsolationForest특징을 무작위로 선택하여 관찰을 분리하는 방법. 그 후 선택된 피처의 최대 값과 최소값 사이의 값을 무작위로 선택합니다.

여기서 샘플을 분리하는 데 필요한 분할 횟수는 루트 노드에서 종료 노드까지의 경로 길이와 같습니다.

매개 변수

다음 표는 sklearn. ensemble.IsolationForest 방법-

Sr. 아니요	매개 변수 및 설명
1	n_estimators − int, 선택, 기본값 = 100 앙상블의 기본 추정자 수를 나타냅니다.
2	max_samples − int 또는 float, 선택 사항, 기본값 = "auto" 각 기본 추정기를 훈련하기 위해 X에서 추출 할 샘플 수를 나타냅니다. 값으로 int를 선택하면 max_samples 샘플을 그립니다. 값으로 float를 선택하면 max_samples ∗ .shape [0] 샘플을 그립니다. 그리고 auto를 값으로 선택하면 max_samples = min (256, n_samples)이 그려집니다.
삼	support_fraction − 부동 (0., 1), 옵션, 기본값 = 없음 이 매개 변수는 원시 MCD 추정의 지원에 포함될 포인트의 비율을 방법에 알려줍니다.
4	contamination − auto 또는 float, 선택 사항, 기본값 = auto 데이터 세트에서 이상 값의 비율을 제공합니다. 기본값, 즉 자동으로 설정하면 원본 용지에서와 같이 임계 값이 결정됩니다. float로 설정하면 오염 범위는 [0,0.5] 범위가됩니다.
5	random_state − int, RandomState 인스턴스 또는 None, 선택 사항, 기본값 = 없음 이 매개 변수는 데이터를 섞는 동안 사용되는 생성 된 의사 난수의 시드를 나타냅니다. 다음은 옵션입니다- int −이 경우 random_state 난수 생성기에서 사용하는 시드입니다. RandomState instance−이 경우 random_state 는 난수 생성기입니다. None −이 경우 난수 생성기는 np.random에서 사용하는 RandonState 인스턴스입니다.
6	max_features − int 또는 float, 선택 사항 (기본값 = 1.0) 각 기본 추정기를 훈련하기 위해 X에서 추출 할 특성의 수를 나타냅니다. 값으로 int를 선택하면 max_features 기능을 그립니다. 값으로 float를 선택하면 max_features * X.shape [] 샘플을 그립니다.
7	bootstrap − 부울, 선택 사항 (기본값 = False) 기본 옵션은 False로 대체하지 않고 샘플링을 수행합니다. 반면 True로 설정하면 개별 트리가 대체로 샘플링 된 훈련 데이터의 무작위 하위 집합에 적합 함을 의미합니다.
8	n_jobs − int 또는 None, 선택 사항 (기본값 = None) 병렬로 실행할 작업 수를 나타냅니다. fit() 과 predict() 방법 둘 다.
9	verbose − int, 선택 사항 (기본값 = 0) 이 매개 변수는 트리 작성 프로세스의 자세한 정도를 제어합니다.
10	warm_start − Bool, 선택 사항 (기본값 = False) warm_start = true이면 이전 호출 솔루션을 다시 사용할 수 있으며 앙상블에 더 많은 추정기를 추가 할 수 있습니다. 하지만 false로 설정되면 완전히 새로운 포리스트를 맞아야합니다.

속성

다음 표는 sklearn. ensemble.IsolationForest 방법-

Sr. 아니요	속성 및 설명
1	estimators_ − DecisionTreeClassifier 목록 모든 피팅 된 하위 추정기의 수집을 제공합니다.
2	max_samples_ − 정수 사용 된 실제 샘플 수를 제공합니다.
삼	offset_ − 플로트 원시 점수에서 결정 기능을 정의하는 데 사용됩니다. decision_function = score_samples -offset_

Implementation Example

아래 Python 스크립트는 sklearn. ensemble.IsolationForest 주어진 데이터에 10 개의 나무를 맞추는 방법

from sklearn.ensemble import IsolationForest
import numpy as np
X = np.array([[-1, -2], [-3, -3], [-3, -4], [0, 0], [-50, 60]])
OUTDClf = IsolationForest(n_estimators = 10)
OUTDclf.fit(X)

Output

IsolationForest(
   behaviour = 'old', bootstrap = False, contamination='legacy',
   max_features = 1.0, max_samples = 'auto', n_estimators = 10, n_jobs=None,
   random_state = None, verbose = 0
)

국부 이상치 요인

LOF (Local Outlier Factor) 알고리즘은 고차원 데이터에서 이상 값 감지를 수행하는 또 다른 효율적인 알고리즘입니다. scikit-learn은neighbors.LocalOutlierFactor관측치의 비정상 성 정도를 반영하는 로컬 이상치 요인이라는 점수를 계산하는 방법입니다. 이 알고리즘의 주요 논리는 이웃보다 밀도가 상당히 낮은 샘플을 감지하는 것입니다. 그렇기 때문에 주어진 데이터 포인트의 로컬 밀도 편차를 이웃과 측정합니다.

매개 변수

다음 표는 sklearn. neighbors.LocalOutlierFactor 방법

Sr. 아니요	매개 변수 및 설명
1	n_neighbors − int, 선택, 기본값 = 20 kneighbors 쿼리에 기본적으로 사용하는 이웃 수를 나타냅니다. 모든 샘플은.
2	algorithm − 선택 사항 최근 접 이웃 계산에 사용할 알고리즘입니다. ball_tree를 선택하면 BallTree 알고리즘을 사용합니다. kd_tree를 선택하면 KDTree 알고리즘을 사용합니다. 무차별 대입을 선택하면 무차별 대입 검색 알고리즘을 사용합니다. auto를 선택하면 fit () 메서드에 전달한 값을 기반으로 가장 적합한 알고리즘을 결정합니다.
삼	leaf_size − int, 선택, 기본값 = 30 이 매개 변수의 값은 구성 및 쿼리 속도에 영향을 줄 수 있습니다. 또한 트리를 저장하는 데 필요한 메모리에도 영향을줍니다. 이 매개 변수는 BallTree 또는 KdTree 알고리즘에 전달됩니다.
4	contamination − auto 또는 float, 선택 사항, 기본값 = auto 데이터 세트에서 이상 값의 비율을 제공합니다. 기본값, 즉 자동으로 설정하면 원본 용지에서와 같이 임계 값이 결정됩니다. float로 설정하면 오염 범위는 [0,0.5] 범위가됩니다.
5	metric − 문자열 또는 호출 가능, 기본값 거리 계산에 사용되는 메트릭을 나타냅니다.
6	P − int, 선택 사항 (기본값 = 2) Minkowski 메트릭의 매개 변수입니다. P = 1은 manhattan_distance 즉 L1을 사용하는 것과 같고 P = 2는 euclidean_distance 즉 L2를 사용하는 것과 같습니다.
7	novelty − 부울, (기본값 = False) 기본적으로 LOF 알고리즘은 이상치 감지에 사용되지만 novelty = true로 설정하면 신규성 감지에 사용할 수 있습니다.
8	n_jobs − int 또는 None, 선택 사항 (기본값 = None) fit () 및 predict () 메서드 모두에 대해 병렬로 실행할 작업 수를 나타냅니다.

속성

다음 표는 sklearn.neighbors.LocalOutlierFactor 방법-

Sr. 아니요	속성 및 설명
1	negative_outlier_factor_ − numpy 배열, 모양 (n_samples,) 훈련 샘플의 반대 LOF를 제공합니다.
2	n_neighbors_ − 정수 이웃 쿼리에 사용되는 실제 이웃 수를 제공합니다.
삼	offset_ − 플로트 원시 점수에서 이진 레이블을 정의하는 데 사용됩니다.

Implementation Example

아래 주어진 Python 스크립트는 sklearn.neighbors.LocalOutlierFactor 데이터 세트에 해당하는 배열에서 NeighborsClassifier 클래스를 생성하는 메서드

from sklearn.neighbors import NearestNeighbors
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
LOFneigh = NearestNeighbors(n_neighbors = 1, algorithm = "ball_tree",p=1)
LOFneigh.fit(samples)

Output

NearestNeighbors(
   algorithm = 'ball_tree', leaf_size = 30, metric='minkowski',
   metric_params = None, n_jobs = None, n_neighbors = 1, p = 1, radius = 1.0
)

Example

이제 다음 파이썬 스크립트를 사용하여이 구성된 분류 자에서 [0.5, 1., 1.5]에 대한 옷장 지점을 물어볼 수 있습니다.

print(neigh.kneighbors([[.5, 1., 1.5]])

Output

(array([[1.7]]), array([[1]], dtype = int64))

단일 클래스 SVM

Schölkopf 등이 소개 한 One-Class SVM은 감독되지 않은 이상치 탐지입니다. 또한 고차원 데이터에서 매우 효율적이며 고차원 분포의 지원을 추정합니다. 그것은에서 구현됩니다Support Vector Machines 모듈 Sklearn.svm.OneClassSVM목적. 프론티어를 정의하려면 커널 (주로 사용되는 것은 RBF)과 스칼라 매개 변수가 필요합니다.

더 나은 이해를 위해 데이터를 svm.OneClassSVM 객체-

예

from sklearn.svm import OneClassSVM
X = [[0], [0.89], [0.90], [0.91], [1]]
OSVMclf = OneClassSVM(gamma = 'scale').fit(X)

이제 다음과 같이 입력 데이터에 대한 score_samples를 얻을 수 있습니다.

OSVMclf.score_samples(X)

산출

array([1.12218594, 1.58645126, 1.58673086, 1.58645127, 1.55713767])

이 장은 Sklearn에서 가장 가까운 이웃 방법을 이해하는 데 도움이 될 것입니다.

이웃 기반 학습 방법은 두 가지 유형입니다. supervised 과 unsupervised. 지도 이웃 기반 학습은 분류 및 회귀 예측 문제 모두에 사용할 수 있지만 주로 산업의 분류 예측 문제에 사용됩니다.

이웃 기반 학습 방법에는 특수 훈련 단계가 없으며 분류하는 동안 모든 데이터를 훈련에 사용합니다. 또한 기본 데이터에 대해 아무것도 가정하지 않습니다. 이것이 그들이 본질적으로 게으르고 매개 변수가 아닌 이유입니다.

최근 접 이웃 방법의 기본 원리는 다음과 같습니다.

• 새 데이터 포인트와 거리가 먼 사전 정의 된 수의 훈련 샘플 옷장을 찾으려면

• 이러한 수의 훈련 샘플에서 레이블을 예측합니다.

여기서 샘플 수는 K- 최근 접 이웃 학습과 같이 사용자 정의 상수이거나 반경 기반 이웃 학습과 같이 점의 국소 밀도에 따라 달라질 수 있습니다.

sklearn.neighbors 모듈

Scikit-learn은 sklearn.neighbors비지도 및지도 이웃 기반 학습 방법 모두에 대한 기능을 제공하는 모듈입니다. 입력으로이 모듈의 클래스는 NumPy 배열 또는scipy.sparse 행렬.

알고리즘 유형

이웃 기반 방법의 구현에서 사용할 수있는 다양한 유형의 알고리즘은 다음과 같습니다.

무차별 대입

데이터 세트의 모든 포인트 쌍 사이의 거리를 무차별 대입하여 계산하면 가장 순진한 인접 검색 구현을 제공합니다. 수학적으로 D 차원의 N 개 샘플에 대해 무차별 대입 접근 방식은 다음과 같이 확장됩니다.0[DN²]

작은 데이터 샘플의 경우이 알고리즘은 매우 유용 할 수 있지만 샘플 수가 증가하면 실행 불가능 해집니다. 무차별 대입 이웃 검색은 키워드를 작성하여 활성화 할 수 있습니다.algorithm=’brute’.

KD 트리

무차별 대입 방식의 계산 비 효율성을 해결하기 위해 고안된 트리 기반 데이터 구조 중 하나는 KD 트리 데이터 구조입니다. 기본적으로 KD 트리는 K 차원 트리라고하는 이진 트리 구조입니다. 데이터 포인트가 채워지는 중첩 된 직교 영역으로 분할하여 데이터 축을 따라 매개 변수 공간을 재귀 적으로 분할합니다.

장점

다음은 KD 트리 알고리즘의 몇 가지 장점입니다.

Construction is fast − 파티셔닝이 데이터 축을 따라서 만 수행되므로 KD 트리의 구성이 매우 빠릅니다.

Less distance computations−이 알고리즘은 쿼리 포인트의 가장 가까운 이웃을 결정하는 데 매우 적은 거리 계산을 사용합니다. 소요됩니다[ ()] 거리 계산.

단점

Fast for only low-dimensional neighbor searches− 저 차원 (D <20) 이웃 검색의 경우 매우 빠르지 만 D가 증가하면 비효율적입니다. 파티셔닝은 데이터 축을 따라서 만 수행되므로

KD 트리 이웃 검색은 키워드를 작성하여 활성화 할 수 있습니다. algorithm=’kd_tree’.

볼 트리

KD Tree는 고차원에서 비효율적이라는 것을 알고 있으므로 KD Tree의 비 효율성을 해결하기 위해 Ball tree 데이터 구조를 개발했습니다. 수학적으로는 데이터를 중심 C와 반경 r로 정의 된 노드로 재귀 적으로 나눕니다. 즉, 노드의 각 점이 중심으로 정의 된 하이퍼 스피어 내에 있습니다.C 및 반경 r. 아래에 주어진 삼각형 부등식을 사용하여 인접 검색에 대한 후보 포인트 수를 줄입니다.

$$\arrowvert X+Y\arrowvert\leq \arrowvert X\arrowvert+\arrowvert Y\arrowvert$$

장점

다음은 볼 트리 알고리즘의 몇 가지 장점입니다.

Efficient on highly structured data − 볼 트리가 일련의 중첩 하이퍼 스피어로 데이터를 분할하므로 고도로 구조화 된 데이터에 효율적입니다.

Out-performs KD-tree − 볼 트리는 볼 트리 노드의 구형 기하학을 가지고 있기 때문에 높은 차원에서 KD 트리보다 성능이 뛰어납니다.

단점

Costly − 데이터를 일련의 중첩 하이퍼 스피어로 분할하면 구성 비용이 매우 많이 듭니다.

키워드를 작성하여 볼 트리 이웃 검색을 활성화 할 수 있습니다. algorithm=’ball_tree’.

최근 접 이웃 알고리즘 선택

주어진 데이터 세트에 대한 최적의 알고리즘 선택은 다음 요인에 따라 달라집니다.

샘플 수 (N) 및 차원 (D)

Nearest Neighbor 알고리즘을 선택할 때 고려해야 할 가장 중요한 요소입니다. 아래에 주어진 이유 때문입니다-

• Brute Force 알고리즘의 쿼리 시간은 O [DN]으로 증가합니다.

• Ball tree 알고리즘의 질의 시간은 O [D log (N)]만큼 증가합니다.

• KD 트리 알고리즘의 쿼리 시간은 특성화하기 매우 어려운 이상한 방식으로 D와 함께 변경됩니다. D <20 일 때 비용은 O [D log (N)]이고이 알고리즘은 매우 효율적입니다. 반면에 D> 20 인 경우 비용이 거의 O [DN]으로 증가하므로 비효율적입니다.

데이터 구조

이러한 알고리즘의 성능에 영향을 미치는 또 다른 요인은 데이터의 고유 차원 또는 데이터의 희소성입니다. Ball tree와 KD tree 알고리즘의 질의 시간이 크게 영향을받을 수 있기 때문입니다. 반면, Brute Force 알고리즘의 쿼리 시간은 데이터 구조에 의해 변경되지 않습니다. 일반적으로 볼 트리 및 KD 트리 알고리즘은 고유 차원이 더 작은 희소 데이터에 이식 될 때 더 빠른 쿼리 시간을 생성합니다.

이웃 수 (k)

쿼리 포인트에 대해 요청 된 이웃 수 (k)는 볼 트리 및 KD 트리 알고리즘의 쿼리 시간에 영향을줍니다. 이웃 수 (k)가 증가하면 쿼리 시간이 느려집니다. Brute Force의 쿼리 시간은 k 값의 영향을받지 않습니다.

쿼리 포인트 수

구성 단계가 필요하기 때문에 쿼리 포인트가 많은 경우 KD 트리 및 볼 트리 알고리즘이 모두 효과적입니다. 반면에 쿼리 포인트 수가 적 으면 Brute Force 알고리즘이 KD 트리 및 볼 트리 알고리즘보다 성능이 좋습니다.

가장 간단한 기계 학습 알고리즘 중 하나 인 k-NN (k-Nearest Neighbor)은 본질적으로 비모수 적이며 게으른 것입니다. 비모수는 기본 데이터 분포에 대한 가정이 없음을 의미합니다. 즉, 모델 구조가 데이터 세트에서 결정됩니다. 지연 또는 인스턴스 기반 학습은 모델 생성을 위해 학습 데이터 포인트가 필요하지 않으며 전체 학습 데이터가 테스트 단계에서 사용됨을 의미합니다.

k-NN 알고리즘은 다음 두 단계로 구성됩니다.

1 단계

이 단계에서는 훈련 세트의 각 샘플에 대해 k 개의 가장 가까운 이웃을 계산하고 저장합니다.

2 단계

이 단계에서는 라벨이없는 샘플의 경우 데이터 세트에서 k 개의 가장 가까운 이웃을 검색합니다. 그런 다음 이러한 k- 최근 접 이웃 중에서 투표를 통해 클래스를 예측합니다 (과반수 투표가이기는 클래스).

모듈, sklearn.neighbors k- 최근 접 이웃 알고리즘을 구현하고 다음 기능을 제공합니다. unsupervised 만큼 잘 supervised 이웃 기반 학습 방법.

감독되지 않은 가장 가까운 이웃은 각 샘플에 대한 가장 가까운 이웃을 찾기 위해 다른 알고리즘 (BallTree, KDTree 또는 Brute Force)을 구현합니다. 이 비지도 버전은 기본적으로 위에서 논의한 1 단계에 불과하며 이웃 검색을 필요로하는 많은 알고리즘 (KNN 및 K- 평균이 유명한 것임)의 기초입니다. 간단히 말해서 이웃 검색을 구현하는 비지도 학습자입니다.

한편, 감독 이웃 기반 학습은 회귀뿐만 아니라 분류에도 사용됩니다.

비지도 KNN 학습

논의한 바와 같이 최근 접 이웃 검색을 필요로하는 KNN 및 K-Means와 같은 많은 알고리즘이 있습니다. 이것이 바로 Scikit-learn이 이웃 검색 부분을 자체 "학습자"로 구현하기로 결정한 이유입니다. 이웃 검색을 별도의 학습자로 만드는 이유는 가장 가까운 이웃을 찾기 위해 모든 쌍별 거리를 계산하는 것이 분명히 효율적이지 않기 때문입니다. Sklearn에서 비지도 최근 접 이웃 학습을 구현하는 데 사용하는 모듈을 예제와 함께 살펴 보겠습니다.

Scikit-learn 모듈

sklearn.neighbors.NearestNeighbors감독되지 않은 최근 접 이웃 학습을 구현하는 데 사용되는 모듈입니다. BallTree, KDTree 또는 Brute Force라는 특정 최근 접 이웃 알고리즘을 사용합니다. 즉,이 세 가지 알고리즘에 대한 균일 한 인터페이스 역할을합니다.

매개 변수

다음 표는 NearestNeighbors 모듈-

Sr. 아니요	매개 변수 및 설명
1	n_neighbors − int, 선택 사항 얻을 이웃의 수. 기본값은 5입니다.
2	radius − 부동, 선택 사항 반환 할 이웃의 거리를 제한합니다. 기본값은 1.0입니다.
삼	algorithm − { 'auto', 'ball_tree', 'kd_tree', 'brute'}, 선택 사항 이 매개 변수는 가장 가까운 이웃을 계산하는 데 사용할 알고리즘 (BallTree, KDTree 또는 Brute-force)을 사용합니다. 'auto'를 제공하면 fit 메서드에 전달 된 값을 기반으로 가장 적합한 알고리즘을 결정합니다.
4	leaf_size − int, 선택 사항 트리를 저장하는 데 필요한 메모리뿐만 아니라 구성 및 쿼리 속도에 영향을 미칠 수 있습니다. BallTree 또는 KDTree로 전달됩니다. 최적의 값은 문제의 특성에 따라 다르지만 기본값은 30입니다.
5	metric − 문자열 또는 호출 가능 포인트 간 거리 계산에 사용하는 메트릭입니다. 문자열이나 호출 가능한 함수로 전달할 수 있습니다. 호출 가능한 함수의 경우 각 행 쌍에서 메트릭이 호출되고 결과 값이 기록됩니다. 메트릭 이름을 문자열로 전달하는 것보다 덜 효율적입니다. scikit-learn 또는 scipy.spatial.distance에서 측정 항목을 선택할 수 있습니다. 유효한 값은 다음과 같습니다. Scikit-learn − [ 'cosine', 'manhattan', 'Euclidean', 'l1', 'l2', 'cityblock'] Scipy.spatial.distance − [ 'braycurtis', 'canberra', 'chebyshev', 'dice', 'hamming', 'jaccard', 'correlation', 'kulsinski', 'mahalanobis', 'minkowski', 'rogerstanimoto', 'russellrao', ' sokalmicheme ','sokalsneath ','seuclidean ','sqeuclidean ','yule ']. 기본 측정 항목은 '민 코스키'입니다.
6	P − 정수, 선택 사항 Minkowski 메트릭의 매개 변수입니다. 기본값은 2이며 Euclidean_distance (l2)를 사용하는 것과 같습니다.
7	metric_params − dict, 선택 사항 메트릭 함수에 대한 추가 키워드 인수입니다. 기본값은 없음입니다.
8	N_jobs − int 또는 None, 선택 사항 이웃 검색을 위해 실행할 병렬 작업의 수를 재현합니다. 기본값은 없음입니다.

Implementation Example

아래 예제는 다음을 사용하여 두 데이터 세트 사이의 가장 가까운 이웃을 찾습니다 sklearn.neighbors.NearestNeighbors 기준 치수.

먼저 필요한 모듈과 패키지를 가져와야합니다.

from sklearn.neighbors import NearestNeighbors
import numpy as np

이제 패키지를 가져온 후 가장 가까운 이웃을 찾고자하는 사이의 데이터 세트를 정의합니다.

Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])

다음으로, 다음과 같이 비지도 학습 알고리즘을 적용하십시오.

nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm = 'ball_tree')

다음으로 입력 데이터 세트로 모델을 피팅합니다.

nrst_neigh.fit(Input_data)

이제 데이터 세트의 K- 이웃을 찾으십시오. 각 포인트의 이웃 인덱스와 거리를 반환합니다.

distances, indices = nbrs.kneighbors(Input_data)
indices

Output

array(
   [
      [0, 1, 3],
      [1, 2, 0],
      [2, 1, 0],
      [3, 4, 0],
      [4, 5, 3],
      [5, 6, 4],
      [6, 5, 4]
   ], dtype = int64
)
distances

Output

array(
   [
      [0. , 1.41421356, 2.23606798],
      [0. , 1.41421356, 1.41421356],
      [0. , 1.41421356, 2.82842712],
      [0. , 1.41421356, 2.23606798],
      [0. , 1.41421356, 1.41421356],
      [0. , 1.41421356, 1.41421356],
      [0. , 1.41421356, 2.82842712]
   ]
)

위의 출력은 각 점의 가장 가까운 이웃이 점 자체, 즉 0임을 보여줍니다. 쿼리 세트가 훈련 세트와 일치하기 때문입니다.

Example

다음과 같이 희소 그래프를 생성하여 인접 지점 간의 연결을 표시 할 수도 있습니다.

nrst_neigh.kneighbors_graph(Input_data).toarray()

Output

array(
   [
      [1., 1., 0., 1., 0., 0., 0.],
      [1., 1., 1., 0., 0., 0., 0.],
      [1., 1., 1., 0., 0., 0., 0.],
      [1., 0., 0., 1., 1., 0., 0.],
      [0., 0., 0., 1., 1., 1., 0.],
      [0., 0., 0., 0., 1., 1., 1.],
      [0., 0., 0., 0., 1., 1., 1.]
   ]
)

감독되지 않은 사람에게 적합하면 NearestNeighbors 모델의 경우 데이터는 인수에 대해 설정된 값을 기반으로 데이터 구조에 저장됩니다. ‘algorithm’. 그 후이 비지도 학습자의kneighbors 이웃 검색이 필요한 모델에서.

Complete working/executable program

from sklearn.neighbors import NearestNeighbors
import numpy as np
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm='ball_tree')
nrst_neigh.fit(Input_data)
distances, indices = nbrs.kneighbors(Input_data)
indices
distances
nrst_neigh.kneighbors_graph(Input_data).toarray()

감독 된 KNN 학습

지도 이웃 기반 학습은 다음에 사용됩니다-

• 분류, 개별 레이블이있는 데이터
• 연속 레이블이있는 데이터에 대한 회귀.

최근 접 이웃 분류기

다음 두 가지 특성을 통해 이웃 기반 분류를 이해할 수 있습니다.

• 각 포인트의 가장 가까운 이웃에 대한 단순 다수결로 계산됩니다.
• 그것은 단순히 훈련 데이터의 인스턴스를 저장하기 때문에 비 일반화 학습 유형입니다.

Scikit-learn 모듈

다음은 scikit-learn에서 사용하는 두 가지 유형의 가장 가까운 이웃 분류기입니다.

S. 아니.	분류기 및 설명
1.	KNeighborsClassifier 이 분류기 이름의 K는 k 개의 가장 가까운 이웃을 나타냅니다. 여기서 k는 사용자가 지정한 정수 값입니다. 따라서 이름에서 알 수 있듯이이 분류기는 k 개의 최근 접 이웃을 기반으로 학습을 구현합니다. k 값의 선택은 데이터에 따라 다릅니다.
2.	RadiusNeighborsClassifier 이 분류기 이름의 반경은 지정된 반경 r 내에서 가장 가까운 이웃을 나타냅니다. 여기서 r은 사용자가 지정한 부동 소수점 값입니다. 따라서 이름에서 알 수 있듯이이 분류기는 각 훈련 포인트의 고정 반경 r 내의 이웃 수를 기반으로 학습을 구현합니다.

최근 접 이웃 회귀 분석기

데이터 레이블이 본질적으로 연속적인 경우에 사용됩니다. 할당 된 데이터 레이블은 가장 가까운 이웃 레이블의 평균을 기반으로 계산됩니다.

다음은 scikit-learn에서 사용하는 두 가지 유형의 가장 가까운 이웃 회귀 분석입니다.

KNeighborsRegressor

이 회귀 변수 이름의 K는 k 개의 가장 가까운 이웃을 나타냅니다. 여기서 k 이다 integer value사용자가 지정합니다. 따라서 이름에서 알 수 있듯이이 회귀 분석기는 k 개의 최근 접 이웃을 기반으로 학습을 구현합니다. k 값의 선택은 데이터에 따라 다릅니다. 구현 예를 통해 더 자세히 이해해 봅시다.

다음은 scikit-learn에서 사용하는 두 가지 유형의 가장 가까운 이웃 회귀 분석입니다.

구현 예

이 예에서는 scikit-learn을 사용하여 Iris Flower 데이터 세트라는 데이터 세트에 KNN을 구현합니다. KNeighborsRegressor.

먼저 다음과 같이 홍채 데이터 세트를 가져옵니다.

from sklearn.datasets import load_iris
iris = load_iris()

이제 데이터를 훈련 및 테스트 데이터로 분할해야합니다. Sklearn을 사용할 것입니다.train_test_split 70 (훈련 데이터)과 20 (테스트 데이터)의 비율로 데이터를 분할하는 기능-

X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)

다음으로 Sklearn 전처리 모듈의 도움으로 다음과 같이 데이터 스케일링을 수행합니다.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

다음으로 KNeighborsRegressor Sklearn에서 클래스를 만들고 다음과 같이 이웃 값을 제공하십시오.

예

import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 8)
knnr.fit(X_train, y_train)

산출

KNeighborsRegressor(
   algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
   metric_params = None, n_jobs = None, n_neighbors = 8, p = 2,
   weights = 'uniform'
)

예

이제 다음과 같이 MSE (평균 제곱 오차)를 찾을 수 있습니다.

print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))

산출

The MSE is: 4.4333349609375

예

이제 다음과 같이 값을 예측하는 데 사용하십시오.

X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))

산출

[0.66666667]

완전한 작업 / 실행 가능 프로그램

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()

scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=8)
knnr.fit(X_train, y_train)

print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))

X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))

RadiusNeighborsRegressor

이 회귀 분석기 이름의 반경은 지정된 반경 r 내에서 가장 가까운 이웃을 나타냅니다. 여기서 r은 사용자가 지정한 부동 소수점 값입니다. 따라서 이름에서 알 수 있듯이이 회귀 분석기는 각 훈련 포인트의 고정 반경 r 내의 이웃 수를 기반으로 학습을 구현합니다. 구현 예가 있으면 도움을 받아 더 많이 이해합시다.

구현 예

이 예에서는 scikit-learn을 사용하여 Iris Flower 데이터 세트라는 데이터 세트에 KNN을 구현합니다. RadiusNeighborsRegressor −

먼저 다음과 같이 홍채 데이터 세트를 가져옵니다.

from sklearn.datasets import load_iris
iris = load_iris()

이제 데이터를 훈련 및 테스트 데이터로 분할해야합니다. Sklearn train_test_split 함수를 사용하여 데이터를 70 (훈련 데이터)과 20 (테스트 데이터)의 비율로 분할합니다.

X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)

다음으로 Sklearn 전처리 모듈의 도움으로 다음과 같이 데이터 스케일링을 수행합니다.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

다음으로 RadiusneighborsRegressor Sklearn에서 클래스를 만들고 다음과 같이 반경 값을 제공하십시오-

import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X_train, y_train)

예

이제 다음과 같이 MSE (평균 제곱 오차)를 찾을 수 있습니다.

print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))

산출

The MSE is: The MSE is: 5.666666666666667

예

이제 다음과 같이 값을 예측하는 데 사용하십시오.

X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))

산출

[1.]

완전한 작업 / 실행 가능 프로그램

from sklearn.datasets import load_iris

iris = load_iris()

X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))

Naïve Bayes 방법은 모든 예측 변수가 서로 독립적이라는 강력한 가정하에 Bayes의 정리를 적용하는지도 학습 알고리즘 세트입니다. 수업. 이것은 이러한 방법을 Naïve Bayes 방법이라고 부르는 순진한 가정입니다.

베이 즈 정리는 클래스의 사후 확률, 즉 레이블의 확률과 일부 관찰 된 특징을 찾기 위해 다음 관계를 설명합니다. $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$.

$$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)=\left(\frac{P\lgroup Y\rgroup P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)}{P\left(\begin{array}{c} features\end{array}\right)}\right)$$

여기, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$ 클래스의 사후 확률입니다.

$P\left(\begin{array}{c} Y\end{array}\right)$ 클래스의 사전 확률입니다.

$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ 주어진 클래스에 대한 예측 자의 확률 인 가능성입니다.

$P\left(\begin{array}{c} features\end{array}\right)$ 예측 자의 사전 확률입니다.

Scikit-learn은 Gaussian, Multinomial, Complement 및 Bernoulli와 같은 다양한 naïve Bayes 분류기 모델을 제공합니다. 그들 모두는 주로 분포에 관한 가정에 따라 다릅니다.$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ 즉, 주어진 클래스에 대한 예측 자의 확률.

Sr. 아니요	모델 및 설명
1	가우시안 나이브 베이 즈 Gaussian Naïve Bayes 분류기는 각 레이블의 데이터가 단순 가우스 분포에서 가져 온다고 가정합니다.
2	다항 나이브 베이 즈 특성이 단순 다항 분포에서 추출되었다고 가정합니다.
삼	베르누이 나이브 베이 즈 이 모델의 가정은 특성 바이너리 (0 및 1)가 본질적으로 있다는 것입니다. Bernoulli Naïve Bayes 분류의 적용은 'bag of words'모델을 사용한 텍스트 분류입니다.
4	Naïve Bayes 보완 Multinomial Bayes 분류기에 의해 만들어진 심각한 가정을 수정하도록 설계되었습니다. 이러한 종류의 NB 분류기는 불균형 데이터 세트에 적합합니다.

Naïve Bayes 분류기 빌드

Scikit-learn 데이터 세트에 Naïve Bayes 분류기를 적용 할 수도 있습니다. 아래 예에서는 GaussianNB를 적용하고 Scikit-leran의 breast_cancer 데이터 세트를 피팅합니다.

예

Import Sklearn
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
data = load_breast_cancer()
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']
   print(label_names)
   print(labels[0])
   print(feature_names[0])
   print(features[0])
train, test, train_labels, test_labels = train_test_split(
   features,labels,test_size = 0.40, random_state = 42
)
from sklearn.naive_bayes import GaussianNB
GNBclf = GaussianNB()
model = GNBclf.fit(train, train_labels)
preds = GNBclf.predict(test)
print(preds)

산출

[
   1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1
   1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 
   1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 
   1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 
   1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 
   0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 
   1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 
   1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 
   1 1 1 1 0 1 0 0 1 1 0 1
]

위의 출력은 일련의 0과 1로 구성되며, 이는 기본적으로 종양 클래스 즉 악성 및 양성에서 예측 된 값입니다.

이 장에서는 의사 결정 트리라고하는 Sklearn의 학습 방법에 대해 알아 봅니다.

Decisions tress (DT)는 가장 강력한 비모수 적지도 학습 방법입니다. 분류 및 회귀 작업에 사용할 수 있습니다. DT의 주요 목표는 데이터 특성에서 추론 된 간단한 결정 규칙을 학습하여 목표 변수 값을 예측하는 모델을 만드는 것입니다. 의사 결정 트리에는 두 가지 주요 엔티티가 있습니다. 하나는 데이터가 분할되는 루트 노드이고 다른 하나는 최종 출력을 얻은 결정 노드 또는 잎입니다.

의사 결정 트리 알고리즘

다른 의사 결정 트리 알고리즘은 아래에 설명되어 있습니다.

ID3

이 알고리즘은 1986 년 Ross Quinlan에 의해 개발되었습니다. Iterative Dichotomiser 3이라고도합니다.이 알고리즘의 주요 목표는 모든 노드에 대해 범주 형 대상에 대해 가장 큰 정보 이득을 얻을 수있는 범주 형 기능을 찾는 것입니다.

트리를 최대 크기로 키운 다음 보이지 않는 데이터에 대한 트리의 능력을 향상시키기 위해 가지 치기 단계를 적용합니다. 이 알고리즘의 출력은 다 방향 트리입니다.

C4.5

ID3의 후속 제품이며 연속 속성 값을 개별 간격 세트로 분할하는 개별 속성을 동적으로 정의합니다. 이것이 카테고리 기능의 제한을 제거한 이유입니다. 훈련 된 ID3 트리를 'IF-THEN'규칙 세트로 변환합니다.

이러한 규칙을 적용해야하는 순서를 결정하기 위해 각 규칙의 정확성을 먼저 평가합니다.

C5.0

C4.5와 유사하게 작동하지만 더 적은 메모리를 사용하고 더 작은 규칙 세트를 빌드합니다. C4.5보다 정확합니다.

카트

이를 분류 및 회귀 트리 알고리즘이라고합니다. 기본적으로 기능과 임계 값을 사용하여 이진 분할을 생성하여 각 노드에서 가장 큰 정보 이득 (Gini 인덱스라고 함)을 생성합니다.

동질성은 지니 지수에 의존하며, 지니 지수의 값이 높을수록 동질성이 높아집니다. C4.5 알고리즘과 비슷하지만 차이점은 규칙 집합을 계산하지 않고 숫자 대상 변수 (회귀)도 지원하지 않는다는 것입니다.

의사 결정 트리를 사용한 분류

이 경우 의사 결정 변수는 범주 형입니다.

Sklearn Module − Scikit-learn 라이브러리는 모듈 이름을 제공합니다. DecisionTreeClassifier 데이터 세트에 대한 다중 클래스 분류를 수행하기 위해.

매개 변수

다음 표는 sklearn.tree.DecisionTreeClassifier 모듈-

Sr. 아니요	매개 변수 및 설명
1	criterion − 문자열, 선택적 기본값 = "gini" 분할의 품질을 측정하는 기능을 나타냅니다. 지원되는 기준은 "gini"및 "entropy"입니다. 기본값은 지니 불순물을위한 지니이고 엔트로피는 정보 획득을위한 것입니다.
2	splitter − 문자열, 선택적 기본값 = "best" 각 노드에서 분할을 선택하기 위해 "최상의"또는 "무작위"중 어떤 전략을 모델에 알려줍니다.
삼	max_depth − int 또는 None, 선택 사항 default = None 이 매개 변수는 나무의 최대 깊이를 결정합니다. 기본값은 None입니다. 즉, 모든 잎이 순수 할 때까지 또는 모든 잎에 min_smaples_split 샘플보다 적을 때까지 노드가 확장됩니다.
4	min_samples_split − int, float, 선택적 기본값 = 2 이 매개 변수는 내부 노드를 분할하는 데 필요한 최소 샘플 수를 제공합니다.
5	min_samples_leaf − int, float, 선택적 기본값 = 1 이 매개 변수는 리프 노드에 있어야하는 최소 샘플 수를 제공합니다.
6	min_weight_fraction_leaf − float, 선택적 기본값 = 0. 이 매개 변수를 사용하여 모델은 리프 노드에 있어야하는 가중치 합계의 최소 가중치를 얻습니다.
7	max_features − int, float, string 또는 None, 선택 사항 default = None 최상의 분할을 찾을 때 고려할 기능의 수를 모델에 제공합니다.
8	random_state − int, RandomState 인스턴스 또는 None, 선택 사항, 기본값 = 없음 이 매개 변수는 데이터를 섞는 동안 사용되는 생성 된 의사 난수의 시드를 나타냅니다. 다음은 옵션입니다- int−이 경우 random_state 는 난수 생성기에서 사용하는 시드입니다. RandomState instance −이 경우 random_state는 난수 생성기입니다. None −이 경우 난수 생성기는 np.random에서 사용하는 RandonState 인스턴스입니다.
9	max_leaf_nodes − int 또는 None, 선택 사항 default = None 이 매개 변수는 최선의 방식으로 max_leaf_nodes를 사용하여 트리를 성장시킬 수 있습니다. 기본값은 없음이며, 이는 리프 노드 수가 무제한임을 의미합니다.
10	min_impurity_decrease − float, 선택적 기본값 = 0. 이 분할로 인해 불순물이 다음보다 크거나 같으면 모델이 노드를 분할하므로이 값은 노드 분할 기준으로 작동합니다. min_impurity_decrease value.
11	min_impurity_split − 부동, 기본값 = 1e-7 이는 나무 성장의 조기 중단을위한 임계 값을 나타냅니다.
12	class_weight − dict, dict 목록, "균형"또는 없음, 기본값 = 없음 클래스와 관련된 가중치를 나타냅니다. 형식은 {class_label : weight}입니다. 기본 옵션을 사용하면 모든 클래스의 가중치가 1이어야 함을 의미합니다. 반면에 선택하면class_weight: balanced, 자동으로 가중치를 조정하기 위해 y 값을 사용합니다.
13	presort − bool, 선택 사항 기본값 = False 피팅에서 최상의 분할을 찾는 속도를 높이기 위해 데이터를 사전 정렬할지 여부를 모델에 알려줍니다. 기본값은 false이지만 true로 설정하면 학습 프로세스가 느려질 수 있습니다.

속성

다음 표는 sklearn.tree.DecisionTreeClassifier 모듈-

Sr. 아니요	매개 변수 및 설명
1	feature_importances_ − 모양 배열 = [n_features] 이 속성은 기능 중요도를 반환합니다.
2	classes_: − 모양의 배열 = [n_classes] 또는 이러한 배열의 목록 클래스 레이블, 즉 단일 출력 문제 또는 클래스 레이블 배열 목록, 즉 다중 출력 문제를 나타냅니다.
삼	max_features_ − 정수 max_features 매개 변수의 추론 된 값을 나타냅니다.
4	n_classes_ − 정수 또는 목록 이는 클래스 수, 즉 단일 출력 문제 또는 모든 출력에 대한 클래스 수 목록 (예 : 다중 출력 문제)을 나타냅니다.
5	n_features_ − 정수 그것은 수를 준다 features fit () 메서드가 수행 될 때.
6	n_outputs_ − 정수 그것은 수를 준다 outputs fit () 메서드가 수행 될 때.

행동 양식

다음 표는 sklearn.tree.DecisionTreeClassifier 모듈-

Sr. 아니요	매개 변수 및 설명
1	apply(self, X [, check_input]) 이 메서드는 리프의 인덱스를 반환합니다.
2	decision_path(self, X [, check_input]) 이름에서 알 수 있듯이이 메서드는 트리에서 결정 경로를 반환합니다.
삼	fit(자기, X, y [, 샘플 _ 가중치,…]) fit () 메서드는 주어진 훈련 세트 (X, y)에서 결정 트리 분류기를 만듭니다.
4	get_depth(본인) 이름에서 알 수 있듯이이 메서드는 의사 결정 트리의 깊이를 반환합니다.
5	get_n_leaves(본인) 이름에서 알 수 있듯이이 메서드는 의사 결정 트리의 잎 수를 반환합니다.
6	get_params(self [, deep]) 이 방법을 사용하여 추정기에 대한 매개 변수를 얻을 수 있습니다.
7	predict(self, X [, check_input]) X의 클래스 값을 예측합니다.
8	predict_log_proba(자신, X) 우리가 제공 한 입력 샘플 X의 클래스 로그 확률을 예측합니다.
9	predict_proba(self, X [, check_input]) 우리가 제공 한 입력 샘플 X의 클래스 확률을 예측합니다.
10	score(자기, X, y [, 샘플 _ 가중치]) 이름에서 알 수 있듯이 score () 메서드는 주어진 테스트 데이터 및 레이블에 대한 평균 정확도를 반환합니다.
11	set_params(self, \ * \ * params) 이 방법으로 추정기의 매개 변수를 설정할 수 있습니다.

구현 예

아래 Python 스크립트는 sklearn.tree.DecisionTreeClassifier 25 개의 샘플과 '높이'와 '모발의 길이'라는 두 가지 특징이있는 데이터 세트에서 남성 또는 여성을 예측하기위한 분류기를 구성하는 모듈-

from sklearn import tree
from sklearn.model_selection import train_test_split
X=[[165,19],[175,32],[136,35],[174,65],[141,28],[176,15]
,[131,32],[166,6],[128,32],[179,10],[136,34],[186,2],[12
6,25],[176,28],[112,38],[169,9],[171,36],[116,25],[196,2
5], [196,38], [126,40], [197,20], [150,25], [140,32],[136,35]]
Y=['Man','Woman','Woman','Man','Woman','Man','Woman','Ma
n','Woman','Man','Woman','Man','Woman','Woman','Woman','
Man','Woman','Woman','Man', 'Woman', 'Woman', 'Man', 'Man', 'Woman', 'Woman']
data_feature_names = ['height','length of hair']
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.3, random_state = 1)
DTclf = tree.DecisionTreeClassifier()
DTclf = clf.fit(X,Y)
prediction = DTclf.predict([[135,29]])
print(prediction)

산출

['Woman']

다음과 같이 python predict_proba () 메서드를 사용하여 각 클래스의 확률을 예측할 수도 있습니다.

예

prediction = DTclf.predict_proba([[135,29]])
print(prediction)

산출

[[0. 1.]]

의사 결정 트리를 사용한 회귀

이 경우 의사 결정 변수는 연속적입니다.

Sklearn Module − Scikit-learn 라이브러리는 모듈 이름을 제공합니다. DecisionTreeRegressor 회귀 문제에 대한 의사 결정 트리를 적용합니다.

매개 변수

사용 매개 변수 DecisionTreeRegressor 에서 사용 된 것과 거의 동일합니다. DecisionTreeClassifier기준 치수. 차이점은 '기준'매개 변수에 있습니다. 에 대한DecisionTreeRegressor 모듈 ‘criterion: 문자열, 선택적 기본값 = "mse" '매개 변수는 다음 값을 갖습니다-

• mse− 평균 제곱 오차를 나타냅니다. 기능 선택 기준으로 분산 감소와 동일합니다. 각 터미널 노드의 평균을 사용하여 L2 손실을 최소화합니다.

• freidman_mse − 또한 평균 제곱 오차를 사용하지만 Friedman의 개선 점수를 사용합니다.

• mae− 평균 절대 오차를 나타냅니다. 각 터미널 노드의 중앙값을 사용하여 L1 손실을 최소화합니다.

또 다른 차이점은 ‘class_weight’ 매개 변수.

속성

의 속성 DecisionTreeRegressor 그것과 동일합니다 DecisionTreeClassifier기준 치수. 차이점은‘classes_’ 과 ‘n_classes_'속성.

행동 양식

방법 DecisionTreeRegressor 그것과 동일합니다 DecisionTreeClassifier기준 치수. 차이점은‘predict_log_proba()’ 과 ‘predict_proba()’'속성.

구현 예

의사 결정 트리 회귀 모델의 fit () 메서드는 y의 부동 소수점 값을 사용합니다. 다음을 사용하여 간단한 구현 예를 보겠습니다.Sklearn.tree.DecisionTreeRegressor −

from sklearn import tree
X = [[1, 1], [5, 5]]
y = [0.1, 1.5]
DTreg = tree.DecisionTreeRegressor()
DTreg = clf.fit(X, y)

적합하면이 회귀 모델을 사용하여 다음과 같이 예측할 수 있습니다.

DTreg.predict([[4, 5]])

산출

array([1.5])

이 장은 Sklearn의 무작위 결정 트리를 이해하는 데 도움이 될 것입니다.

무작위 의사 결정 트리 알고리즘

DT는 일반적으로 데이터를 재귀 적으로 분할하여 훈련되지만 과적 합되는 경향이 있다는 것을 알고 있기 때문에 데이터의 다양한 하위 샘플에 대해 많은 트리를 훈련하여 임의의 포리스트로 변환되었습니다. 그만큼sklearn.ensemble 모듈은 무작위 결정 트리를 기반으로 다음 두 가지 알고리즘을 가지고 있습니다-

랜덤 포레스트 알고리즘

고려중인 각 기능에 대해 로컬 최적 기능 / 분할 조합을 계산합니다. 랜덤 포레스트에서 앙상블의 각 의사 결정 트리는 훈련 세트에서 대체로 추출한 샘플에서 빌드 된 다음 각각에서 예측을 가져 와서 최종적으로 투표를 통해 최상의 솔루션을 선택합니다. 분류 및 회귀 작업 모두에 사용할 수 있습니다.

Random Forest로 분류

랜덤 포레스트 분류기를 만들기 위해 Scikit-learn 모듈은 sklearn.ensemble.RandomForestClassifier. 랜덤 포레스트 분류기를 구축하는 동안이 모듈에서 사용하는 주요 매개 변수는 다음과 같습니다.‘max_features’ 과 ‘n_estimators’.

여기, ‘max_features’노드를 분할 할 때 고려할 기능의 무작위 하위 집합 크기입니다. 이 매개 변수의 값을 none으로 선택하면 무작위 하위 집합이 아닌 모든 기능을 고려합니다. 반면에n_estimators숲에있는 나무의 수입니다. 나무 수가 많을수록 결과가 더 좋아집니다. 그러나 계산하는 데 더 오래 걸립니다.

구현 예

다음 예제에서는 다음을 사용하여 임의 포리스트 분류기를 작성합니다. sklearn.ensemble.RandomForestClassifier 또한 사용하여 정확성을 확인합니다. cross_val_score 기준 치수.

from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers = 100,random_state = 0) RFclf = RandomForestClassifier(n_estimators = 10,max_depth = None,min_samples_split = 2, random_state = 0)
scores = cross_val_score(RFclf, X, y, cv = 5)
scores.mean()

산출

0.9997

예

sklearn 데이터 셋을 사용하여 Random Forest 분류기를 만들 수도 있습니다. 다음 예에서와 같이 홍채 데이터 세트를 사용하고 있습니다. 정확도 점수와 혼동 행렬도 찾을 수 있습니다.

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score

path = "https://archive.ics.uci.edu/ml/machine-learning-database
s/iris/iris.data"
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dataset = pd.read_csv(path, names = headernames)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)
RFclf = RandomForestClassifier(n_estimators = 50)
RFclf.fit(X_train, y_train)
y_pred = RFclf.predict(X_test)
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)

산출

Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
                  precision recall f1-score support
Iris-setosa       1.00        1.00  1.00     14
Iris-versicolor   1.00        0.95  0.97     19
Iris-virginica    0.92        1.00  0.96     12

micro avg         0.98        0.98  0.98     45
macro avg         0.97        0.98  0.98     45
weighted avg      0.98        0.98  0.98     45

Accuracy: 0.9777777777777777

랜덤 포레스트를 사용한 회귀

랜덤 포레스트 회귀를 생성하기 위해 Scikit-learn 모듈은 sklearn.ensemble.RandomForestRegressor. Random Forest Regressor를 빌드하는 동안에서 사용하는 것과 동일한 매개 변수를 사용합니다.sklearn.ensemble.RandomForestClassifier.

구현 예

다음 예에서는 다음을 사용하여 임의 포리스트 회귀자를 작성합니다. sklearn.ensemble.RandomForestregressor 또한 predict () 메서드를 사용하여 새 값을 예측합니다.

from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
RFregr = RandomForestRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
RFregr.fit(X, y)

산출

RandomForestRegressor(
   bootstrap = True, criterion = 'mse', max_depth = 10,
   max_features = 'auto', max_leaf_nodes = None,
   min_impurity_decrease = 0.0, min_impurity_split = None,
   min_samples_leaf = 1, min_samples_split = 2,
   min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
   oob_score = False, random_state = 0, verbose = 0, warm_start = False
)

적합하면 다음과 같이 회귀 모델에서 예측할 수 있습니다.

print(RFregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))

산출

[98.47729198]

엑스트라 트리 방법

고려중인 각 기능에 대해 분할에 대한 임의의 값을 선택합니다. 추가 트리 방법을 사용하는 이점은 모델의 분산을 조금 더 줄일 수 있다는 것입니다. 이러한 방법을 사용할 때의 단점은 편향이 약간 증가한다는 것입니다.

Extra-Tree 방법으로 분류

Extra-tree 메서드를 사용하여 분류기를 생성하기 위해 Scikit-learn 모듈은 sklearn.ensemble.ExtraTreesClassifier. 에서 사용하는 것과 동일한 매개 변수를 사용합니다.sklearn.ensemble.RandomForestClassifier. 유일한 차이점은 위에서 설명한 방식으로 나무를 만드는 것입니다.

구현 예

다음 예제에서는 다음을 사용하여 임의 포리스트 분류기를 작성합니다. sklearn.ensemble.ExtraTreeClassifier 또한 사용하여 정확성을 확인합니다. cross_val_score 기준 치수.

from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import ExtraTreesClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers=100,random_state = 0)
ETclf = ExtraTreesClassifier(n_estimators = 10,max_depth = None,min_samples_split = 10, random_state = 0)
scores = cross_val_score(ETclf, X, y, cv = 5)
scores.mean()

산출

1.0

예

또한 sklearn 데이터 세트를 사용하여 Extra-Tree 메서드를 사용하여 분류자를 만들 수 있습니다. 다음 예에서와 같이 Pima-Indian 데이터 세트를 사용하고 있습니다.

from pandas import read_csv

from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
num_trees = 150
max_features = 5
ETclf = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)
results = cross_val_score(ETclf, X, Y, cv=kfold)
print(results.mean())

산출

0.7551435406698566

Extra-Tree 방법을 사용한 회귀

만들기 위해 Extra-Tree 회귀, Scikit-learn 모듈은 sklearn.ensemble.ExtraTreesRegressor. Random Forest Regressor를 빌드하는 동안에서 사용하는 것과 동일한 매개 변수를 사용합니다.sklearn.ensemble.ExtraTreesClassifier.

구현 예

다음 예에서는 sklearn.ensemble.ExtraTreesregressor랜덤 포레스트 회귀자를 만들 때 사용한 것과 동일한 데이터에 대해 출력의 차이를 보자

from sklearn.ensemble import ExtraTreesRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ETregr = ExtraTreesRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
ETregr.fit(X, y)

산출

ExtraTreesRegressor(bootstrap = False, criterion = 'mse', max_depth = 10,
   max_features = 'auto', max_leaf_nodes = None,
   min_impurity_decrease = 0.0, min_impurity_split = None,
   min_samples_leaf = 1, min_samples_split = 2,
   min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
   oob_score = False, random_state = 0, verbose = 0, warm_start = False)

예

적합하면 다음과 같이 회귀 모델에서 예측할 수 있습니다.

print(ETregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))

산출

[85.50955817]

이 장에서는 앙상블 모델을 구축 할 수있는 Sklearn의 부스팅 방법에 대해 알아 봅니다.

부스팅 방법은 증분 방식으로 앙상블 모델을 구축합니다. 주요 원칙은 각 기본 모델 추정기를 순차적으로 훈련하여 모델을 점진적으로 구축하는 것입니다. 강력한 앙상블을 구축하기 위해 이러한 방법은 기본적으로 학습 데이터의 여러 반복에 걸쳐 순차적으로 학습되는 몇 주 학습자를 결합합니다. sklearn.ensemble 모듈에는 다음 두 가지 부스팅 방법이 있습니다.

AdaBoost

가장 성공적인 부스팅 앙상블 방법 중 하나이며, 주요 키는 데이터 세트의 인스턴스에 가중치를 부여하는 방식입니다. 이것이 알고리즘이 후속 모델을 구성하는 동안 인스턴스에 덜주의를 기울여야하는 이유입니다.

AdaBoost를 사용한 분류

AdaBoost 분류기를 생성하기 위해 Scikit-learn 모듈은 sklearn.ensemble.AdaBoostClassifier. 이 분류기를 빌드하는 동안이 모듈에서 사용하는 주요 매개 변수는 다음과 같습니다.base_estimator. 여기서 base_estimator는base estimator부스트 된 앙상블이 만들어집니다. 이 매개 변수의 값을 없음으로 선택하면 기본 추정치는 다음과 같습니다.DecisionTreeClassifier(max_depth=1).

구현 예

다음 예제에서는 다음을 사용하여 AdaBoost 분류기를 작성합니다. sklearn.ensemble.AdaBoostClassifier 또한 점수를 예측하고 확인합니다.

from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import make_classification
X, y = make_classification(n_samples = 1000, n_features = 10,n_informative = 2, n_redundant = 0,random_state = 0, shuffle = False)
ADBclf = AdaBoostClassifier(n_estimators = 100, random_state = 0)
ADBclf.fit(X, y)

산출

AdaBoostClassifier(algorithm = 'SAMME.R', base_estimator = None,
learning_rate = 1.0, n_estimators = 100, random_state = 0)

예

적합하면 다음과 같이 새로운 값을 예측할 수 있습니다.

print(ADBclf.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))

산출

[1]

예

이제 다음과 같이 점수를 확인할 수 있습니다.

ADBclf.score(X, y)

산출

0.995

예

또한 sklearn 데이터 세트를 사용하여 Extra-Tree 메서드를 사용하여 분류자를 만들 수 있습니다. 예를 들어 아래 주어진 예에서는 Pima-Indian 데이터 세트를 사용하고 있습니다.

from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = AdaBoostClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())

산출

0.7851435406698566

AdaBoost를 사용한 회귀

Ada Boost 방법으로 회귀자를 생성하기 위해 Scikit-learn 라이브러리는 sklearn.ensemble.AdaBoostRegressor. 회귀자를 빌드하는 동안에서 사용하는 것과 동일한 매개 변수를 사용합니다.sklearn.ensemble.AdaBoostClassifier.

구현 예

다음 예에서는 다음을 사용하여 AdaBoost 회귀자를 구축하고 있습니다. sklearn.ensemble.AdaBoostregressor 또한 predict () 메서드를 사용하여 새 값을 예측합니다.

from sklearn.ensemble import AdaBoostRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ADBregr = RandomForestRegressor(random_state = 0,n_estimators = 100)
ADBregr.fit(X, y)

산출

AdaBoostRegressor(base_estimator = None, learning_rate = 1.0, loss = 'linear',
n_estimators = 100, random_state = 0)

예

적합하면 다음과 같이 회귀 모델에서 예측할 수 있습니다.

print(ADBregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))

산출

[85.50955817]

그라디언트 트리 부스팅

그것은 또한 불린다 Gradient Boosted Regression Trees(GRBT). 기본적으로 임의의 미분 손실 함수로 부스팅하는 일반화입니다. 주간 예측 모델의 앙상블 형태로 예측 모델을 생성합니다. 회귀 및 분류 문제에 사용할 수 있습니다. 이들의 주요 장점은 혼합형 데이터를 자연스럽게 처리한다는 사실입니다.

그라디언트 트리 부스트를 사용한 분류

Gradient Tree Boost 분류기를 생성하기 위해 Scikit-learn 모듈은 sklearn.ensemble.GradientBoostingClassifier. 이 분류기를 구축하는 동안이 모듈이 사용하는 주요 매개 변수는 '손실'입니다. 여기서 '손실'은 최적화 할 손실 함수의 값입니다. loss = deviance를 선택하면 확률 적 출력으로 분류하기위한 이탈도를 나타냅니다.

반면에이 매개 변수의 값을 지수로 선택하면 AdaBoost 알고리즘을 복구합니다. 매개 변수n_estimators주 학습자의 수를 제어합니다. 이름이 지정된 하이퍼 매개 변수learning_rate ((0.0, 1.0] 범위) 수축을 통한 과적 합을 제어합니다.

구현 예

다음 예에서는 다음을 사용하여 Gradient Boosting 분류기를 작성합니다. sklearn.ensemble.GradientBoostingClassifier. 이 분류기를 50 주 학습자에게 맞추고 있습니다.

from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier
X, y = make_hastie_10_2(random_state = 0)
X_train, X_test = X[:5000], X[5000:]
y_train, y_test = y[:5000], y[5000:]

GDBclf = GradientBoostingClassifier(n_estimators = 50, learning_rate = 1.0,max_depth = 1, random_state = 0).fit(X_train, y_train)
GDBclf.score(X_test, y_test)

산출

0.8724285714285714

예

sklearn 데이터 세트를 사용하여 Gradient Boosting Classifier를 사용하여 분류기를 만들 수도 있습니다. 다음 예에서와 같이 Pima-Indian 데이터 세트를 사용하고 있습니다.

from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = GradientBoostingClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())

산출

0.7946582356674234

Gradient Tree Boost를 사용한 회귀

Gradient Tree Boost 방법으로 회귀자를 생성하기 위해 Scikit-learn 라이브러리는 sklearn.ensemble.GradientBoostingRegressor. 매개 변수 이름 loss를 통해 회귀에 대한 손실 함수를 지정할 수 있습니다. 손실의 기본값은 'ls'입니다.

구현 예

다음 예에서는 다음을 사용하여 Gradient Boosting 회귀자를 구축하고 있습니다. sklearn.ensemble.GradientBoostingregressor 또한 mean_squared_error () 메서드를 사용하여 평균 제곱 오차를 찾습니다.

import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
X, y = make_friedman1(n_samples = 2000, random_state = 0, noise = 1.0)
X_train, X_test = X[:1000], X[1000:]
y_train, y_test = y[:1000], y[1000:]
GDBreg = GradientBoostingRegressor(n_estimators = 80, learning_rate=0.1,
max_depth = 1, random_state = 0, loss = 'ls').fit(X_train, y_train)

적합하면 다음과 같이 평균 제곱 오차를 찾을 수 있습니다.

mean_squared_error(y_test, GDBreg.predict(X_test))

산출

5.391246106657164

여기에서는 데이터 샘플에서 유사성을 식별하는 데 도움이되는 Sklearn의 클러스터링 방법에 대해 연구합니다.

가장 유용한 비지도 ML 방법 중 하나 인 클러스터링 방법은 데이터 샘플 간의 유사성 및 관계 패턴을 찾는 데 사용됩니다. 그 후 기능에 따라 유사성을 갖는 그룹으로 이러한 샘플을 클러스터링합니다. 클러스터링은 현재 레이블이 지정되지 않은 데이터 간의 고유 한 그룹화를 결정하므로 이것이 중요한 이유입니다.

Scikit-learn 라이브러리에는 sklearn.cluster레이블이 지정되지 않은 데이터의 클러스터링을 수행합니다. 이 모듈에서 scikit-leran에는 다음과 같은 클러스터링 방법이 있습니다.

KMeans

이 알고리즘은 중심을 계산하고 최적의 중심을 찾을 때까지 반복합니다. 클러스터 수를 지정해야하므로 이미 알려진 것으로 가정합니다. 이 알고리즘의 주요 논리는 관성이라고 알려진 기준을 최소화하여 n 개의 등분 산 그룹에서 샘플을 분리하는 데이터를 클러스터링하는 것입니다. 알고리즘에 의해 식별되는 클러스터의 수는 'K.

Scikit-learn은 sklearn.cluster.KMeansK-Means 클러스터링을 수행하는 모듈. 클러스터 중심과 관성 값을 계산하는 동안sample_weight 허용 sklearn.cluster.KMeans 일부 샘플에 더 많은 가중치를 할당하는 모듈.

선호도 전파

이 알고리즘은 수렴 할 때까지 서로 다른 샘플 쌍 사이의 '메시지 전달'개념을 기반으로합니다. 알고리즘을 실행하기 전에 클러스터 수를 지정할 필요가 없습니다. 알고리즘의 가장 큰 단점은 순서 (2)의 시간 복잡도를 가지고 있습니다.

Scikit-learn은 sklearn.cluster.AffinityPropagation 선호도 전파 클러스터링을 수행하는 모듈.

평균 이동

이 알고리즘은 주로 blobs부드러운 밀도의 샘플에서. 가장 높은 밀도의 데이터 포인트로 포인트를 이동하여 반복적으로 클러스터에 데이터 포인트를 할당합니다. 이름이 지정된 매개 변수에 의존하는 대신bandwidth 검색 할 지역의 크기를 지정하면 클러스터 수를 자동으로 설정합니다.

Scikit-learn은 sklearn.cluster.MeanShift 평균 이동 클러스터링을 수행하는 모듈.

스펙트럼 클러스터링

클러스터링 전에이 알고리즘은 기본적으로 고유 값, 즉 데이터 유사성 행렬의 스펙트럼을 사용하여 더 적은 차원에서 차원 축소를 수행합니다. 이 알고리즘의 사용은 클러스터가 많은 경우 권장되지 않습니다.

Scikit-learn은 sklearn.cluster.SpectralClustering 스펙트럼 클러스터링을 수행하는 모듈.

계층 적 클러스터링

이 알고리즘은 클러스터를 연속적으로 병합하거나 분할하여 중첩 된 클러스터를 구축합니다. 이 클러스터 계층 구조는 덴드로 그램 즉 트리로 표시됩니다. 그것은 다음 두 가지 범주에 속합니다-

Agglomerative hierarchical algorithms− 이러한 종류의 계층 적 알고리즘에서 모든 데이터 포인트는 단일 클러스터처럼 취급됩니다. 그런 다음 클러스터 쌍을 연속적으로 응집합니다. 이것은 상향식 접근 방식을 사용합니다.

Divisive hierarchical algorithms−이 계층 적 알고리즘에서 모든 데이터 포인트는 하나의 큰 클러스터로 취급됩니다. 여기에서 클러스터링 프로세스는 하향식 접근 방식을 사용하여 하나의 큰 클러스터를 다양한 작은 클러스터로 나누는 것을 포함합니다.

Scikit-learn은 sklearn.cluster.AgglomerativeClustering Agglomerative Hierarchical Clustering을 수행하기위한 모듈.

DBSCAN

그것은 “Density-based spatial clustering of applications with noise”. 이 알고리즘은 "클러스터"및 "노이즈"라는 직관적 인 개념을 기반으로합니다. 클러스터는 데이터 공간에서 밀도가 낮은 밀도 영역이며 데이터 포인트의 밀도가 낮은 영역으로 구분됩니다.

Scikit-learn은 sklearn.cluster.DBSCANDBSCAN 클러스터링을 수행하는 모듈. 이 알고리즘에서 밀도를 정의하는 데 사용되는 두 가지 중요한 매개 변수, 즉 min_samples 및 eps가 있습니다.

더 높은 매개 변수 값 min_samples 또는 eps 매개 변수 값이 낮 으면 클러스터를 형성하는 데 필요한 더 높은 밀도의 데이터 포인트에 대한 표시를 제공합니다.

광학

그것은 “Ordering points to identify the clustering structure”. 이 알고리즘은 공간 데이터에서 밀도 기반 클러스터도 찾습니다. 기본 작동 논리는 DBSCAN과 같습니다.

이는 DBSCAN 알고리즘의 주요 약점 (다양한 밀도의 데이터에서 의미있는 클러스터를 감지하는 문제)을 공간적으로 가장 가까운 지점이 순서에서 이웃이되는 방식으로 데이터베이스의 지점을 정렬하여 해결합니다.

Scikit-learn은 sklearn.cluster.OPTICS OPTICS 클러스터링을 수행하는 모듈.

버치

계층을 사용하여 균형 잡힌 반복 감소 및 클러스터링을 나타냅니다. 대규모 데이터 세트에 대해 계층 적 클러스터링을 수행하는 데 사용됩니다. 이름이 지정된 트리를 만듭니다.CFT 즉 Characteristics Feature Tree, 주어진 데이터에 대해.

CFT의 장점은 CF (특성 기능) 노드라고하는 데이터 노드가 클러스터링에 필요한 정보를 보유하고있어 전체 입력 데이터를 메모리에 보관할 필요가 없다는 것입니다.

Scikit-learn은 sklearn.cluster.Birch BIRCH 클러스터링을 수행하는 모듈.

클러스터링 알고리즘 비교

다음 표는 scikit-learn에서 클러스터링 알고리즘의 비교 (매개 변수, 확장 성 및 메트릭 기반)를 제공합니다.

Sr. 아니요	알고리즘 이름	매개 변수	확장 성	사용 된 메트릭
1	K- 평균	클러스터 수	매우 큰 n_samples	점 사이의 거리.
2	선호도 전파	제동	n_samples로는 확장 할 수 없습니다.	그래프 거리
삼	평균 이동	대역폭	n_samples로 확장 할 수 없습니다.	점 사이의 거리.
4	스펙트럼 클러스터링	클러스터 수	n_samples로 중간 수준의 확장 성. n_clusters를 사용한 작은 수준의 확장 성.	그래프 거리
5	계층 적 클러스터링	거리 임계 값 또는 클러스터 수	대형 n_samples 대형 n_ 클러스터	점 사이의 거리.
6	DBSCAN	이웃의 크기	매우 큰 n_samples 및 중간 n_clusters.	가장 가까운 지점 거리
7	광학	최소 클러스터 멤버십	매우 큰 n_sample과 큰 n_cluster.	점 사이의 거리.
8	버치	임계 값, 분기 계수	대형 n_samples 대형 n_ 클러스터	점 사이의 유클리드 거리입니다.

Scikit-learn Digit 데이터 세트의 K- 평균 클러스터링

이 예에서는 숫자 데이터 세트에 K- 평균 클러스터링을 적용합니다. 이 알고리즘은 원래 레이블 정보를 사용하지 않고 유사한 숫자를 식별합니다. 구현은 Jupyter 노트북에서 수행됩니다.

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape

산출

1797, 64)

이 출력은 숫자 데이터 세트에 64 개의 기능이있는 1797 개의 샘플이 있음을 보여줍니다.

예

이제 다음과 같이 K- 평균 클러스터링을 수행합니다.

kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape

산출

(10, 64)

이 출력은 K- 평균 클러스터링이 64 개의 기능이있는 10 개의 클러스터를 생성했음을 보여줍니다.

예

fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks = [], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)

산출

아래 출력에는 K- 평균 군집화에서 학습 한 군집 중심을 보여주는 이미지가 있습니다.

다음으로, 아래의 Python 스크립트는 학습 된 클러스터 레이블 (K-Means 기준)을 그 안에있는 실제 레이블과 일치시킵니다.

from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]

아래에 언급 된 명령을 사용하여 정확도를 확인할 수도 있습니다.

from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)

산출

0.7935447968836951

완전한 구현 예

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np

from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
   axi.set(xticks=[], yticks = [])
   axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
   mask = (clusters == i)
   labels[mask] = mode(digits.target[mask])[0]
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)

클러스터링 알고리즘의 성능을 평가할 수있는 다양한 기능이 있습니다.

다음은 클러스터링 성능을 평가하기 위해 Scikit-learn에서 제공하는 중요하고 주로 사용되는 기능입니다.

조정 된 랜드 인덱스

Rand Index는 두 군집 사이의 유사성 측정 값을 계산하는 함수입니다. 이 계산을 위해 랜드 인덱스는 예측 및 실제 클러스터링에서 유사하거나 다른 클러스터에 할당 된 모든 샘플 쌍과 계수 쌍을 고려합니다. 그 후, 원시 Rand 지수 점수는 다음 공식을 사용하여 조정 된 Rand 지수 점수로 '우연에 맞게 조정'됩니다.

$$Adjusted\:RI=\left(RI-Expected_{-}RI\right)/\left(max\left(RI\right)-Expected_{-}RI\right)$$

즉, 두 개의 매개 변수가 있습니다. labels_true, 이것은 Ground Truth 클래스 레이블입니다. labels_pred평가할 클러스터 레이블입니다.

예

from sklearn.metrics.cluster import adjusted_rand_score
   
   labels_true = [0, 0, 1, 1, 1, 1]
   labels_pred = [0, 0, 2, 2, 3, 3]

adjusted_rand_score(labels_true, labels_pred)

산출

0.4444444444444445

완벽한 라벨링은 1 점, 불량 라벨링 또는 독립적 인 라벨링은 0 점 또는 음수입니다.

상호 정보 기반 점수

상호 정보는 두 할당의 일치를 계산하는 함수입니다. 순열을 무시합니다. 사용 가능한 다음 버전이 있습니다-

NMI (Normalized Mutual Information)

Scikit가 배우다 sklearn.metrics.normalized_mutual_info_score 기준 치수.

예

from sklearn.metrics.cluster import normalized_mutual_info_score
   
   labels_true = [0, 0, 1, 1, 1, 1]
   labels_pred = [0, 0, 2, 2, 3, 3]

normalized_mutual_info_score (labels_true, labels_pred)

산출

0.7611702597222881

조정 된 상호 정보 (AMI)

Scikit가 배우다 sklearn.metrics.adjusted_mutual_info_score 기준 치수.

예

from sklearn.metrics.cluster import adjusted_mutual_info_score

   labels_true = [0, 0, 1, 1, 1, 1]
   labels_pred = [0, 0, 2, 2, 3, 3]

adjusted_mutual_info_score (labels_true, labels_pred)

산출

0.4444444444444448

Fowlkes-Mallows 점수

Fowlkes-Mallows 함수는 점 집합의 두 군집화 유사성을 측정합니다. 쌍 단위 정밀도와 재현율의 기하학적 평균으로 정의 할 수 있습니다.

수학적으로

$$FMS=\frac{TP}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)}}$$

여기, TP = True Positive − 동일한 클러스터에 속하는 포인트 쌍의 수는 모두 참 및 예측 레이블 모두입니다.

FP = False Positive − 실제 레이블에서는 동일한 클러스터에 속하지만 예측 레이블에는없는 쌍의 포인트 수.

FN = False Negative − 예측 된 레이블에서 동일한 클러스터에 속하지만 실제 레이블에는없는 쌍의 포인트 수.

Scikit 학습에는 sklearn.metrics.fowlkes_mallows_score 모듈이 있습니다.

예

from sklearn.metrics.cluster import fowlkes_mallows_score

   labels_true = [0, 0, 1, 1, 1, 1]
   labels_pred = [0, 0, 2, 2, 3, 3]

fowlkes_mallows__score (labels_true, labels_pred)

산출

0.6546536707079771

실루엣 계수

Silhouette 함수는 각 샘플에 대한 평균 군집 내 거리와 평균 가장 가까운 군집 거리를 사용하여 모든 샘플의 평균 실루엣 계수를 계산합니다.

수학적으로

$$S=\left(b-a\right)/max\left(a,b\right)$$

여기서 a는 클러스터 내 거리입니다.

b는 가장 가까운 군집 거리입니다.

Scikit은 sklearn.metrics.silhouette_score 모듈-

예

from sklearn import metrics.silhouette_score
from sklearn.metrics import pairwise_distances
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target

kmeans_model = KMeans(n_clusters = 3, random_state = 1).fit(X)
labels = kmeans_model.labels_
silhouette_score(X, labels, metric = 'euclidean')

산출

0.5528190123564091

비상 매트릭스

이 매트릭스는 모든 신뢰할 수있는 쌍 (참, 예측)에 대한 교차 카디널리티를보고합니다. 분류 문제에 대한 혼동 행렬은 정사각형 우발 행렬입니다.

Scikit은 sklearn.metrics.contingency_matrix 기준 치수.

예

from sklearn.metrics.cluster import contingency_matrix
x = ["a", "a", "a", "b", "b", "b"]
y = [1, 1, 2, 0, 1, 2]
contingency_matrix(x, y)

산출

array([
   [0, 2, 1],
   [1, 1, 1]
])

위 출력의 첫 번째 행은 실제 군집이 "a"인 3 개의 샘플 중 0에있는 샘플이 하나도없고, 그 중 2 개는 1에 있고 1은 2에 있음을 보여줍니다. 반면에 두 번째 행은 3 개의 샘플 중 실제 클러스터는 "b"이고 1은 0, 1은 1, 1은 2입니다.

차원 축소, 비지도 머신 러닝 방법은 주요 특징 세트를 선택하는 각 데이터 샘플에 대한 특징 변수의 수를 줄이는 데 사용됩니다. PCA (Principal Component Analysis)는 차원 감소를위한 널리 사용되는 알고리즘 중 하나입니다.

정확한 PCA

Principal Component Analysis (PCA)는 다음을 사용하여 선형 차원 감소에 사용됩니다. Singular Value Decomposition(SVD) 데이터를 더 낮은 차원의 공간에 투영합니다. PCA를 사용하여 분해하는 동안 입력 데이터는 중앙에 있지만 SVD를 적용하기 전에 각 기능에 대해 스케일링되지 않습니다.

Scikit-learn ML 라이브러리는 sklearn.decomposition.PCAfit () 메서드에서 n 개의 구성 요소를 학습하는 변환기 객체로 구현 된 모듈입니다. 또한 새 데이터에서 이러한 구성 요소에 투영하는 데 사용할 수도 있습니다.

예

아래 예제는 sklearn.decomposition.PCA 모듈을 사용하여 Pima Indians Diabetes 데이터 세트에서 가장 좋은 5 가지 주요 구성 요소를 찾습니다.

from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', ‘class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 5)
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)

산출

Explained Variance: [0.88854663 0.06159078 0.02579012 0.01308614 0.00744094]
[
   [-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
   [-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
   [-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
   [-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
   [ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
]

증분 PCA

Incremental Principal Component Analysis (IPCA)는 PCA (Principal Component Analysis)의 가장 큰 한계를 해결하는 데 사용되며 PCA는 배치 처리 만 지원하므로 처리 할 모든 입력 데이터가 메모리에 맞아야합니다.

Scikit-learn ML 라이브러리는 sklearn.decomposition.IPCA Out-of-Core PCA를 구현할 수 있도록하는 모듈 partial_fit 순차적으로 가져온 데이터 청크에 대한 방법을 사용하거나 np.memmap, 전체 파일을 메모리로로드하지 않고 메모리 매핑 된 파일입니다.

PCA와 동일하지만 IPCA를 사용하여 분해하는 동안 입력 데이터는 중앙에 배치되지만 SVD를 적용하기 전에 각 기능에 대해 스케일링되지 않습니다.

예

아래 예제는 sklearn.decomposition.IPCA Sklearn 숫자 데이터 세트의 모듈.

from sklearn.datasets import load_digits
from sklearn.decomposition import IncrementalPCA
X, _ = load_digits(return_X_y = True)
transformer = IncrementalPCA(n_components = 10, batch_size = 100)
transformer.partial_fit(X[:100, :])
X_transformed = transformer.fit_transform(X)
X_transformed.shape

산출

(1797, 10)

여기서는 소규모 데이터 배치에 부분적으로 맞출 수 있습니다 (배치 당 100 개에서했던 것처럼). fit() 데이터를 배치로 나누는 기능.

커널 PCA

PCA의 확장 인 Kernel Principal Component Analysis는 커널을 사용하여 비선형 차원 감소를 달성합니다. 그것은 둘 다 지원합니다transform and inverse_transform.

Scikit-learn ML 라이브러리는 sklearn.decomposition.KernelPCA 기준 치수.

예

아래 예제는 sklearn.decomposition.KernelPCASklearn 숫자 데이터 세트의 모듈. 시그 모이 드 커널을 사용하고 있습니다.

from sklearn.datasets import load_digits
from sklearn.decomposition import KernelPCA
X, _ = load_digits(return_X_y = True)
transformer = KernelPCA(n_components = 10, kernel = 'sigmoid')
X_transformed = transformer.fit_transform(X)
X_transformed.shape

산출

(1797, 10)

무작위 SVD를 사용하는 PCA

무작위 SVD를 사용하는 주성분 분석 (PCA)은 낮은 특이 값과 관련된 성분의 특이 벡터를 삭제하여 대부분의 분산을 유지하면서 데이터를 낮은 차원 공간에 투영하는 데 사용됩니다. 여기,sklearn.decomposition.PCA 선택적 매개 변수가있는 모듈 svd_solver=’randomized’ 매우 유용 할 것입니다.

예

아래 예제는 sklearn.decomposition.PCA 선택적 매개 변수 svd_solver = 'randomized'가있는 모듈을 사용하여 Pima Indians Diabetes 데이터 세트에서 가장 좋은 7 가지 주요 구성 요소를 찾습니다.

from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 7,svd_solver = 'randomized')
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)

산출

Explained Variance: [8.88546635e-01 6.15907837e-02 2.57901189e-02 1.30861374e-027.44093864e-03 3.02614919e-03 5.12444875e-04]
[
   [-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
   [-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
   [-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
   [-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
   [ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
   [-5.04730888e-03 5.07391813e-02 7.56365525e-02 2.21363068e-01-6.13326472e-03 -9.70776708e-01 -2.02903702e-03 -1.51133239e-02]
   [ 9.86672995e-01 8.83426114e-04 -1.22975947e-03 -3.76444746e-041.42307394e-03 -2.73046214e-03 -6.34402965e-03 -1.62555343e-01]
]