Scikit Learn-서포트 벡터 머신

이 장에서는 SVM (Support Vector Machine)이라는 기계 학습 방법을 다룹니다.

소개

SVM (Support Vector Machine)은 분류, 회귀 및 이상 값 감지에 사용되는 강력하면서도 유연한 감독 형 기계 학습 방법입니다. SVM은 고차원 공간에서 매우 효율적이며 일반적으로 분류 문제에 사용됩니다. SVM은 의사 결정 기능에서 훈련 포인트의 하위 집합을 사용하기 때문에 인기 있고 메모리 효율적입니다.

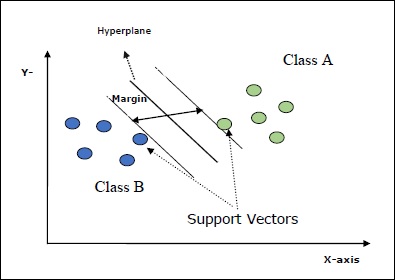
SVM의 주요 목표는 데이터 세트를 여러 클래스로 나누는 것입니다. maximum marginal hyperplane (MMH) 다음 두 단계로 수행 할 수 있습니다.

Support Vector Machines는 먼저 클래스를 최상의 방법으로 분리하는 초평면을 반복적으로 생성합니다.
그 후 클래스를 올바르게 분리하는 초평면을 선택합니다.

SVM의 몇 가지 중요한 개념은 다음과 같습니다.

Support Vectors− 초평면에 가장 가까운 데이터 포인트로 정의 할 수 있습니다. 지원 벡터는 구분선을 결정하는 데 도움이됩니다.
Hyperplane − 서로 다른 클래스를 가진 개체 집합을 나누는 결정 평면 또는 공간.
Margin − 서로 다른 클래스의 옷장 데이터 포인트에서 두 줄 사이의 간격을 여백이라고합니다.

다음 다이어그램은 이러한 SVM 개념에 대한 통찰력을 제공합니다.

Scikit-learn의 SVM은 희소 및 조밀 샘플 벡터를 입력으로 모두 지원합니다.

SVM 분류

Scikit-learn은 세 가지 클래스를 제공합니다. SVC, NuSVC 과 LinearSVC 다중 클래스 클래스 분류를 수행 할 수 있습니다.

SVC

구현이 기반으로하는 C 지원 벡터 분류입니다. libsvm. scikit-learn에서 사용하는 모듈은 다음과 같습니다.sklearn.svm.SVC. 이 클래스는 일대일 체계에 따라 다중 클래스 지원을 처리합니다.

매개 변수

다음 표는에서 사용하는 매개 변수로 구성됩니다. sklearn.svm.SVC 클래스-

Sr. 아니요	매개 변수 및 설명
1	C − 부동, 선택, 기본값 = 1.0 오류 항의 페널티 매개 변수입니다.
2	kernel − 문자열, 선택 사항, 기본값 = 'rbf' 이 매개 변수는 알고리즘에서 사용할 커널 유형을 지정합니다. 다음 중 하나를 선택할 수 있습니다.‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. 커널의 기본값은 다음과 같습니다.‘rbf’.
삼	degree − int, 선택, 기본값 = 3 '다중'커널 기능의 정도를 나타내며 다른 모든 커널에서는 무시됩니다.
4	gamma − { 'scale', 'auto'} 또는 float, 커널 'rbf', 'poly'및 'sigmoid'에 대한 커널 계수입니다.
5	optinal default − = '스케일' 기본값, 즉 gamma = 'scale'을 선택하면 SVC에서 사용할 감마 값은 1 / (_ ∗. ())입니다. 반면 gamma = 'auto'이면 1 / _를 사용합니다.
6	coef0 − 부동, 선택, 기본값 = 0.0 'poly'와 'sigmoid'에서만 중요한 커널 함수의 독립 용어입니다.
7	tol − 부동, 선택, 기본값 = 1.e-3 이 매개 변수는 반복의 중지 기준을 나타냅니다.
8	shrinking − 부울, 옵션, 기본값 = True 이 매개 변수는 축소 휴리스틱 사용 여부를 나타냅니다.
9	verbose − 부울, 기본값 : false 자세한 출력을 활성화하거나 비활성화합니다. 기본값은 false입니다.
10	probability − 부울, 옵션, 기본값 = true 이 매개 변수는 확률 추정을 활성화하거나 비활성화합니다. 기본값은 false이지만 fit을 호출하기 전에 활성화해야합니다.
11	max_iter − int, 선택, 기본값 = -1 이름에서 알 수 있듯이 솔버 내의 최대 반복 횟수를 나타냅니다. 값 -1은 반복 횟수에 제한이 없음을 의미합니다.
12	cache_size − 부동, 선택 사항 이 매개 변수는 커널 캐시의 크기를 지정합니다. 값은 MB (MegaBytes) 단위입니다.
13	random_state − int, RandomState 인스턴스 또는 None, 선택 사항, 기본값 = 없음 이 매개 변수는 데이터를 섞는 동안 사용되는 생성 된 의사 난수의 시드를 나타냅니다. 다음은 옵션입니다- int−이 경우 random_state 는 난수 생성기에서 사용하는 시드입니다. RandomState instance −이 경우 random_state는 난수 생성기입니다. None −이 경우 난수 생성기는 np.random에서 사용하는 RandonState 인스턴스입니다.
14	class_weight − {dict, 'balanced'}, 선택 사항 이 매개 변수는 SVC에 대해 클래스 j의 매개 변수 C를 _ℎ [] ∗로 설정합니다. 기본 옵션을 사용하면 모든 클래스의 가중치가 1이어야 함을 의미합니다. 반면에 선택하면*class_weight:balanced*, 자동으로 가중치를 조정하기 위해 y 값을 사용합니다.
15	decision_function_shape − ovo ','ovr ', 기본값 ='ovr ' 이 매개 변수는 알고리즘이 ‘ovr’ (one-vs-rest) 다른 모든 분류기와 같은 모양의 결정 함수 또는 원본 ovo(one-vs-one) libsvm의 결정 기능.
16	break_ties − 부울, 옵션, 기본값 = false True − 예측은 decision_function의 신뢰도 값에 따라 동점을 끊습니다. False − 예측은 동점 클래스 중 첫 번째 클래스를 반환합니다.

속성

다음 표는에서 사용하는 속성으로 구성됩니다. sklearn.svm.SVC 클래스-

Sr. 아니요	속성 및 설명
1	support_ − 배열 형, 모양 = [n_SV] 지원 벡터의 인덱스를 반환합니다.
2	support_vectors_ − 배열 형, 모양 = [n_SV, n_features] 지원 벡터를 반환합니다.
삼	n_support_ − 배열 형, dtype = int32, 모양 = [n_class] 각 클래스에 대한 지원 벡터의 수를 나타냅니다.
4	dual_coef_ − 배열, 모양 = [n_class-1, n_SV] 이것은 결정 함수에서 지원 벡터의 계수입니다.
5	coef_ − 배열, 모양 = [n_class * (n_class-1) / 2, n_features] 이 속성은 선형 커널의 경우에만 사용할 수 있으며 기능에 할당 된 가중치를 제공합니다.
6	intercept_ − 배열, 모양 = [n_class * (n_class-1) / 2] 의사 결정 기능에서 독립적 인 용어 (상수)를 나타냅니다.
7	fit_status_ − 정수 올바르게 장착 된 경우 출력은 0이됩니다. 잘못 장착 된 경우 출력은 1이됩니다.
8	classes_ − 모양 배열 = [n_classes] 클래스의 레이블을 제공합니다.

Implementation Example

다른 분류기와 마찬가지로 SVC도 다음 두 배열에 적합해야합니다.

배열 X훈련 샘플을 들고. 크기는 [n_samples, n_features]입니다.
배열 Y목표 값, 즉 훈련 샘플에 대한 클래스 레이블을 보유합니다. 크기는 [n_samples]입니다.

다음 Python 스크립트 사용 sklearn.svm.SVC 클래스-

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)

Output

SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, probability = False, random_state = None, shrinking = False,
   tol = 0.001, verbose = False)

Example

이제 적합하면 다음 파이썬 스크립트의 도움으로 가중치 벡터를 얻을 수 있습니다.

SVCClf.coef_

Output

array([[0.5, 0.5]])

Example

마찬가지로 다음과 같이 다른 속성의 값을 얻을 수 있습니다.

SVCClf.predict([[-0.5,-0.8]])

Output

array([1])

Example

SVCClf.n_support_

Output

array([1, 1])

Example

SVCClf.support_vectors_

Output

array(
   [
      [-1., -1.],
      [ 1., 1.]
   ]
)

Example

SVCClf.support_

Output

array([0, 2])

Example

SVCClf.intercept_

Output

array([-0.])

Example

SVCClf.fit_status_

Output

NuSVC

NuSVC는 Nu 지원 벡터 분류입니다. 다중 클래스 분류를 수행 할 수있는 scikit-learn에서 제공하는 또 다른 클래스입니다. SVC와 비슷하지만 NuSVC는 약간 다른 매개 변수 집합을 허용합니다. SVC와 다른 매개 변수는 다음과 같습니다.

nu − 부동, 선택, 기본값 = 0.5

훈련 오류 비율의 상한과 지원 벡터 비율의 하한을 나타냅니다. 값은 (o, 1] 간격에 있어야합니다.

나머지 매개 변수 및 속성은 SVC와 동일합니다.

구현 예

다음을 사용하여 동일한 예제를 구현할 수 있습니다. sklearn.svm.NuSVC 수업도.

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)

산출

NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, nu = 0.5, probability = False, random_state = None,
   shrinking = False, tol = 0.001, verbose = False)

SVC의 경우처럼 나머지 속성의 출력을 얻을 수 있습니다.

LinearSVC

선형 지원 벡터 분류입니다. 커널 = '선형'인 SVC와 유사합니다. 그들 사이의 차이점은LinearSVC liblinear 측면에서 구현되는 동안 SVC는 libsvm. 그게 이유야LinearSVC페널티 및 손실 기능을 더 유연하게 선택할 수 있습니다. 또한 많은 수의 샘플로 더 잘 확장됩니다.

매개 변수와 속성에 대해 이야기하면 지원하지 않습니다. ‘kernel’ 선형이라고 가정하고 다음과 같은 속성이 부족하기 때문입니다. support_, support_vectors_, n_support_, fit_status_ 과, dual_coef_.

그러나 penalty 과 loss 다음과 같이 매개 변수-

penalty − string, L1 or L2(default = ‘L2’)

이 매개 변수는 벌점 (정규화)에 사용되는 표준 (L1 또는 L2)을 지정하는 데 사용됩니다.
loss − string, hinge, squared_hinge (default = squared_hinge)

'hinge'가 표준 SVM 손실이고 'squared_hinge'가 힌지 손실의 제곱 인 손실 함수를 나타냅니다.

구현 예

다음 Python 스크립트 사용 sklearn.svm.LinearSVC 클래스-

from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)

산출

LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
   intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
   multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)

예

이제 적합하면 모델은 다음과 같이 새로운 값을 예측할 수 있습니다.

LSVCClf.predict([[0,0,0,0]])

산출

[1]

예

위의 예에서 다음 파이썬 스크립트를 사용하여 가중치 벡터를 얻을 수 있습니다.

LSVCClf.coef_

산출

[[0. 0. 0.91214955 0.22630686]]

예

유사하게, 우리는 다음 파이썬 스크립트의 도움으로 intercept의 값을 얻을 수 있습니다.

LSVCClf.intercept_

산출

[0.26860518]

SVM을 사용한 회귀

앞서 논의했듯이 SVM은 분류 및 회귀 문제 모두에 사용됩니다. Scikit-learn의 SVC (Support Vector Classification) 방법을 확장하여 회귀 문제를 해결할 수도 있습니다. 확장 된 방법을 SVR (Support Vector Regression)이라고합니다.

SVM과 SVR의 기본적인 유사성

SVC에 의해 생성 된 모델은 훈련 데이터의 하위 집합에만 의존합니다. 왜? 모델 구축을위한 비용 함수는 마진 밖에있는 훈련 데이터 포인트에 대해 신경 쓰지 않기 때문입니다.

반면 SVR (Support Vector Regression)에 의해 생성 된 모델은 훈련 데이터의 하위 집합에만 의존합니다. 왜? 모델 구축을위한 비용 함수는 모델 예측에 가까운 모든 학습 데이터 포인트를 무시하기 때문입니다.

Scikit-learn은 세 가지 클래스를 제공합니다. SVR, NuSVR and LinearSVR SVR의 세 가지 구현으로.

SVR

구현이 기반으로하는 Epsilon 지원 벡터 회귀입니다. libsvm. 반대로SVC 모델에는 두 개의 자유 매개 변수가 있습니다. ‘C’ 과 ‘epsilon’.

epsilon − 부동, 선택, 기본값 = 0.1

엡실론 -SVR 모델의 엡실론을 나타내며, 실제 값에서 엡실론 거리 내에서 예측 된 포인트로 훈련 손실 함수에서 페널티가없는 엡실론 튜브를 지정합니다.

나머지 매개 변수와 속성은 우리가 사용한 것과 유사합니다. SVC.

구현 예

다음 Python 스크립트 사용 sklearn.svm.SVR 클래스-

from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)

산출

SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
   kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)

예

이제 적합하면 다음 파이썬 스크립트의 도움으로 가중치 벡터를 얻을 수 있습니다.

SVRReg.coef_

산출

array([[0.4, 0.4]])

예

마찬가지로 다음과 같이 다른 속성의 값을 얻을 수 있습니다.

SVRReg.predict([[1,1]])

산출

array([1.1])

마찬가지로 다른 속성의 값도 가져올 수 있습니다.

NuSVR

NuSVR은 Nu 지원 벡터 회귀입니다. NuSVC와 비슷하지만 NuSVR은 매개 변수를 사용합니다.nu지원 벡터의 수를 제어합니다. 또한 NuSVC와 달리nu C 매개 변수를 대체했습니다. 여기서는 epsilon.

구현 예

다음 Python 스크립트 사용 sklearn.svm.SVR 클래스-

from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)

산출

NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
   kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
   verbose = False)

예

이제 적합하면 다음 파이썬 스크립트의 도움으로 가중치 벡터를 얻을 수 있습니다.

NuSVRReg.coef_

산출

array(
   [
      [-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
      0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
      -0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
   ]
)

마찬가지로 다른 속성의 값도 얻을 수 있습니다.

LinearSVR

선형 지원 벡터 회귀입니다. 커널 = 'linear'인 SVR과 유사합니다. 그들 사이의 차이점은LinearSVR 측면에서 구현 liblinear, SVC는 libsvm. 그게 이유야LinearSVR페널티 및 손실 기능을 더 유연하게 선택할 수 있습니다. 또한 많은 수의 샘플로 더 잘 확장됩니다.

그러나 다음과 같이 '손실'매개 변수를 지원합니다.

loss − 문자열, 선택 사항, 기본값 = 'epsilon_insensitive'

epsilon_insensitive loss가 L1 손실이고 제곱 된 epsilon-insensitive loss가 L2 손실 인 손실 함수를 나타냅니다.

구현 예

다음 Python 스크립트 사용 sklearn.svm.LinearSVR 클래스-

from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)

산출

LinearSVR(
   C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
   intercept_scaling=1.0, loss='squared_epsilon_insensitive',
   max_iter=1000, random_state=0, tol=1e-05, verbose=0
)

예

이제 적합하면 모델은 다음과 같이 새로운 값을 예측할 수 있습니다.

LSRReg.predict([[0,0,0,0]])

산출

array([-0.01041416])

예

위의 예에서 다음 파이썬 스크립트를 사용하여 가중치 벡터를 얻을 수 있습니다.

LSRReg.coef_

산출

array([20.47354746, 34.08619401, 67.23189022, 87.47017787])

예

유사하게, 우리는 다음 파이썬 스크립트의 도움으로 intercept의 값을 얻을 수 있습니다.

LSRReg.intercept_

산출

array([-0.01041416])